RL 实践(6)—— CartPole【REINFORCE with baseline A2C】
- 本文介绍 REINFORCE with baseline 和 A2C 这两个带 baseline 的策略梯度方法,并在 CartPole-V0 上验证它们和无 baseline 的原始方法 REINFORCE & Actor-Critic 的优势
- 参考:《动手学强化学习》
- 完整代码下载:7_[Gym] CartPole-V0 (REINFORCE with baseline and A2C)
文章目录
- 1. CartPole-V0 环境
- 2. Policy Gradient with Baseline
- 2.1 带 baseline 的策略梯度定理
- 2.2 REINFORCE with baseline
- 2.2.1 伪代码
- 2.2.2 用 REINFORCE with baseline 方法解决 CartPole 问题
- 2.2.3 性能
- 2.3 Advantage Actor-Critic (A2C)
- 2.3.1 伪代码
- 2.3.2 用 A2C 方法解决 CartPole 问题
- 2.3.3 性能
- 2.3.4 引入目标网络
- 3. 总结
1. CartPole-V0 环境
-
本次实验使用 gym 自带的 CartPole-V0 环境。这是一个经典的一阶倒立摆控制问题,agent 的任务是通过左右移动保持车上的杆竖直,若杆的倾斜度数过大,或者车子离初始位置左右的偏离程度过大,或者坚持时间到达 200 帧,则游戏结束

-
此环境的状态空间为
维度 意义 取值范围 0 滚球 x 轴坐标 [ 0 , width ] [0,\space \text{width}] [0, width] 1 滚球 y 轴坐标 [ − inf , inf ] [-\inf, \space \inf] [−inf, inf] 2 滚球 x 轴速度 [ − 41.8 ° , 41.8 ° ] [-41.8°,\space ~ 41.8°] [−41.8°, 41.8°] 3 滚球 y 轴速度 [ − inf , inf ] [-\inf, \space \inf] [−inf, inf] 动作空间为
维度 意义 0 向左移动小车 1 向右移动小车 奖励函数为每个 timestep 得到 1 的奖励,agent 坚持时间越长,则最后的分数越高,坚持 200 帧即可获得最高的分数 200
倒立摆问题传统上可以用 pid 方法良好地解决。如果对 PID 这一套感兴趣,可以参考我的视频
- 一看就懂的pid控制理论入门
- 倒立摆模拟器
-
下面给出环境的测试代码
import os import sys import gym base_path = os.path.abspath(os.path.join(os.path.dirname(__file__), '..')) sys.path.append(base_path)import time from gym.utils.env_checker import check_envenv_name = 'CartPole-v0' env = gym.make(env_name, render_mode='human') check_env(env.unwrapped) # 检查环境是否符合 gym 规范 env.action_space.seed(10) observation, _ = env.reset(seed=10)# 测试环境 for i in range(100):while True:action = env.action_space.sample()state, reward, terminated, truncated, _ = env.step(action)if terminated or truncated:env.reset()breaktime.sleep(0.01)env.render()# 关闭环境渲染 env.close()
2. Policy Gradient with Baseline
- 上文 RL 实践(5)—— 二维滚球环境【REINFORCE & Actor-Critic】 介绍了两种经典的 Policy-Gradient 方法,Actor-Critic 和 REINFORCE,本文介绍这两种方法通用的一个改进技巧,可以有效提高算法的性能,并减小方差。
- 首先回顾一下策略梯度方法的基本原理:对于用参数 θ \theta θ 形式化的策略网络 π θ : S → A \pi_\theta:\mathcal{S}\to\mathcal{A} πθ:S→A,策略学习可以转换为如下优化问题
max θ { J ( θ ) = △ E s [ V π θ ( s ) ] } \max_\theta \left\{J(\theta) \stackrel{\triangle}{=} \mathbb{E}_s[V_{\pi_\theta}(s)] \right\} θmax{J(θ)=△Es[Vπθ(s)]} 这个优化问题可以用梯度上升来解
θ ← θ + β ⋅ ▽ θ J ( θ ) \theta \leftarrow \theta + \beta ·\triangledown_{\theta}J(\theta) θ←θ+β⋅▽θJ(θ) 其中策略梯度可以用策略梯度定理计算
▽ θ J ( θ ) ∝ E S ∼ d ( ⋅ ) [ E A ∼ π θ ( ⋅ ∣ S ) [ ▽ θ ln π θ ( A ∣ S ) ⋅ Q π θ ( S , A ) ] ] \triangledown_{\theta}J(\theta)\propto \mathbb{E}_{S \sim d(\cdot)}\Big[\mathbb{E}_{A \sim \pi_\theta(\cdot \mid S)}\left[\triangledown_{\theta}\ln \pi_\theta(A \mid S) \cdot Q_{\pi_\theta}(S, A)\right]\Big] ▽θJ(θ)∝ES∼d(⋅)[EA∼πθ(⋅∣S)[▽θlnπθ(A∣S)⋅Qπθ(S,A)]] 我们通过两次 MC 近似消去两个积分,得到随机策略梯度
g θ ( s , a ) = △ ▽ θ ln π θ ( a ∣ s ) ⋅ Q π θ ( s , a ) g_\theta(s,a) \stackrel{\triangle}{=} \triangledown_{\theta}\ln \pi_\theta(a|s) \cdot Q_{\pi_\theta}(s,a) gθ(s,a)=△▽θlnπθ(a∣s)⋅Qπθ(s,a) 其中 s , a s,a s,a 来自策略 π θ \pi_\theta πθ 和环境环境的某个具体 transition。最后,对动作价值函数 Q π ( s , a ) Q_\pi(s, a) Qπ(s,a) 的两种近似方案引出了两种策略梯度方法:REINFORCE:用实际 return u u u MC 近似 Q π ( s , a ) Q_\pi(s, a) Qπ(s,a)Actor-Critic:用神经网络(Critic) q w ( s , a ) q_w(s, a) qw(s,a) 近似 Q π ( s , a ) Q_\pi(s, a) Qπ(s,a)
2.1 带 baseline 的策略梯度定理
- 我们首先证明一个引理:设 b b b 是任意函数, b b b 不依赖于 A A A。那么对于任意的 s s s,有
E A ∼ π θ ( ⋅ ∣ s ) [ b ⋅ ▽ θ ln π θ ( A ∣ s ) ] = 0 \mathbb{E}_{A \sim \pi_{\boldsymbol{\theta}}(\cdot \mid s )}\left[b \cdot \triangledown_{\theta}\ln \pi_\theta(A \mid s)\right]=0 EA∼πθ(⋅∣s)[b⋅▽θlnπθ(A∣s)]=0由于 b b b 不依赖于动作 A A A,首先把 b b b 提取到期望外面
E A ∼ π ( ⋅ ∣ s ; θ ) [ b ⋅ ∂ ln π ( A ∣ s ; θ ) ∂ θ ] = b ⋅ E A ∼ π ( ⋅ ∣ s ; θ ) [ ∂ ln π ( A ∣ s ; θ ) ∂ θ ] = b ⋅ ∑ a ∈ A π ( a ∣ s ; θ ) ⋅ ∂ ln π ( a ∣ s ; θ ) ∂ θ = b ⋅ ∑ a ∈ A π ( a ∣ s ; θ ) ⋅ 1 π ( a ∣ s ; θ ) ⋅ ∂ π ( a ∣ s ; θ ) ∂ θ = b ⋅ ∑ a ∈ A ∂ π ( a ∣ s ; θ ) ∂ θ \begin{aligned} \mathbb{E}_{A \sim \pi(\cdot \mid s ; \boldsymbol{\theta})}\left[b \cdot \frac{\partial \ln \pi(A \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\right] & =b \cdot \mathbb{E}_{A \sim \pi(\cdot \mid s ; \boldsymbol{\theta})}\left[\frac{\partial \ln \pi(A \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\right] \\ & =b \cdot \sum_{a \in \mathcal{A}} \pi(a \mid s ; \boldsymbol{\theta}) \cdot \frac{\partial \ln \pi(a \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \\ & =b \cdot \sum_{a \in \mathcal{A}} \pi(a \mid s ; \boldsymbol{\theta}) \cdot \frac{1}{\pi(a \mid s ; \boldsymbol{\theta})} \cdot \frac{\partial \pi(a \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \\ & =b \cdot \sum_{a \in \mathcal{A}} \frac{\partial \pi(a \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \end{aligned} EA∼π(⋅∣s;θ)[b⋅∂θ∂lnπ(A∣s;θ)]=b⋅EA∼π(⋅∣s;θ)[∂θ∂lnπ(A∣s;θ)]=b⋅a∈A∑π(a∣s;θ)⋅∂θ∂lnπ(a∣s;θ)=b⋅a∈A∑π(a∣s;θ)⋅π(a∣s;θ)1⋅∂θ∂π(a∣s;θ)=b⋅a∈A∑∂θ∂π(a∣s;θ) 上式最右边的连加是关于 a a a 求的,而偏导是关于 θ \theta θ 求的,因此可以把连加放入偏导内部
E A ∼ π ( ⋅ ∣ s ; θ ) [ b ⋅ ∂ ln π ( A ∣ s ; θ ) ∂ θ ] = b ⋅ ∂ ∂ θ ∑ a ∈ A π ( a ∣ s ; θ ) ⏟ 恒等于 1 . = b ⋅ ∂ 1 ∂ θ = 0. \begin{aligned} \mathbb{E}_{A \sim \pi(\cdot \mid s ; \boldsymbol{\theta})}\left[b \cdot \frac{\partial \ln \pi(A \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\right]&=b \cdot \frac{\partial}{\partial \boldsymbol{\theta}} \underbrace{\sum_{a \in \mathcal{A}} \pi(a \mid s ; \boldsymbol{\theta})}_{\text {恒等于 } 1} . \\ &=b \cdot \frac{\partial 1}{\partial \boldsymbol{\theta}}=0 . \end{aligned} EA∼π(⋅∣s;θ)[b⋅∂θ∂lnπ(A∣s;θ)]=b⋅∂θ∂恒等于 1 a∈A∑π(a∣s;θ).=b⋅∂θ∂1=0. - 证明此引理后,我们可以把这一项引入到策略梯度定义给出的策略梯度中
▽ θ J ( θ ) ∝ E S ∼ d ( ⋅ ) [ E A ∼ π θ ( ⋅ ∣ S ) [ ▽ θ ln π θ ( A ∣ S ) ⋅ Q π θ ( S , A ) ] ] = E S ∼ d ( ⋅ ) [ E A ∼ π θ ( ⋅ ∣ S ) [ ▽ θ ln π θ ( A ∣ S ) ⋅ Q π θ ( S , A ) ] − 0 ] = E S ∼ d ( ⋅ ) [ E A ∼ π θ ( ⋅ ∣ S ) [ ▽ θ ln π θ ( A ∣ S ) ⋅ Q π θ ( S , A ) ] − E A ∼ π θ ( ⋅ ∣ s ) [ b ⋅ ▽ θ ln π θ ( A ∣ s ) ] ] = E S ∼ d ( ⋅ ) [ E A ∼ π θ ( ⋅ ∣ S ) [ ▽ θ ln π θ ( A ∣ S ) ⋅ ( Q π θ ( S , A ) − b ) ] ] \begin{aligned} \triangledown_{\theta}J(\theta) &\propto \mathbb{E}_{S \sim d(\cdot)}\Big[\mathbb{E}_{A \sim \pi_\theta(\cdot \mid S)}\left[\triangledown_{\theta}\ln \pi_\theta(A \mid S) \cdot Q_{\pi_\theta}(S, A)\right]\Big] \\ &= \mathbb{E}_{S \sim d(\cdot)}\Big[\mathbb{E}_{A \sim \pi_\theta(\cdot \mid S)}\left[\triangledown_{\theta}\ln \pi_\theta(A \mid S) \cdot Q_{\pi_\theta}(S, A)\right]-0\Big] \\ &= \mathbb{E}_{S \sim d(\cdot)}\Big[\mathbb{E}_{A \sim \pi_\theta(\cdot \mid S)}\left[\triangledown_{\theta}\ln \pi_\theta(A \mid S) \cdot Q_{\pi_\theta}(S, A)\right]-\mathbb{E}_{A \sim \pi_{\boldsymbol{\theta}}(\cdot \mid s )}\left[b \cdot \triangledown_{\theta}\ln \pi_\theta(A \mid s)\right]\Big] \\ &= \mathbb{E}_{S \sim d(\cdot)}\Big[\mathbb{E}_{A \sim \pi_\theta(\cdot \mid S)}\left[\triangledown_{\theta}\ln \pi_\theta(A \mid S) \cdot \big(Q_{\pi_\theta}(S, A)-b\big)\right]\Big] \\ \end{aligned} ▽θJ(θ)∝ES∼d(⋅)[EA∼πθ(⋅∣S)[▽θlnπθ(A∣S)⋅Qπθ(S,A)]]=ES∼d(⋅)[EA∼πθ(⋅∣S)[▽θlnπθ(A∣S)⋅Qπθ(S,A)]−0]=ES∼d(⋅)[EA∼πθ(⋅∣S)[▽θlnπθ(A∣S)⋅Qπθ(S,A)]−EA∼πθ(⋅∣s)[b⋅▽θlnπθ(A∣s)]]=ES∼d(⋅)[EA∼πθ(⋅∣S)[▽θlnπθ(A∣S)⋅(Qπθ(S,A)−b)]] 进而可以得到带基线的随机策略梯度,它仍是对原策略梯度的无偏估计
g θ ( s , a ; b ) = △ ▽ θ ln π θ ( a ∣ s ) ⋅ [ Q π θ ( s , a ) − b ] g_\theta(s,a;b) \stackrel{\triangle}{=} \triangledown_{\theta}\ln \pi_\theta(a|s) \cdot \Big[Q_{\pi_\theta}(s,a)-b\Big] gθ(s,a;b)=△▽θlnπθ(a∣s)⋅[Qπθ(s,a)−b] 其中不依赖于 A A A 的任意函数 b b b 就是所谓的基线(baseline),它的引入不会影响策略梯度(期望不变),但会影响随机策略梯度 g θ ( s , a ; b ) g_\theta(s,a;b) gθ(s,a;b),进而影响随机策略梯度的方差
Var = E S , A [ ∥ g θ ( s , a ; b ) − ∇ θ J ( θ ) ∥ 2 ] \operatorname{Var}=\mathbb{E}_{S, A}\left[\left\|g_\theta(s,a;b) -\nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta})\right\|^{2}\right] Var=ES,A[∥gθ(s,a;b)−∇θJ(θ)∥2] 如果 b b b 很接近 Q π θ ( s , a ; b ) Q_{\pi_\theta}(s, a;b) Qπθ(s,a;b) 关于 a a a 的均值,那么方差会比较小。因此 b = V π θ ( s ) b = V_{\pi_\theta}(s) b=Vπθ(s) 是很好的基线
2.2 REINFORCE with baseline
- 我们使用 2.1 节得到的带基线的随机策略梯度 g θ ( s , a ; b ) g_\theta(s,a;b) gθ(s,a;b) 改写前文的 REINFORCR 算法,基线设置为 b = V π θ ( s ) b = V_{\pi_\theta}(s) b=Vπθ(s),即
g θ ( s , a ) = △ ▽ θ ln π θ ( a ∣ s ) ⋅ [ Q π θ ( s , a ) − V π θ ( s ) ] g_\theta(s,a) \stackrel{\triangle}{=} \triangledown_{\theta}\ln \pi_\theta(a|s) \cdot \Big[Q_{\pi_\theta}(s,a)-V_{\pi_\theta}(s)\Big] gθ(s,a)=△▽θlnπθ(a∣s)⋅[Qπθ(s,a)−Vπθ(s)] 其中 Q π θ ( s , a ) Q_{\pi_\theta}(s,a) Qπθ(s,a) 仍然和 REINFORCR 一样使用轨迹的真实 return u u u 来估计, V π θ ( s ) V_{\pi_\theta}(s) Vπθ(s) 则引入一个价值网络 v ω v_\omega vω 来估计,估计方式为 MC(而非 TD bootstrap)
2.2.1 伪代码
- 每轮迭代我们用当前策略 π θ \pi_\theta πθ 交互得到一条轨迹,然后计算出每一个 transition ( s , a , r , s ′ ) (s,a,r,s') (s,a,r,s′) 对应的 return u u u,首先用 u u u 作为标签用 mse loss 优化价值网络 v ω v_\omega vω(这样价值网络可以更好地估计 V π θ V_{\pi_\theta} Vπθ),然后利用更新后的 v w v_w vw 计算 g θ ( s , a ) g_\theta(s,a) gθ(s,a) 来更新策略网络 π θ \pi_\theta πθ。伪代码如下
初始化策略网络 π θ 和价值网络 v ω f o r e p i s o d e e = 1 → E d o : 用当前策略 π θ 交互一条轨迹 s 1 , a 1 , r 1 , . . . , s n , a n , r n 计算所有 r e t u r n u t = ∑ k = t m γ k − t r k , t = 1 , 2 , . . . , n 更新 v ω 参数 l ω = 1 2 n ∑ t = 1 n [ v ω ( s t ) − u t ] 2 更新 π θ 参数 θ ← θ + β ⋅ ▽ θ ln π θ ( a t ∣ s t ) ⋅ ( u t − v ω ( s t ) ) , t = 1 , 2 , . . . , n e n d f o r \begin{aligned} &初始化策略网络 \space \pi_\theta \space 和价值网络 \space v_\omega \\ &for \space\space episode \space\space e=1 \rightarrow E \space\space do :\\ &\quad\quad 用当前策略 \pi_{\theta} 交互一条轨迹\space s_1, a_1, r_1,...,s_n, a_n, r_n \\ & \quad\quad 计算所有 \space return \space u_t = \sum_{k=t}^m \gamma^{k-t} r_k, \space t=1,2,...,n\\ &\quad\quad 更新 \space v_\omega \space 参数 \space l_\omega = \frac{1}{2n}\sum_{t=1}^n\Big[v_\omega(s_t) - u_t \Big]^2\\ &\quad\quad更新 \space \pi_\theta \space参数\space \theta \leftarrow \theta + \beta ·\triangledown_{\theta}\ln \pi_\theta(a_t|s_t) \cdot \big(u_t - v_\omega(s_t)\big), \space t=1,2,...,n \\ &end \space\space for \end{aligned} 初始化策略网络 πθ 和价值网络 vωfor episode e=1→E do:用当前策略πθ交互一条轨迹 s1,a1,r1,...,sn,an,rn计算所有 return ut=k=t∑mγk−trk, t=1,2,...,n更新 vω 参数 lω=2n1t=1∑n[vω(st)−ut]2更新 πθ 参数 θ←θ+β⋅▽θlnπθ(at∣st)⋅(ut−vω(st)), t=1,2,...,nend for
2.2.2 用 REINFORCE with baseline 方法解决 CartPole 问题
-
定义策略网络和价值网络
class PolicyNet(torch.nn.Module):''' 策略网络是一个两层 MLP '''def __init__(self, input_dim, hidden_dim, output_dim):super(PolicyNet, self).__init__()self.fc1 = torch.nn.Linear(input_dim, hidden_dim)self.fc2 = torch.nn.Linear(hidden_dim, output_dim)def forward(self, x):x = F.relu(self.fc1(x)) # (1, hidden_dim)x = F.softmax(self.fc2(x), dim=1) # (1, output_dim)return xclass VNet(torch.nn.Module):''' 价值网络是一个两层 MLP '''def __init__(self, input_dim, hidden_dim):super(VNet, self).__init__()self.fc1 = torch.nn.Linear(input_dim, hidden_dim)self.fc2 = torch.nn.Linear(hidden_dim, 1)def forward(self, x):x = F.relu(self.fc1(x))x = self.fc2(x)return -
定义 REINFORCE with baseline agent
class REINFORCE_Baseline(torch.nn.Module):def __init__(self, state_dim, hidden_dim, action_range, lr_policy, lr_value, gamma, device):super().__init__()self.policy_net = PolicyNet(state_dim, hidden_dim, action_range).to(device)self.v_net = VNet(state_dim, hidden_dim).to(device)self.optimizer_policy = torch.optim.Adam(self.policy_net.parameters(), lr=lr_policy) # 使用Adam优化器self.optimizer_value = torch.optim.Adam(self.v_net.parameters(), lr=lr_value) # 使用Adam优化器self.gamma = gammaself.device = devicedef take_action(self, state): # 根据动作概率分布随机采样state = torch.tensor(state, dtype=torch.float).to(self.device)state = state.unsqueeze(0)probs = self.policy_net(state).squeeze()action_dist = torch.distributions.Categorical(probs)action = action_dist.sample()return action.item()def update(self, transition_dict):G, returns = 0, []for reward in reversed(transition_dict['rewards']):G = self.gamma * G + rewardreturns.insert(0, G)rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device).squeeze() # (bsz, )returns = torch.tensor(returns, dtype=torch.float).view(-1, 1).to(self.device).squeeze() # (bsz, )states = torch.tensor(np.array(transition_dict['states']), dtype=torch.float).to(self.device) # (bsz, state_dim)actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device) # (bsz, action_dim)# 梯度清零self.optimizer_value.zero_grad()self.optimizer_policy.zero_grad()# 更新价值网络value_predicts = self.v_net(states).squeeze() # (bsz, )value_loss = torch.mean(F.mse_loss(value_predicts, returns)) value_loss.backward()self.optimizer_value.step()# 更新策略网络, 从轨迹最后一步起往前计算 return,每步回传累计梯度 for i in reversed(range(len(rewards))):action = actions[i]state = states[i]value = self.v_net(state).squeeze() # 使用更新过的价值网络预测价值G = returns[i] # (state_dim, )probs = self.policy_net(state.unsqueeze(0)).squeeze() # (action_range, )log_prob = torch.log(probs[action])policy_loss = -log_prob * (G - value.detach()) # value 是 v_net 给出的,将其 detach 以确保只更新 policy 参数policy_loss.backward() self.optimizer_policy.step() -
进行训练并绘制性能曲线
if __name__ == "__main__":def moving_average(a, window_size):''' 生成序列 a 的滑动平均序列 '''cumulative_sum = np.cumsum(np.insert(a, 0, 0)) middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_sizer = np.arange(1, window_size-1, 2)begin = np.cumsum(a[:window_size-1])[::2] / rend = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]return np.concatenate((begin, middle, end))def set_seed(env, seed=42):''' 设置随机种子 '''env.action_space.seed(seed)env.reset(seed=seed)random.seed(seed)np.random.seed(seed)torch.manual_seed(seed)state_dim = 4 # 环境观测维度action_range = 2 # 环境动作空间大小lr_policy = 2e-3lr_value = 3e-3num_episodes = 500hidden_dim = 64gamma = 0.98device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")# build environmentenv_name = 'CartPole-v0'env = gym.make(env_name, render_mode='rgb_array')check_env(env.unwrapped) # 检查环境是否符合 gym 规范set_seed(env, 42)# build agentagent = REINFORCE_Baseline(state_dim, hidden_dim, action_range, lr_policy, lr_value, gamma, device)# start trainingreturn_list = []for i in range(10):with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:for i_episode in range(int(num_episodes / 10)):episode_return = 0transition_dict = {'states': [],'actions': [],'next_states': [],'rewards': [],'dones': []}state, _ = env.reset()# 以当前策略交互得到一条轨迹while True:action = agent.take_action(state)next_state, reward, terminated, truncated, _ = env.step(action)transition_dict['states'].append(state)transition_dict['actions'].append(action)transition_dict['next_states'].append(next_state)transition_dict['rewards'].append(reward)transition_dict['dones'].append(terminated or truncated)state = next_stateepisode_return += rewardif terminated or truncated:env.render()break#env.render()# 用当前策略收集的数据进行 on-policy 更新agent.update(transition_dict)# 更新进度条return_list.append(episode_return)pbar.set_postfix({'episode':'%d' % (num_episodes / 10 * i + i_episode + 1),'return':'%.3f' % episode_return,'ave return':'%.3f' % np.mean(return_list[-10:])})pbar.update(1)# show policy performencemv_return_list = moving_average(return_list, 29)episodes_list = list(range(len(return_list)))plt.figure(figsize=(12,8))plt.plot(episodes_list, return_list, label='raw', alpha=0.5)plt.plot(episodes_list, mv_return_list, label='moving ave')plt.xlabel('Episodes')plt.ylabel('Returns')plt.title(f'{agent._get_name()} on CartPole-V0')plt.legend()plt.savefig(f'./result/{agent._get_name()}.png')plt.show()
2.2.3 性能
- 对比前文介绍的普通 REINFORCE 方法和以上 REINFORCE with baseline 方法的性能曲线,如下

可见引入 baseline 有效降低了方差,且加快了收敛速度
2.3 Advantage Actor-Critic (A2C)
- 我们使用 2.1 节得到的带基线的随机策略梯度 g θ ( s , a ; b ) g_\theta(s,a;b) gθ(s,a;b) 改写前文的 REINFORCR 算法,基线设置为 b = V π θ ( s ) b = V_{\pi_\theta}(s) b=Vπθ(s),即
g θ ( s , a ) = △ ▽ θ ln π θ ( a ∣ s ) ⋅ [ Q π θ ( s , a ) − V π θ ( s ) ] g_\theta(s,a) \stackrel{\triangle}{=} \triangledown_{\theta}\ln \pi_\theta(a|s) \cdot \Big[Q_{\pi_\theta}(s,a)-V_{\pi_\theta}(s)\Big] gθ(s,a)=△▽θlnπθ(a∣s)⋅[Qπθ(s,a)−Vπθ(s)] 其中 Q π θ ( s , a ) − V π θ ( s ) Q_{\pi_\theta}(s,a)-V_{\pi_\theta}(s) Qπθ(s,a)−Vπθ(s) 被称作优势函数 (advantage function),因此基于上面公式得到的 actor-critic 方法被称为 advantage actor-critic (A2C)。A2C 属于 actor-critic 方法,有一个策略网络 π θ \pi_\theta πθ 作为 Actor 用于控制 agent 运动,还有一个价值网络 v ω v_\omega vω 作为 Critic,他的评分可以帮助 Actor 改进。两个神经网络的结构与上一节中的完全相同,但是本节和上一节用不同的方法训练两个神经网络
2.3.1 伪代码
- 这里训练价值网络时不像 REINFORCE with baseline 那样直接优化 mse loss 去靠近真实 return(MC),而是用 mse loss 去优化 Sarsa TD error。具体而言,给定 transition ( s , a , r , s ′ ) (s,a,r,s') (s,a,r,s′),如下得到 TD error 的 mse loss
l ω = 1 2 [ v ω ( s ) − ( r + v ω ( s ′ ) ) ] 2 l_\omega = \frac{1}{2}\Big[v_\omega(s) - \big(r+v_\omega(s')\big)\Big]^2 lω=21[vω(s)−(r+vω(s′))]2 - 训练策略网络时利用 Bellman 公式得到 Q Q Q 和 V V V 的关系
Q π ( s t , a t ) = E S t + 1 ∼ p ( ⋅ ∣ s t , a t ) [ R t + γ V π ( S t + 1 ) ] Q_{\pi}\left(s_{t}, a_{t}\right) = \mathbb{E}_{S_{t+1}\sim p(·|s_t,a_t)}\Big[R_t + \gamma V_\pi(S_{t+1})\Big] Qπ(st,at)=ESt+1∼p(⋅∣st,at)[Rt+γVπ(St+1)] 把带基线的随机策略梯度中的 Q π θ ( s , a ) Q_{\pi_\theta}(s,a) Qπθ(s,a) 进行替换
g θ ( s , a ) = ▽ θ ln π θ ( a ∣ s ) ⋅ [ Q π θ ( s , a ) − V π θ ( s ) ] = ▽ θ ln π θ ( a ∣ s ) ⋅ [ E S t + 1 [ R t + γ V π θ ( S t + 1 ) ] − V π θ ( s ) ] \begin{aligned} \boldsymbol{g}_\theta\left(s,a\right) & =\triangledown_{\theta}\ln \pi_\theta(a|s) \cdot \Big[Q_{\pi_\theta}(s,a)-V_{\pi_\theta}(s)\Big] \\ & = \triangledown_{\theta}\ln \pi_\theta(a|s) \cdot \Big[\mathbb{E}_{S_{t+1}}\left[R_t+\gamma V_{\pi_\theta}\left(S_{t+1}\right)\right]-V_{\pi_\theta}(s)\Big] \end{aligned} gθ(s,a)=▽θlnπθ(a∣s)⋅[Qπθ(s,a)−Vπθ(s)]=▽θlnπθ(a∣s)⋅[ESt+1[Rt+γVπθ(St+1)]−Vπθ(s)] 使用真实的 transition ( s , a , r , s ′ ) (s,a,r,s') (s,a,r,s′) 进行 MC 近似,得到随机策略梯度
g ~ θ ( s , a ) ≜ [ r + γ ⋅ v ω ( s ′ ) − v ω ( s ) ⏟ T D Error ] ⋅ ∇ θ ln π θ ( a ∣ s ) . \tilde{\boldsymbol{g}}_\theta\left(s,a\right) \triangleq[\underbrace{r+\gamma \cdot v_\omega\left(s'\right)-v_\omega\left(s\right)}_{\mathrm{TD} \text { Error} }] \cdot \nabla_{\boldsymbol{\theta}} \ln \pi_\theta\left(a \mid s\right) . g~θ(s,a)≜[TD Error r+γ⋅vω(s′)−vω(s)]⋅∇θlnπθ(a∣s). 用这个随机策略梯度做梯度上升即可优化策略网络 - A2C 的伪代码如下
初始化策略网络 π θ 和价值网络 v ω f o r e p i s o d e e = 1 → E d o : 用当前策略 π θ 交互一条轨迹 s 1 , a 1 , r 1 , . . . , s n , a n , r n 计算所有 TD erro r δ t = r t + γ ⋅ v ω ( s t + 1 ) − v ω ( s t ) 更新 v ω 参数 l ω = 1 2 n ∑ t = 1 n [ δ t ] 2 更新 π θ 参数 θ ← θ + β ⋅ ▽ θ ln π θ ( a t ∣ s t ) ⋅ δ t , t = 1 , 2 , . . . , n e n d f o r \begin{aligned} &初始化策略网络 \space \pi_\theta \space 和价值网络 \space v_\omega \\ &for \space\space episode \space\space e=1 \rightarrow E \space\space do :\\ &\quad\quad 用当前策略 \pi_{\theta} 交互一条轨迹\space s_1, a_1, r_1,...,s_n, a_n, r_n \\ & \quad\quad 计算所有 \space \text{TD erro}r \space \delta_t = r_t+\gamma \cdot v_\omega\left(s_{t+1}\right)-v_\omega\left(s_t\right)\\ &\quad\quad 更新 \space v_\omega \space 参数 \space l_\omega = \frac{1}{2n}\sum_{t=1}^n\Big[ \delta_t \Big]^2\\ &\quad\quad更新 \space \pi_\theta \space参数\space \theta \leftarrow \theta + \beta ·\triangledown_{\theta}\ln \pi_\theta(a_t|s_t) · \delta_t , \space t=1,2,...,n \\ &end \space\space for \end{aligned} 初始化策略网络 πθ 和价值网络 vωfor episode e=1→E do:用当前策略πθ交互一条轨迹 s1,a1,r1,...,sn,an,rn计算所有 TD error δt=rt+γ⋅vω(st+1)−vω(st)更新 vω 参数 lω=2n1t=1∑n[δt]2更新 πθ 参数 θ←θ+β⋅▽θlnπθ(at∣st)⋅δt, t=1,2,...,nend for
2.3.2 用 A2C 方法解决 CartPole 问题
- 只需要重新定义 A2C agent,其他代码全部和 REINFORCE with baseline 一致
class A2C(torch.nn.Module):def __init__(self, state_dim, hidden_dim, action_range, actor_lr, critic_lr, gamma, device):super().__init__()self.gamma = gammaself.device = deviceself.actor = PolicyNet(state_dim, hidden_dim, action_range).to(device)self.critic = VNet(state_dim, hidden_dim).to(device) self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)def take_action(self, state):state = torch.tensor(state, dtype=torch.float).to(self.device)state = state.unsqueeze(0)probs = self.actor(state)action_dist = torch.distributions.Categorical(probs)action = action_dist.sample()return action.item()def update(self, transition_dict):states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)# Cirtic loss td_target = rewards + self.gamma * self.critic(next_states) * (1-dones)critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))# Actor loss td_error = td_target - self.critic(states) probs = self.actor(states).gather(1, actions)log_probs = torch.log(probs)actor_loss = torch.mean(-log_probs * td_error.detach())# 更新网络参数self.actor_optimizer.zero_grad()self.critic_optimizer.zero_grad()actor_loss.backward() critic_loss.backward() self.actor_optimizer.step() self.critic_optimizer.step()
2.3.3 性能
- 对比前文介绍的普通 Actor-Critic 方法和以上 A2C 方法的性能曲线,如下

可见普通 Actor-Critic 方法即使交互轨迹数量翻倍也难以收敛,而 A2C 收敛迅速,性能稳定
2.3.4 引入目标网络
-
之前我们讲 DQN 时提到过关于 bootstrap 迭代的一个问题
TD bootstrap 是在使用由 DQN 生成的优化目标 TD target 来优化 DQN 网络。这就导致优化目标随着训练进行不断变化,违背了监督学习的 i.i.d 原则,导致训练不稳定
A2C 中的 critic 网络同样具有此问题,为了稳定训练,我们可以像 DQN 那样引入一个参数更新频率更低的目标网络来稳定 TD target,从而稳定训练过程。考虑到 A2C 本身是 on-policy 方法,这里不适合像 DQN 那样按照一定周期去替换目标网络参数,而是应该使用加权平均的方式来更新。设引入目标网络 v w ′ v_{w'} vw′ 和更新权重 τ \tau τ,A2C 算法的伪代码变为
初始化策略网络 π θ , 价值网络 v ω 和目标网络 v ω ′ f o r e p i s o d e e = 1 → E d o : 用当前策略 π θ 交互一条轨迹 s 1 , a 1 , r 1 , . . . , s n , a n , r n 计算所有 TD erro r δ t = r t + γ ⋅ v ω ′ ( s t + 1 ) − v ω ( s t ) 更新 v ω 参数 l ω = 1 2 n ∑ t = 1 n [ δ t ] 2 更新 v ω ′ 参数 ω ′ ← τ w ′ + ( 1 − τ ) w 更新 π θ 参数 θ ← θ + β ⋅ ▽ θ ln π θ ( a t ∣ s t ) ⋅ δ t , t = 1 , 2 , . . . , n e n d f o r \begin{aligned} &初始化策略网络 \space \pi_\theta \space ,价值网络 \space v_\omega 和目标网络 \space v_{\omega'} \\ &for \space\space episode \space\space e=1 \rightarrow E \space\space do :\\ &\quad\quad 用当前策略 \pi_{\theta} 交互一条轨迹\space s_1, a_1, r_1,...,s_n, a_n, r_n \\ & \quad\quad 计算所有 \space \text{TD erro}r \space \delta_t = r_t+\gamma \cdot v_{\omega'}\left(s_{t+1}\right)-v_\omega\left(s_t\right)\\ &\quad\quad 更新 \space v_\omega \space 参数 \space l_\omega = \frac{1}{2n}\sum_{t=1}^n\Big[ \delta_t \Big]^2\\ &\quad\quad 更新 \space v_{\omega'} \space 参数 \space \omega' \leftarrow \tau w' \space + \space (1-\tau)w \\ &\quad\quad更新 \space \pi_\theta \space参数\space \theta \leftarrow \theta + \beta ·\triangledown_{\theta}\ln \pi_\theta(a_t|s_t) · \delta_t , \space t=1,2,...,n \\ &end \space\space for \end{aligned} 初始化策略网络 πθ ,价值网络 vω和目标网络 vω′for episode e=1→E do:用当前策略πθ交互一条轨迹 s1,a1,r1,...,sn,an,rn计算所有 TD error δt=rt+γ⋅vω′(st+1)−vω(st)更新 vω 参数 lω=2n1t=1∑n[δt]2更新 vω′ 参数 ω′←τw′ + (1−τ)w更新 πθ 参数 θ←θ+β⋅▽θlnπθ(at∣st)⋅δt, t=1,2,...,nend for -
带目标网络的的 A2C agent 实现如下,其他代码基本和 A2C 一致
class A2C_Target(torch.nn.Module):def __init__(self, state_dim, hidden_dim, action_range, target_weight, actor_lr, critic_lr, gamma, device):super().__init__()self.gamma = gammaself.device = deviceself.target_weight = target_weight self.actor = PolicyNet(state_dim, hidden_dim, action_range).to(device)self.critic = VNet(state_dim, hidden_dim).to(device) self.target = VNet(state_dim, hidden_dim).to(device) self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)def take_action(self, state):state = torch.tensor(state, dtype=torch.float).to(self.device)state = state.unsqueeze(0)probs = self.actor(state)action_dist = torch.distributions.Categorical(probs)action = action_dist.sample()return action.item()def update(self, transition_dict):states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)# Cirtic loss td_target = rewards + self.gamma * self.target(next_states) * (1-dones)critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))# Actor loss td_error = td_target - self.critic(states) probs = self.actor(states).gather(1, actions)log_probs = torch.log(probs)actor_loss = torch.mean(-log_probs * td_error.detach())# 更新网络参数self.actor_optimizer.zero_grad()self.critic_optimizer.zero_grad()actor_loss.backward() critic_loss.backward() self.actor_optimizer.step() self.critic_optimizer.step() # 更新 target 网络参数为 target 和 critic 的加权平均w = self.target_weight params_target = list(self.target.parameters())params_critic = list(self.critic.parameters())for i in range(len(params_target)):new_param = w * params_target[i] + (1 - w) * params_critic[i]params_target[i].data.copy_(new_param) -
当 τ = 0.95 \tau=0.95 τ=0.95 时性能较好,和 A2C 相比如下

可见引入目标网络后收敛更快,收敛后也更稳定
3. 总结
- 在策略梯度中加入基线 (baseline) 可以降低方差,显著提升实验效果。实践中常用 b = V π ( s ) b = V_\pi(s) b=Vπ(s) 作为 baseline。
- 可以用基线来改进 REINFORCE 算法。这时我们仍然用真实 return 来估计策略梯度中的 Q Q Q 价值,并引入价值网络 v w v_w vw,使用 MC 方法来估计状态价值函数 V π ( s ) V_\pi(s) Vπ(s) 作为 baseline。如此计算出随机策略梯度后,和原始 REINFORCE 一样用随机策略梯度上升更新策略网络 π θ ( a ∣ s ) π_\theta(a|s) πθ(a∣s)
- 可以用基线来改进 actor-critic,得到的方法叫做 advantage actor-critic (A2C)。A2C 也有一个策略网络 π θ ( a ∣ s ) π_\theta(a|s) πθ(a∣s) 和一个价值网络 v ω ( s ) v_\omega(s) vω(s)。它使用 TD 算法(Sarsa)来更新价值网络计算随机策略梯度,并同样用梯度上升更新策略网络 π θ ( a ∣ s ) π_\theta(a|s) πθ(a∣s)。为了稳定 TD bootstarp,可以像 DQN 那样引入目标价值网络 v ω ′ ( s ) v_{\omega'}(s) vω′(s) 用于计算 TD target,目标网络通过加权平均方式进行 soft update,可以进一步提高 A2C 的性能
相关文章:

RL 实践(6)—— CartPole【REINFORCE with baseline A2C】
本文介绍 REINFORCE with baseline 和 A2C 这两个带 baseline 的策略梯度方法,并在 CartPole-V0 上验证它们和无 baseline 的原始方法 REINFORCE & Actor-Critic 的优势参考:《动手学强化学习》完整代码下载:7_[Gym] CartPole-V0 (REINFO…...
Python numpy库的应用、matplotlib绘图、opencv的应用
numpy import numpy as npl1 [1, 2, 3, 4, 5]# array():将列表同构成一个numpy的数组 l2 np.array(l1) print(type(l2)) print(l2) # ndim : 返回数组的轴数(维度数) # shape:返回数组的形状,用元组表示;元组的元素…...

SpringBoot 如何进行 统一异常处理
在Spring Boot中,可以通过自定义异常处理器来实现统一异常处理。异常处理器能够捕获应用程序中抛出的各种异常,并提供相应的错误处理和响应。 Spring Boot提供了ControllerAdvice注解,它可以将一个类标记为全局异常处理器。全局异常处理器能…...

数据库索引优化与查询优化——醍醐灌顶
索引优化与查询优化 哪些维度可以进行数据库调优 索引失效、没有充分利用到索引-一索引建立关联查询太多JOIN (设计缺陷或不得已的需求) --SQL优化服务器调优及各个参数设置 (缓冲、线程数等)–调整my.cnf数据过多–分库分表 关于数据库调优的知识点非常分散。不同的 DBMS&a…...
与知识蒸馏)
Student and Teacher network(学生—教师网络)与知识蒸馏
Student and Teacher network指一个较小且较简单的模型(学生)被训练来模仿一个较大且较复杂的模型(教师)的行为或预测。教师网络通常是一个经过训练在大型数据集上并在特定任务上表现良好的模型。而学生网络被设计成计算效率高且参…...

FPGA——PLD的区别以及各自的特点
目录 一、概述二、PLD的优点三、PLD的分类1、PROM(可编程只读存储器):2、PAL(可编程阵列逻辑)3、GAL(通用阵列逻辑)4、CPLD (复杂PLD)5、FPGA(现场可编程门阵…...
八、Kafka时间轮与常见问题
Kafka与时间轮 Kafka中存在大量的延时操作。 1、发送消息-超时重试机制 2、ACKS 用于指定分区中必须要有多少副本收到这条消息,生产者才认为写入成功(延时 等) Kafka并没有使用JDK自带的Timer或者DelayQueue来实现延迟的功能,而…...
Web端即时通讯技术(SEE,webSocket)
目录 背景简介个人见解被动推送轮询简介实现 长轮询(comet)简介实现 比较 主动推送长连接(SSE)简介实现GETPOST 效果 webSocket简介WebSocket的工作原理:WebSocket的主要优点:WebSocket的主要缺点: 实现用法一用法二 **效果** 比较…...
脑电信号处理与特征提取——4.脑电信号的预处理及数据分析要点(彭微微)
目录 四、脑电信号的预处理及数据分析要点 4.1 脑电基础知识回顾 4.2 伪迹 4.3 EEG预处理 4.3.1 滤波 4.3.2 重参考 4.3.3 分段和基线校正 4.3.4 坏段剔除 4.3.5 坏导剔除/插值 4.3.6 独立成分分析ICA 4.4 事件相关电位(ERPs) 4.4.1 如何获…...
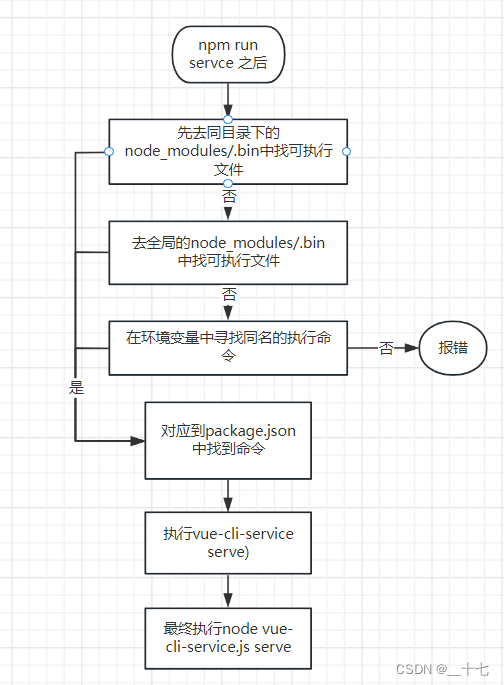
分析npm run serve之后发生了什么?
首先需要明白的是,当你在终端去运行 npm run ****,会是什么过程。 根据上图的一个流程,就可以衍生出很多问题。 1,为什么不直接运行vue-cli-service serve? 因为直接运行 vue-cli-service serve,会报错,…...

LINUX上操作redis 用shell7
LINUX上操作redis 用shell7 步骤1:连接到Linux服务器步骤2:安装和配置Redis步骤3:连接到Redis服务器步骤4:操作Redis数据步骤5:断开与Redis服务器的连接 步骤1:连接到Linux服务器 首先,需要使用…...

Python的threading模块
为引入多线程的概念,下面是一个例子: import time, datetimestartTime datetime.datetime(2024, 1, 1, 0, 0, 0) while datetime.datetime.now() < startTime:time.sleep(1)print(Program now starting on NewYear2024) 在等待time.sleep()的循环调…...

HTML5 的离线储存怎么使用,工作原理
TML5提供了一种称为离线储存(Offline Storage)的功能,它允许网页在离线时缓存和存储数据,以便用户可以在没有网络连接的情况下访问这些数据。离线储存是通过使用Web Storage API或者应用程序缓存(Application Cache&am…...

FTP文件传输协议与DHCP
基本概念 主机之间传输文件是IP网络的一个重要功能 互联网早期,最通用方式就是使用FTP(File Transfer Protocol,文件传输协议)以及(Trivial File Transfer Protocol,简单文件传输协议) FTP采用…...

【UE5 多人联机教程】06-显示玩家名称
效果 可以看到玩家输入各自的名称,会显示到自己控制的角色头上。但是目前有一个BUG就是,当客户端加入游戏时会多创建一个服务端的角色。 步骤 1. 打开“BP_ThirdPersonCharacter”,添加一个控件组件,用于显示玩家名称 作为网格体…...

Rust vs Go:常用语法对比(五)
题图来自 Rust vs Go 2023[1] 81. Round floating point number to integer Declare integer y and initialize it with the rounded value of floating point number x . Ties (when the fractional part of x is exactly .5) must be rounded up (to positive infinity). 按规…...

Flutter 扩展函数项目实用之封装SizedBox
Flutter里扩展函数可以用简化代码写法,关键字为extension,伪代码写法如下: extension 扩展类名 on 扩展类型 { //扩展方法 } 在Flutter页面里实现控件间距会常用到SizedBox,可使用扩展函数封装来达到简化代码的目的࿰…...

EMC学习笔记(二十)EMC常用元件简单介绍(二)
EMC常用元件简单介绍(二) 1.瞬态抑制二极管(TVS)2.气体放电管3.半导体放电管 电磁兼容性元件是解决电磁干扰发射和电磁敏感度问题的关键,正确选择和使用这些元件是做好电磁兼容性设计的前提。由于每一种电子元件都有它各自的特性,…...
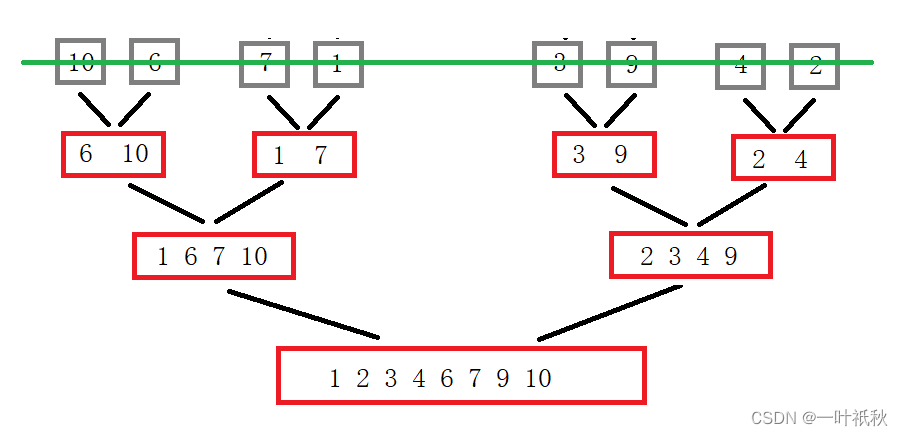
基本排序算法
目录 一,插入排序 二,希尔排序 三,选择排序 四,冒泡排序 五,快排 5.1 Hoare法 5.2 挖坑法 5.3 指针法 5.4 非递归写法 六,归并排序 6.1 递归 6.2 非递归 一,插入排序 基本思想&…...
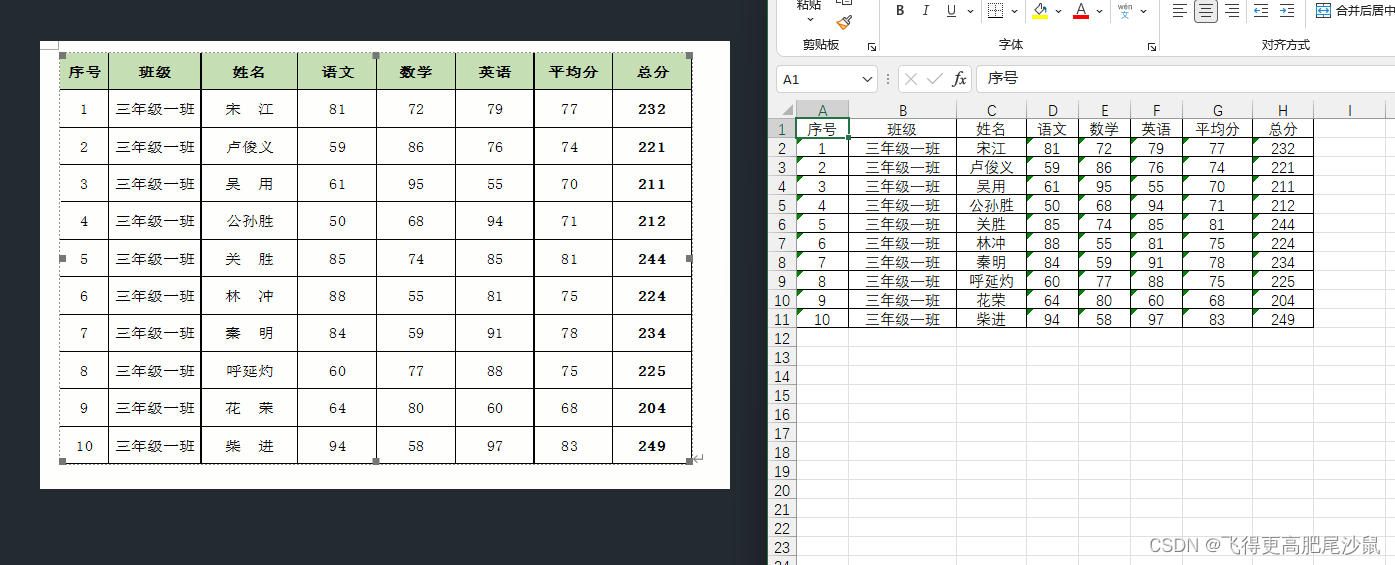
python调用百度ai将图片/pdf识别为表格excel
python调用百度ai将图片识别为表格excel 表格文字识别(异步接口)图片转excel 表格文字识别V2图片/pdf转excel通用 表格文字识别(异步接口) 图片转excel 百度ai官方文档:https://ai.baidu.com/ai-doc/OCR/Ik3h7y238 使用的是表格文字识别(异步接口),同步…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
