LeetCode 2050. Parallel Courses III【记忆化搜索,动态规划,拓扑排序】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个整数 n ,表示有 n 节课,课程编号从 1 到 n 。同时给你一个二维整数数组 relations ,其中 relations[j] = [prevCoursej, nextCoursej] ,表示课程 prevCoursej 必须在课程 nextCoursej 之前 完成(先修课的关系)。同时给你一个下标从 0 开始的整数数组 time ,其中 time[i] 表示完成第 (i+1) 门课程需要花费的 月份 数。
请你根据以下规则算出完成所有课程所需要的 最少 月份数:
- 如果一门课的所有先修课都已经完成,你可以在 任意 时间开始这门课程。
- 你可以 同时 上 任意门课程 。
请你返回完成所有课程所需要的 最少 月份数。
注意: 测试数据保证一定可以完成所有课程(也就是先修课的关系构成一个有向无环图)。
示例 1:

输入:n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出:8
解释:上图展示了输入数据所表示的先修关系图,以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月,课程 2 花费 2 个月。
所以,最早开始课程 3 的时间是月份 3 ,完成所有课程所需时间为 3 + 5 = 8 个月。
示例 2:
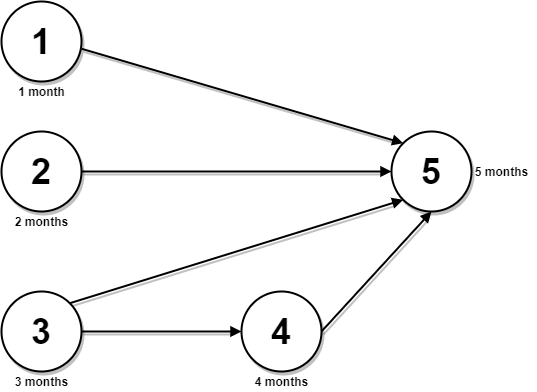
输入:n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出:12
解释:上图展示了输入数据所表示的先修关系图,以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ,2 和 3 。
在月份 1,2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始,也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1,2,3 和 4 之后开始,也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。
提示:
1 <= n <= 5 * 10^40 <= relations.length <= min(n * (n - 1) / 2, 5 * 10^4)relations[j].length == 21 <= prevCoursej, nextCoursej <= nprevCoursej != nextCoursej- 所有的先修课程对
[prevCoursej, nextCoursej]都是 互不相同 的。 time.length == n1 <= time[i] <= 10^4- 先修课程图是一个有向无环图。
本题的实质是求 AOE 图上的最长路径。相似题目:
- 1857. 有向图中最大颜色值
解法1 记忆化搜索
要求出完成所有课程的最少月份数,可以求出每门课程的最少月份数,然后求出最大值。首先根据 r e l a t i o n s relations relations,构建先修课邻接表表 p r e v prev prev, p r e v [ i ] prev[i] prev[i] 就表示课程 i i i 的所有的先修课。定义函数 d p dp dp ,输入参数为 i i i ,返回完成课程 i i i 所需的最少月份数。
- 如果一门课程 i i i 没有先修课要求,那么完成它的最少月份数就是 t i m e [ i − 1 ] time[i - 1] time[i−1] 。
- 如果一门课有先修课时,完成它的最少月份数就是在它的所有先修课的最少完成月份的最大值的基础上,再加上 t i m e [ i − 1 ] time[i - 1] time[i−1],即 dp [ i ] = max ( d p [ j ] ) + time [ i − 1 ] , j ∈ prev [ i ] \textit{dp}[i] = \textit{max}(dp[j])+\textit{time}[i-1], j\in \textit{prev}[i] dp[i]=max(dp[j])+time[i−1],j∈prev[i] 。
可以运用记忆化搜索的技巧,求出每门课的最少完成月份数。因为运用了记忆化搜索,每门课的最少完成月份数最多只会被计算一次。
class Solution {
public:int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {int mx = 0;vector<vector<int>> prev(n + 1);for (auto &r : relations) {int x = r[0], y = r[1];prev[y].emplace_back(x);}unordered_map<int, int> rec;function<int(int)> dp = [&](int i) -> int {if (!rec.count(i)) {int cur = 0;for (int p : prev[i]) cur = max(cur, dp(p));cur += time[i - 1];rec[i] = cur;}return rec[i];};for (int i = 1; i <= n; ++i) mx = max(mx, dp(i));return mx;}
};
复杂度分析:
- 时间复杂度: O ( m + n ) O(m +n) O(m+n),其中 O ( m ) O(m) O(m) 是数组 r e l a t i o n s relations relations 长度。需要构建先修课邻接表表,并且计算每个课程的最少月份数。因为每个课程只会被计算一次,因此相当于是每个 r e l a t i o n relation relation 会被遍历一次。
- 空间复杂度: O ( m + n ) O(m +n) O(m+n),先修课邻接表表的空间复杂度是 O ( m + n ) O(m +n) O(m+n),记忆化搜索的空间复杂度是 O ( n ) O(n) O(n) 。
解法2 动态规划
定义 d p [ i ] dp[i] dp[i] 表示完成第 i i i 门课程需要花费的最少月份数。根据题意,只有当 i i i 的所有先修课程都完成时,才可以开始学习第 i i i 门课程,并且可以立即开始。
因此,其中 j j j 是 i i i 的先修课程 f [ i ] = time [ i ] + max j f [ j ] f[i]=\textit{time}[i] + \max_{j} f[j] f[i]=time[i]+jmaxf[j]
由于题目保证图是一个有向无环图,所以一定存在拓扑序。我们可以在计算拓扑序的同时,计算状态转移。
具体来说,设当前节点为 u u u ,我们可以在计算出 d p [ u ] dp[u] dp[u] 后,更新 v v v 的所有先修课程耗时的最大值,这里 u u u 是 v v v 的先修课程。答案就是所有 d p [ i ] dp[i] dp[i] 的最大值。
class Solution {
private:vector<vector<int>> g;
public:int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {g.resize(n);vector<int> ind(n);for (vector<int>& r : relations) {int x = r[0] - 1, y = r[1] - 1;g[x].push_back(y); // 建图++ind[y];}// 拓扑排序 queue<int> q;for (int i = 0; i < n; ++i)if (ind[i] == 0) // 没有先修课q.push(i); vector<int> dp(n);int ans = 0;while (!q.empty()) {int u = q.front(); q.pop(); // u出队意味着u的所有先修课都上完了// 出队的顺序就是拓扑序dp[u] += time[u]; // 加上当前课程的时间就得到了最终的dp[u]ans = max(ans, dp[u]);for (int v : g[u]) {dp[v] = max(dp[u], dp[v]); // 更新dp[v]的所有先修课程耗时的最大值if (--ind[v] == 0) { // v的先修课已上完q.push(v); }}}return ans;}
};
复杂度分析:
- 时间复杂度: O ( m + n ) O(m+n) O(m+n) ,其中 O ( m ) O(m) O(m) 为 r e l a t i o n s relations relations 的长度。
- 空间复杂度: O ( m + m ) O(m+m) O(m+m) 。
相关文章:

LeetCode 2050. Parallel Courses III【记忆化搜索,动态规划,拓扑排序】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
ETHERNET/IP转RS485/RS232网关什么是EtherNet/IP?
网络数据传输遇到的协议不同、数据互通麻烦等问题,一直困扰着大家。然而,现在有一种神器——捷米JM-EIP-RS485/232,它将ETHERNET/IP网络和RS485/RS232总线连接在一起,让数据传输更加便捷高效。 那么,它是如何实现这一功…...

使用node内置test runner,和 Jest say 拜拜
参考 https://nodejs.org/dist/latest-v20.x/docs/api/test.html#test-runner 在之前,我们写单元测试,必须安装第三方依赖包,而从node 20.0.0 版本之后,可以告别繁琐的第三方依赖包啦,可直接使用node的内置test runner…...

《面试1v1》Kafka的架构设计是什么样子
🍅 作者简介:王哥,CSDN2022博客总榜Top100🏆、博客专家💪 🍅 技术交流:定期更新Java硬核干货,不定期送书活动 🍅 王哥多年工作总结:Java学习路线总结…...

比较常见CPU的区别:Intel、ARM、AMD
一、开发公司不同 1、Intel:是英特尔公司开发的中央处理器,有移动、台式、服务器三个系列。 2、ARM:是英国Acorn有限公司设计的低功耗成本的第一款RISC微处理器。 3、AMD:由AMD公司生产的处理器。 二、技术不同 1、Intel&…...
CAN转EtherNet/IP网关can协议是什么意思
你是否曾经遇到过不同的总线协议难以互相通信的问题?远创智控的YC-EIP-CAN网关为你解决了这个烦恼! 远创智控YC-EIP-CAN通讯网关是一款自主研发的设备,它能够将各种CAN总线和ETHERNET/IP网络连接起来,解决不同总线协议之间的通信…...
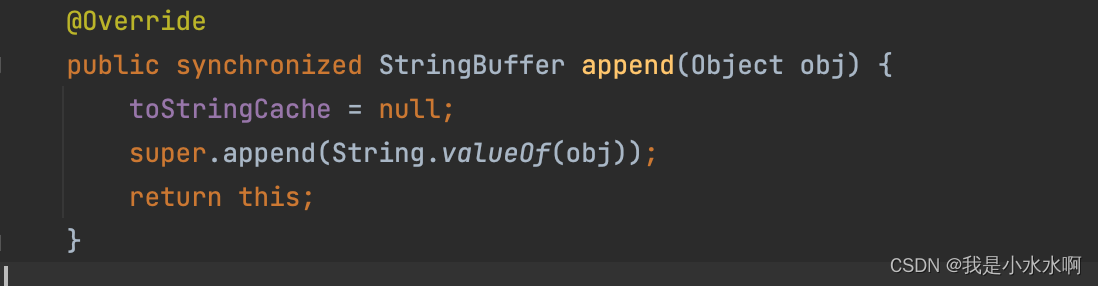
java可变字符序列:StringBuffer、StringBuilder
文章目录 StringBuffer与StringBuilder的理解StringBuilder、StringBuffer的API StringBuffer与StringBuilder的理解 因为String对象是不可变对象,虽然可以共享常量对象,但是对于频繁字符串的修改和拼接操作,效率极低,空间消耗也…...
Mac/win开发快捷键、vs插件、库源码、开发中的专业名词
目录 触控板手势(2/3指) 鼠标右键 快捷键 鼠标选择后shift⬅️→改变选择 mac command⬅️:删除←边的全部内容 commadtab显示下栏 commandshiftz向后撤回 commandc/v复制粘贴 command ⬅️→回到行首/末 commandshift3/4截图 飞…...

linux 系统编程
C标准函数与系统函数的区别 什么是系统调用 由操作系统实现并提供给外部应用程序的编程接口。(Application Programming Interface,API)。是应用程序同系统之间数据交互的桥梁。 一个helloworld如何打印到屏幕。 每一个FILE文件流(标准C库函数ÿ…...

Python策略模式介绍、使用方法
一、Python策略模式介绍 Python策略模式(Strategy Pattern)是一种软件设计模式,用于通过将算法封装为独立的对象,而使得它们可以在运行时动态地相互替换。该模式使得算法的变化独立于使用它们的客户端,从而达到代码的…...
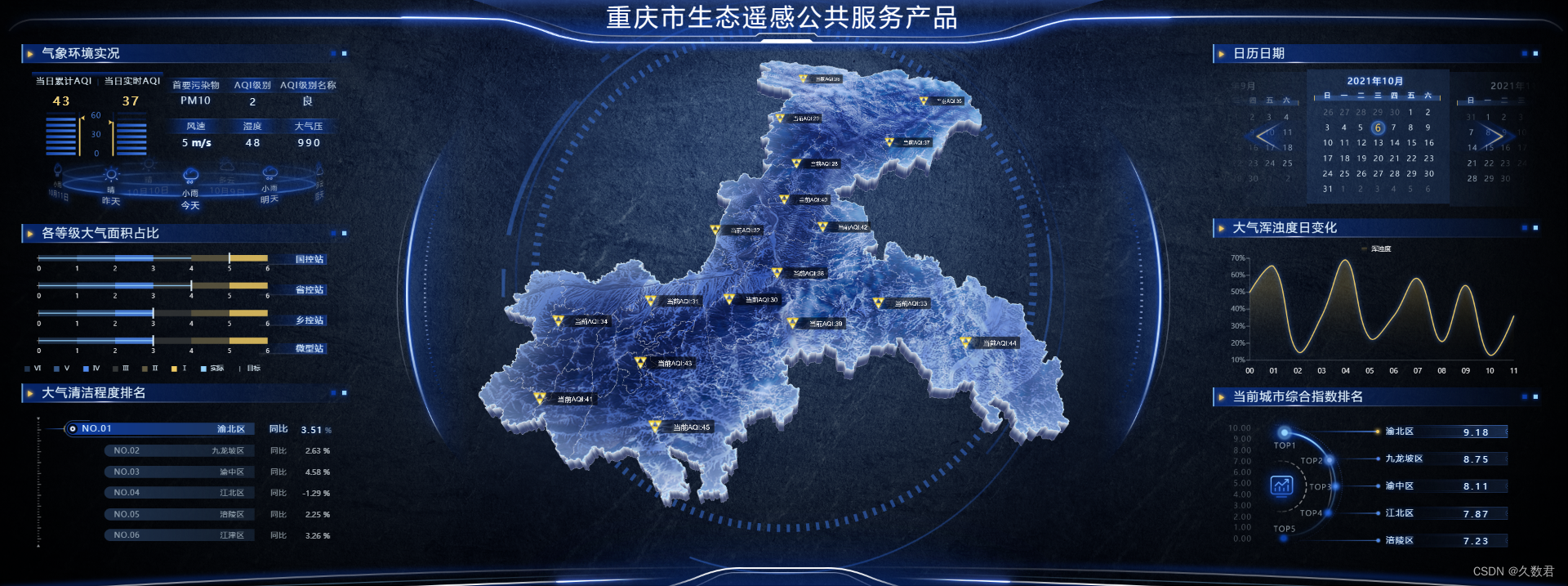
城市气象数据可视化:洞察气候变化,构建智慧城市
随着城市化进程的加速,城市气象数据的采集和分析变得越来越重要。气象数据不仅影响着人们的生活和出行,还与城市的发展和规划息息相关。在数字化时代,如何将城市中各个气象数据进行可视化,让复杂的数据变得简单易懂,成…...

Rust-IO
use std::io::Write; fn main() {/*std::io::stdin() 返回标准输入流stdin的句柄。read_line() stdin的句柄的一个方法,从标准输入流中读取一行数据返回一个Result枚举。会自动删除行尾的换行符\n。unwrap() 是一个帮助的方法,简化恢复错误的处理。返回R…...

cp -r 源目录 目标目录
在Linux中,要复制目录可以使用cp命令。cp命令用于复制文件和目录。要复制整个目录及其内容,可以使用 -r 或 --recursive 参数来递归地复制目录。以下是示例命令:bash cp -r 源目录 目标目录其中: 源目录是要复制的目录的路径。目…...
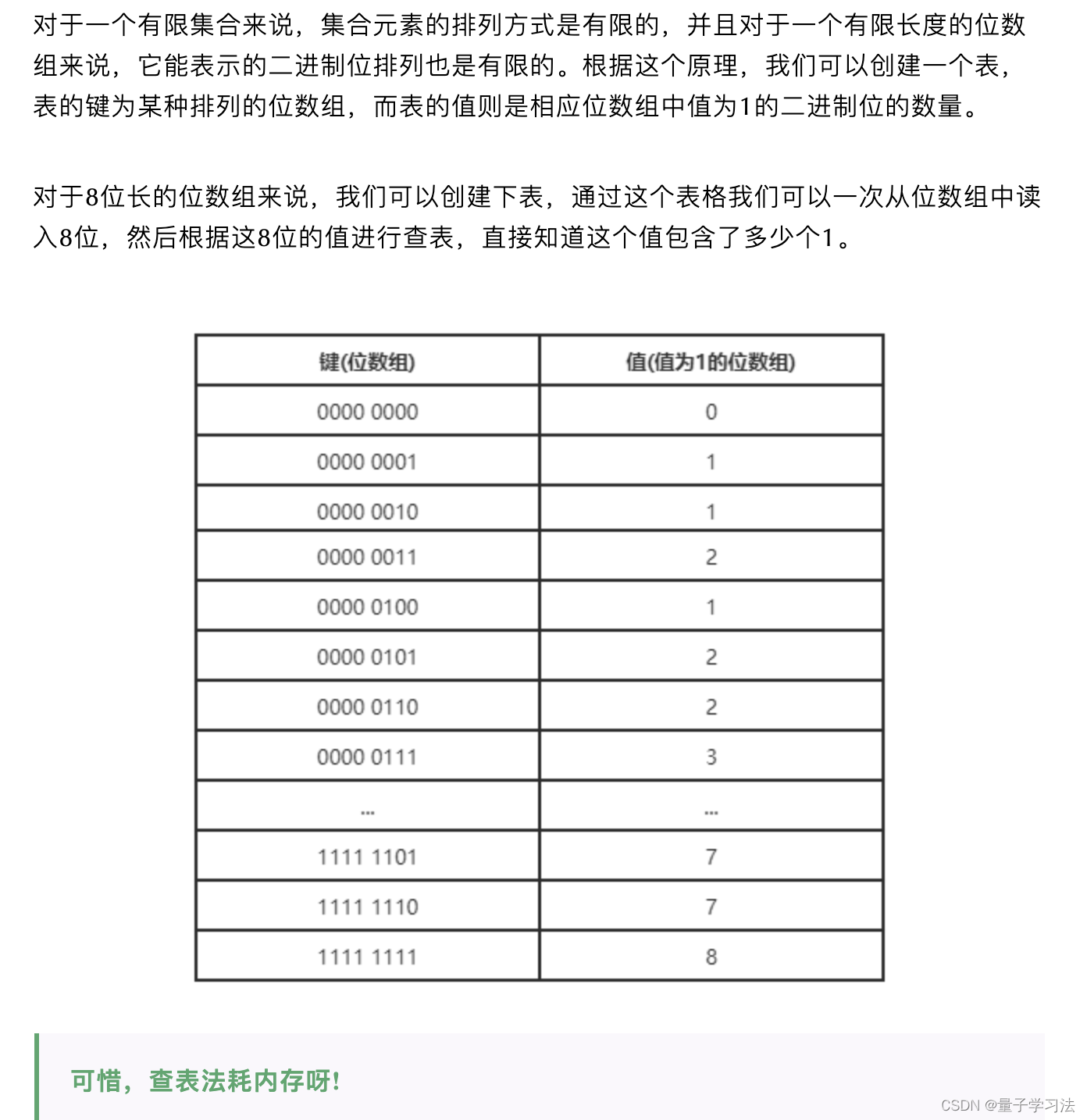
redis之Bitmap
位图数据结构其实并不是一个全新的玩意,我们可以简单的认为就是个数组,只是里面的内容只能为0或1而已(二进制位数组)。 GETBIT用于返回位数组在偏移量上的二进制位的值。值得我们注意的是,GETBIT的时间复杂度是O(1)。 GETBIT命令的执行过程如…...
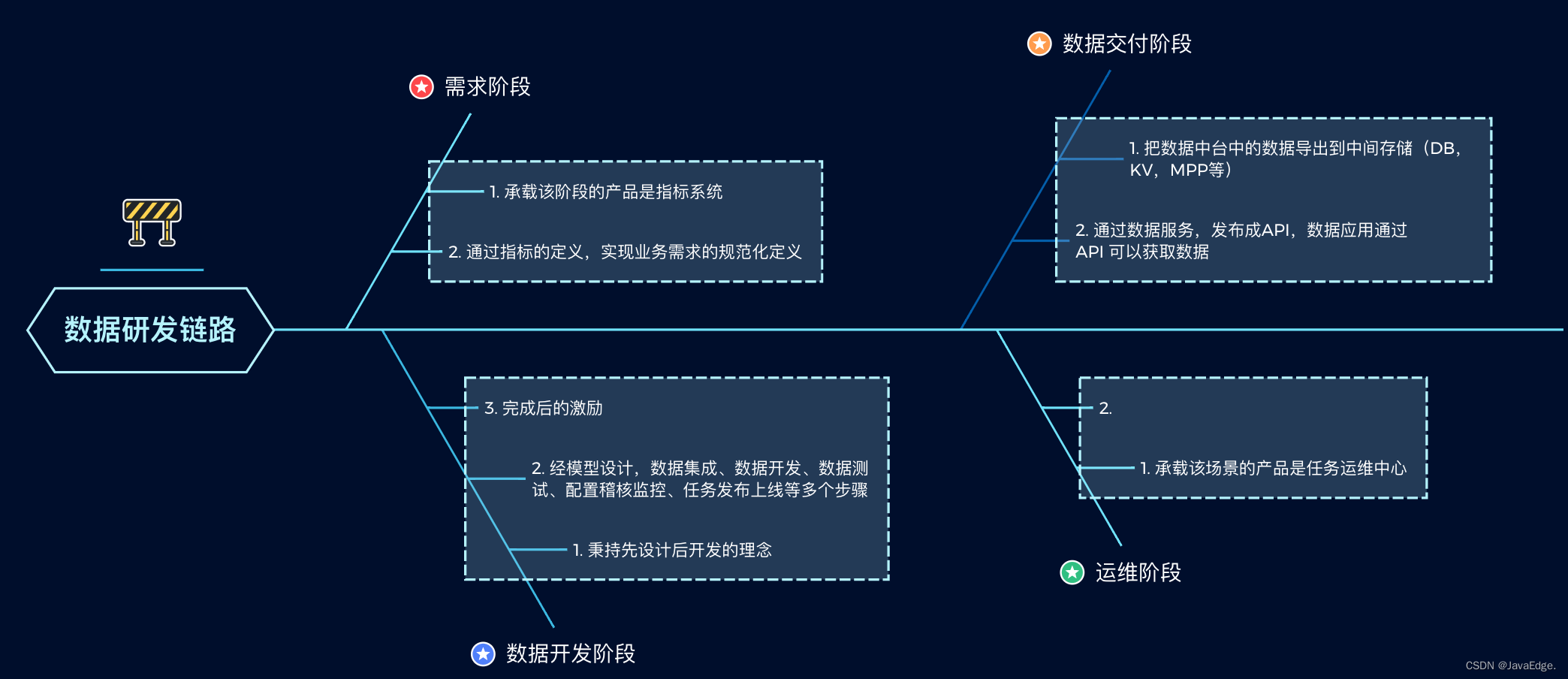
建设数据中台到底有啥用?
最近专注在数据和人工智能领域,从数据仓库、商业智能、主数据管理到大数据平台的建设,经过很多项目的沉淀和总结,最后我和团队一起总结了精益数据创新的体系。一直战斗在企业信息化一线。 企业为什么要建设数据中台,数据中台对于…...

[运维|系统] Centos设置本地编码
以下是在CentOS上更改系统编码的一般步骤: 使用locale命令查看当前的系统编码: locale如果需要更改系统编码,可以使用类似下面的命令来生成相应的locale设置(以UTF-8为例): sudo localedef -i en_US -f …...

深入探索Python中的os.listdir函数
深入探索Python中的os.listdir函数 1. 引言 在Python中,文件和目录操作是常见的任务之一。而os.listdir()函数是Python中用于获取指定目录下所有文件和子目录的函数之一。本篇博客将深入探索os.listdir()函数的用法和注意事项。 2. os模块简介 Python的os模块是…...
ROS1ROS2之CmakeList.txt和package.xml用法详解
前言:目前还在学习ROS无人机框架中,,, 更多更新文章详见我的个人博客主页【前往】 文章目录 1. CMakeLists.txt与package.xml的作用2. 生成CMakeLists.txt2.1 ROS12.2 ROS2 3. CMakeLists.txt编写3.1 ROS13.2 ROS2 4. package.xml…...

C#设计模式之---适配器模式
适配器模式(Adapter Pattern) 适配器模式(Adapter Pattern)也称包装样式或者包装(wrapper)。将一个类的接口转接成用户所期待的。适配器模式是一种结构型模式,一个适配使得因接口不兼容而不能在一起工作的类工作在一起…...

串口设备驱动
文章目录 一、串口简介二、Linux下串口驱动框架uart_driver 结构体uart_port 的添加与移除三、Linux下串口驱动工作流程四、Linux下串口应用开发终端工作模式多线程例程一、串口简介 串口全称叫做串行接口,通常也叫做 COM 接口,串行接口指的是数据一个一个的顺序传输,通信线…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
