数据结构--串、数组、广义表
这里写目录标题
- 串
- 定义
- 案例引用
- 串的类型定义以及存储结构
- 抽象类型定义
- 存储结构(顺序表较为常用)
- 顺序存储结构
- 链式存储结构
- 串的模式匹配算法(查找主串中是否有某个字串)
- BF算法
- KMP算法
- 设计思想
- 对字串的回溯进行了优化
- 代码
- 对next【j】进行优化
- 数组
- 类型
- 一维数组
- 二维数组
- 抽象类型定义
- 顺序存储结构
- 已知首元地址,求某个元素的地址(该元素第一个字节的地址)
- 特殊矩阵的压缩存储
- 对称矩阵
- 三角矩阵
- 带状矩阵
- 稀疏矩阵
- 顺序结构
- 链式结构
- 广义表
- 简介
- 性质
- 基本运算
- 案例
串
定义


也叫字符串


案例引用

串的类型定义以及存储结构
抽象类型定义


存储结构(顺序表较为常用)

顺序存储结构

为了方便一些操作,通常串的数组的第一个位置不放元素,而是从ch【1】开始存放元素
链式存储结构

如果一个结点的数据域只放一个字符,那么会导致存储密度异常的底,解决这个问题:在数据域放更多的字符数据

上面的结构体定义结点结构,下面定义链表结构
可以得知,对于好多功能的链式表示都是定义两个结构:一个是结点、一个是链表自己
定义链表时:先定义第二个结构体的对象,创建出链表,如果要创建新的结点,那么要用到第一个结构体,进行插入即可
串的模式匹配算法(查找主串中是否有某个字串)
BF算法



如果匹配失败,那么需要对两个串的下标进行回溯,从而重新比较下一组
对于主串,先回溯到原始位置:i=i-(j-1)
因为对于串的第一个下标都是1,所以,j移动的格数是j-1,而i与j同步移动,所以,回溯到原始位置是i-(j-1)
之后,因为要进行下一组比较,所以,i回到原始位置之后,还需要后移一位,所以i=i-(j-1)+1
对于字串,直接回到第一个位置即可:j=1

由于第一个位置下标为1,方便了这里字串位置的计算,直接i-T.length即可


while循换条件:当主串的下标或者字串的下标有一个出界,那就代表匹配结束,最后要么匹配成功(j>=T.length)要么匹配失败,循环继续的条件是二者都没有出界,一旦有一个出界,那么结果为假,那么整体为假,&&一假则假

最好情况是o(1)
最坏情况是o(n*m)
综合平均:o(n*m)
KMP算法
设计思想

对字串的回溯进行了优化


当字串第j个元素失配,需要回溯到的下标位置,放入数组next【j】中
第一个元素失配,那么需要回溯到0,但是由于没有0位置,所以实际上的操作是i++,j仍然是1
之后的元素 想看是否满足其前面的首位子集是否相等,例如j=5时,前四个元素,先看1、4,二者相等,所以k-1=1,那么k=2,之后再看12、34,再看123、234,如果有更大的k,那么就取最大的k为最终值,注意不能全部包含 例如1234,这样是不可以的
如果这种情况也不满足,就是其他情况,next【j】=1
代码
kmp算法:

next【j】的算法:

对next【j】进行优化



按照上述标黄的语句,进行分析即可,开头两位一般是01 或者00
之后 如果回溯位置的元素与自身相同,那么val值与回溯位置的next值一样,如果不同 ,那么仍然是自己的next值
最后要注意标黄的第四种情况,也就是如果相同,每次要判断到第一位为止
总结来说 不同为自身,相同做替换,不同则停止,相同则到底
改进后的next【j】:

数组
类型
一维数组

二维数组

二维数组可以是非线性结构,也可以是特殊的线性结构
特殊的线性结构:将一行看成一个线性结构,该行的每个元素是一个列向量

分开定义,实际上就是对特殊的线性结构的代码解释

数组一旦定义,那么长度固定,所以一般只是做取元素和修改元素操作
抽象类型定义


顺序存储结构

因为内存单元只能是线性的,但是数组有多维,所以要想办法将多维关系映射到一维关系,接下来通过找指定元素的地址来反映这个关系,接下来就是解决这个问题
已知首元地址,求某个元素的地址(该元素第一个字节的地址)
一维数组

二维数组





也就是(第一维下标*列数+第二维下标)*一个元素所占字节数+首元地址=目标元素的地址
(本质上,是要求该元素的前面有几个元素,但是因为下标都是从0开始,所以根据数学关系,下标的数就是该元素之前有几个元素的多少)
三维数组

n维

案例

注意这里假设元素占用一个空间,先利用第一个条件求出列数,之后利用公式,求出答案
特殊矩阵的压缩存储


对称矩阵

只存上三角或者下三角,元素位置:i*(i-1)/2+j 这就是目标元素前面的元素个数
三角矩阵

带状矩阵

稀疏矩阵
顺序结构


链式结构


每行每列都有许多头指针,负责该行或者该列
每个非零元素都有一个结点,该结点包括行数、列数、值、指向下方的结点、指向右方的结点,
广义表
简介


这里注意 表尾:1.是除了第一个元素之外的所有元素组成的表
2.一定是一个表,所以求表尾第一步:先写一个括号,之后看去掉表头之后,剩什么就直接填入括号里

例如 第二题 表头是第一个元素,第一个元素就是一个空括号 所以就是:()
表尾 先写一个空括号(),之后看除去表头之后 什么也没有了 就是空,所以 括号里什么都不写 所以还是()
第三题 表头:a
表尾:先写一个空括号,之后,将除去表头的剩下的元素填入空表中,也就是((b,c))
性质


基本运算

案例


循环m(模式串的长度)次,就可以将所有可能的情况都取得了
相关文章:

数据结构--串、数组、广义表
这里写目录标题 串定义案例引用串的类型定义以及存储结构抽象类型定义存储结构(顺序表较为常用)顺序存储结构链式存储结构 串的模式匹配算法(查找主串中是否有某个字串)BF算法KMP算法设计思想对字串的回溯进行了优化代码对next【j】进行优化 数组类型一维…...

白银挑战——链表高频面试算法题
算法通关村第一关–链表白银挑战笔记 开始时间:2023年7月18日14:39:36 链表 Java中定义一个链表 class ListNode {public int val;public ListNode next;ListNode(int x) {val x;next null;}}1、四种方法解决两个链表第一个公共子节点 解释一下什么是公共节点 如…...

海外腾讯云账号:腾讯云高性能计算平台 THPC
高性能计算平台(TencentCloud High Performance Computing,THPC)是一款腾讯云自研的高性能计算资源管理服务,集成腾讯云上的计算、存储、网络等产品资源,并整合 HPC 专用作业管理调度、集群管理等软件,向用…...
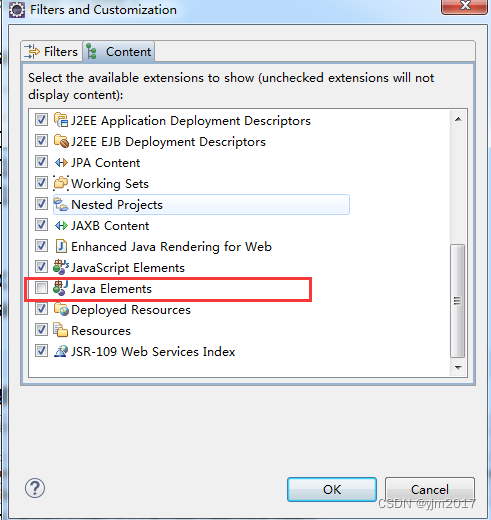
eclipse 最新版没有navigator视图如何解决
使用project exploere视图可以显示类似navigator视图 1.显示project exploere视图 window---->show view --->project exploere 2.project exploere视图转换为类似navigator视图 第一步:点击视图右上角三个点或者倒三角,点击fiters and custom…...
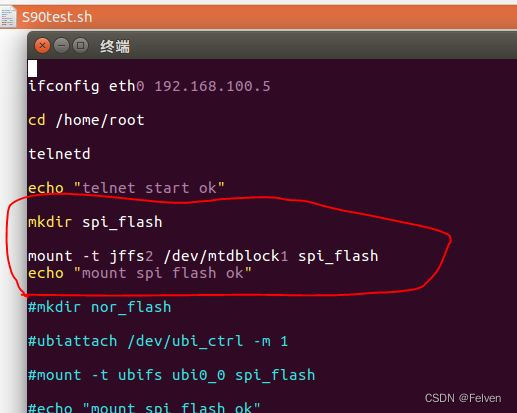
Zynq-Linux移植学习笔记之62- PL挂载复旦微flash
1、背景介绍 现在为了全国产化需要,之前所有的进口flash全部要换成国产flash 2、复旦微flash型号 其中EFM25QU256和EFM25QL256对标winbond的w25q256 nor flash 3、FPGA设置 复旦微flash只支持单线模式,当使用PL侧的IP核访问时,需要设置模式…...
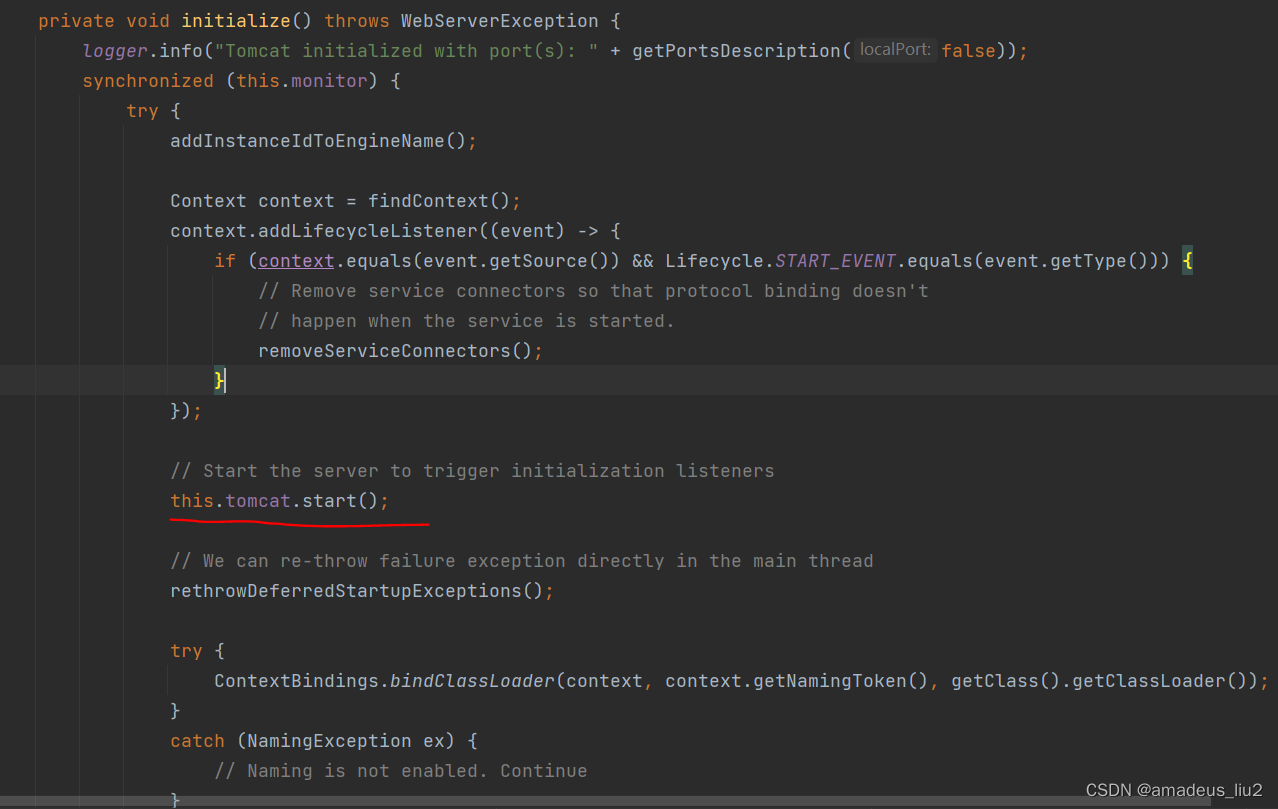
SpringBoot复习:(2)Tomcat容器是怎么启动的?
SpringApplication的run方法包含如下代码: 其中调用的refreshContext代码如下: 其中调用的refresh方法片段如下: 其中调用的refresh方法代码如下: 其中调用的super.refresh方法代码如下: public void refresh() th…...

1 MobileHomeTopicApplication
目录 1 OrderApplication 1.1 引用文件 1.2 #region 字段 1.3 #region 属性 OrderApplication 引用文件using System; using...
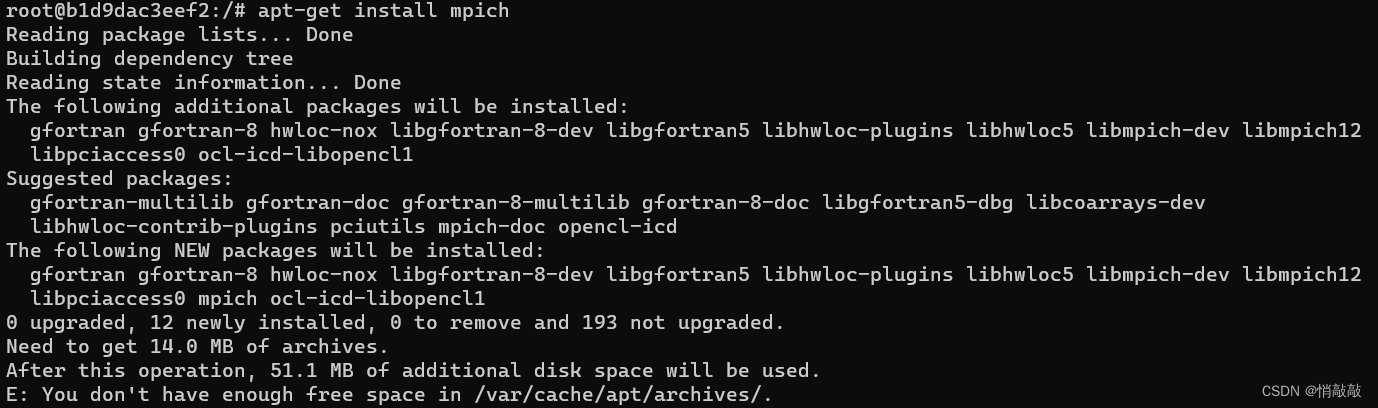
mpi4py包安装报错
报错情况 #include <mpi.h>^~~~~~~compilation terminated.failure.removing: _configtest.c _configtest.oerror: Cannot compile MPI programs. Check your configuration!!![end of output]note: This error originates from a subprocess, and is likely not a probl…...

C语言进阶-1
1、数据类型 1.1、基本数据类型 数据类型分2类:基本数据类型复合类型 基本类型:char short int long float double 复合类型:数组 结构体 共用体 类(C语言没有类,C有) 1.1.1、内存占用与sizeof运算符 数据…...

Python如何正确解决爬虫过程中的Cookie失效问题?
前言 本文是该专栏的第54篇,后面会持续分享python爬虫干货知识,记得关注。 在python爬虫项目中,Cookie是一种用于在客户端和服务器之间传递信息的技术。在爬取某些网站的时候,可能会需要登录才能正常获取到数据,这个时候就需要用到cookie来解决。通常情况下,需要将cooki…...

维护自己电脑浅析
作为一名计算机用户,维护自己的电脑是非常重要的,这可以保证电脑的正常运行、数据的安全、提高电脑的性能等。在本文中,我将分享一些我个人维护电脑的经验和技巧。 定期清理电脑 电脑在使用过程中会产生大量的临时文件、垃圾文件、缓存文件等…...
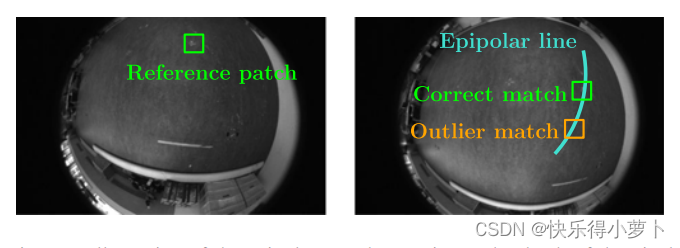
svo2论文
论文题目 SVO: Semidirect Visual Odometry for Monocular and Multicamera Systems 内容 1) 具有最小特征漂移的长特征轨迹; 2) 图像平面中的大量均匀分布的特征; 3)新特征与旧地标的可靠关联(即环路闭…...

【GoLang】MAC安装Go语言环境
小试牛刀 首先安装VScode软件 或者pycharmmac安装brew软件 brew install go 报了一个错误 不提供这个支持 重新brew install go 之后又重新brew reinstall go 使用go version 可以看到go 的版本 使用go env 可以看到go安装后的配置 配置一个环境变量 vim ~/.zshrc, # bre…...

epoll服务器创建
驱动 #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include <linux/io.h> #include <linux/device.h> #include <linux/uaccess.h> #include <linux/poll.h> unsigned int major; char kbuf[128]{0}…...

jdk11环境 提示“因为 accessExternalDTD 属性设置的限制导致不允许 ‘http‘ 访问“bug
在运行mybatis源码的时候,提示一下错误: Exception in thread "main" org.apache.ibatis.exceptions.PersistenceException: ### Error building SqlSession. ### Cause: org.apache.ibatis.builder.BuilderException: Error creating docum…...
Android Studio 的版本控制Git
Android Studio 的版本控制Git。 Git 是最流行的版本控制工具,本文介绍其在安卓开发环境Android Studio下的使用。 本文参考链接是:https://learntodroid.com/how-to-use-git-and-github-in-android-studio/ 一:Android Studio 中设置Git …...
一个 SpringBoot 项目能处理多少请求
首先,这个问题有坑,因为 spring boot 不处理请求,只是把现有的开源组件打包后进行了版本适配、预定义了一些开源组件的配置通过代码的方式进行自动装配进行简化开发。这是 spring boot 的价值。 使用 spring boot 进行开发相对于之前写配置文…...

Python中的r字符串前缀及其用法详解
Python中的r字符串前缀及其用法详解 1. 介绍 1.1 什么是r字符串前缀 在Python中,r字符串前缀是一种特殊的字符串前缀,用于表示原始字符串。当一个字符串以r前缀开始时,它将被视为原始字符串,其中的转义字符将被忽略。 1.2 r字…...
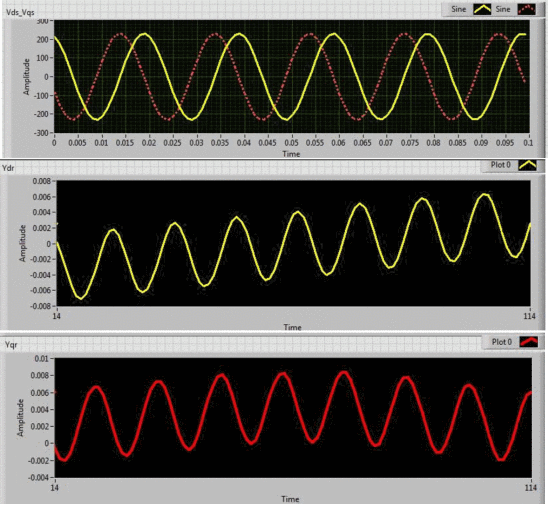
LabVIEW实现三相异步电机磁通模型
LabVIEW实现三相异步电机磁通模型 三相异步电动机由于经济和出色的机电坚固性而广泛用于工业化应用。这台机器的设计和驱动非常简单,但在控制扭矩和速度方面,它隐藏了相当大的功能复杂性。通过数学建模,可以理解机器动力学。 基于微分方程的…...

读书会-《影响力》
《影响力》这本书的作者罗伯特西奥迪尼时全球知名说服力研究权威。因其在影响力研究领域的开创性,人们将其称为“影响力研究领域的本杰明富兰克林”。这本书从人们的心理状态,进行了很多实验研究,总结出了7大规律。如果从事营销,需…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
