leetcode解题思路分析(一百四十五)1254 - 1266 题
- 统计封闭岛屿的数目
二维矩阵 grid 由 0 (土地)和 1 (水)组成。岛是由最大的4个方向连通的 0 组成的群,封闭岛是一个 完全 由1包围(左、上、右、下)的岛。请返回 封闭岛屿 的数目。
BFS或者DFS解题均可。
class Solution {
public:static constexpr int dir[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};int closedIsland(vector<vector<int>>& grid) {int m = grid.size();int n = grid[0].size();int ans = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] == 0) {queue<pair<int,int>> qu;grid[i][j] = 1;bool closed = true;qu.push(make_pair(i, j));while (!qu.empty()) {auto [cx, cy] = qu.front();qu.pop();if (cx == 0 || cy == 0 || cx == m - 1 || cy == n - 1) {closed = false;}for (int i = 0; i < 4; i++) {int nx = cx + dir[i][0];int ny = cy + dir[i][1];if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == 0) {grid[nx][ny] = 1;qu.emplace(nx, ny);}}}if (closed) {ans++;}}}}return ans;}
};- 得分最高的单词集合
你将会得到一份单词表 words,一个字母表 letters (可能会有重复字母),以及每个字母对应的得分情况表 score。请你帮忙计算玩家在单词拼写游戏中所能获得的「最高得分」:能够由 letters 里的字母拼写出的 任意 属于 words 单词子集中,分数最高的单词集合的得分。
状态压缩枚举单词,然后取计数最大的。
class Solution {
public:int maxScoreWords(vector<string>& words, vector<char>& letters, vector<int>& score) {int n = words.size(), res = 0;vector<int> count(26);for (auto c : letters) {count[c - 'a']++;}for (int s = 1; s < (1 << n); s++) {vector<int> wordCount(26); // 统计子集 s 所有单词的字母数目for (int k = 0; k < n; k++) {if ((s & (1 << k)) == 0) { // words[k] 不在子集 s 中continue;}for (auto c : words[k]) {wordCount[c - 'a']++;}}bool ok = true; // 判断子集 s 是否合法int sum = 0; // 保存子集 s 的得分for (int i = 0; i < 26; i++) {sum += score[i] * wordCount[i];ok = ok && (wordCount[i] <= count[i]);}if (ok) {res = max(res, sum);}}return res;}
};- 二维网格迁移
给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。请你返回 k 次迁移操作后最终得到的 二维网格。
展开为一维然后再重新排列即可。
class Solution {
public:vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {int m = grid.size(), n = grid[0].size();vector<vector<int>> ret(m, vector<int>(n));for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {int index1 = (i * n + j + k) % (m * n);ret[index1 / n][index1 % n] = grid[i][j];}}return ret;}
};- 在受污染的二叉树中查找元素
给出一个满足下述规则的二叉树.现在这个二叉树受到「污染」,所有的 treeNode.val 都变成了 -1。
请你先还原二叉树,然后实现 FindElements 类
很简单的题,DFS即可。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class FindElements {
private:unordered_set<int> s;void dfs(TreeNode* curr, int val){if (curr != nullptr){curr->val = val;s.insert(val);dfs(curr->left, 2*val + 1);dfs(curr->right, 2*val + 2);}}
public:FindElements(TreeNode* root) {dfs(root, 0);}bool find(int target) {return s.find(target) != s.end();}
};/*** Your FindElements object will be instantiated and called as such:* FindElements* obj = new FindElements(root);* bool param_1 = obj->find(target);*/- 可被三整除的最大和
给你一个整数数组 nums,请你找出并返回能被三整除的元素最大和。
可以用贪心算法解题:将数组分为Mod为0、1、2的三类,然后0的全取,1和2尽量取最多丢最少最小。也可以用动态规划解题,本题因为涉及到mod,所以动态规划中除了和前一个数i相关,还要和三种状态0/1/2相关。
class Solution {
public:int maxSumDivThree(vector<int>& nums) {vector<int> f = {0, INT_MIN, INT_MIN};for (int num: nums) {vector<int> g = f;for (int i = 0; i < 3; ++i) {g[(i + num % 3) % 3] = max(g[(i + num % 3) % 3], f[i] + num);}f = move(g);}return f[0];}
};- 推箱子
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。返回将箱子推到目标位置的最小 推动 次数,如果无法做到,请返回 -1。
BFS解题。
class Solution {
public:int minPushBox(vector<vector<char>>& grid) {int m = grid.size(), n = grid[0].size();int sx, sy, bx, by; // 玩家、箱子的初始位置for (int x = 0; x < m; x++) {for (int y = 0; y < n; y++) {if (grid[x][y] == 'S') {sx = x;sy = y;} else if (grid[x][y] == 'B') {bx = x;by = y;}}}auto ok = [&](int x, int y) -> bool { // 不越界且不在墙上return x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != '#';};vector<int> d = {0, -1, 0, 1, 0};vector<vector<int>> dp(m * n, vector<int>(m * n, INT_MAX));queue<pair<int, int>> q;dp[sx * n + sy][bx * n + by] = 0; // 初始状态的推动次数为 0q.push({sx * n + sy, bx * n + by});while (!q.empty()) {queue<pair<int, int>> q1;while (!q.empty()) {auto [s1, b1] = q.front();q.pop();int sx1 = s1 / n, sy1 = s1 % n, bx1 = b1 / n, by1 = b1 % n;if (grid[bx1][by1] == 'T') { // 箱子已被推到目标处return dp[s1][b1];}for (int i = 0; i < 4; i++) { // 玩家向四个方向移动到另一个状态int sx2 = sx1 + d[i], sy2 = sy1 + d[i + 1], s2 = sx2*n+sy2;if (!ok(sx2, sy2)) { // 玩家位置不合法continue;}if (bx1 == sx2 && by1 == sy2) { // 推动箱子int bx2 = bx1 + d[i], by2 = by1 + d[i + 1], b2 = bx2*n+by2;if (!ok(bx2, by2) || dp[s2][b2] <= dp[s1][b1] + 1) { // 箱子位置不合法 或 状态已访问continue;}dp[s2][b2] = dp[s1][b1] + 1;q1.push({s2, b2});} else {if (dp[s2][b1] <= dp[s1][b1]) { // 状态已访问continue;}dp[s2][b1] = dp[s1][b1];q.push({s2, b1});}}}q.swap(q1);}return -1;}
};- 访问所有点的最小时间
平面上有 n 个点,点的位置用整数坐标表示 points[i] = [xi, yi] 。请你计算访问所有这些点需要的 最小时间(以秒为单位)。
对于任意一种情况,从 x 移动到 y 的最少次数为 dx 和 dy 中的较大值 max(dx, dy),这也被称作 x 和 y 之间的 切比雪夫距离。
class Solution {
public:int minTimeToVisitAllPoints(vector<vector<int>>& points) {int x0 = points[0][0], x1 = points[0][1];int ans = 0;for (int i = 1; i < points.size(); ++i) {int y0 = points[i][0], y1 = points[i][1];ans += max(abs(x0 - y0), abs(x1 - y1));x0 = y0;x1 = y1;}return ans;}
};相关文章:
1254 - 1266 题)
leetcode解题思路分析(一百四十五)1254 - 1266 题
统计封闭岛屿的数目 二维矩阵 grid 由 0 (土地)和 1 (水)组成。岛是由最大的4个方向连通的 0 组成的群,封闭岛是一个 完全 由1包围(左、上、右、下)的岛。请返回 封闭岛屿 的数目。 BFS或者DFS…...

使用 GORM 连接数据库并实现增删改查操作
步骤 1:安装 GORM 首先,我们需要安装 GORM 包。在终端中运行以下命令: shell go get -u gorm.io/gorm 步骤 2:导入所需的包 在 Go 代码的开头导入以下包: import ("gorm.io/driver/mysql" // 如果你使用…...

kafka集群搭建(Linux环境)
zookeeper搭建,可以搭建集群,也可以单机(本地学习,没必要搭建zookeeper集群,单机完全够用了,主要学习的是kafka) 1. 首先官网下载zookeeper:Apache ZooKeeper 2. 下载好之后上传到…...
树莓派本地快速搭建web服务器,并发布公网访问
文章目录 树莓派本地快速搭建web服务器,并发布公网访问 树莓派本地快速搭建web服务器,并发布公网访问 随着科技的发展,电子工业也在不断进步,我们身边的电子设备也在朝着小型化和多功能化演进,以往体积庞大的电脑也在…...

集合中的数据结构
栈 先进后出入口跟出口在同一侧 队列 先进先出入口跟出口在不同的一层 数组 查询快、增删慢查询快是因为数组的地址是连续的,我们通过数组的首地址就可以找到数组,之后通过数组的下标就可以访问数组的每一个元素。增删慢是因为数组的长度是固定的&…...
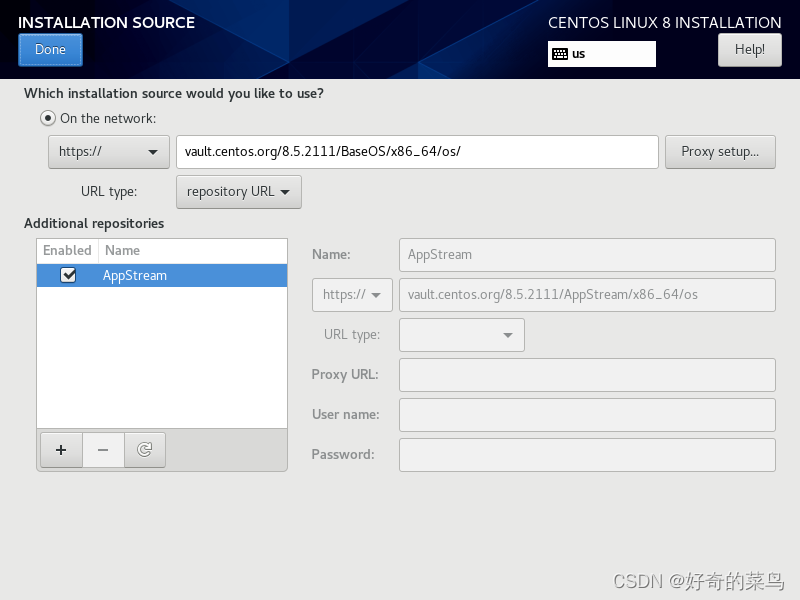
CentOS 8 错误: Error setting up base repository
配置ip、掩码、网关、DNS VMware网关可通过如下查看 打开网络连接 配置镜像的地址 vault.centos.org/8.5.2111/BaseOS/x86_64/os/...

java外观模式
在Java中,外观模式(Facade Design Pattern)用于为复杂的子系统提供一个简单的接口,以方便客户端的使用。外观模式是一种结构型设计模式,它隐藏了系统的复杂性,将多个类的复杂操作封装在一个外观类中&#x…...
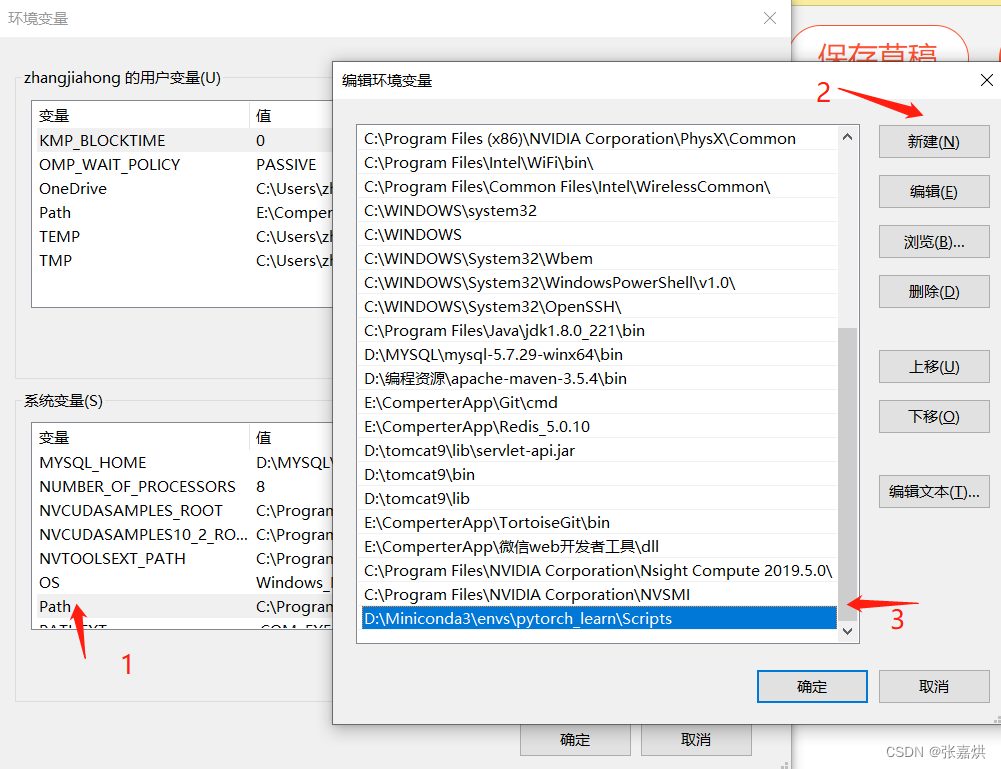
3秒快速打开 jupyter notebook
利用 bat 脚本,实现一键打开 minconda 特点: 1、可指定 python 环境 2、可指定 jupyter 目录 一、配置环境 minconda 可以搭建不同的 python 环境,所以我们需要找到 minconda 安装目录,把对应目录添加到电脑环境 PATH 中&#…...
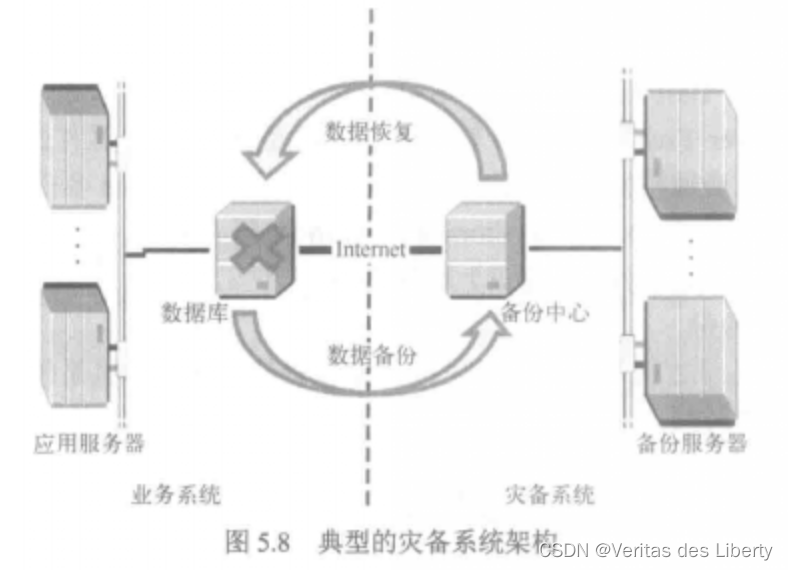
数据安全
数据的备份与恢复 1. 数据备份技术 任何数据在长期使用过程中,都存在一定的安全隐患。由于认为操作失误或系统故障,例如认为错误、程序出错、计算机失效、灾难和偷窃,经常造成数据丢失,给个人和企业造成灾难性的影响。在这种情况…...
华为nat64配置
1.前期环境准备 环境拓扑 拓扑分为两个区域,左边为trust区域,使用IPv4地址互访,右边为untrust区域,使用IPv6地址互访 2.接口地址配置 pc1地址配置 pc2地址配置 FW接口配置 (1)首先进入防火墙配置界面 注:防火墙初始账号密码为user:admin,pwd:Admin@123,进入之后…...

从分片传输到并行传输之大文件传输加速技术
随着大文件的传输需求越来越多,传输过程中也会遇到很多困难,比如传输速度慢、文件安全性低等。为了克服这些困难,探讨各种大文件传输加速技术。其中,分片传输和并行传输是两种比较常见的技术,下面将对它们进行详细说明…...
mybatisPlus入门篇
文章目录 初窥门径1.1 初识MybatisPlus1.2 MybatisPlus的特性1.3 MybatisPlus的架构模型 入门案例2.1 准备相关开发环境2.2 搭建springboot工程2.3 创建数据库2.4 引入相关依赖2.5 创建实体类2.6 集成MybatisPlus2.7 单元测试2.8 springboot日志优化 初窥门径 1.1 初识Mybatis…...
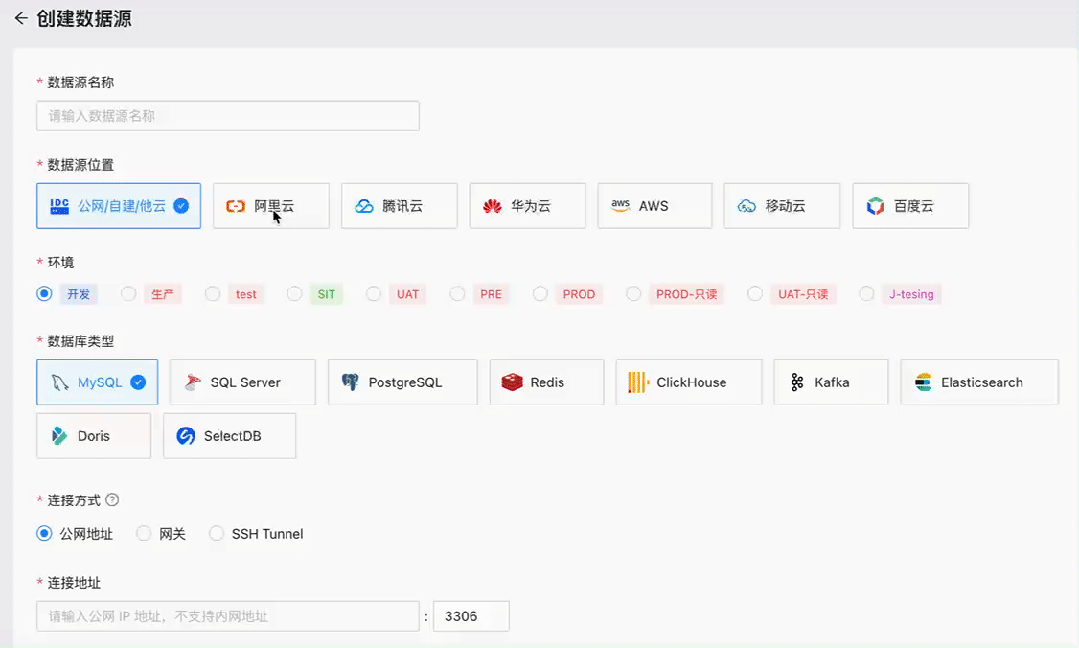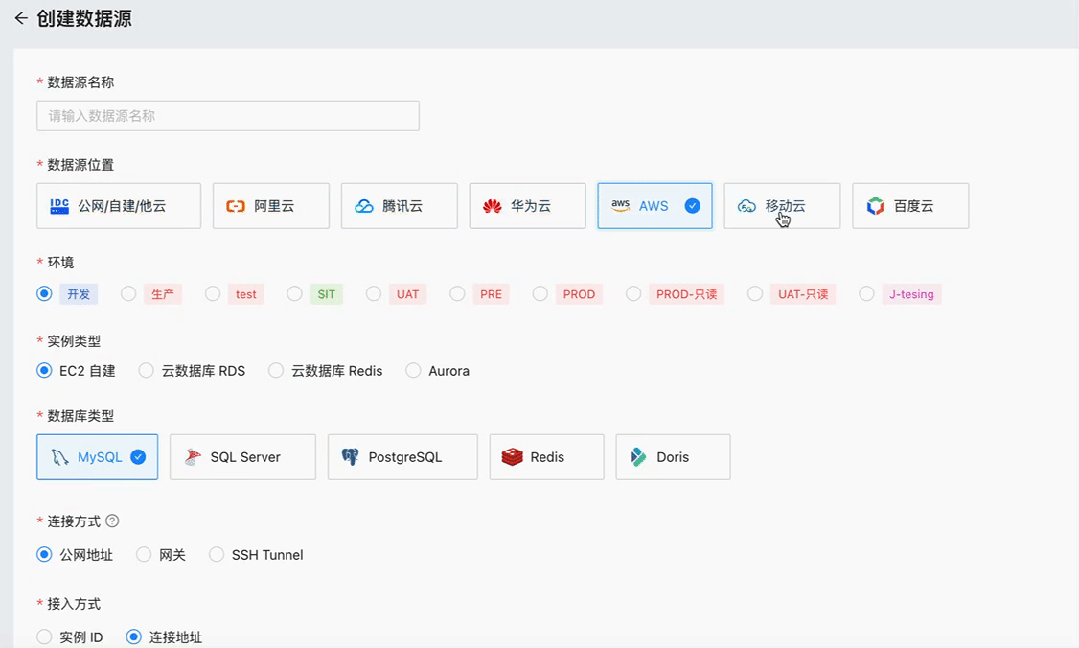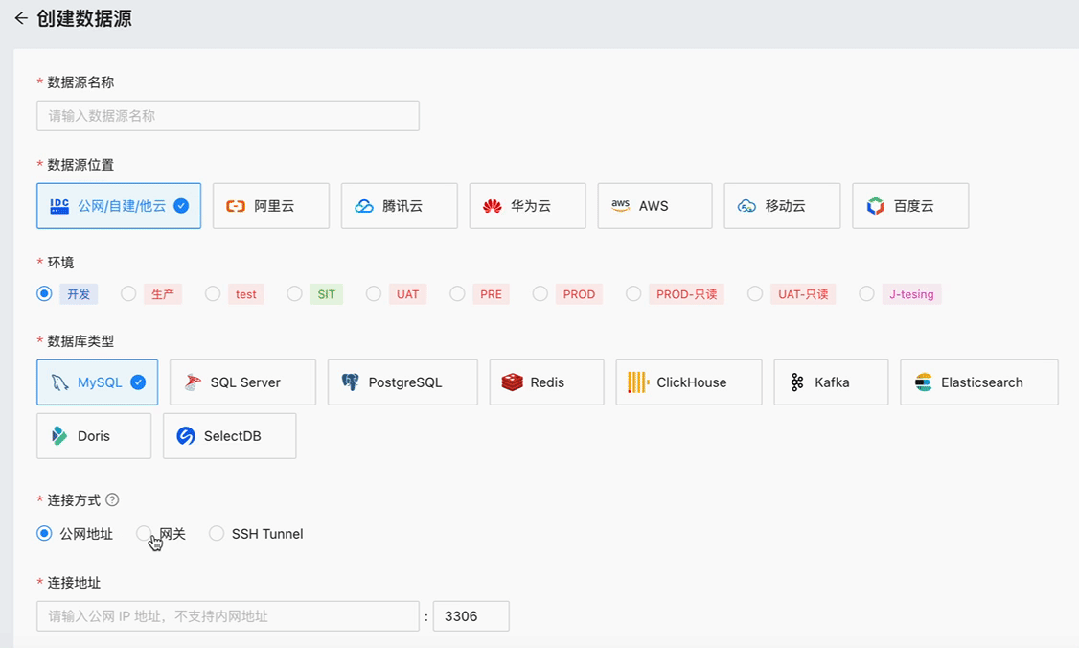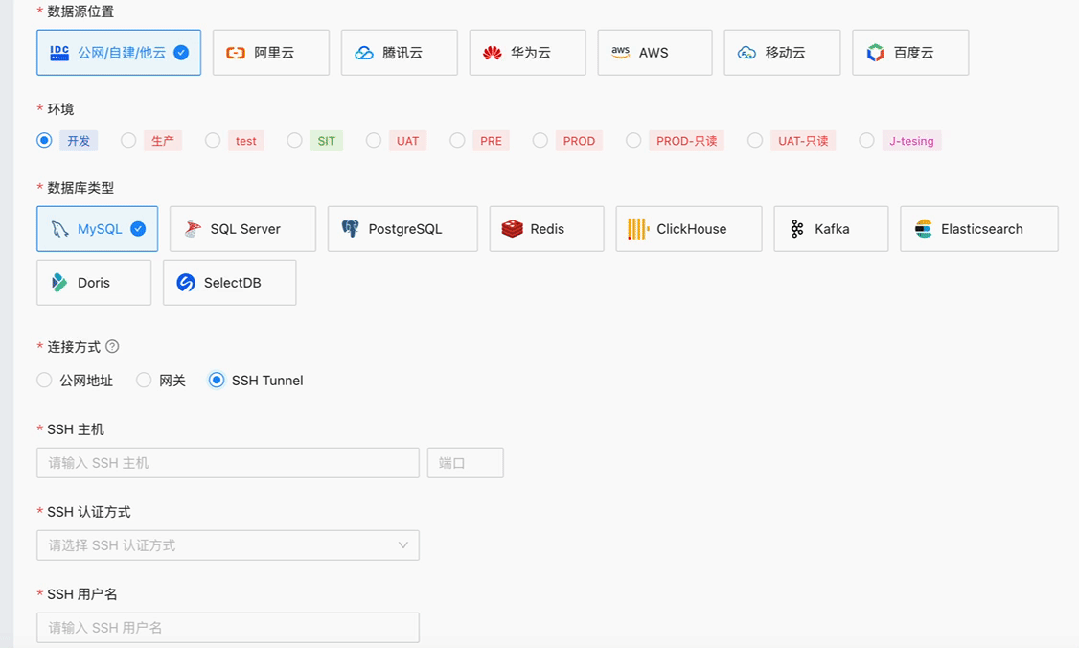
NineData支持最受欢迎数据库PostgreSQL
根据在 Stack Overflow 发布的 2023 开发者调研报告中显示,PostgreSQL 以 45% vs 41% 的受欢迎比率战胜 MySQL,成为新的最受欢迎的数据库。NineData 也在近期支持了 PostgreSQL,用户可以在 NineData 平台上进行创建数据库/Schema、管理用户与…...

Redis配置类
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

【前端知识】React 基础巩固(三十六)——RTK中的异步操作
React 基础巩固(三十六)——RTK中的异步操作 一、RTK中使用异步操作 引入RTK中的createAsyncThunk,在extraReducers中监听执行状态 import { createSlice, createAsyncThunk } from "reduxjs/toolkit"; import axios from "axios";export cons…...

33. 本地记事本
本地记事本 html部分 <button class"add"><i class"iconfont icon-jiahao"></i> </button>css部分 *{margin: 0;padding: 0; } body{background-color: #7bdaf3;display: flex;padding-top: 3rem;flex-wrap: wrap; } .add{pos…...
Android Glide预处理preload原始图片到成品resource 预加载RecyclerViewPreloader,Kotlin
Android Glide预处理preload原始图片到成品resource & 预加载RecyclerViewPreloader,Kotlin <uses-permission android:name"android.permission.READ_EXTERNAL_STORAGE" /><uses-permission android:name"android.permission.READ_MED…...

亚马逊云科技全新Amazon Bedrock,助力客户构建生成式AI应用
亚马逊云科技近日在纽约峰会上宣布全面扩展其全托管基础模型服务Amazon Bedrock,包括新增Cohere作为基础模型供应商,加入Anthropic和Stability AI的最新基础模型,并发布变革性的新功能Amazon Bedrock Agents功能。客户无需管理任何基础设施&a…...

题解:ABC275 C-Counting Squares
题解:ABC275 C-Counting Squares 题目 链接:Atcoder。 链接:洛谷。 难度 算法难度:入门。 思维难度:普及。 调码难度:普及。 综合评价:简单。 算法 dfs数论。 思路 由数学方法可严谨…...
加载已训练好的目标检测YOLOv8,v5,v3,v6模型,对数据集中某张图片中的object打上方框、标出类别,并将图片保存到本地
参考的教程:Python - Ultralytics YOLOv8 Docs 在与ultralytics代码同一层级下新建 predict.py 里面写下面的内容。运行即可 from ultralytics import YOLO from PIL import Image import cv2# 加载计划使用的模型 model YOLO("yolov8n.pt") # load a…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
