线段树详解 原理解释 + 构建步骤 + 代码(带模板)
目录
介绍:
定义:
以具体一个题目为例:
树的表示方法:
实现步骤:
构建结点属性:
pushup函数:
build函数:
pushdown函数:
modify函数:
query函数:
如何记忆:
模板:
介绍:
线段树(Segment Tree)是一种常用的数据结构,用于解决涉及区间查询的问题。它主要用于在数组或列表等数据结构上支持以下两类查询操作:
- 区间查询:查询某个区间内的统计信息,例如求和、最大值、最小值等。
- 区间更新:修改数组中某个区间元素的值,并相应地更新线段树中的信息。
核心思想是将原始数据递归地划分成一系列不相交的区间,并在每个区间上维护一些预先计算好的信息,以支持高效的区间查询。
定义:
假设我们有一个包含 N 个元素的数组 A,线段树 T 是基于数组 A 的线段树。线段树 T 是一个满二叉树,它具有以下性质:
- 根节点表示整个数组的区间 [1, N]。
- 如果一个节点表示的区间是 [left, right],则它的左子节点表示的区间是 [left, mid],右子节点表示的区间是 [mid+1, right],其中 mid 是 left 和 right 的中间值。
- 叶子节点表示数组 A 中的单个元素,而内部节点表示对应区间上的预计算信息(如区间和、区间最大值等)。
- 线段树通常使用数组来模拟实现。
线段树算法一般包含以下五个函数:
1.build(); 初始构建一个线段树。
2.pushpu(); 向上传递信息。
3.pushdown(); 向下传递懒标记,并且更新子树。
4.modify(); 修改某一区间。
5.query(); 查询某一区间信息。
下面我们一个一个来介绍。
以具体一个题目为例:
下面解析以此题目为例子。
树的表示方法:
我们用 tr 数组来模拟这颗树。
假设根节点在 tr 数组中的的下标为为 i,那么其左右子树的下标为:
左:i * 2 (i << 1)
右:i * 2 + 1 (i << 1 | 1)
我们一般使用位运算,也就是括号里的,含义是一样的。所以可以计算出,tr 数组的长度最多就是题目所给数组长度的4倍。
实现步骤:
事先把输入的数组存在 w数组 中。
构建结点属性:
树结点其实就是一个区间,所以属性包含:左右边界,懒标记。
此题的懒标记就是区间需要加上的值 d 。
根据题目我们还需要查询区间的元素和,所以在其中添加一个 sum。
struct Node
{int l, r;LL sum;LL add; // 懒标记
}tr[N * 4];;pushup函数:
我们在 build 一颗树之前,要先写 pushup 函数,用于向上传递信息,因为我们只知道叶子结点的值,我们要用后序遍历去构建父亲,所以要用到 pushup ,根据题目,我们要向上传递的信息显然是左右子树的 sum 和,这样就可以算出父亲的 sum 。
void pushup(int u) // 向上传递信息
{tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}build函数:
接下来我们开始构建这颗树,若区间内只有一个元素(l == r),说明我们找到了叶子结点,给叶子结点赋值,若不是结子节点(l != r),就继续向左右子树递归,在递归完成时(后序遍历)使用pushup,通过已经获得值的子树去更新父亲。
void build(int u, int l, int r)
{if (l == r) tr[u] = {l, r, w[l], 0}; // 叶子节点else{tr[u] = {l, r};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); // 若不是叶子节点,向下递归pushup(u); // 通过子树构建父亲}
}pushdown函数:
pushdown函数是给子树传递懒标记的,如果懒标记不为空,就将父亲的懒标记传递给左右子树,并且通过懒标记更新左右子树的信息,此题求的是sum,所以子树的 sum 值就要加上区间长度乘上父亲的懒标记,最后清空父亲的懒标记。
注意:懒标记表示的子树需要添加的信息,不包含父亲自己,所以在传递懒标记时,才要传递懒标记同时更新子树。
void pushdown(int u)
{auto &root = tr[u], &left = tr[u << 1], & right = tr[u << 1 | 1];if (root.add){// 传递懒标记并且更新子树left.add += root.add, left.sum += (LL)(left.r - left.l + 1) * root.add;right.add += root.add, right.sum += (LL)(right.r - right.l + 1) * root.add;root.add = 0; // 删除懒标记}
}modify函数:
修改区间信息,如果当前遍历的结点区间已经在区间中,那么就直接给其加上懒标记,并且计算更新其 sum。如果当前遍历的结点区间中的一部分是需要修改的区间,那么就先向下传递懒标记pushdown,然后在向需要修改的左右子树去递归,后序返回时,要给更新父亲pushup。
void modify(int u, int l, int r, int v)
{// 结点在要修改的区间中if (l <= tr[u].l && r >= tr[u].r){tr[u].sum += (tr[u].r - tr[u].l + 1) * v;tr[u].add += v; // 加上懒标记}else{pushdown(u); // 先传递懒标记int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) modify(u << 1, l, r, v);if (r > mid) modify(u << 1 | 1, l, r, v);pushup(u); // 更新父亲}
}query函数:
用于查询区间信息,这里就是查询区间的sum。若遍历到的结点区间在查询区间之中,就返回其sum,若结点区间只有一部分在查询区间中,一样的,也是先传递懒标记,然后继续向需要计算的左右子树去递归,后序返回时计算结果。
LL query(int u, int l, int r)
{if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum; // 返回区间信息pushdown(u); // 也是先传递懒标记LL v = 0;int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) v = query(u << 1, l, r);if (r > mid) v += query(u << 1 | 1, l, r);return v;
}如何记忆:
最重要的是注意每个函数pushup,pushdown函数的位置。只有在modify函数才两个一起用。
build函数只用一个pushup,query函数只用一个pushdown。
模板:
根据具体题目,自行修改。
// 操作是给区间每一个数加d
// 询问是求某一区间和
#include<iostream>using namespace std;typedef long long LL;
const int N = 100010;int w[N];
int n, m;struct Node
{int l, r;LL sum;LL add; // 懒标记
}tr[N * 4];;void pushup(int u) // 向上传递信息
{tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{auto &root = tr[u], &left = tr[u << 1], & right = tr[u << 1 | 1];if (root.add){// 传递懒标记并且更新子树left.add += root.add, left.sum += (LL)(left.r - left.l + 1) * root.add;right.add += root.add, right.sum += (LL)(right.r - right.l + 1) * root.add;root.add = 0; // 删除懒标记}
}
void build(int u, int l, int r)
{if (l == r) tr[u] = {l, r, w[l], 0}; // 叶子节点else{tr[u] = {l, r};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); // 若不是叶子节点,向下递归pushup(u); // 通过子树构建父亲}
}
void modify(int u, int l, int r, int v)
{// 结点在要修改的区间中if (l <= tr[u].l && r >= tr[u].r){tr[u].sum += (tr[u].r - tr[u].l + 1) * v;tr[u].add += v; // 加上懒标记}else{pushdown(u); // 先传递懒标记int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) modify(u << 1, l, r, v);if (r > mid) modify(u << 1 | 1, l, r, v);pushup(u); // 更新父亲}
}LL query(int u, int l, int r)
{if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum; // 返回区间信息pushdown(u); // 也是先传递懒标记LL v = 0;int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) v = query(u << 1, l, r);if (r > mid) v += query(u << 1 | 1, l, r);return v;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++i) scanf("%d", &w[i]); // 读入数组build(1, 1, n); // 以1为根节点,1~n区间建树char op[2];int l, r, t;// 读入修改和查询,q是查询,否则是修改while (m -- ){scanf("%s%d%d", op, &l, &r);if (*op == 'Q') printf("%lld\n", query(1, l, r));else{scanf("%d", &t);modify(1, l, r, t);}}return 0;
}相关文章:

线段树详解 原理解释 + 构建步骤 + 代码(带模板)
目录 介绍: 定义: 以具体一个题目为例: 树的表示方法: 实现步骤: 构建结点属性: pushup函数: build函数: pushdown函数: modify函数: query…...

Java中Timer的使用
Timer 简述 在Java中,Timer(计时器)是一个用于安排定时任务的类。它可以实现在指定的时间间隔或指定的时间点执行某项任务或操作。 简单的来说Timer就是在Java中用来实现定时任务的工具。 Timer的API Timer中有两API可以使用分别是schedule…...

关于EJB,这两文把热闹和门道都说清楚了
关于技术的很多概念,如果你是小白,不建议看官网。原因就在于官网描述太抽象,就像八股文,看完感觉好像说了很多,但回过头又感觉似乎啥都没说。太虚、不接地气,是最大毛病。其实这些官网的打太极式的表述&…...

MixFormerV2: Efficient Fully Transformer Tracking
摘要 基于变压器的跟踪器在标准基准测试上取得了很强的精度。然而,它们的效率仍然是在GPU和CPU平台上实际部署的一个障碍。在本文中,为了克服这一问题,我们提出了一个完全变压器跟踪框架,称为MixFormerV2,没有任何密集…...
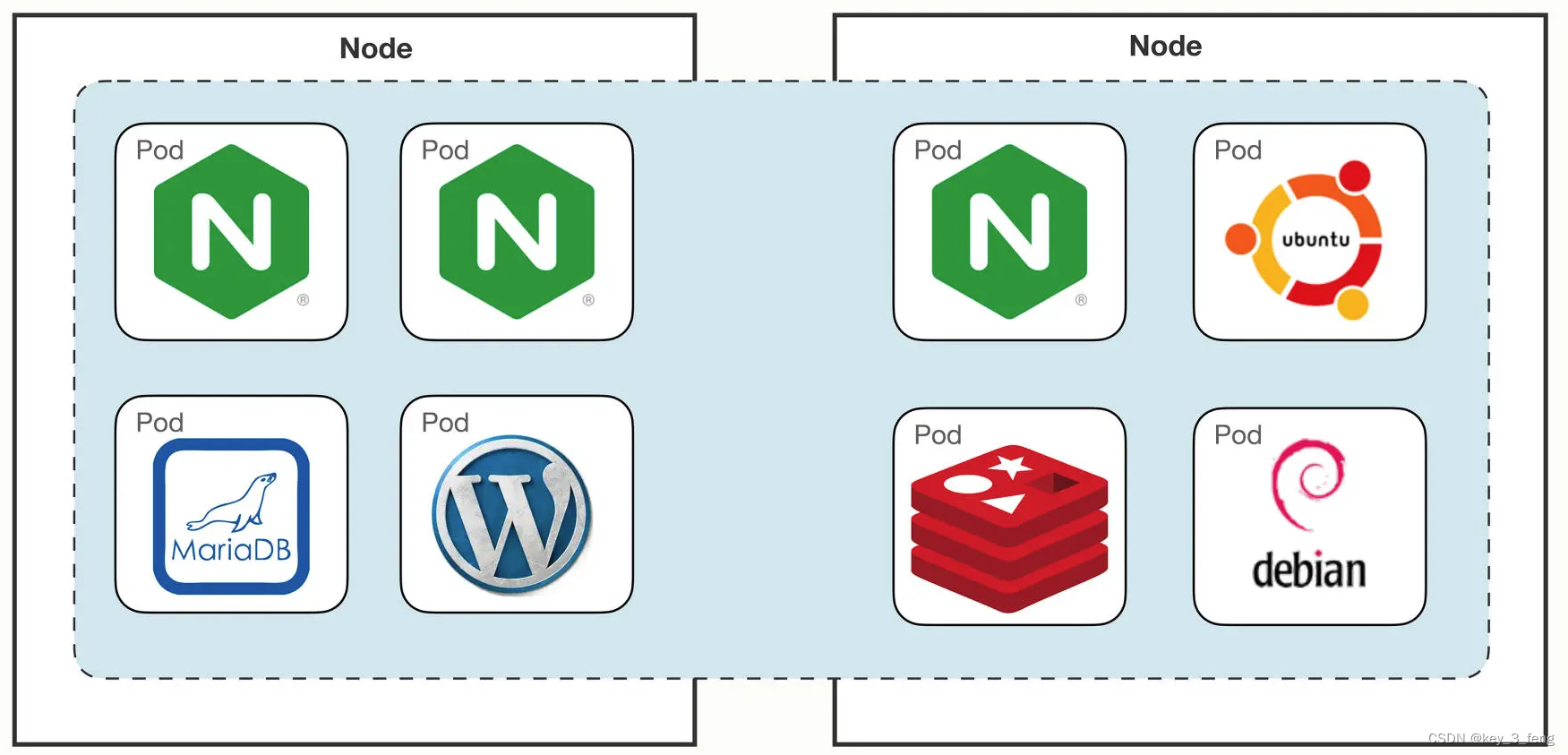
K8S中网络如何通信
Kubernetes 提出了一个自己的网络模型“IP-per-pod”,能够很好地适应集群系统的网络需求,它有下面的这 4 点基本假设: 集群里的每个 Pod 都会有唯一的一个 IP 地址。Pod 里的所有容器共享这个 IP 地址。集群里的所有 Pod 都属于同一个网段。…...
)
LangChain Agents深入剖析及源码解密上(三)
AutoGPT案例V1版本 AutoGPT是一个实验性的开源应用程序,展示了GPT-4语言模型的功能,AutoGPT程序由GPT-4驱动,将大语言模型的思考链接在一起,以自主实现设定的任何目标。作为GPT-4完全自主运行的首批例子之一,AutoGPT突破了人工智能的可能性。LangChain框架复现了https://g…...
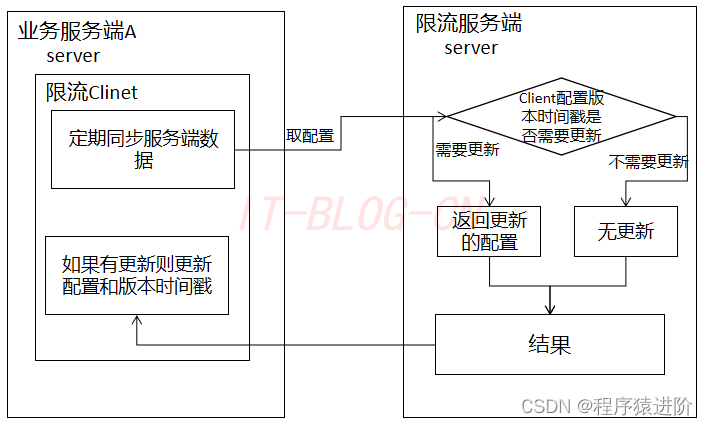
分布式限流方案及实现
优质博文:IT-BLOG-CN 一、限流的作用和意义 限流是对高并发访问进行限制,限速的过程。通过限流来限制资源,可以提高系统的稳定性和可靠性,控制系统的负载,削峰填谷,保证服务质量。 服务限流后的常见处理…...
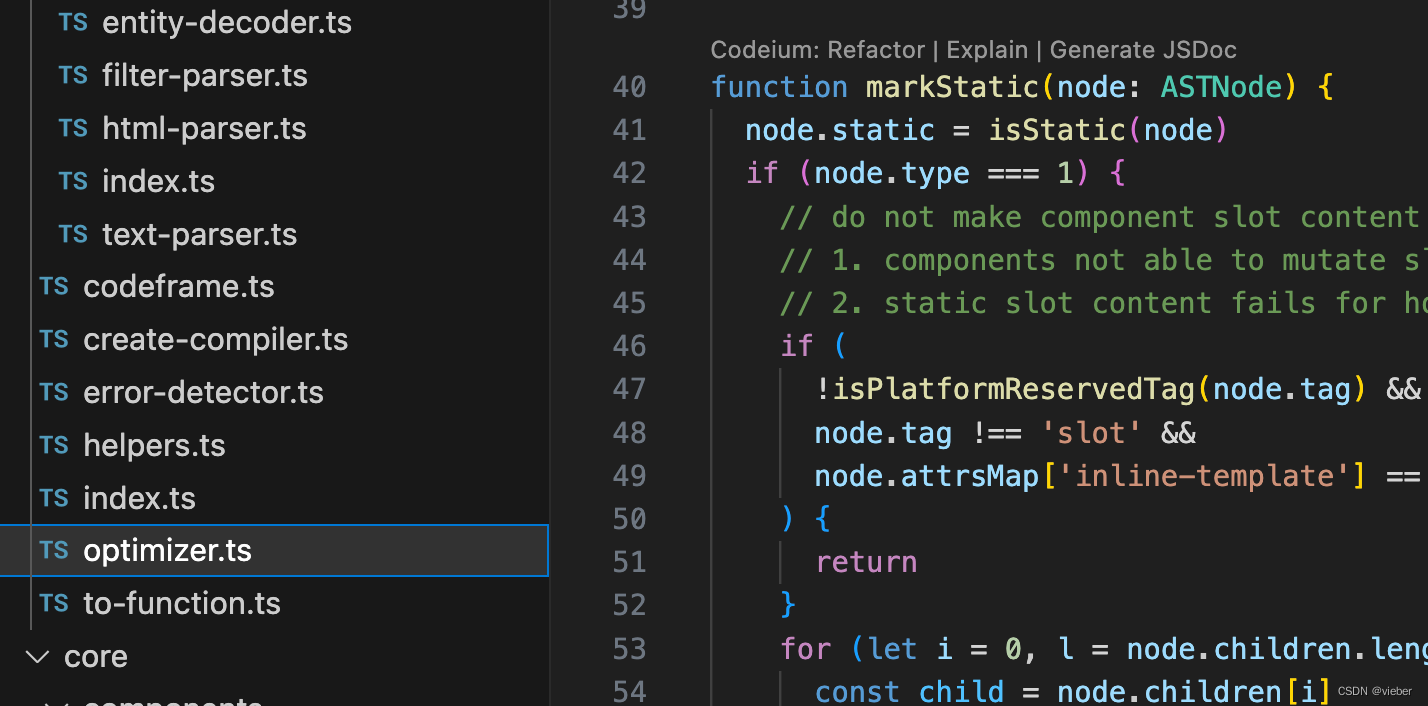
vuejs源码阅读之优化器
前面讲过vuejs中解析器是把html模版解析成AST,而优化器的作用是在AST中找到静态子树并打上标记。 静态子树是指的那些在AST中永远不会发生变化的节点。 例如,一个纯文本节点就是静态子树,而带变量的文本节点就不是静态子树,因为…...

【C++】-动态内存管理
作者:小树苗渴望变成参天大树 作者宣言:认真写好每一篇博客 作者gitee:gitee 如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点 点 关 注 吧! 文章目录 前言一、C内存管理方式1.1 new/delete操作内置类型 总结 前言 今天再讲一个…...

微服务SpringCloud教程——微服务是什么
微服务(MicroServices)最初是由 Martin Fowler 于 2014 年发表的论文《MicroServices》中提出的名词,它一经提出就成为了技术圈的热门话题。 微服务,我们可以从字面上去理解,即“微小的服务”,下面我们从“…...
RNN架构解析——LSTM模型
目录 LSTMLSTM内部结构图 Bi-LSTM实现 优点和缺点 LSTM LSTM内部结构图 Bi-LSTM 实现 优点和缺点...

苹果电脑系统优化工具:Ventura Cache Cleaner for mac
Ventura Cache Cleaner for Mac是一款专门为苹果电脑开发的系统优化工具,旨在帮助用户清理和优化Mac电脑,提高系统性能和速度。该软件由美国公司Northern Softworks开发,已经推出了多个版本,适用于不同版本的Mac操作系统。 Ventu…...

为了爱人穿越沙漠-心理测试
我觉得很准的一个心理测试。我的答案反射出我的态度,它们是100%的贴切。有兴趣的朋友也不妨一试。 你有一个深爱着的心上人,然而你们却被一片无垠的沙漠相隔两地,你禁不住思念的折磨,决定穿越沙漠去寻找你心中的那个爱人…… 1、…...
SpringBoot月度员工绩效考核管理系统【附任务书|ppt|万字文档(LW)和搭建文档】
主要功能 员工登录: ①首页、个人中心:修改密码、个人信息管理等 ②公告信息管理、绩效指标管理、绩效考核管理 管理员登录: ①首页、个人中心:修改密码、个人信息管理等 ②公告信息管理、部门管理、岗位管理、员工管理、绩效指标…...

【新星计划】STM32F103C8T6 - C语言 - 蓝牙JDY-31-SPP串口通信实验
文章目录 蓝牙技术的发展历史SPP蓝牙串口BLE协议(超低功耗应用蓝牙协议) 常见通用蓝牙模块JDY-31-SPPHC05/06 Keil 工程开发模版main.c 源文件:接线方式:烧录工具:FlyMcu串口调试工具:XCOM蓝牙调试助手APP …...
算法39:Excel 表列序号
一、需求 给你一个字符串 columnTitle ,表示 Excel 表格中的列名称。返回 该列名称对应的列序号 。 例如: A -> 1 B -> 2 C -> 3 … Z -> 26 AA -> 27 AB -> 28 … 示例 1: 输入: columnTitle “A” 输出: 1 示例 2&…...

Android:ImageView xml方式配置selector 图片切换
1、在res/drawable目录下创建一个新的XML文件,比如selector_image.xml <?xml version"1.0" encoding"utf-8"?> <selector xmlns:android"http://schemas.android.com/apk/res/android"> <!-- 背景选择器 state_pre…...
Spring Boot 缓存 Cache 入门
Spring Boot 缓存 Cache 入门 1.概述 在系统访问量越来越大之后,往往最先出现瓶颈的往往是数据库。而为了减少数据库的压力,我们可以选择让产品砍掉消耗数据库性能的需求。 当然也可以引入缓存,在引入缓存之后,我们的读操作的代码ÿ…...
如何关闭谷歌浏览器自动更新
适用范围: 写自动化脚本时,需要安装浏览器驱动,安装浏览器驱动时需要下载对应的浏览器驱动版本,如果浏览器版本一直在自动更新的话,自动化脚本会报错浏览器版本和浏览器驱动不匹配,所以建议关闭谷歌浏览器自动更新&am…...
mybatis日志工厂
前言: 如果一个数据库操作,出现异常,我们需要排错,日志就是最好的助手 官方给我们提供了logImpl:指定 MyBatis 所用日志的具体实现,未指定时将自动查找。 默认工厂: 在配置文件里添加…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...
