数据结构——复杂度

总有一天你要一个人,再暗夜中,向那座桥走过去
文章目录
一、算法的复杂度
考察形式范例
二、算法的时间复杂度
大O的渐进表示法
常见的复杂度对比
例题:消失的数字
题目的三种思路
1.排序+遍历
2.减法
3.单身狗思想
三、空间复杂度
大O的渐进表示法
常见复杂度比较
四、复杂度判断总结
大家好,我是纪宁。
上篇文章已经为大家介绍了数据结构与算法,相信看过的人已经大值了解数据结构与算法了。在解决一个问题的时候,我们通常会使用各式各样的算法,那么,如何衡量一个算法的性能好坏或者效率高低呢?这里我们就要学习复杂度的概念。
本文在空间复杂度的求解处提到了函数栈帧这个概念,不懂的老铁可以去看博主肝了好久的老作品 从汇编代码探究函数栈帧的创建和销毁的底层原理
还有在时间复杂度和空间复杂度中都提到的冒泡排序算法
一、算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 ,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
考察形式范例
leetcode
腾讯面试题、剑指offer 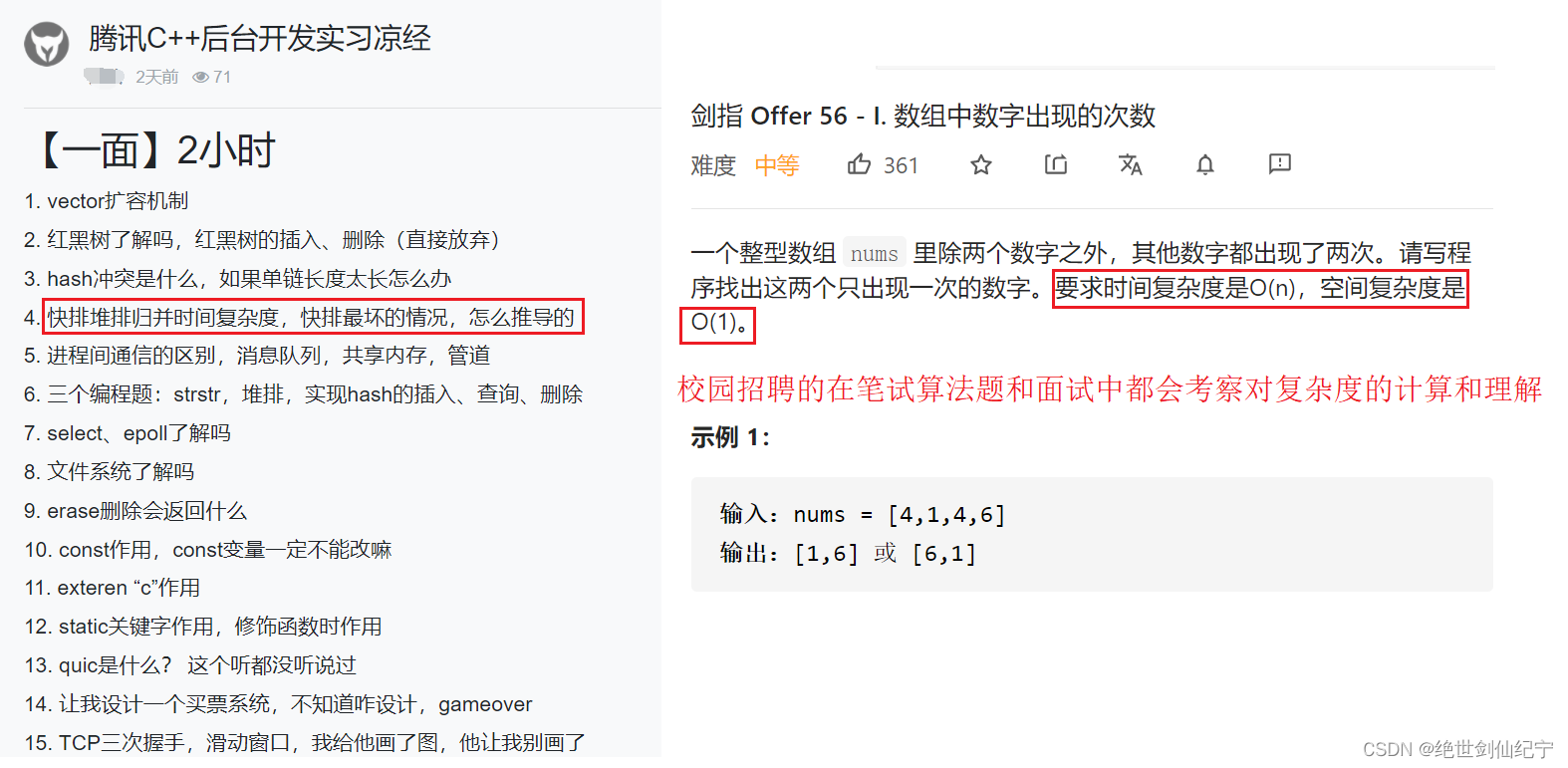
二、算法的时间复杂度
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。它可以算出一个理论时间值,这个值与与其中语句的执行次数成正比例。那么算法的时间复杂度,通俗来讲,就是算法中的基本操作的执行次数。
大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项(取极限后对记过影响最大的一项)
3、如果最高阶项存在且不是1,去除与这个最高阶项相乘的常数。得到的结果就是大O阶。
4、时间复杂度以最坏情况为准(如在数组中搜索数组,时间复杂度为O(N))
常见的复杂度对比
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}这段代码关键语句执行了 2N+10 次,只看最高项,为2N,再除去常数2,所以时间复杂度为O(N)
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}这段代码关键语句执行了 M+N 次,所以时间杂度为O(M+N)
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}这段代码关键语句执行了100次,为常数次,所以时间复杂度为O(1)
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}这段代码代码为冒泡排序算法,以最坏情况考虑(最后一次冒泡才排好序),第一次冒泡要比较 n-1次,第二次冒泡要比较 n-2 次......最后一次冒泡只需要比较 1 次,一共需要n趟比较。那么关键语句的执行次数为 (n-1)+(n-2)+(n-3)......+2+1=n*n/2(等差数列求和),所以冒泡排序的时间复杂度为 O(N^2)
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}这段代码为二分查找算法,以最快情况考虑(最后一个元素才找到或者没找到),二分查找时间复杂度计算比较难,我画图来解释一下。
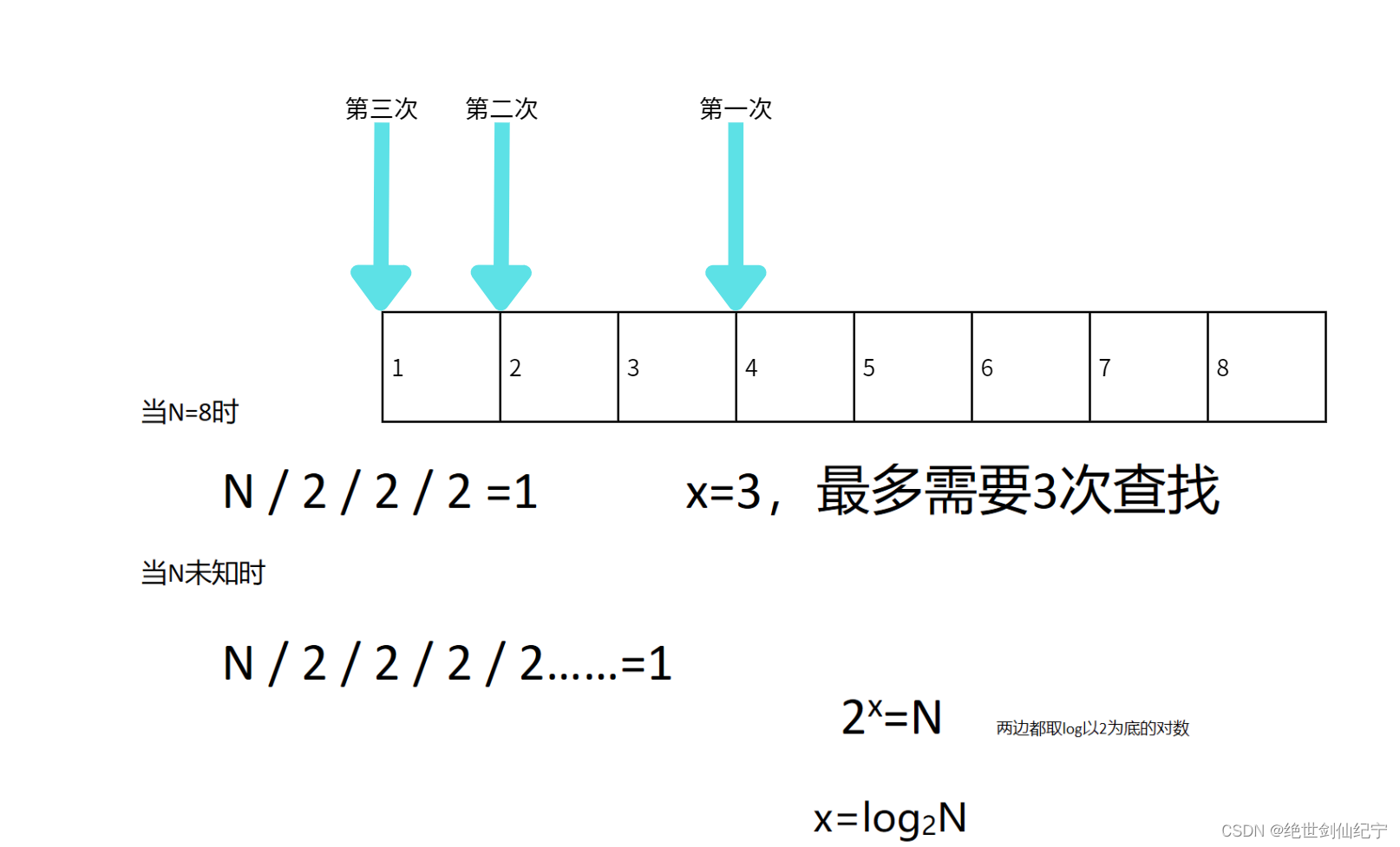
为了方便书写,我们通常将时间复杂度为 以2为底的对数简写为 O(logN)
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}这段代码是关于斐波那锲数列的递归解法,斐波那锲数列的递归法,用过的人都知道,只有理论意义,越递归,重复工作越多,越复杂,所以没有太大的实际意义。
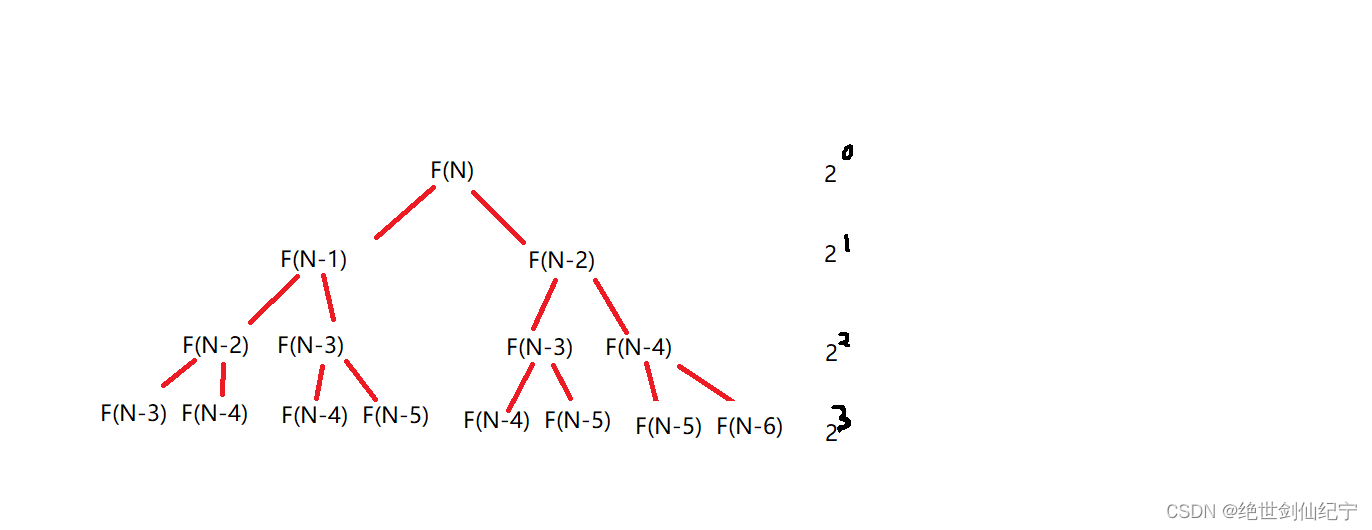
当N=0的时候,一共进行了2^N数量级次递归语句的执行,所以时间复杂度为log(2^N)
例题:消失的数字
题目
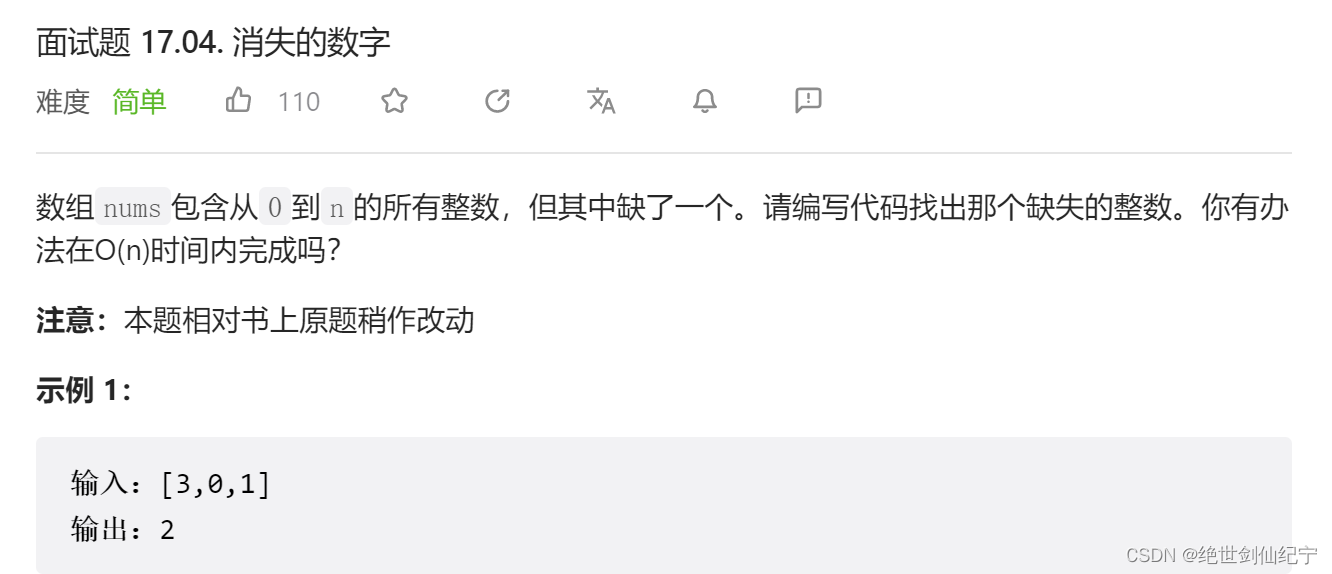
数组
nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?
示例 :
输入:[3,0,1]
输出:2
示例 2:
输入:[9,6,4,2,3,5,7,0,1]
输出:8
题目的三种思路
1.排序+遍历
先排序,如果发现有个数的下一个数减这个数不等于1,那么这个数的下一个数就是‘消失的数字’。排序如果采用冒泡排序的话,时间复杂度会不合适,所以采用快速排序算法。快速排序的时间复杂度是 O(logN*N),依然不符合时间复杂度要求大家可以自己去尝试优化一下排序算法。
2.减法
先用等差数列公式计算 1-n的值,再用这个值减去遍历数组的加和,得到的就是那个消失的数字。时间复杂度为O(N),符合要求。
int missingNumber(int* nums, int numsSize)
{int N = numsSize;int ret = N * (N + 1) / 2;//等差数列公式for (int i = 0; i < N; i++){ret -= nums[i];}return ret;
}3.单身狗思想
先用1-n 的所有值异或,再用结果异或数组中的所有值,相同的数字可以相互配对,异或的值等于0,所以就剩下一个‘消失的数字’对应的数,这个数就是消失的数字。
int missingNumber(int* nums, int numsSize)
{int N = numsSize;int x = 0;for (int i = 0; i <= N; i++){x ^= i;}for (int i = 0; i < N; i++){x ^= nums[i];}return x;
}三、空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度与定义变量的个数(额外开辟的空间数),计算规则也与时间复杂度相差无几。但函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间(函数栈帧申请的次数)来确定。
大O的渐进表示法
空间复杂度的大O渐进表示法通过计算额外开辟的空间数和函数栈帧的申请次数即可。
常见复杂度比较
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}因为冒泡排序中只创建了 exchange 这一个额外空间的变量,所以空间复杂度就是O(1)
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}这段代码开辟了(n+1)个额外空间,所以空间复杂度为O(N)
long long Fac(size_t N)
{if (N <3)return 1;return Fib(N - 1) * Fib(N-2);
}这段代码为斐波那契额数列的递归解法,这个解法时间复杂度达到了O(2^N),而空间复杂度却是O(N),因为它的函数栈帧其实只开辟了N次。为什么呢?真实情况是函数进入Fib(N-1)后,暂时是不会进入同行语句中的Fib(N-2)的,当Fib(N-1)递归结束后(一共开辟并释放了N次函数栈帧),程序才开始进入那一行的Fib(N-2)函数中,因为Fib(N-1)中已经开辟了很多空间,虽然已经还给了操作系统,但Fib(N-2)中所开辟的函数栈帧依然是在曾经Fib(N-1)的那块空间上,所以并没有再多余浪费空间开辟函数栈帧。
四、复杂度判断总结
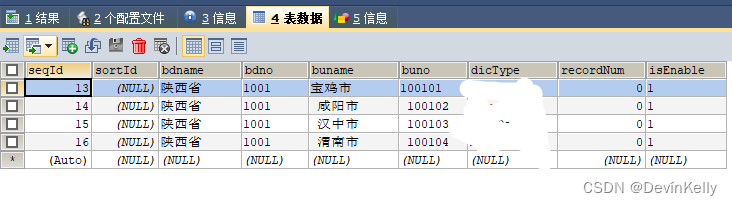
这个表格大家看一下应该可以轻易理解并记住的,主要是掌握时间和空间复杂度的计算。
| 52101314 | O(1) | 常数阶 |
| 3n+4 | O(N) | 线性阶 |
| 3n^2+4n+5 | O(N^2) | 平方阶 |
| 3log(2)n+4 | O(logN) | 对数阶 |
| 2n+2nlog(2)n+14 | O(NlogN) | NlogN阶 |
| n^3+2n^2+4n+6 | O(N^3) | 立方阶 |
| 2^n | O(2^N) | 指数阶 |
相关文章:

数据结构——复杂度
总有一天你要一个人,再暗夜中,向那座桥走过去 文章目录 一、算法的复杂度 考察形式范例 二、算法的时间复杂度 大O的渐进表示法 常见的复杂度对比 例题:消失的数字 题目的三种思路 1.排序遍历 2.减法 3.单身狗思想 三、空间复杂度…...

使用goldengate 迁移Oracle到postgresql
环境: --源端: IP:10.0.4.16 hostname:tencent Oracle数据库版本:12.2.0.1.0 ogg for oracle版本:19.1.0.0.4 SID:orcl --目标端: IP:10.0.4.16 hostname&#…...
ESP-C3入门20. CentOS开发环境及Jenkins流水线
一、准备环境 CentOS8已经正常安装Jenkins 二、升级 cmake cmake 升到 3.16以上。 cmake --version # 安装 g sudo yum install gcc-c export CXXg# 安装 CMake 的依赖项 sudo yum install -y openssl-devel# 下载 CMake 源码并进行编译安装 wget https://github.com/Kitwa…...

服务器被爬虫恶意攻击怎么办?
在有预算的情况可以采购第三方服务防火墙,没钱就使用开源的WAF进行防护。 # WAF防火墙的基本防护原理 WAF(Web 应用防火墙)可以使用多种技术来防止恶意爬虫攻击,例如: 1. 黑名单:WAF 可以使用黑名单技术来…...

JavaScript正则表达式之座机号/手机号验证校验规则
引用:https://www.bilibili.com/read/cv18300539/ 本文对利用正则表达式对手机号码进行了验证 支持格式: 座机 :xxx-xxxxxxxx、xxxxxxxxxxxx …座机区号的横杠可有可无 手机:xxxxxxxxxxx JavaScript: var: checkPhone (rule,…...
黑客学习手册(自学网络安全)
一、首先,什么是黑客? 黑客泛指IT技术主攻渗透窃取攻击技术的电脑高手,现阶段黑客所需要掌握的远远不止这些。 二、为什么要学习黑客技术? 其实,网络信息空间安全已经成为海陆空之外的第四大战场,除了国…...
、hook)【为了解决grad值是None的问题】)
获取非叶子节点的grad(retain_grad()、hook)【为了解决grad值是None的问题】
在调试过程中, 有时候我们需要对中间变量梯度进行监控, 以确保网络的有效性, 这个时候我们需要打印出非叶节点的梯度, 为了实现这个目的, 我们可以通过两种手段进行, 分别是: retain_grad()hook 不过我感觉“hook”比“retain_grad()”要麻烦.....,所以我感觉还是…...
JMeter(八):响应断言详解
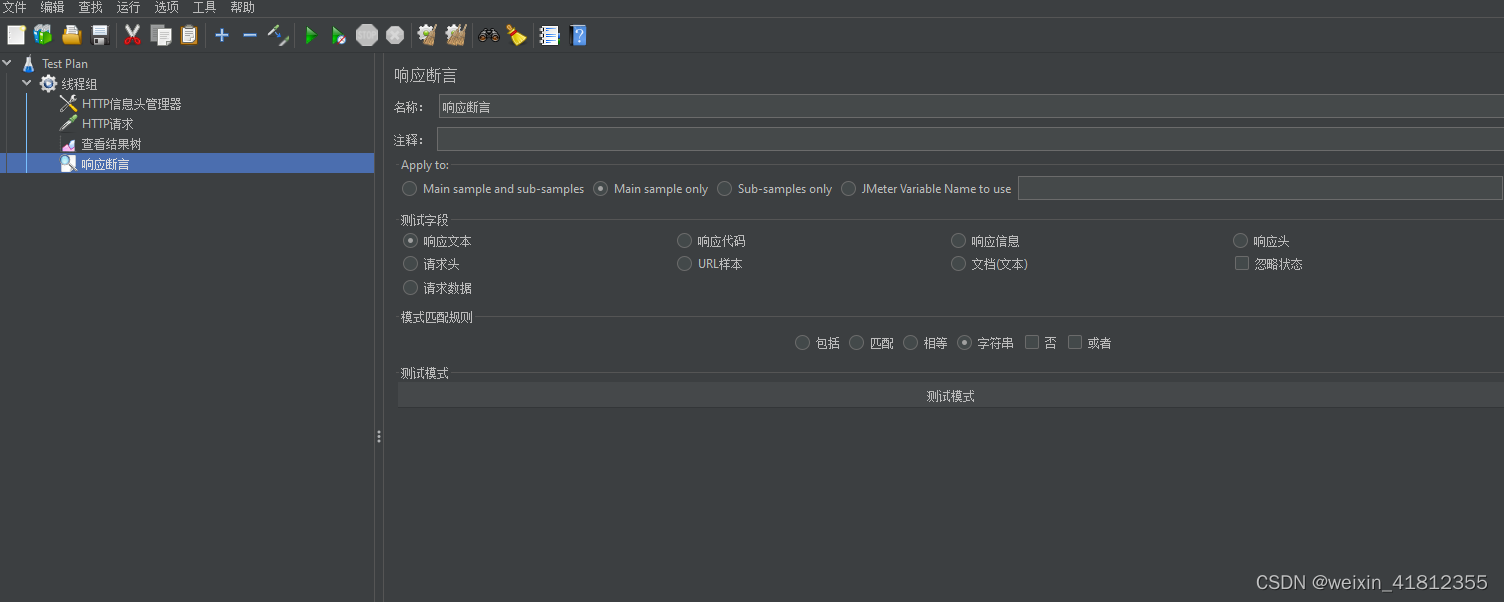
响应断言 :对服务器的响应进行断言校验 (1)应用范围: main sample and sub sample, main sample only , sub-sample only , jmeter variable 关于应用范围,我们大多数勾选“main sample only” 就足够了,因为我们一个请求,实质上只有一个请求。但是当我们发一个请求时,…...

【网络编程】IO复用的应用一:非阻塞connect
在connect连接中,若socket以非阻塞的方式进行连接,则系统内设置的TCP三次握手超时时间为0,所以它不会等待TCP三次握手完成,直接返回,错误为EINPROGRESS。 所以,我们可以通过判断connect时返回的错误码是…...

Spring注解开发,bean的作用范围及生命周期、Spring注解开发依赖注入
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaweb 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 Spring注解开发 一、注解开发定义Bean二、纯注解开发Bean三…...

C#设计模式之---原型模式
原型模式(Prototype Pattern) 原型模式(Prototype Pattern) 是用原型实例指定创建对象的种类,并且通过拷贝这些原型创建新的对象。原型模式是一种创建型设计模式。也就是用一个已经创建的实例作为原型,通过…...

STM32入门学习之外部中断
1.STM32的IO口可以作为外部中断输入口。本文通过按键按下作为外部中断的输入,点亮LED灯。在STM32的19个外部中断中,0-15为外部IO口的中断输入口。STM32的引脚分别对应着0-15的外部中断线。比如,外部中断线0对应着GPIOA.0-GPIOG.0,…...
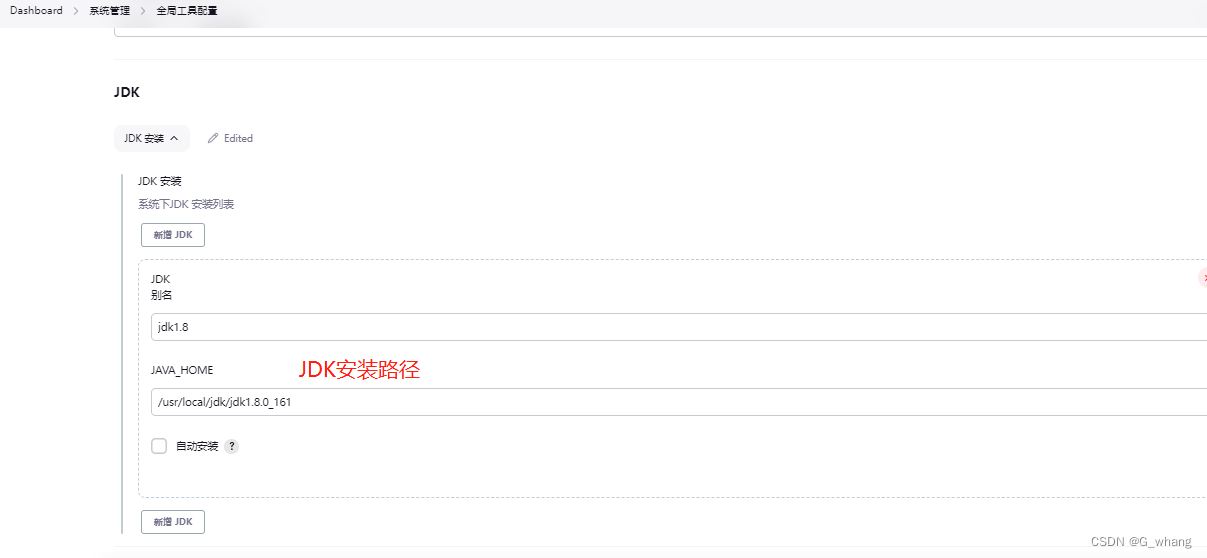
Jenkins 配置maven和jdk
前提:服务器已经安装maven和jdk 一、在Jenkins中添加全局变量 系统管理–>系统配置–>全局属性–>环境变量 添加三个全局变量 JAVA_HOME、MAVEN_HOME、PATH 二、配置maven 系统管理–>全局工具配置–>maven–>新增 新增配置 三、配置JDK 在系统管…...
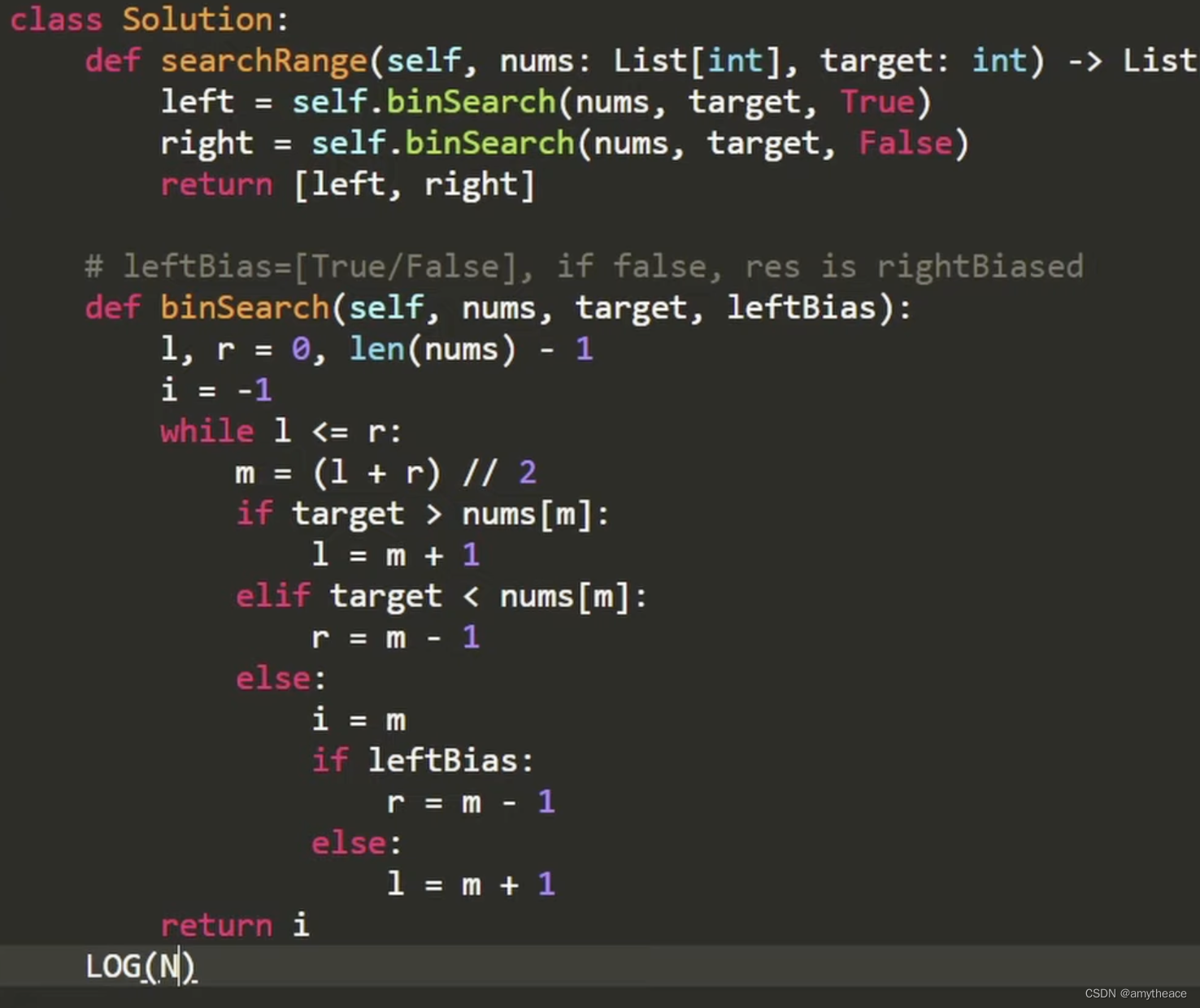
Leetcode | Binary search | 22. 74. 162. 33. 34. 153.
22. Generate Parentheses 要意识到只要还有左括号,就可以放到path里。只要右括号数量小于左括号,也可以放进去。就是valid的组合。recurse两次 74. Search a 2D Matrix 看成sorted list就好。直接用m*n表示最后一位的index,并且每次只需要 …...

生命在于折腾——面试问题汇总
这里面的问题都是我参加面试时候遇到的问题,大家就这样看吧。 一、个人情况 1、自我介绍 2、为什么离开上一家公司 3、有没有参加过HVV 4、介绍一下上家公司的项目 5、小程序和公众号渗透测试做过么 6、实习工资多少 7、有挖过漏洞么 二、基础知识 1、信息收集的…...
<Java>Map<String,Object>中解析Object类型数据为数组格式
背景: 前端:入参为字符串和数组类型;通过json字符串传给后台, 后台:后台通过工具解析为Map<String,Object>,然后需要解析出Map里面的数组值做操作; 需求: 入参&…...

别再分库分表了,试试TiDB!
什么是NewSQL 传统SQL的问题 升级服务器硬件 数据分片 NoSQL 的问题 优点 缺点 NewSQL 特性 NewSQL 的主要特性 三种SQL的对比 TiDB怎么来的 TiDB社区版和企业版 TIDB核心特性 水平弹性扩展 分布式事务支持 金融级高可用 实时 HTAP 云原生的分布式数据库 高度兼…...

Java进阶之Dump文件初体验
视频地址:https://www.bilibili.com/video/BV1Ak4y137oh 学习文章:https://d9bp4nr5ye.feishu.cn/wiki/VQoAwlzrXiLFZekuLIyc1uK5nqc 最近线上频繁的内存告警,同事A通过分析dump文件解决了这个问题,我当然是不会放过这种学习的机…...

基于扩展(EKF)和无迹卡尔曼滤波(UKF)的电力系统动态状态估计(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
曲线拟合(MATLAB拟合工具箱)位置前馈量计算(压力闭环控制应用)
利用PLC进行压力闭环控制的项目背景介绍请查看下面文章链接,这里不再赘述。 信捷PLC压力闭环控制应用(C语言完整PD、PID源代码)_RXXW_Dor的博客-CSDN博客闭环控制的系列文章,可以查看PID专栏的的系列文章,链接如下:张力控制之速度闭环(速度前馈量计算)_RXXW_Dor的博客-CSD…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
