数学分析:流形的线性代数回顾

因为是线性的,所以可以把所有的系数都提取出去。这也是多重线性代数的性质。可以看成基本的各项自变量的乘法。

这里可以看到两个不同基向量下,他们的坐标转化关系。
 引出了张量积,也就是前面提到的内容。
引出了张量积,也就是前面提到的内容。

对偶空间的例子总是比较美好。
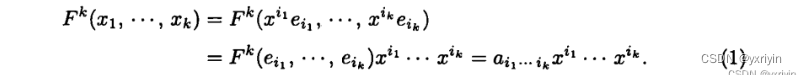
因为e^i就是把x的第i个坐标给取出来。所以就得到了(10),每一个张量基的组成部分都是取到对应的坐标。他们作用在x上就会得到(1)

这个意思是说,对于任何k形式,我们都可以通过一种运算得到斜对称形式。

这里我们看到了为什么要引入行列式,是因为一个取坐标的操作的张量积放到斜对称形式的推导里面,会得到一个式子,这个式子就是行列式的公式。然后也说了为什么要引入外积,因为斜对称形式的张量积一般就不是斜对称了,引入外积的话就是为了保证还是斜对称。公式15就是外积的定义。其实这里可以感受到,斜对称应该是一个非常重要的形式,我们后面看。

这个式子还是要仔细理解的。前面就是k形式,后面是k形式的求和。

求和的系数取决于交换次数。

按照前面的公式,我们可以发现取坐标的外积,最终就是这些坐标分别取出来组成一个矩阵的行列式的值。
 这里我们看到,是想把普通k形式都转成斜对称形式,引入了一个运算A,本来k形式就是F=ae1xe2...exn
这里我们看到,是想把普通k形式都转成斜对称形式,引入了一个运算A,本来k形式就是F=ae1xe2...exn
引入A之后,变成了斜对称形式,就有了行列式。要考虑斜对称之间的运算还是斜对称,就引入了外积。

最后这一段看不太懂,需要再理解下。问了GPT,它的意思是对于n维线性空间,如果你的k形式的k>n。例如k=3,n=2, 那么按照反对称的定义,里面比如有两个元素是一样的。例如取坐标,二维空间就两个坐标可以取,但你要取3次,必有两次是重复的。重复的就代表斜对称必须为0.

看着比较费解,冲对偶映射去理解,X->Y,会变成Y*->X*,于是l*F^k肯定是相当于Fx.最终就是(25),27,28,29公式形式还是很优美的。

这里提到了坐标,我们得先复习:
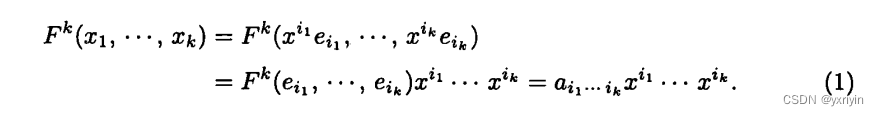
k形势下的坐标形式,后面的y的一堆的乘积就是坐标,前面是k形式作用在基上的值。
所以我们得到了两个不同空间中的k形式的一些关系。Y上的k形式,作用在Y的基上引出的系数b。和对偶映射X上的k形式,作用在X的基上引出的系数a,他们之间的系数关系和基的关系的表达式。

这个结论是说明:我们通过对偶映射把Y上的取坐标转到x上的一个映射,它等价于一堆取坐标函数的和。
这个更一般的结论和5应该是一样的。我们得到了两组基向量的关系,他们对应的对偶映射的k形式也是具有类似关系的。
在整理下:我们对于普通的k形式,想要引入斜对称,就引入了运算A,我们发现运算A本质上是可以看成一个行列式。而斜对称之间的运算需要在符合斜对称,于是引入了外积。同时我们发现,行列式可以看成取坐标运算符的外积的操作。于是我们就会开始研究取坐标操作运算之间的外积。然后得到了一系列的坐标转化公式。
相关文章:

数学分析:流形的线性代数回顾
因为是线性的,所以可以把所有的系数都提取出去。这也是多重线性代数的性质。可以看成基本的各项自变量的乘法。 这里可以看到两个不同基向量下,他们的坐标转化关系。 引出了张量积,也就是前面提到的内容。 对偶空间的例子总是比较美好。 因为…...

前端请求后端接口返回错误码
1、如果 HTTP Code 是 2xx 范围内的,那通常表明请求已经成功处理,并且可以根据具体的 HTTP Code 进一步判断请求的处理结果。比如: HTTP Code 200 表明请求成功,并返回了请求资源;HTTP Code 204 表明请求成功…...

【Java Web】Nacos 介绍和安装教程
文章目录 1. Nacos 介绍1.1 Nacos 的定义1.2 Nacos 的主要功能1.2.1 服务注册与发现1.2.2 配置管理1.2.3 动态 DNS 服务1.2.4 服务和元数据管理 1.3 Nacos 的适用场景1.3.1 微服务架构1.3.2 动态配置管理1.3.3 多环境部署1.3.4 云原生应用 2. Nacos 的核心组件2.1 服务注册与发…...

web漏洞-java安全(41)
这个重点是讲关于java的代码审计,看这些漏洞是怎么在java代码里面产生的。 #Javaweb 代码分析-目录遍历安全问题 这个漏洞原因前面文章有,这次我们看看这个漏洞如何在代码中产生的,打开靶场 解题思路就是通过文件上传,上传文件…...
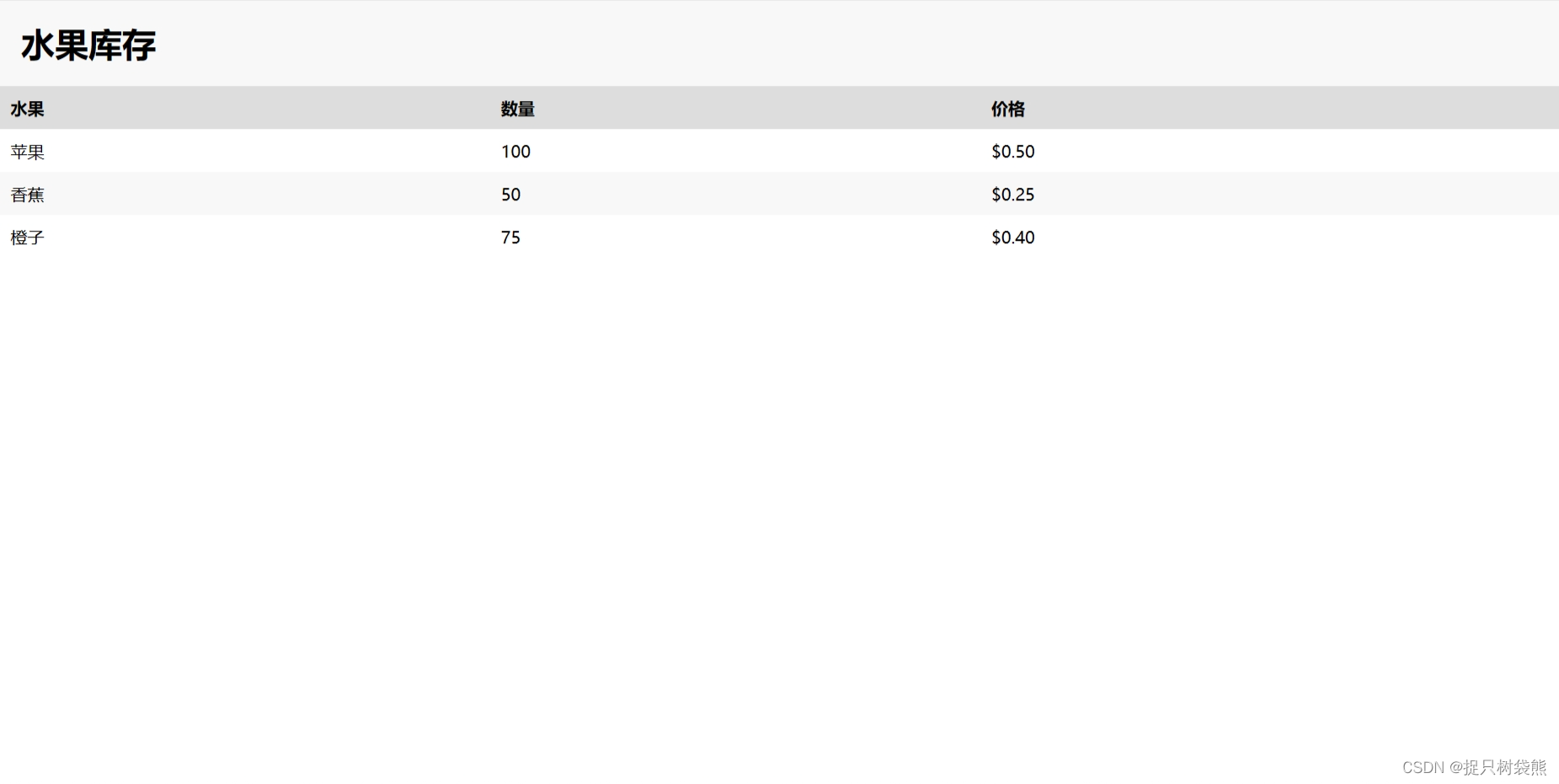
用CSS和HTML写一个水果库存静态页面
HTML代码: <!DOCTYPE html> <html> <head><link rel"stylesheet" type"text/css" href"styles.css"> </head> <body><header><h1>水果库存</h1></header><table>…...

【回眸】备考PMP考点汇总 三(距离考试还有20天)
目录 前言 【回眸】备考PMP考点汇总 三(距离考试还有20天) 29、管理质量 30、获取资源 31、建设团队 32、管理团队 33、管理沟通 34、实施风险应对 35、实施采购 36、管理相关方参与 37、监控项目工作(10%) 38、实施整…...

新房的收房验房注意事项
文章目录 流程注意事项准备检查材料手续整体结构验收水电检测门窗结构地面工程墙面工程顶面工程阳台厨房卫生间户外设施 流程注意事项 只要发现问题,不管大小,都要在相关文件或表格中记录下来,而不管开发商以及陪同的收房人员如何花言巧语。…...
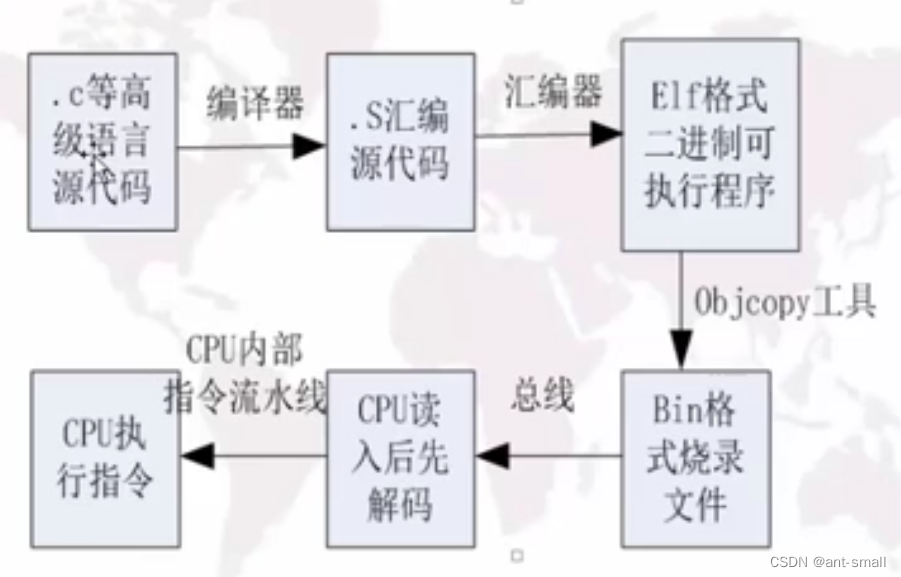
ARM裸机-5
1、可编程器件的编程原理 1.1、电子器件的发展方向 模拟器件-->数字器件 ASIC-->可编程器件 1.2、可编程器件的特点 CPU在固定频率的时钟控制下节奏运行。 CPU可以通过总线读取外部存储设备中的二进制指令集,然后解码执行。 这些可以被CPU解码执行的二进制指…...
——分布式搜索ElasticSeach场景使用)
SpringCloud学习路线(11)——分布式搜索ElasticSeach场景使用
一、DSL查询文档 (一)DSL查询分类 ES提供了基于JSON的DSL来定义查询。 1、常见查询类型: 查询所有: 查询出所有的数据,例如,match_all全文检索(full text)查询: 利用…...

负数补码表示
负数补码作用 在计算机中加法和减法采用同一电路,即用加法表示减法,如7 - 2 5变成7 ( -2) 5,这样减法的电路不用另行设计,但计算机中数据以二进制存储,没有负号,因此设计负数补码代…...
ChatGPT结合知识图谱构建医疗问答应用 (一) - 构建知识图谱
一、ChatGPT结合知识图谱 在本专栏的前面文章中构建 ChatGPT 本地知识库问答应用,都是基于词向量检索 Embedding 嵌入的方式实现的,在传统的问答领域中,一般知识源采用知识图谱来进行构建,但基于知识图谱的问答对于自然语言的处理…...
C++ 类和对象
面向过程/面向对象 C语言是面向过程,关注过程,分析出求解问题的步骤,通过函数调用逐步解决问题 C是基于面对对象的,关注的是对象——将一件事拆分成不同的对象,依靠对象之间的交互完成 引入 C语言中结构体只能定义…...

c# 此程序集中已使用了资源标识符
严重性 代码 说明 项目 文件 行 禁止显示状态 错误 CS1508 此程序集中已使用了资源标识符“BMap.NET.WindowsForm.BMapControl.resources” BMap.NET.WindowsForm D:\MySource\Decompile\BMap.NET.WindowsForm\CSC 1 活动 运行程序时&a…...

WPF实战学习笔记30-登录、注册服务添加
登录、注册服务添加 添加注册数据类型添加注册UI修改bug UserDto的UserName更改为可null类型Resgiter 添加加密方法修改控制器 添加注册数据类型 添加文件MyToDo.Share.Models.ResgiterUserDto.cs using System; using System.Collections.Generic; using System.Linq; us…...

GDAL C++ API 学习之路 OGRGeometry 圆弧类 OGRCircularString
OGRCircularString Class <ogrsf_frmts.h> OGRCircularString 类是 OGR 几何库中的一个类,用于表示圆弧字符串(circular string)类型的几何图形。圆弧字符串是由一系列圆弧段组成的几何图形,每个圆弧段由三个点定义…...
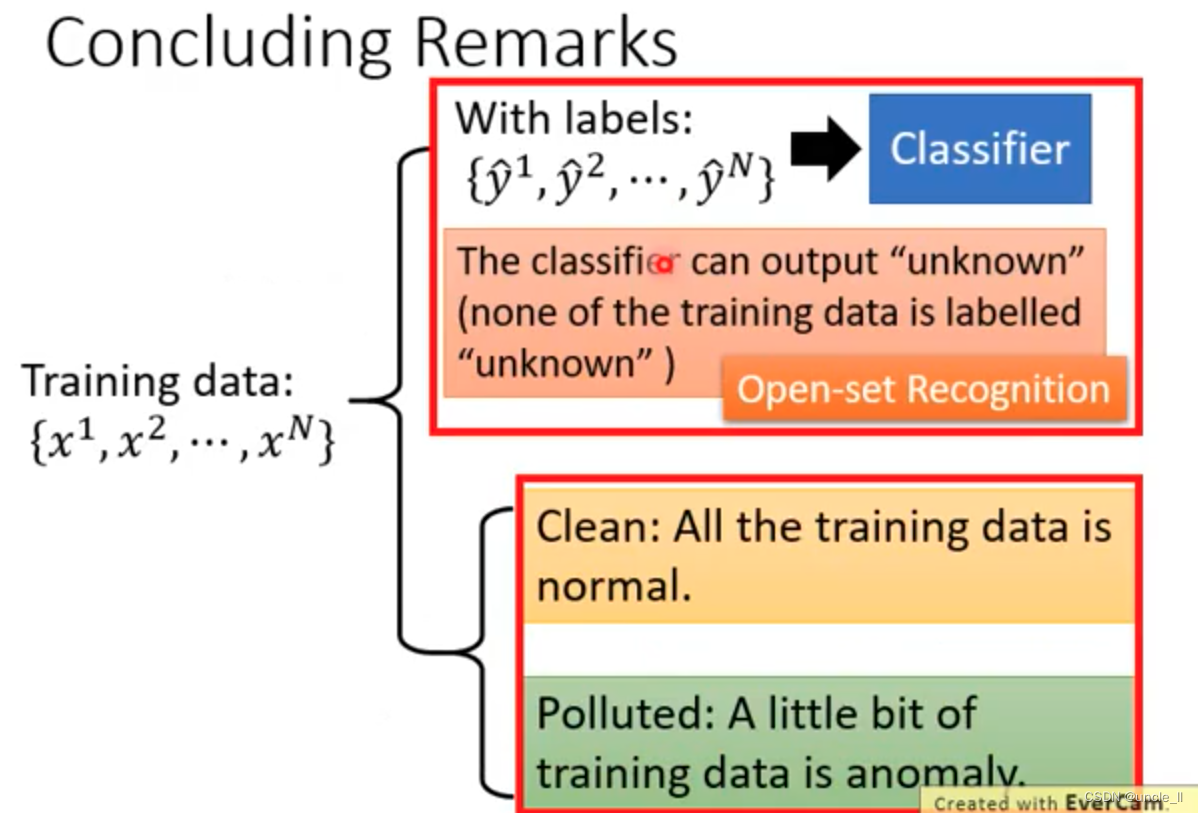
机器学习:异常检测
问题定义 anomaly,outlier, novelty, exceptions 不同的方法使用不同的名词定义这类问题。 应用 二分类 假如只有正常的数据,而异常的数据的范围非常广的话(无法穷举),二分类这些不好做。另外就…...

flask中的蓝图
flask中的蓝图 在 Flask 中,蓝图(Blueprint)是一种组织路由和服务的方法,它允许你在应用中更灵活地组织代码。蓝图可以大致理解为应用或者应用中的一部分,可以在蓝图中定义路由、错误处理程序以及静态文件等。然后可以…...

Spring Cloud+Spring Boot+Mybatis+uniapp+前后端分离实现知识付费平台免费搭建
Java版知识付费-轻松拥有知识付费平台 多种直播形式,全面满足直播场景需求 公开课、小班课、独立直播间等类型,满足讲师个性化直播场景需求;低延迟、双向视频,亲密互动,无论是互动、答疑,还是打赏、带货、…...
)
uniapp 瀑布流 (APP+H5+微信小程序)
WaterfallsFlow.vue <template><view class"wf-page" :class"props?.paddingC ? paddingC : "><!-- left --><view><view id"left" ref"left" v-if"leftList.length"><viewv-for…...
医疗小程序:提升服务质量与效率的智能平台
在医疗行业,公司小程序成为提高服务质量、优化管理流程的重要工具。通过医疗小程序,可以方便医疗机构进行信息传播、企业展示等作用,医疗机构也可以医疗小程序提供更便捷的预约服务,优化患者体验。 医疗小程序的好处 提升服务质量…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
