完全背包
动态规划解题步骤 :
动态规划问题一般从三个步骤进行考虑。
步骤一:集合和集合的状态
所谓的集合,就是一些方案的集合。
用 g[i][j] 表示从前 i 种物品中进行选择,且总体积不大于 j 的各个选法获得的价值的集合。注意:g[i][j] 不是一个数,是一堆数。
例如 g[2][3] 从前 2 种物品中进行选择,且总体积不大于 3 的各个选法获得的价值的集合。
g[2][3] 的可选择方案包括:
方案一:都不选,总价值为 0。
方案二:选 1 件 物品 1,总价值为 2。
方案三:选 2 件物品 1,总价值为 4。
方案四:选 3件 物品 1,总价值为 6。
方案五:选 1 件物品 2,总价值为 4。
方案六:选 1 件物品 2,一件物品 1,总价值为 6。
所以 g[2][3] = {0,2,4,6,4,2}。
i j 取不同的值,对应不同的 g[i][j],也就是对应不同的集合。
用 f[i][j] 表示从前 i 种物品中进行选择,总体积小于等于 j 所能获得的最大价值。很明显,f[i][j] 就是 g[i][j] 中的最大值。i j 取不同的值,就对应不同的 f[i][j]。我们把 f[i][j] 叫做集合的状态。
例如 f[2][3] 表示从前 2 种物品中进行选择,且总体积不大于 3 的获得的最大价值。f[2][3] = max(g[2][3] ) = max( 0,2,4,6,4,2) = 6。
g[i][j] 的最大值就是 f[i][j]。
如果我们能把所有集合对应的最大值都求出来,即求出了 f[0][0] ~ f[N][V], f[N][V] 的含义是在前 N 种物品中进行选择,总体积不大于 V 所获得的最大价值,就是我们要找的答案。
注意,我们不需要把各个集合的所有元素都找出来,只需要求出各个集合的最大值,就能找到答案。下面就是如何求出各个集合的最大值。
步骤二:状态计算
g[i][j] 是从前 i 种物品中进行选择,且总体积不大于 j 的各个选法获得的价值的集合。
f[i][j] 是从前 i 种物品中进行选择,总体积小于等于 j 所能获得的最大价值。
f[i][j] 是集合 g[i][j] 的最大值。
所谓的状态计算是指,如何将把 f[i][j] 算出来。
如果把各个集合 g[i][j] 的状态 f[i][j] 求出来, f[N][V] 就是要找的答案。
回想一下 0 1 背包问题。
01 背包问题把 g[i][j]划分成了 A B 两部分,分别求出这两个部分对应的最大值,然后两者取最大值就是整体 g[i][j] 的最大值,就是 f[i][j]。
01 背包根据是否选择第 i 件物品,也就是第 i 件物品选 0 个还是 1 个,把 g[i][j] 划分成了 A B 两部分,分别求出这两个部分的最大值,然后两者取最大值就是整体 g[i][j] 的最大值,也就求出了 f[i][j]。
完全背包问题也是根据第 i 件物品的选择数量,把 g[i][j] 划分成不同的部分,分别求出各个部分的最大值,取各个部分最大值中的最大值,就是整体 g[i][j] 的最大值,也就求出了 f[i][j]。
因为每种物品的数量是无限的,根据第 i 种物品的选择数量可以把 g[i][j] 分为这样几部分:
A 部分: 第 i 种物品选 0 件。
B 部分:第 i 件物品选 1 件。
C 部分: 第 i 件物品选 2 件。
X 部分: 第 i 件物品选 x 件。
. . . . .
因为选择物品的总体积不能 j,所以第 i 件物品最多选多选j / vivi 向下取整件。
对于 A 部分:第 i 件物品选 0 件。等价于从前 i - 1 种物品中选择商品,且总体积不超过 j 的各个价值的集合,也就是 g[i - 1][j]。g[i - 1][j] 这个集合中的最大值是 f[i - 1][j] ,所以 A 部分的最大值就是 f[i - 1][j]。
对于 B 部分:第 i 件物品选 1 件, 1 个 i 物品会占据 vivi 的背包空间,剩下的背包空间为 j - vivi 。可以从前 i - 1 种物品中,选出总体积小于等于j - vivi 的物品放入背包。
从前 i - 1 种物品中,选出总体积小于等于j - vivi 的各个方案获得的价值集合为 g[i - 1][j - vivi ],所以 B 部分的元素为 g[i - 1][j - vivi ] 中各个元素加上 wiwi 。g[i - 1][j - vivi ] 中的最大值为 f[i - 1][j - vivi ],所以 B 部分的最大值为 f[i - 1][j - vivi ] + wiwi。
对于 X 部分:第 i 件物品选 x 件, x 个 i 物品会占据 x * vivi 的背包空间,剩下的背包空间为 j - x * vivi 。可以从前 i - 1 种物品中,选出总体积小于等于j - x * vivi 的物品放入背包。
从前 i - 1 种物品中,选出总体积小于等于j - x * vivi 的各个方案获得的价值集合为 g[i - 1][j - x * vivi ],所以 x 部分的元素为 g[i - 1][j - x * vivi ] 中各个元素加上 x * wiwi 。g[i - 1][j - x * vivi ] 中的最大值为 f[i - 1][j - x * vivi ],所以 B 部分的最大值为 f[i - 1][j - x * vivi ] + x * wiwi。
例如 g[2][4]。
第二种物品的体积为 2,选择物品的总体积不能超过 4。所以第二件物品可以选择:0件、1件、2件。
因此 g[2][4] 可以分成以下几部分:
A 部分:第二件物品选 0 件。A 部分的最大值为: f[i - 1][j - 0 * vivi] + 0 * wiwi 。 B 部分:第二件物品选 1 件。B部分的最大值为: f[i - 1][j - 1 * vivi ] + 1 * wiwi 。 C 部分:第二件物品选 2 件。C 部分的最大值为:f[i - 1][j - 2 * vivi ] + 2 * wiwi 。 g[2][4] 中的最大值为 max(A,B,C)。
通过上面分析,我们可以知道,g[i][j] 可以分成若干部分:
A 部分是第 i 种物品选 0 个对应所有选法获的价值的集合,最大值是 f[i - 1][j]。 B 部分是第 i 种物品选 1 个对应所有选法获的价值的集合,最大值是 f[i-1][j - vivi] + wiwi。 X 部分是第 i 种物品选 x 个对应所有选法获的价值的集合,最大值是 f[i - 1][j - x * wiwi]。 所以 g[i][j] 的最大值就是所有子集的最大值中最大的那个,也就是 f[i][j] = max(A, B ,····) 即:
展开式为:f[i] [j] = max( f[i-1][j] , f[i - 1][j - vivi]+w , f[i - 1][j - 2 * vivi] + 2 * w , f[i - 1][j - k * vivi ] + k * w , .....) 其中 k <= j / w。
从计算公式可以看出:
f[i][j] 是由 f[i - 1][j - k * vivi ] (0 <= k <= j / wiwi) 和 wiwi 计算出来的。 f[i][j]的值是可以从前面已经计算出的 f 值求出来。 如果我们能确定 f[i][j] 的一部分初始值,就能通过该公式,一步步计算得出 f[N][V],也就是我们要找的答案。 步骤三:确定初始值
完全背包问题的有些状态是能够直接确定的。
例如 f[0][0]。
f[0][0] 的含义是:
从前 0 种物品中选择,并且选出的物品总体积小于等于0 时所能得到的最大价值。 总体积小于等于 0,说明一种物品都不能选择。 因此 f[0][0] = 0。同理 f[1][0] = 0,f[2][0] = 0 ··· f[N][0] = 0。 有了这些初始值,通过 i 从 1 遍历 N,j 从 1 遍历 V,第 i 种物品的选择数量 k 从 0 遍历到 j / wiwi 就能一步步求出所有的 f[i][j] 了。
例如求 f[1][1]:
f[1][1] = max{f[0][1],f[0][0] + 2} = max(0,2) = 2。 求 f[1][2]:
f[1][2] = max{f[0][2],f[0][1] + 2,f[0][0] + 4} = max(0,2,4) = 4。 最后 f[N][V] 就是要找的答案。
这时候就可以写代码了:
#include<iostream>
using namespace std;const int N = 1010;int n, m;
int f[N][N], v[N], w[N];int main(){cin >> n >> m;for(int i = 1; i <= n; i ++ )cin >> v[i] >> w[i];for(int i = 0; i <= m; i++)//初始化{f[0][i] = 0;}for(int i = 1; i <= n; i ++ )for(int j = 0; j <= m; j ++ )for(int k = 0; k * v[i] <= j; k ++ )f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);//求出每一个 f[i][j]cout << f[n][m] << endl;
}
...
优化 :
动态规划的优化一般都是对代码或者状态计算方程进行一个等价变形。 在考虑动态规划问题的时候,一定要先把基本的形式写出来,然后再对它进行优化。
看一下 f[i][j] 和 f[i][j - vivi] 的求解公式:
f[i][j] = max( f[i-1][j] , f[i-1][j - vivi] + w , f[i-1][j - 2 * vivi] + 2 * w , f[i-1][j - 3 * vivi] + 3 * w , .....)。
f[i][j - vivi] = max( f[i-1][j - vivi] , f[i-1][j - 2 * vivi] + w , f[i-1][j - 3 * vivi] + 2 * w , .....) 。
由上两式,可得出如下递推关系:
f[i][j] = max(f[i][j-v] + w , f[i-1][j])
有了上面的关系,那么其实 k 循环可以不要了,核心代码优化成这样:
for(int i = 1; i <= n; i ++ ){for(int j = 0; j <= m; j ++ ){if(v[i] <= j)//第 i 种能放进去f[i][j] =max(f[i - 1][j], f[i][j - v[i]] + w[i]);else//如果第 i 件物品不能放进去f[i][j] = f[i - 1][j];}}
完整代码:
#include<iostream>
using namespace std;const int N = 1010;int n, m;
int f[N][N], v[N], w[N];int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++ )cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++ ){for(int j = 0; j <= m; j ++ ){if(v[i] <= j)f[i][j] =max(f[i - 1][j], f[i][j - v[i]] + w[i]);elsef[i][j] = f[i - 1][j];}}cout << f[n][m] << endl;
}
接着对比下完全背包的核心代码与 01背包的核心代码:
f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);//01背包f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);//完全背包问题
//01背包代码优化这里有详细说明
因为和01背包代码很相像,我们很容易想到进一步优化。核心代码可以改成下面这样:
for(int i=1;i<=n;i++){for(int j=v[i];j<=m;j++)//注意了,这里的j是从小到大枚举,和01背包不一样{f[j] = max(f[j],f[j-v[i]]+w[i]);}
}
综上所述,完全背包的最终写法如下:
#include<iostream>
using namespace std;
const int N=1010;
int f[N];
int v[N],w[N];
int main(){int n,m;cin>>n>>m;for(int i = 1 ; i <= n ;i ++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=v[i];j<=m;j++){f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m]<<endl;
}相关文章:

完全背包
动态规划解题步骤 : 动态规划问题一般从三个步骤进行考虑。 步骤一:集合和集合的状态 所谓的集合,就是一些方案的集合。 用 g[i][j] 表示从前 i 种物品中进行选择,且总体积不大于 j 的各个选法获得的价值的集合。注意:g[i][j] 不是一个数…...
【软件测试】webdriver常用API演示(Java+IDEA+chrome浏览器)
1.元素定位方法 对象的定位应该是自动化测试的核心,要想操作一个对象,首先应该识别这个对象。一个对象就是一个人一样,他会有各种的特征(属性),如比我们可以通过一个人的身份证号,姓名…...

Linux安装MySQL 8.1.0
MySQL是一个流行的开源关系型数据库管理系统,本教程将向您展示如何在Linux系统上安装MySQL 8.1.0版本。请按照以下步骤进行操作: 1. 下载MySQL安装包 首先,从MySQL官方网站或镜像站点下载MySQL 8.1.0的压缩包mysql-8.1.0-linux-glibc2.28-x…...

多线程面试相关的一些问题
面试题 1. 常见的锁策略相关的面试题 2. CAS相关的面试题 3. Synchronized 原理相关的面试题 4. Callable 接口相关的面试题 1. 常见的锁策略 乐观锁 vs 悲观锁 悲观锁: 总是假设最坏的情况,每次去拿数据的时候都认为别人会修改,所以每次在拿数据的时候都…...
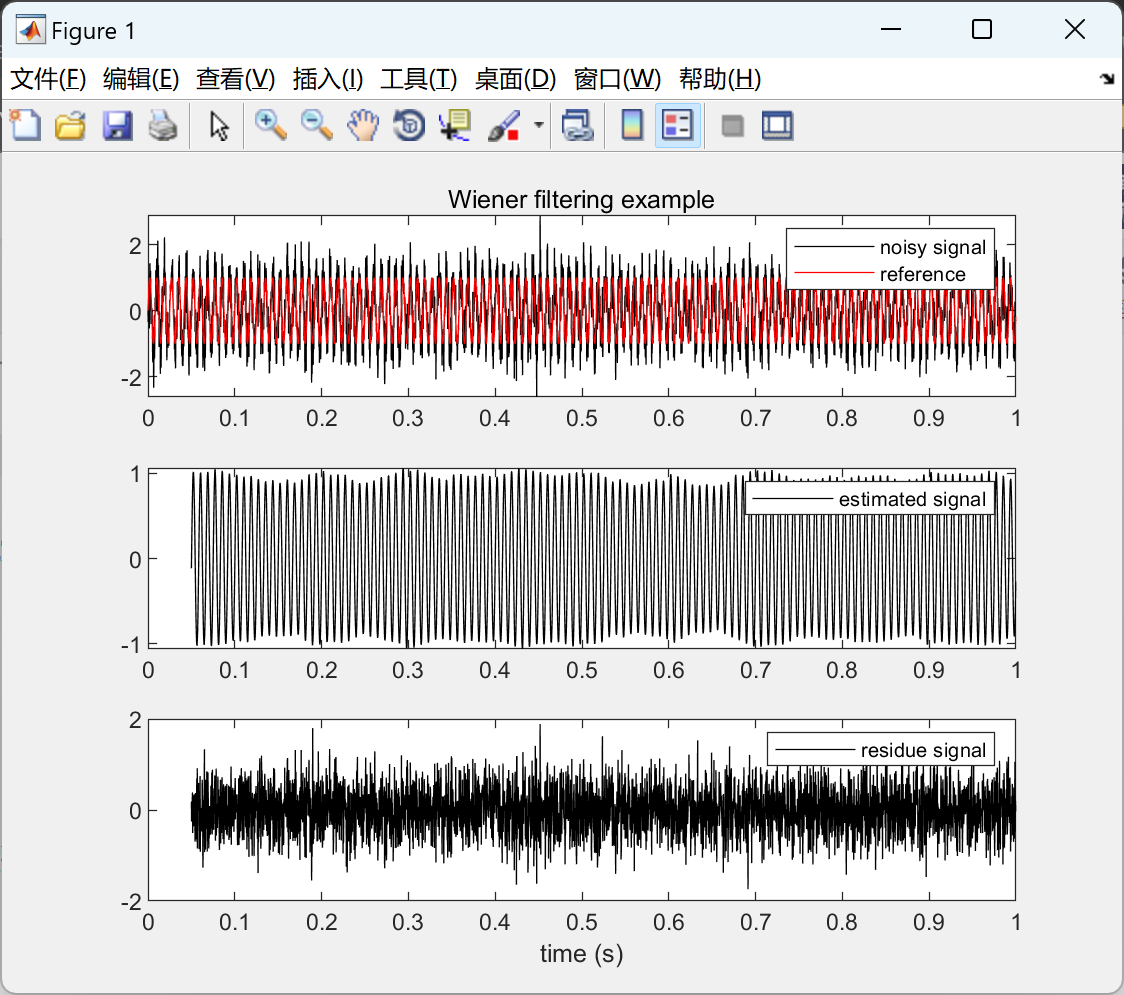
【使用维纳滤波进行信号分离】基于维纳-霍普夫方程的信号分离或去噪维纳滤波器估计(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Vue+axios如何解决跨域
1、为什么会产生跨域? 出于浏览器的同源策略限制。 同源策略(Sameoriginpolicy)是一种约定,是浏览器的一种安全机…...
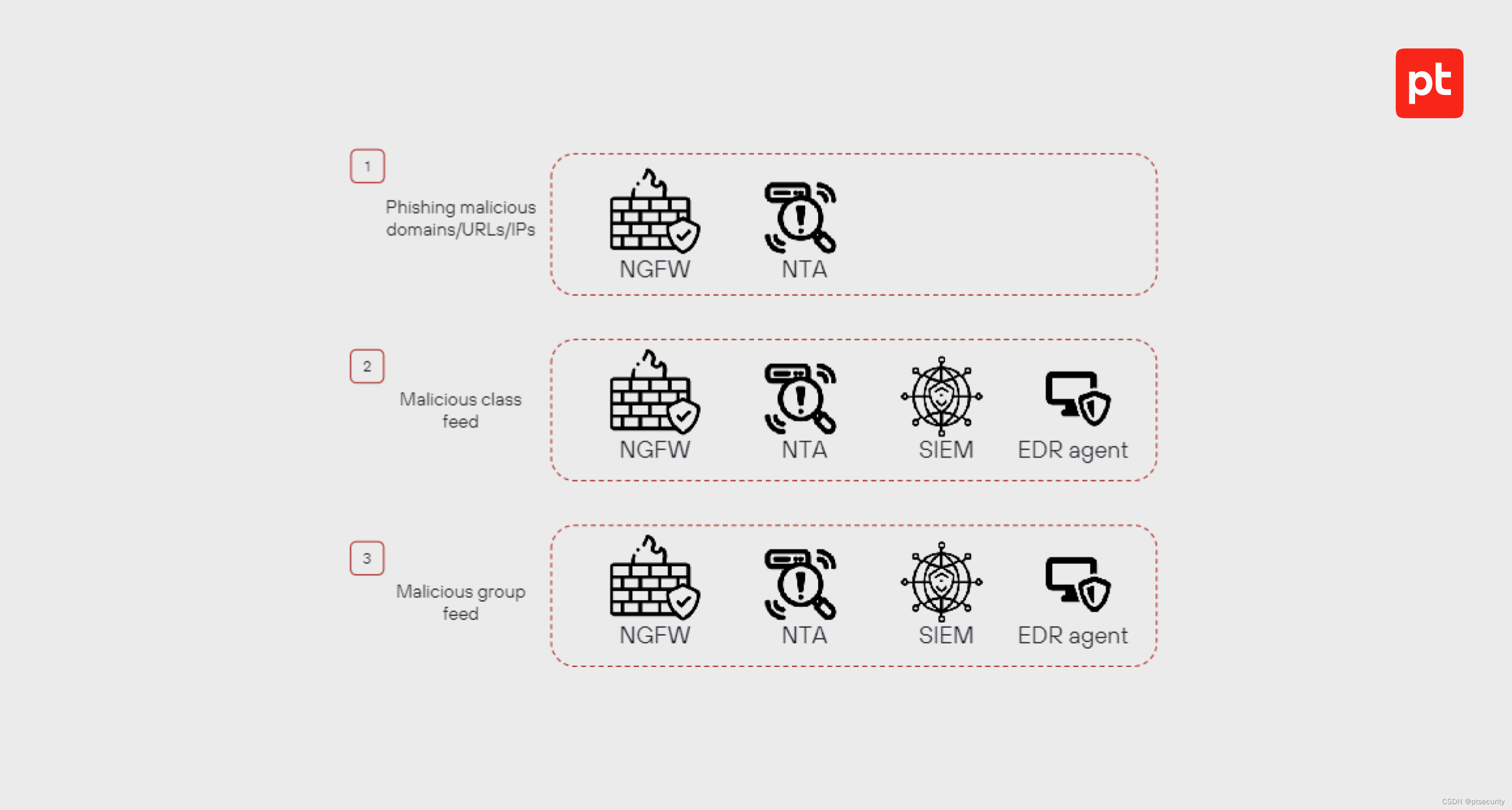
网络安全系统中的守护者:如何借助威胁情报 (TI) 提高安全性
在这篇哈巴尔网站上的推文中,我们将解释 TI 缩写背后的含义、为什么需要它、Positive Technologies 收集哪些网络威胁数据以及如何帮助企业预防网络威胁。我们将以四种情况为例,说明公司如何使用 PT Threat Intelligence Feeds 来发现恶意活动并预防攻击…...

并发编程 - CompletableFuture
文章目录 Pre概述FutureFuture的缺陷类继承关系功能概述API提交任务的相关API结果转换的相关APIthenApplyhandlethenRunthenAcceptthenAcceptBoththenCombinethenCompose 回调方法的相关API异常处理的相关API获取结果的相关API DEMO实战注意事项 Pre 每日一博 - Java 异步编程…...

IPIDEA参展ChinaJoy!探索未来创新科技的峰会之旅
中国最大的国际数码互动娱乐展会ChinaJoy即将于7月28日在上海举行,届时将聚集全球来自22个国家和地区的领先科技公司、创业者和技术专家,为参观者呈现一系列引人入胜的展览和活动。而IPIDEA作为参展商之一,将为参观者带来一场关于数字科技的奇…...

2023最新ChatGPT商业运营版网站源码+支持ChatGPT4.0+GPT联网+支持ai绘画(Midjourney)+支持Mind思维导图生成
本系统使用Nestjs和Vue3框架技术,持续集成AI能力到本系统! 支持GPT3模型、GPT4模型Midjourney专业绘画(全自定义调参)、Midjourney以图生图、Dall-E2绘画Mind思维导图生成应用工作台(Prompt)AI绘画广场自定…...
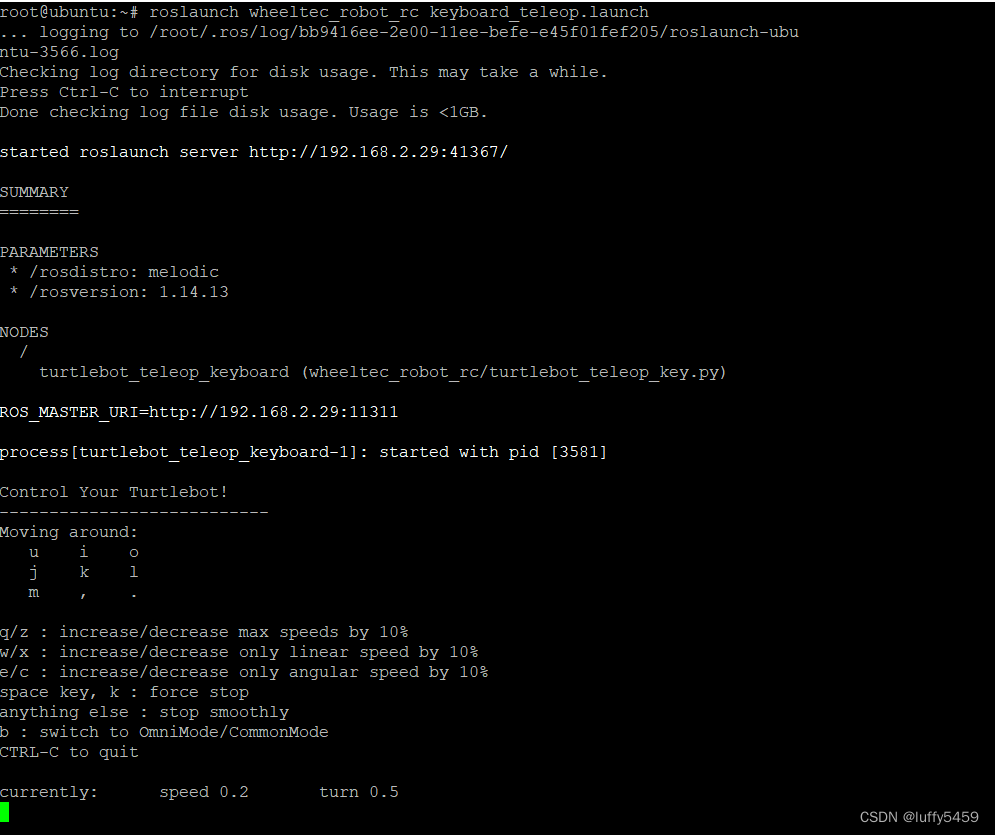
轮趣科技教育版ros小车键盘控制运动
我之前买的ros小车是单独买的底板,以为随便一个树莓派就可以,因为我以前有一个树莓派3B,后来买了单独的小车之后,发现只能使用树莓派4B,然后又单独买了一个树莓派4B,给装上镜像,安装ros-melodic…...
方法)
深入理解Python中的os.chdir()方法
深入理解Python中的os.chdir()方法 1. 简介 在Python中,os.chdir()方法用于改变当前的工作目录。工作目录是指当前正在执行的脚本所在的目录。通过使用os.chdir()方法,我们可以在脚本执行过程中切换到不同的目录。 在编写Python脚本时,我们…...

【Golang 接口自动化02】使用标准库net/http发送Post请求
目录 写在前面 发送Post请求 示例代码 源码分析 Post请求参数解析 响应数据解析 验证 发送Json/XMl Json请求示例代码 xml请求示例代码 总结 资料获取方法 写在前面 上一篇我们介绍了使用 net/http 发送get请求,因为考虑到篇幅问题,把Post单…...
LaTex语法(常用数学符号的语法和注意事项)
说明:[]括号表示把语法括起来,并不表示LaTex语法。 1. 求和符号(Σ) 这个符号的基本语法为:[\sum_{}^{}]。 符号有两种模式:内联数学模式(inside math mode)和显示数学模式(displayed math mode)。 内联数学模式:排版时使用各…...
Yunfly 一款高效、性能优异的node.js企业级web框架
介绍 Yunfly 一款高性能 Node.js WEB 框架, 使用 Typescript 构建我们的应用。 使用 Koa2 做为 HTTP 底层框架, 使用 routing-controllers 、 typedi 来高效构建我们的 Node 应用。 Yunfly 在 Koa 框架之上提升了一个抽象级别, 但仍然支持 Koa 中间件。在此基础之上, 提供了一…...

mac m1安装Centos9
先看结果(在mac M1 安装centos8 安装不成功的原因大部分是没有找到正确的系统) 由于Cnetos8 停服,现有mac m1 上能够按照的Centos8 并非由官方发布,因此寻找官方发布的能够在mac m1上安装的centos版本。 在YouTuBe上找到一个视频…...

深入理解mAP
0 介绍 mAP是目标检测任务最重要的评价指标。 mAP 是mean average precosion的缩写,mean 和 average都是平均的意思, 所以这个指标的计算涉及到2次平均。 mean是对所有类别的平均, 比如VOC 数据有20个类, 每个类别分别计算AP&…...

PostGis -基础、Springboot 整合、电子围栏处理
目的: 为什么要用PostgreSQL? 因为有时候我们需要存储 空间数据,如:存储一个 多边形 到数据。PostGis中 geometry、geography :基本空间数据类型,用于表达点线面等空间要素,具体类型涵盖了OGC的简单对象模…...
【Linux】多线程的补充
1 线程安全的单例模式 1.1 什么是单例模式 单例模式是一种 "经典的, 常用的, 常考的" 设计模式. 1.2 什么是设计模式 IT行业这么火, 涌入的人很多. 俗话说林子大了啥鸟都有. 大佬和菜鸡们两极分化的越来越严重. 为了让菜鸡们不太拖大佬的后腿, 于是大佬们针对一些…...
【MySQL】表的操作
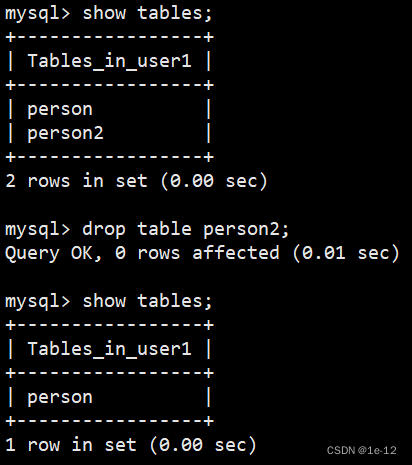
今天我们来谈谈MySQL下对表的操作 目录 一、创建表 二、查看表 2.1 查看库中存有的表 2.2 查看表结构 2.3 查看表的创建语句 三、修改表 3.1 重命名表名 3.2 新增列 3.3 修改列的数据类型 3.4 删除列 3.5 重命名列 3.6 向表中插入数据 四、删除表 一、创建表 我…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
