25.9 matlab里面的10中优化方法介绍—— 惩罚函数法求约束最优化问题(matlab程序)
1.简述
一、算法原理
1、问题引入
之前我们了解过的算法大部分都是无约束优化问题,其算法有:黄金分割法,牛顿法,拟牛顿法,共轭梯度法,单纯性法等。但在实际工程问题中,大多数优化问题都属于有约束优化问题。惩罚函数法就可以将约束优化问题转化为无约束优化问题,从而使用无约束优化算法。
2、约束优化问题的分类
约束优化问题大致分为三类:等式约束、不等式约束、等式+不等式约束。
其数学模型为:
等式约束
s.t hv(x)=0,v=1,2,...,p<n
等式约束
s.t
等式+不等式约束问题
s.t hv(x)=0,v=1,2,...,p<n
3、惩罚函数法定义
惩罚函数法(SUMT法)又称序列无约束极小化技术,将等式约束与不等式约束的条件,经过适当定义的复合函数加到原目标函数上构造了惩罚函数,从而取消了约束,转而求解一系列无约束优化问题。
按照惩罚函数再优化过程中的迭代点是否在约束条件的可行域内,又分为内点法、外点法和混合法
内点法:迭代点再约束条件的可行域之内,只用于不等式约束。
外点法:迭代点再约束条件的可行域之外,既用于不等式约束又可用于等式约束。
4、外点惩罚函数法
等式约束:
s.t h1(x)=x1−2=0,h2(x)=x2+3=0
算法步骤
a、构造惩罚函数:F=f+M * { [ h1(x) ]^2 + [ h2(x) ]^2 } ,式中M为初始惩罚因子;
b、然后用无约束优化极值算法求解(牛顿法);
c、 如果相邻两次惩罚函数无约束最优点之间的距离足够小【norm(x1-x0)<eps】,则收敛;
否则放大惩罚因子M=C*M,式中C为 罚因子放大系数;
d、转步骤a继续迭代;
2.代码
主程序:
clear
f ='f1209';
x0=[3 0];
TolX = 1e-4;
TolFun = 1e-9;
MaxIter=100;
alpha0 = 1;
%%%%选用不是基于梯度的无约束最优化方法求解,的正确结果
[xo_Nelder,fo_Nelder] = Opt_Nelder(f,x0,TolX,TolFun,MaxIter) %Nelder 方法
[fc_Nelder,fo_Nelder,co_Nelder] = f1209(xo_Nelder) %Nelder方法结果
[xo_s,fo_s] = fminsearch(f,x0) %MATLAB 内置函数fminsearch()
[fc_s,fo_s,co_s] = f1209(xo_s) %相应的结果
%%%基于梯度的方法最速下降法等,得到错误结果
grad=inline('[2*(x(1)+1)*((x(1)-1.2)^2+0.4*(x(2)-0.5)^2)+((x(1)+1)^2+4*(x(2)-1.5)^2)*2*(x(1)-1.2),8*(x(2)-1.5)*((x(1)-1.2)^2+0.4*(x(2)-0.5)^2)+((x(1)+1)^2+4*(x(2)-1.5)^2)*0.8*(x(2)-0.5)]','x');
xo_steep = Opt_Steepest(f,grad,x0,TolX,TolFun,alpha0) %最速下降法
[fc_steep,fo_steep,co_steep] = f1209(xo_steep) %相应结果
[xo_u,fo_u] = fminunc(f,x0); % MATLAB 内置函数fminunc()
[fc_u,fo_u,co_u] = f1209(xo_u) %相应结果
子程序:
function [xo,fo] =Opt_Nelder(f,x0,TolX,TolFun,MaxIter)
%Nelder-Mead法用于多维变量的最优化问题,维数>=2.
N = length(x0);
if N == 1 %一维情况,用二次逼近计算
[xo,fo] = Opt_Quadratic(f,x0,TolX,TolFun,MaxIter);
return
end
S = eye(N);
for i = 1:N %自变量维数大于2时,重复计算每个子平面的情况
i1 = i + 1;
if i1 > N
i1 = 1;
end
abc = [x0; x0 + S(i,:); x0 + S(i1,:)]; %每一个定向子平面
fabc = [feval(f,abc(1,:)); feval(f,abc(2,:)); feval(f,abc(3,:))];
[x0,fo] = Nelder0(f,abc,fabc,TolX,TolFun,MaxIter);
if N < 3 %二维情况不需重复
break;
end
end
xo = x0;
3.运行结果
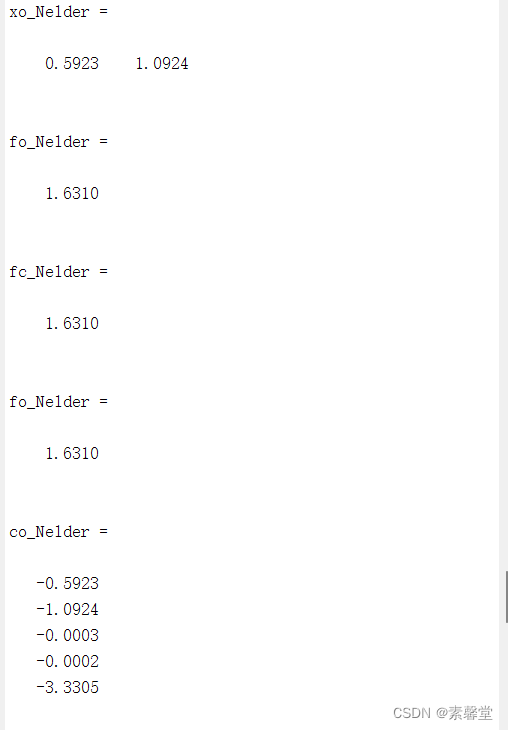

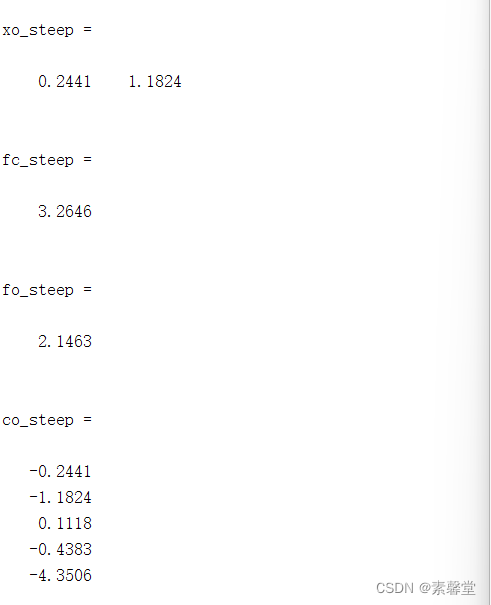

相关文章:

25.9 matlab里面的10中优化方法介绍—— 惩罚函数法求约束最优化问题(matlab程序)
1.简述 一、算法原理 1、问题引入 之前我们了解过的算法大部分都是无约束优化问题,其算法有:黄金分割法,牛顿法,拟牛顿法,共轭梯度法,单纯性法等。但在实际工程问题中,大多数优化问题都属于有约…...

django channels实战(websocket底层原理和案例)
1、websocket相关 1.1、轮询 1.2、长轮询 1.3、websocket 1.3.1、websocket原理 1.3.2、django框架 asgi.py在django项目同名app目录下 1.3.3、聊天室 django代码总结 小结 1.3.4、群聊(一) 前端代码 后端代码 1.3.5、群聊(二)…...
学习使用axios,绑定动态数据
目录 axios特性 案例一:通过axios获取笑话 案例二:调用城市天气api接口数据实现天气查询案例 axios特性 支持 Promise API 拦截请求和响应(可以在请求前及响应前做某些操作,例如,在请求前想要在这个请求头中加一些…...
c语言内存函数的深度解析
本章对 memcpy,memmove,memcmp 三个函数进行详解和模拟实现; 本章重点:3个常见内存函数的使用方法及注意事项并学会模拟实现; 如果您觉得文章不错,期待你的一键三连哦,你的鼓励是我创作的动力…...

低代码平台介绍(国内常见的)
文章目录 前言1、阿里云宜搭2、腾讯云微搭3、百度爱速搭4、华为云Astro轻应用 Astro Zero(AppCube)5、字节飞书多维表格6、云程低代码平台7、ClickPaaS8、网易轻舟9、用友YonBuilder10、金蝶苍穹云平台11、泛微平台12、蓝凌低代码平台13、简道云14、轻流…...
matlab RRR机械臂 简略代码
RRR机器人!启动! gazebo在arm mac上似乎难以运行,退而选择Matlab,完成老师第一个作业,现学现卖,权当记录作业过程,有不足之处,多多指教。 作业!启动! RRR机…...

集成测试,单元测试隔离 maven-surefire-plugin
详见 集成测试,单元测试隔离 maven-surefire-plugin maven的goal生命周期 Maven生存周期 - 含 integration-test Maven本身支持的命令(Goals)是有顺序的,越后面执行的命令,会将其前面的命令和其本身按顺序执行一遍,…...
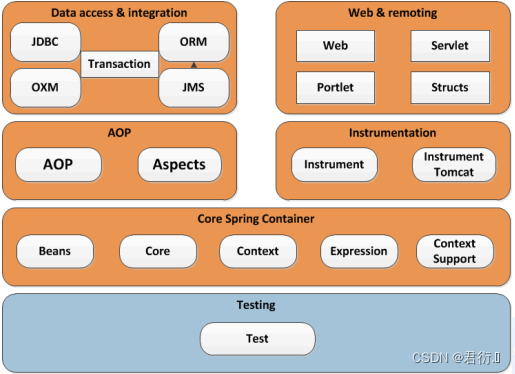
渗透测试基础知识(1)
渗透基础知识一 一、Web架构1、了解Web2、Web技术架构3、Web客户端技术4、Web服务端组成5、动态网站工作过程6、后端存储 二、HTTP协议1、HTTP协议解析2、HTTP协议3、http1.1与http2.0的区别4、HTTP协议 三、HTTP请求1、发起HTTP请求2、HTTP响应与请求-HTTP请求3、HTTP响应与请…...

Android NDK开发
工程目录图 NDK中文官网 请点击下面工程名称,跳转到代码的仓库页面,将工程 下载下来 Demo Code 里有详细的注释 代码:TestNDK 参考文献 Android NDK 从入门到精通(汇总篇)Android JNI(一)——NDK与JNI基础Android之…...

使用python爬取淘宝商品信息
要使用Python爬取淘宝商品信息,您可以按照以下步骤: 安装必要的库 您需要安装Python的requests库和BeautifulSoup库。 要使用Python爬取淘宝商品信息,您可以按照以下步骤:安装必要的库 您需要安装Python的requests库和Beautifu…...
)
QEMU源码全解析18 —— QOM介绍(7)
接前一篇文章:QEMU源码全解析17 —— QOM介绍(6) 本文内容参考: 《趣谈Linux操作系统》 —— 刘超,极客时间 《QEMU/KVM》源码解析与应用 —— 李强,机械工业出版社 特此致谢! 上一回完成了对…...

【华为OD机试】 选修课
题目描述 现有两门选修课,每门选修课都有一部分学生选修,每个学生都有选修课的成绩,需要你找出同时选修了两门选修课的学生,先按照班级进行划分,班级编号小的先输出,每个班级按照两门选修课成绩和的降序排序…...

225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。 实现 MyStack 类: void push(int x) 将元素 x 压入栈顶。 int pop() 移除并返回栈顶元素。 int to…...
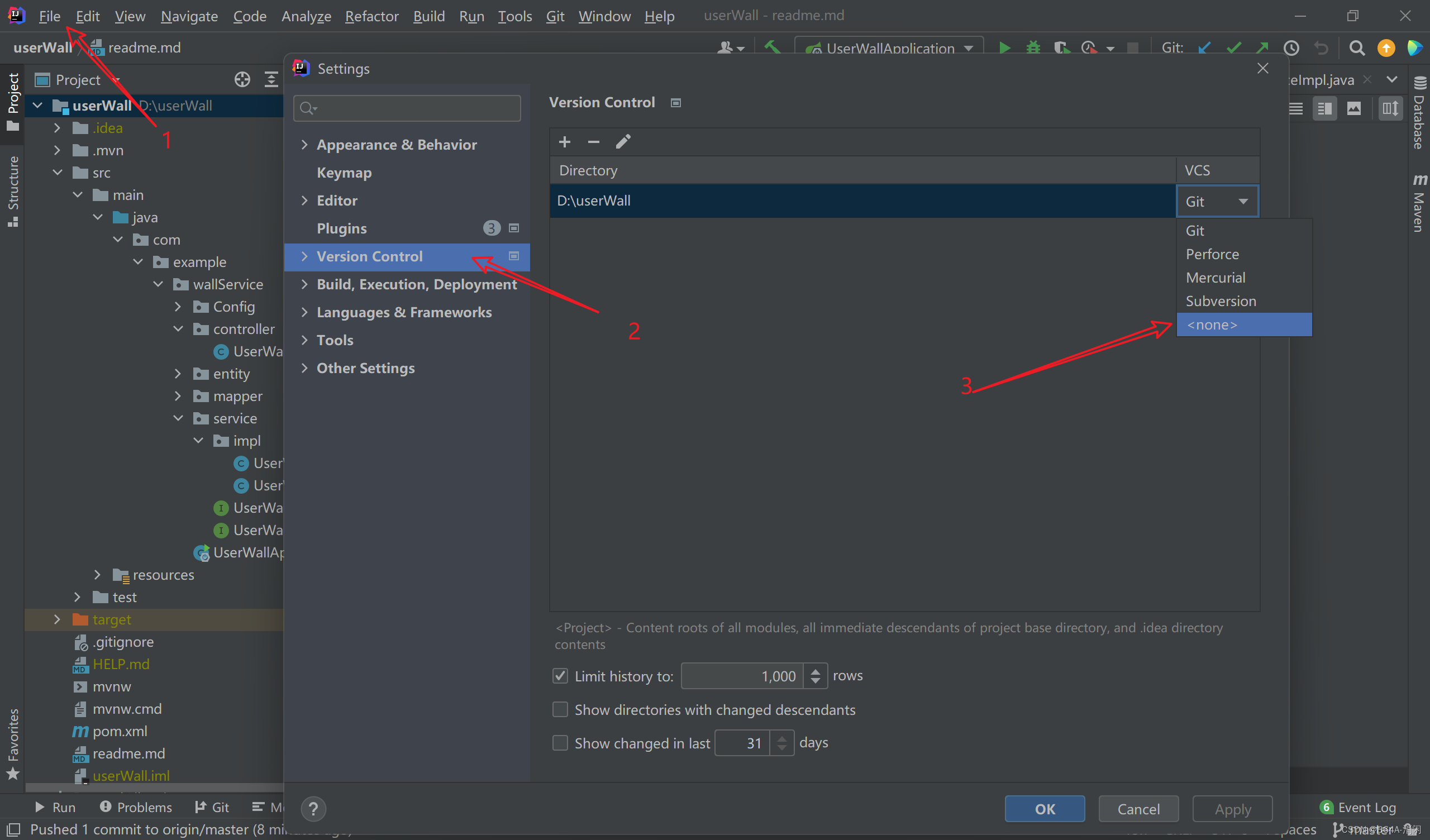
IDEA将本地项目上传到码云
一、创建本地仓库并关联 用IDEA打开项目,在菜单栏点击vcs->create git repository创建本地仓库, 选择当前项目所在的文件夹当作仓库目录。 二、将项目提交本地仓库 项目名右键就会出现“GIT”这个选项->Add->Commit Directory, 先将项目add…...
Ubuntu更改虚拟机网段(改成桥接模式无法连接网络)
因为工作需要,一开始在安装vmware和虚拟机时,是用的Nat网络。 现在需要修改虚拟机网段,把ip设置成和Windows端同一网段,我们就要去使用桥接模式。 环境: Windows10、Ubuntu20.04虚拟机编辑里打开虚拟网络编辑器&#…...
谷粒商城第七天-商品服务之分类管理下的删除、新增以及修改商品分类
目录 一、总述 1.1 前端思路 1.2 后端思路 二、前端部分 2.1 删除功能 2.2 新增功能 2.3 修改功能 三、后端部分 3.1 删除接口 3.2 新增接口 3.3 修改接口 四、总结 一、总述 1.1 前端思路 删除和新增以及修改的前端无非就是点击按钮,就向后端发送请求…...
Redis学习路线(1)—— Redis的安装
一、NoSQL SQL VS NoSQL 1、名称 SQL 主要是指关系数据库。NoSQL 主要是指非关系数据库。 2、存储结构 SQL 是结构化的数据库,以表格的形式存储数据。NoSQL 是非结构化的数据库,以Key-Value(Redis),JSON格式文档&…...
)
《MySQL 实战 45 讲》课程学习笔记(五)
数据库锁:全局锁、表锁和行锁 根据加锁的范围,MySQL 里面的锁大致可以分成全局锁、表级锁和行锁三类。 全局锁 全局锁就是对整个数据库实例加锁。 MySQL 提供了一个加全局读锁的方法,命令是 Flush tables with read lock (FTWRL)。当你需要…...

使用GADL对高程数据进行填洼
对于DEM数据中存在的洼地(sink)问题,可以使用GADL(Geospatial Data Abstraction Library)中的功能进行填洼操作。GADL是一个开源的GIS库,提供了许多对地理空间数据进行处理和分析的功能。 下面是使用GADL对…...
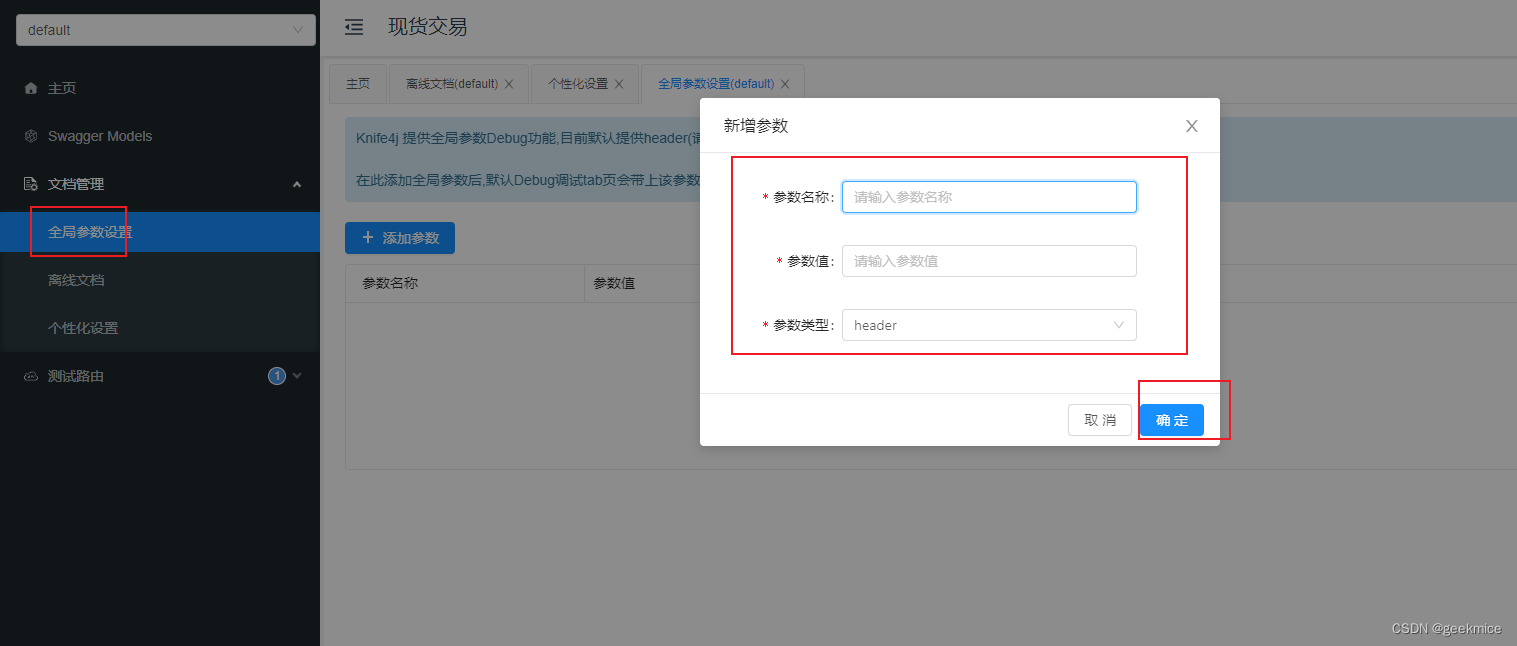
Spring Boot集成Swagger3.0,Knife4j导出文档
文章目录 Spring Boot集成Swagger3.0,Knife4j导出文档效果展示如何使用简要说明添加依赖添加配置类测试接口token配置位置 官网 说明情况 demo Spring Boot集成Swagger3.0,Knife4j导出文档 效果展示 如何使用 简要说明 Knife4j的前身是swagger-bootstrap-ui,前身swagger-boo…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
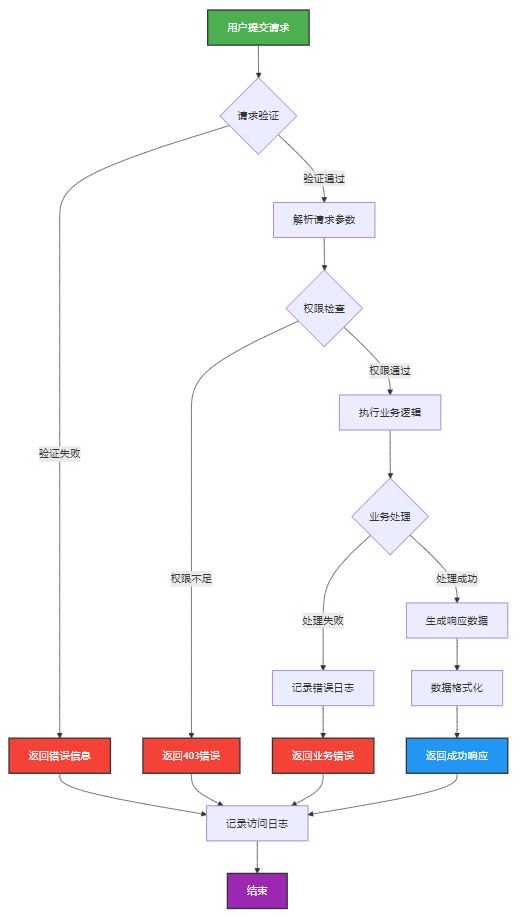
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...
