电子技术——内部电容效应以及MOS与BJT的高频响应模型
电子技术——内部电容效应以及MOS与BJT的高频响应模型

耦合和旁路电容决定了放大器的低频响应,同时内部电容效应决定了放大器的高频响应。本节,我们简单简单介绍一下内部电容效应,并且更重要的是如何在小信号模型中模型化内部电容效应。
MOSFET
在我们之前学习MOSFET的时候,我们就已经知道MOS中存在内部电容。实际上,我们已经在使用栅极和沟道之间的内部电容,即场效应。之前,我们假设MOS中的电容都是稳态的,也就是我们忽略了电容的充电和放电时间。结果就是我们并没有考虑电容的任何频率效应。实际上,MOSFET放大器在高频的时候增益会有所减小。同样的,在之后数字电路的章节,我们会学习MOS数字逻辑反相器会显示出有限的传播延迟。为了考虑这些情况,我们必须把内部电容考虑进去。这就是本节我们要讨论的。
为了说明产生内部电容的物理原因,我们使用下面的图片:
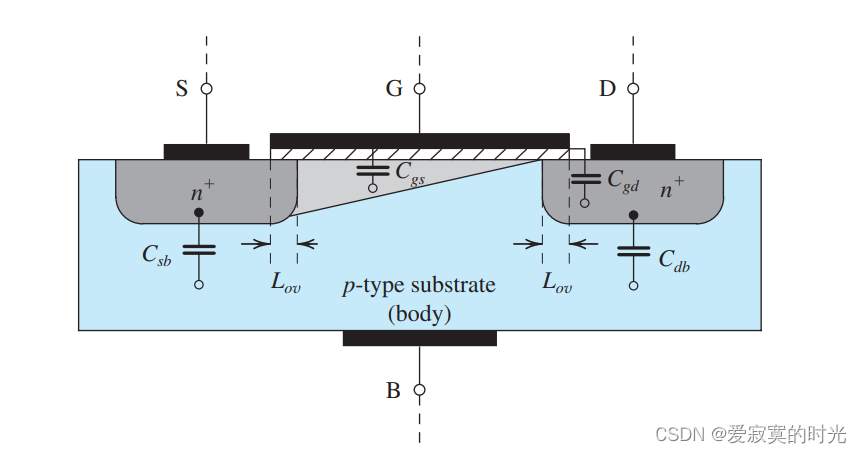
上图是一个N沟道的MOSFET,并且处于饱和区。如图,存在四个电容。其中两个 CgsC_{gs}Cgs 和 CgdC_{gd}Cgd 通过栅极电容效应形成,另外两个 CsbC_{sb}Csb 和 CdbC_{db}Cdb 是pn结的耗散区电容。
之前我们介绍过栅极电容,其中的硅氧化物层充当电介质,金属极板和沟道形成一个平行板电容器,每单位面积的容值记为 CoxC_{ox}Cox 。当MOS处于饱和区的时候,我们知道总容值是 23WLCox\frac{2}{3} WL C_{ox}32WLCox 。除此之外,因为极板与源极区和栅极区分别有一个小的重叠面积,重叠长度为 LovL_{ov}Lov ,则重叠部分的电容为:
Cov=WLovCoxC_{ov} = WL_{ov} C_{ox} Cov=WLovCox
一般的, Lov=0.05L∼0.1LL_{ov} = 0.05L \sim 0.1LLov=0.05L∼0.1L 。现在我们能表示出栅极到源极直接的电容为:
Cgs=23WLCox+CovC_{gs} = \frac{2}{3} WLC_{ox} + C_{ov} Cgs=32WLCox+Cov
对于栅极到漏极之间的电容,我们注意到沟道被截断,所以电容只由重叠部分组成:
Cgd=CovC_{gd} = C_{ov} Cgd=Cov
对于耗散层的电容,可以使用我们之前推导的反向偏置pn结中的电容表达式:
Csb=Csb01+VSBV0C_{sb} = \frac{C_{sb0}}{\sqrt{1 + \frac{V_{SB}}{V_0}}} Csb=1+V0VSBCsb0
其中 Csb0C_{sb0}Csb0 是在体极和源极之间无偏置时候的电容值, VSBV_{SB}VSB 是反向偏置电压的大小, V0V_0V0 是pn结内建电压(0.6V 到 0.8V),同样的对于体极和漏极之间的电容:
Cdb=Cdb01+VDBV0C_{db} = \frac{C_{db0}}{\sqrt{1 + \frac{V_{DB}}{V_0}}} Cdb=1+V0VDBCdb0
我们发现,对于两个电容的过度系数均为 m=1/2m = 1/2m=1/2 。
值得注意的是,每一个结电容都是由耗散区的底部和周围的三个面(第四个面向沟道)分别贡献而成。上述表达式都是建立在小信号模型的表达式上。
MOSFET的高频模型
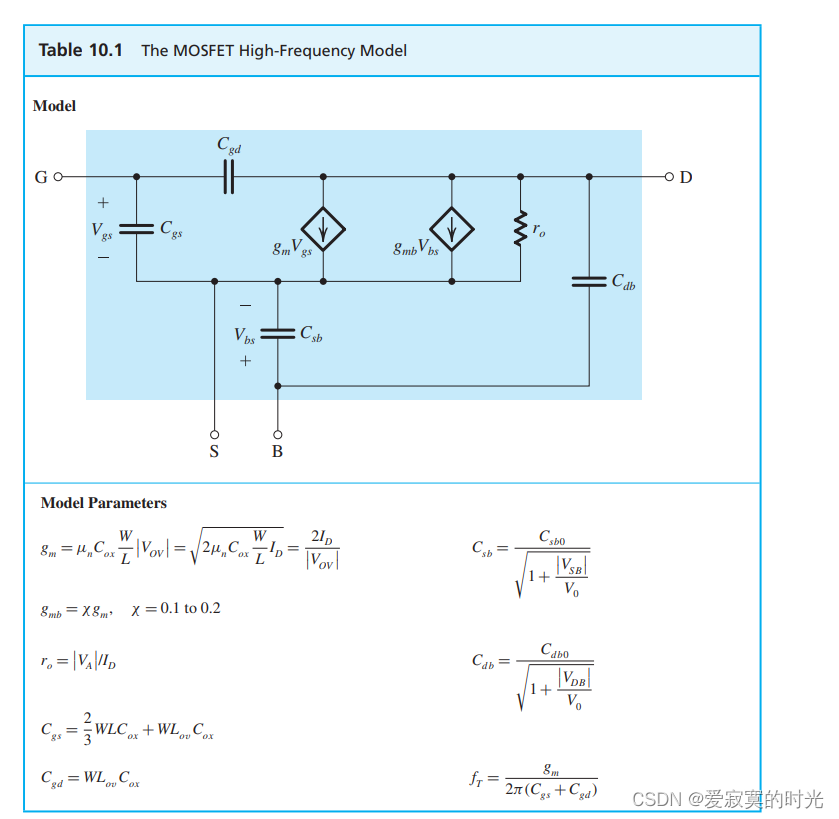
下图展示了MOSFET的高频模型,其中包括我们介绍的四个电容:

这个模型可以用来计算MOS放大器的高频响应,然而这个模型实在是太复杂了,不管是对于手动分析还是计算机仿真分析来说。幸运的是,如果体极和源极是相连的,我们的模型可以大大简化:
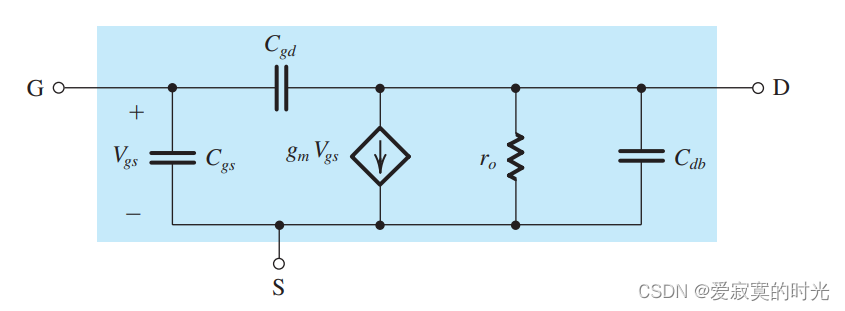
在这个模型中, CgdC_{gd}Cgd 尽管很小,但是对于决定高频响应有至关重要的作用,不能忽略。但是电容 CdbC_{db}Cdb 在高频响应分析中基本可以忽略,忽略之后的模型如下:

最后对应的T模型为:
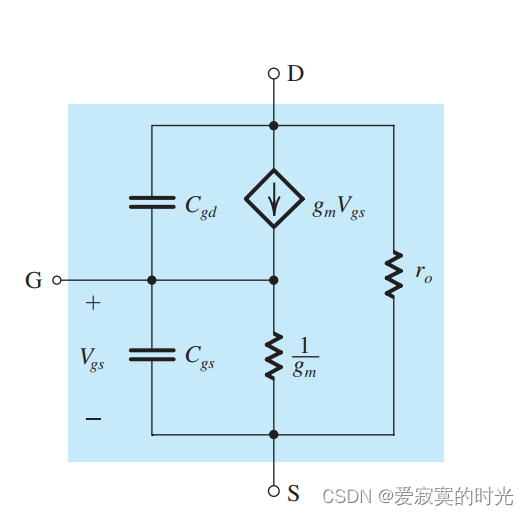
MOS的单位增益频率
对于MOS放大器来说,有一个重要的参数就是单位增益频率 fTf_TfT ,也称为 过度频率 。定义为CS放大器配置时的短路电流是单位电流增益时候的频率。下图展示了一个CS放大器的混合 π\piπ 模型。为了决定短路电流增益,我们在输入端放入测试电流源 IiI_iIi ,并且短路输出端:
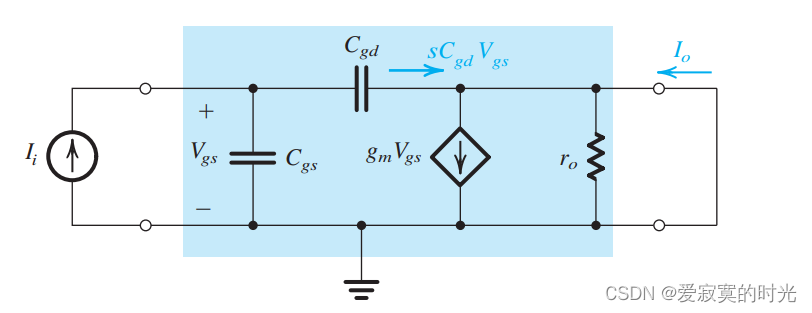
通过简单的计算得出,输出电流为:
Io=gmVgs−sCgdVgsI_o = g_mV_{gs} - sC_{gd}V_{gs} Io=gmVgs−sCgdVgs
回想一下 CgdC_{gd}Cgd 非常小,我们可以忽略第二项:
Io≃gmVgsI_o \simeq g_m V_{gs} Io≃gmVgs
我们可以导出 VgsV_{gs}Vgs :
Vgs=Iis(Cgs+Cgd)V_{gs} = \frac{I_i}{s(C_{gs} + C_{gd})} Vgs=s(Cgs+Cgd)Ii
则电流比为:
IoIi=gms(Cgs+Cgd)\frac{I_o}{I_i} = \frac{g_m}{s(C_{gs} + C_{gd})} IiIo=s(Cgs+Cgd)gm
带入物理频率 s=jωs = j \omegas=jω 得到:
∣IoIi∣=gmω(Cgs+Cgd)|\frac{I_o}{I_i}| = \frac{g_m}{\omega(C_{gs} + C_{gd})} ∣IiIo∣=ω(Cgs+Cgd)gm
则单位增益时候的频率是在:
ωT=gm/(Cgs+Cgd)\omega_T = g_m / (C_{gs} + C_{gd}) ωT=gm/(Cgs+Cgd)
或是:
fT=gm2π(Cgs+Cgd)f_T = \frac{g_m}{2\pi (C_{gs} + C_{gd})} fT=2π(Cgs+Cgd)gm
因为 fTf_TfT 正比于 gmg_mgm ,并且 gmg_mgm 决定了中频带的增益。反比与 (Cgs+Cgd)(C_{gs} + C_{gd})(Cgs+Cgd) 限制了放大器的带宽, fTf_TfT 的值越大,MOS的频率效率就越好。
一般的, fTf_TfT 对于旧技术(5um COMS)来说在100MHz,对于高速新技术(0.13um COMS)在几GHz。
总结
BJT
与MOS同样的,BJT也存在内部电容效应。
基极充电或扩散电容 CdeC_{de}Cde
当BJT工作在主动模式下,次载流子充满基极区域。对于npn晶体管,基极区域充满了电子,我们记电荷量 QnQ_nQn 可以表示为:
Qn=τFiCQ_n = \tau_F i_C Qn=τFiC
其中 iCi_CiC 是集电极电流, τF\tau_FτF 是器件的时间常数,具有时间量纲,被称为 前向基极-过渡时间 ,表示一个次载流子(电子)通过基极区域的平均时间。一般情况下,在 10ps 到 100ps。
上式是一个大信号模型,因为 iCi_CiC 与 vBEv_{BE}vBE 呈现指数关系,同时 QnQ_nQn 也同样依赖于 vBEv_{BE}vBE 。对于小信号模型,我们定义 小信号扩散电容 :
Cde≡dQndvBE=τFdiCdvBE=τFgm=τFICVTC_{de} \equiv \frac{d Q_n}{d v_{BE}} = \tau_F \frac{d i_C}{d v_{BE}} = \tau_F g_m = \tau_F \frac{I_C}{V_T} Cde≡dvBEdQn=τFdvBEdiC=τFgm=τFVTIC
这里 ICI_CIC 是集电极偏置电流。因此当 vbev_{be}vbe 改变 vBEv_{BE}vBE 的时候,发射极电流增加 gmvbeg_m v_{be}gmvbe 因此电荷量增加 τFgmvbe\tau_F g_m v_{be}τFgmvbe 多出来的电荷由基极电流提供。
基极-发射极结电容 CjeC_{je}Cje
在BJT的主动模式下,基极和发射极直接存在电容 CjeC_{je}Cje ,我们知道,正向偏置的pn的电容为:
Cje≃2Cje0C_{je} \simeq 2C_{je0} Cje≃2Cje0
这里 Cje0C_{je0}Cje0 是零偏置下的电容。
集电极-基极结电容 CμC_\muCμ
在在BJT的主动模式下,集电极-基极是一个反向偏置的pn结,我们称其为 耗散电容 ,其值为:
Cμ=Cμ0(1+VCBV0c)mC_\mu = \frac{C_{\mu0}}{(1 + \frac{V_{CB}}{V_{0c}})^m} Cμ=(1+V0cVCB)mCμ0
这里 Cμ0C_{\mu0}Cμ0 是无偏置下的电容。 VCBV_{CB}VCB 是反向电压, V0cV_{0c}V0c 是内建电压(0.75V), mmm 是过渡系数(0.2-0.5)。
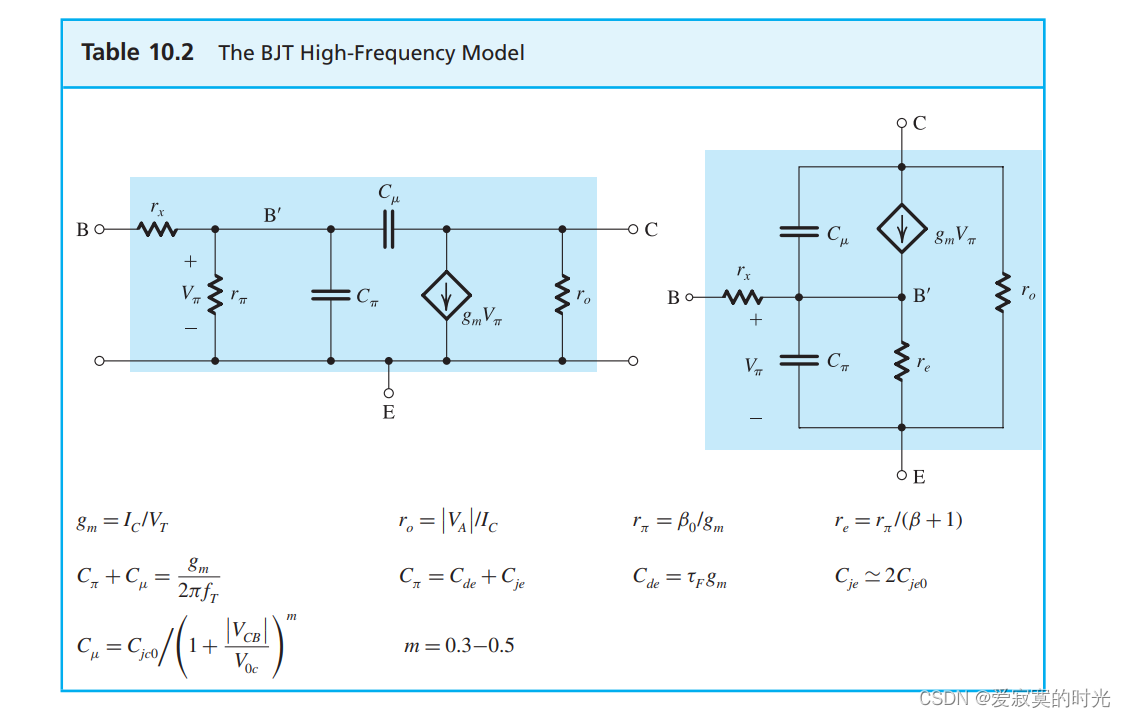
高频模型
下图展示了BJT的混合 π\piπ 和T模型下的高频模型。
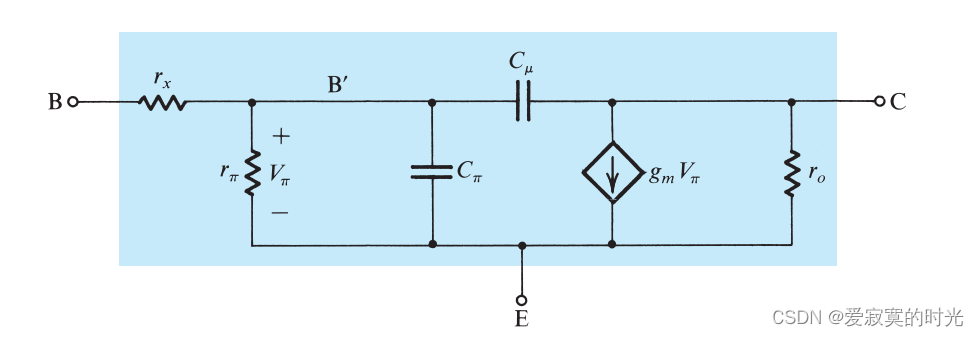
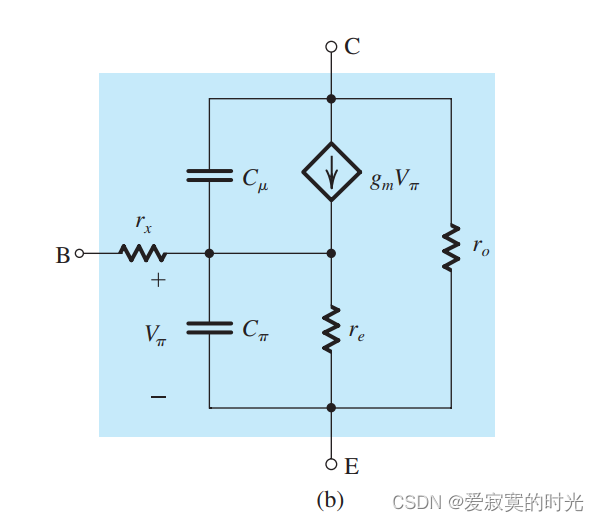
在图中,分别有两个电容,一个是发射极到基极的电容:
Cπ=Cde+CjeC_\pi = C_{de} + C_{je} Cπ=Cde+Cje
另一个是集电极到基极的电容 CμC_\muCμ 。除此之外,我们还添加了基极的固有电阻 rxr_xrx 在外部基极B和内部基极B‘之间,因为 rx≪rπr_x \ll r_\pirx≪rπ 因此在低频模型下,我们可以忽略,但是在高频模型下,这个电阻是通过电流的并且和电容相互作用,就无法忽略。
BJT的单位增益频率
在datasheet中通常不直接给出 CπC_\piCπ 而是给出 β\betaβ 与频率之间的关系。为了决定 CπC_\piCπ 和 CμC_\muCμ 我们需要导出与 β\betaβ 之间的关系。我们使用下面的CE短路电流:
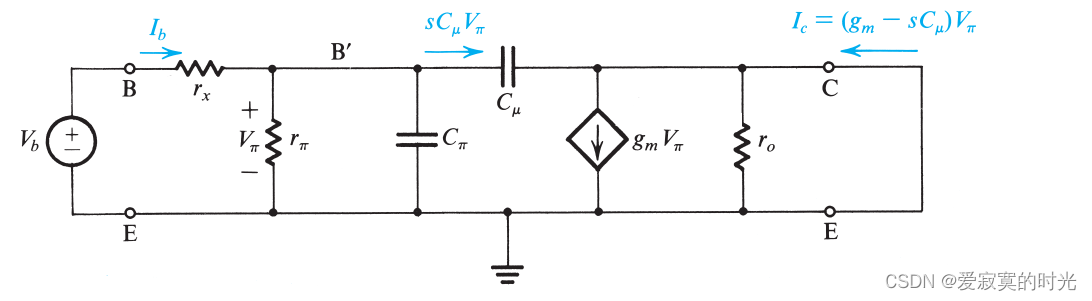
在节点C的电流为:
Ic=(gm−sCμ)VπI_c = (g_m -sC_\mu)V_\pi Ic=(gm−sCμ)Vπ
这里 VπV_\piVπ 和 IbI_bIb 的关系为:
Vπ=Ib(rπ∣∣Cπ∣∣Cμ)V_\pi = I_b(r_\pi||C_\pi||C_\mu) Vπ=Ib(rπ∣∣Cπ∣∣Cμ)
则电流比为:
hfe=IcIb=gm−sCμ1/rπ+s(Cπ+Cμ)h_{fe} = \frac{I_c}{I_b} = \frac{g_m - sC_\mu}{1/r_\pi + s(C_\pi + C_\mu)} hfe=IbIc=1/rπ+s(Cπ+Cμ)gm−sCμ
在一定的频率下, ωCμ≪gm\omega C_\mu \ll g_mωCμ≪gm 因此:
hfe≃gmrπ1+s(Cπ+Cμ)rπ=β01+s(Cπ+Cμ)rπh_{fe} \simeq \frac{g_m r_\pi}{1 + s(C_\pi + C_\mu)r_\pi} = \frac{\beta_0}{1 + s(C_\pi + C_\mu)r_\pi} hfe≃1+s(Cπ+Cμ)rπgmrπ=1+s(Cπ+Cμ)rπβ0
这里的 β0\beta_0β0 为低频下的 β\betaβ 并且 hfeh_{fe}hfe 存在一个单极点频率,此时为 3dB3dB3dB 响应:
ωβ=1(Cπ+Cμ)rπ\omega_\beta = \frac{1}{(C_\pi +C_\mu)r_\pi} ωβ=(Cπ+Cμ)rπ1
下图展示了该电路的高频响应:
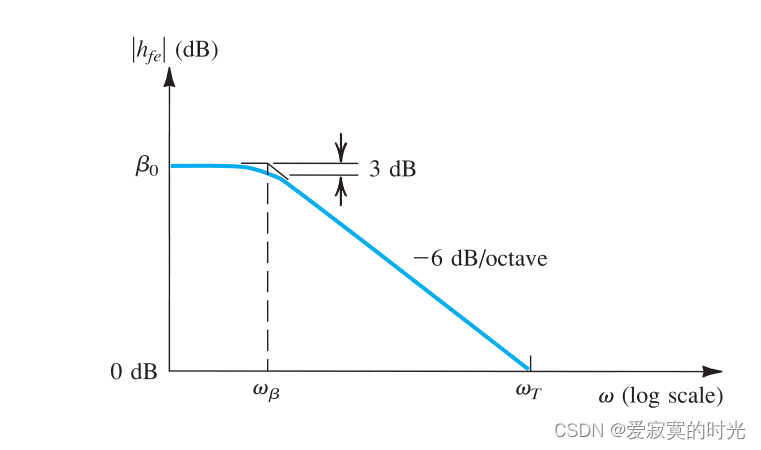
存在单位增益频率 ωT\omega_TωT :
ωT=β0ωβ=gmCπ+Cμ\omega_T = \beta_0 \omega_\beta = \frac{g_m}{C_\pi + C_\mu} ωT=β0ωβ=Cπ+Cμgm
fT=gm2π(Cπ+Cμ)f_T = \frac{g_m}{2\pi(C_\pi + C_\mu)} fT=2π(Cπ+Cμ)gm
这个形式和MOS的一致。
通常在datasheet中给出 fTf_TfT ,而 fTf_TfT 是一个关于偏置电流的参数:
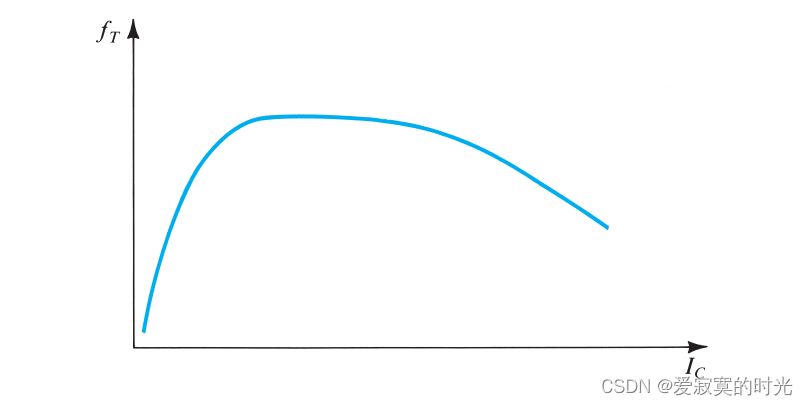
我们发现,在较低的偏置电流下,单位增益频率也较低。但是随着偏置电流继续加大,单位增益频率却降低了,此时不能使用上述表达式解释其原因,主要原因在 β0\beta_0β0 在大电流的情况下会下降。在 fTf_TfT 的常数区域,CπC_\piCπ 主要由扩散部分组成且远大于 CμC_\muCμ 因此 Cπ+Cμ≃Cde=τFgmC_\pi + C_\mu \simeq C_{de} = \tau_Fg_mCπ+Cμ≃Cde=τFgm :
fT=12πτFf_T = \frac{1}{2 \pi \tau_F} fT=2πτF1
一般情况下,fTf_TfT 在 100MHz到几十GHz。
关于高频模型,当频率处于 5∼10fβ5 \sim 10 f_\beta5∼10fβ 的时候,我们可以忽略 rπr_\pirπ 此时的阻抗由 rxr_xrx 决定。因此在高频模型下 rxr_xrx 具有关键作用。
在结束本节之前,我们应该注意到在高频模型下,BJT能够精准的工作直到 0.2fT0.2f_T0.2fT 。若想获得更大的 fTf_TfT 需要往BJT模型中加入更多的寄生元件。
总结
相关文章:

电子技术——内部电容效应以及MOS与BJT的高频响应模型
电子技术——内部电容效应以及MOS与BJT的高频响应模型 耦合和旁路电容决定了放大器的低频响应,同时内部电容效应决定了放大器的高频响应。本节,我们简单简单介绍一下内部电容效应,并且更重要的是如何在小信号模型中模型化内部电容效应。 MOS…...
)
华为OD机试题 - 出租车计费(JavaScript)
最近更新的博客 2023新华为OD机试题 - 斗地主(JavaScript)2023新华为OD机试题 - 箱子之形摆放(JavaScript)2023新华为OD机试题 - 考古学家(JavaScript)2023新华为OD机试题 - 相同数字的积木游戏 1(JavaScript)2023新华为OD机试题 - 最多等和不相交连续子序列(JavaScri…...
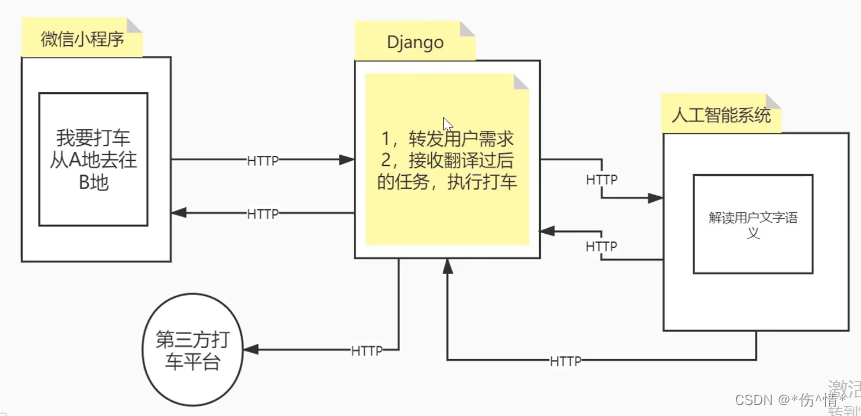
Django框架进阶版
一、Django介绍 1.起源 2005年发布,采用python语言编写的。 早期Django主要做新闻和内容管理 重量级python web框架,配备了大量组件 2.组件 包含组件如下 基本配置文件/路由系统 MTV设计模式 Cookies和Session 分页和发邮件 Admin管理后台 3…...
2023美赛F题全部代码+数据+结果 数学建模
2023年美赛F题全部思路 数据代码都已完成 全部内容见链接:https://www.jdmm.cc/file/2708700/ 1.根据文献选的GGDP的指标,发现GGDP与水资源等有关,由此可以筛选出影响GGDP的所有因子,并可以用所有因子利用层次分析法建立评价体…...

Java基础-logback日志使用
日志 1.1 作用: 跟输出语句一样,可以把程序在运行过程中的详细信息都打印在控制台上。 利用log日志还可以把这些详细信息保存到文件和数据库中。 1.2 使用步骤: 不是java的,也不是自己写的,是第三方提供…...

kaggle竞赛-宠物受欢迎程度(赛题讲解与数据分析)
比赛官网地址 赛题介绍 petfinder是马来西亚领先的动物福利平台宠物网站地址 该网站使用可爱指数来排名宠物照片。它分析了图片组成和其他因素,并与数千个宠物档案的表现进行了比较。 在这场比赛中,你将分析原始图像和元数据来预测宠物照片的“Pawp…...

Go语言基础知识学习笔记
环境准备 下载安装Golang:https://golang.google.cn/dl/ 因为国外下载速度较慢,我们需要配置国内代理 # 开启包管理工具 go env -w GO111MODULEon # 设置代理 go env -w GOPROXYhttps://goproxy.cn,direct # 设置不走 proxy 的私有仓库,多…...

Python3 错误和异常
Python3 错误和异常 作为 Python 初学者,在刚学习 Python 编程时,经常会看到一些报错信息,在前面我们没有提及,这章节我们会专门介绍。 Python 有两种错误很容易辨认:语法错误和异常。 Python assert(断…...

程序人生 - 学习和分享
文章目录记于 230217学习安排泛学AI 和 未来记于 230217 刚入行时,经常看到技术博客中,博主们分享生活,比如相亲、上班生活,甚至还有人发结婚照。这个栏目通常被称为:程序人生。 这个现象已经很久没看到了,…...

基于树莓派的智能家居项目整理
一、功能介绍 二、设计框图 三、实物展示 四、程序 一、功能介绍硬件:树莓派3B、LD3320语音识别模块、pi 摄像头、继电器组、小灯、火焰传感器、蜂鸣器、电 磁锁 项目框架: 采用了简单工厂模式的一个设计方式。稳定,拓展性…...

《洛阳冬冷》
——洛阳的冬天太冷,最暖不过你的眼神。 ******* 她拿了个画着几丛竹子的小团扇子一路分花拂柳地往前走,后面一水儿的侍女不敢出声,只得地默默跟着她。她一张脸本来生得就好看,这一怒起来竟然还更加的好看了。此时她走得太急&…...
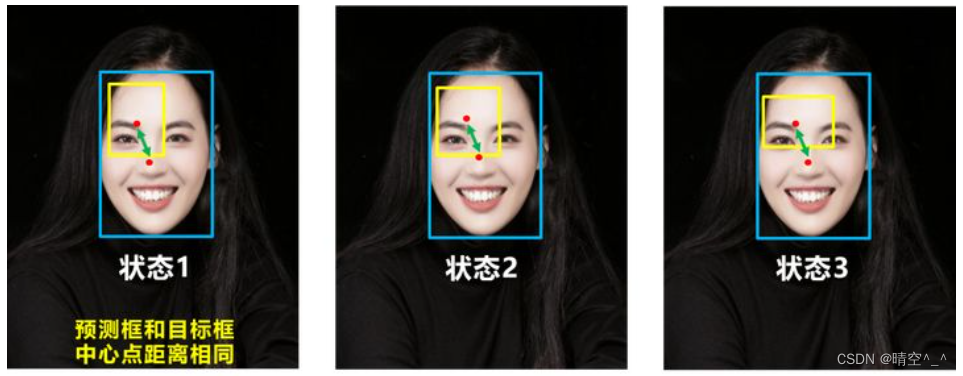
YOLOv5简介
YOLOv5 一、输入端 1. Mosaic数据增强: CutMix 数据增强:随机生成一个裁剪框Box,裁剪掉A图中的相应位置,然后用B图相应位置的ROI放到A中被裁剪的区域中形成新的样本。采用加权求和的方式计算损失,将A区域中被cut掉的…...
【面向对象语言三大特性之 “继承”】
目录 1.继承的概念及定义 1.1继承的概念 1.2 继承定义 1.2.1定义格式 1.2.2继承关系和访问限定符 1.2.3继承基类成员访问方式的变化 2.基类和派生类对象赋值转换 3.继承中的作用域 4.派生类的默认成员函数 5.继承与友元 6. 继承与静态成员 7.复杂的菱形继承及菱形虚拟…...
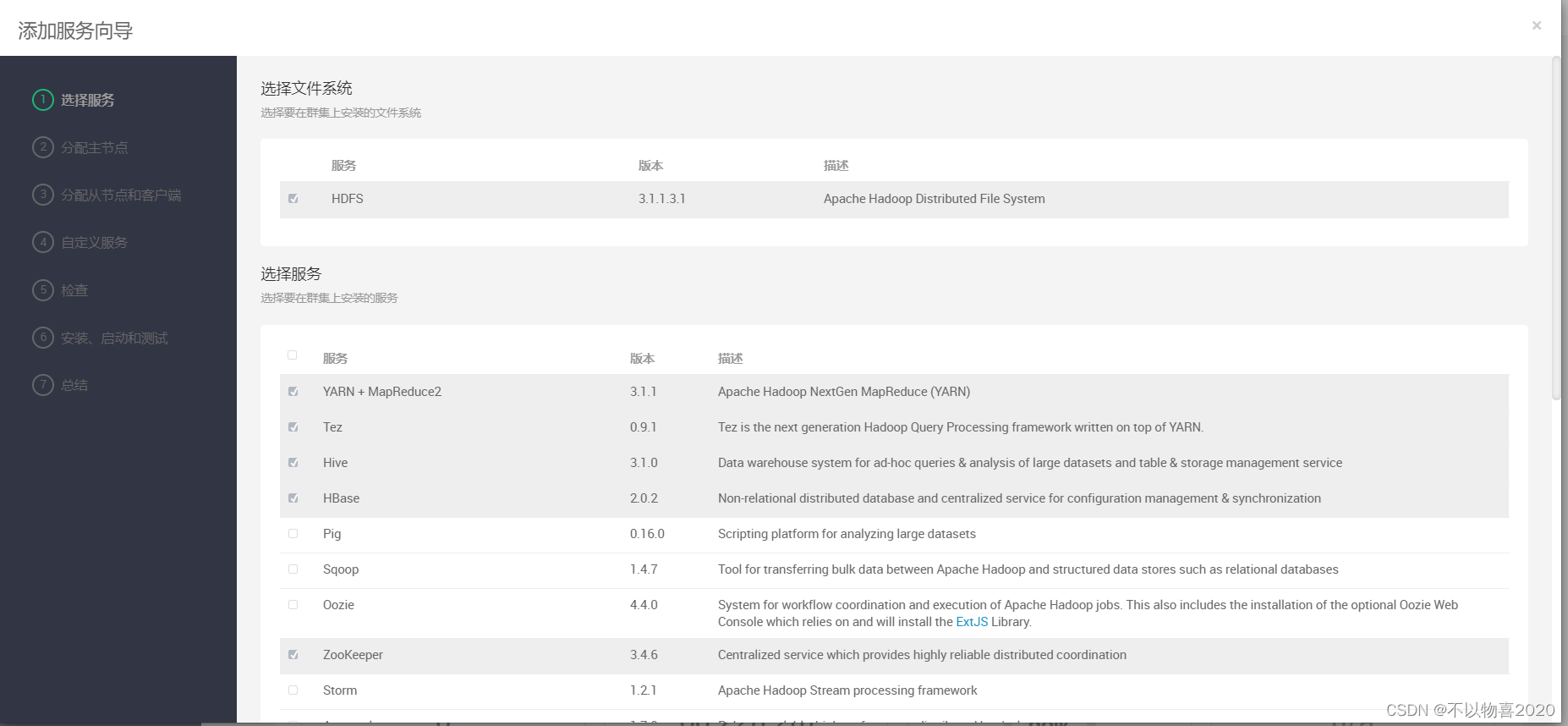
Ambari2.7.5集群搭建详细流程
0 说明 本文基于本地虚拟机从零开始搭建ambari集群 1 前置条件 1.1 本地虚拟机环境 节点角色ambari-1ambari-server ambari-agentambari-2ambari-agentambari-3ambari-agent 1.2 安装包 1.3 修改主机名并配置hosts文件 hostnamectl set-hostname ambari-1 hostnamectl se…...

房产|1月全国70城房价出炉!疫情放开后你关心的城市房价有何变化
2023年1月份,70个大中城市中新房销售价格环比上涨城市个数增加;一线城市新房销售价格环比同比转涨、二三线城市环比降势趋缓,二三线城市同比下降。 | 新房/二手房12月-1月环比上涨城市数量变化 70个大中城市中,新房环比上涨城市…...

秒验 重新定义“一键登录”
现如今,一般APP在注册登录时,仍然要经历填写用户名、密码、绑定手机号等一系列传统流程,有的人认为可以通过第三方登录避免这些流程,但仍旧要经历手机验证码的环节,而且存在验证码被拦截的风险,短信费用也很…...

ZenBuster:一款功能强大的多线程跨平台URL枚举工具
关于ZenBuster ZenBuster是一款功能强大的多线程跨平台URL枚举工具,该工具基于Python开发,同时还具备暴力破解功能。 该工具适用于安全专业人员,可以在渗透测试或CTF比赛中为广大研究人员提供帮助,并收集和目标相关的各种信息。…...

2023年美赛ICM问题E:光污染 这题很好做啊!
2023年美赛ICM问题E:光污染 这题很好做啊! 我看到DS数模的分析,看似头头是道,实则GouPi不通,我出一个,用于大家…...
)
InVEST模型 | 01 InVEST模型安装(Windows10)
除了在Python Anaconda环境中进行安装InVEST模型Python安装,平时最常使用的安装方式是通过.exe直接进行安装,本节介绍的就是直接下载安装的步骤: 打开InVEST模型下载页面 链接为:https://naturalcapitalproject.stanford.edu/…...
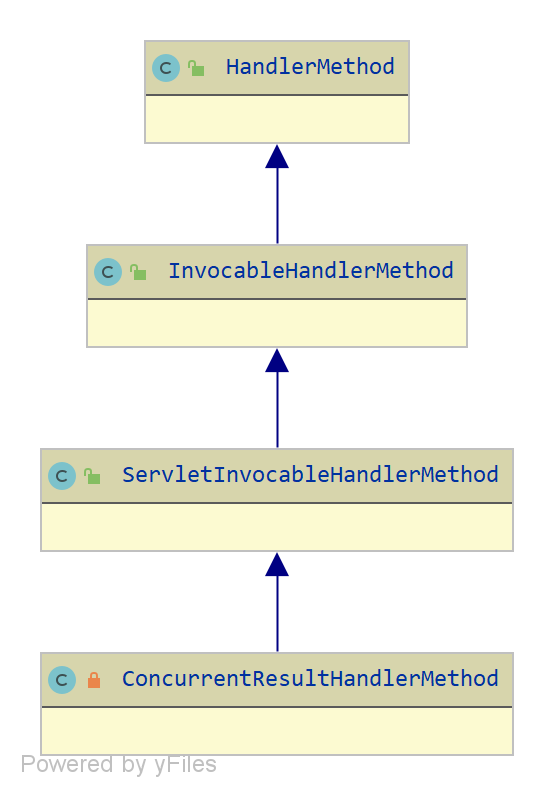
spring-web InvocableHandlerMethod 源码分析
说明 本文基于 jdk 8, spring-framework 5.2.x 编写。author JellyfishMIX - github / blog.jellyfishmix.comLICENSE GPL-2.0 类层次 HandlerMethod,处理器的方法的封装对象。HandlerMethod 只提供了处理器的方法的基本信息,不提供调用逻辑。 Invoca…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
