jenkins自定义邮件发送人姓名
jenkins发送邮件的时候发送人姓名默认的,如果要自定义发件人姓名,只需要修改如下信息即可:
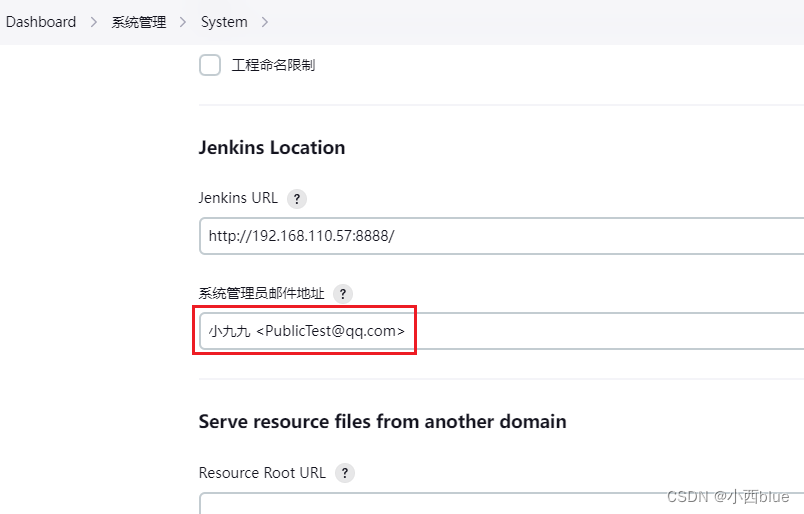
系统管理-system-Jenkins Location下的系统管理员邮件地址
格式为:自定义姓名+<邮件地址>
相关文章:

jenkins自定义邮件发送人姓名
jenkins发送邮件的时候发送人姓名默认的,如果要自定义发件人姓名,只需要修改如下信息即可: 系统管理-system-Jenkins Location下的系统管理员邮件地址 格式为:自定义姓名<邮件地址>...

SolidWorks二次开发---简单的连接solidworks
创建一个.net Framework的应用,正常4.0以上就可以了。 打开nuget包管理 在里面搜索paine 在版中选择对应的solidworks年份开头的,进行安装。 安装完之后 : 同时选中下面两个dll,把嵌入操作类型改为false 然后在按钮的单击事件中输入: Connect.Crea…...

docker 安装 active Mq
在安装完Docker的机器上,安装activeMQ。 拉取镜像: docker pull webcenter/activemq 查看镜像: docker images Docker运行ActiveMQ镜像 docker run --name activemq -d -p 8161:8161 -p 61616:61616 --privilegedtrue --restartalways …...
【Linux】TCP协议
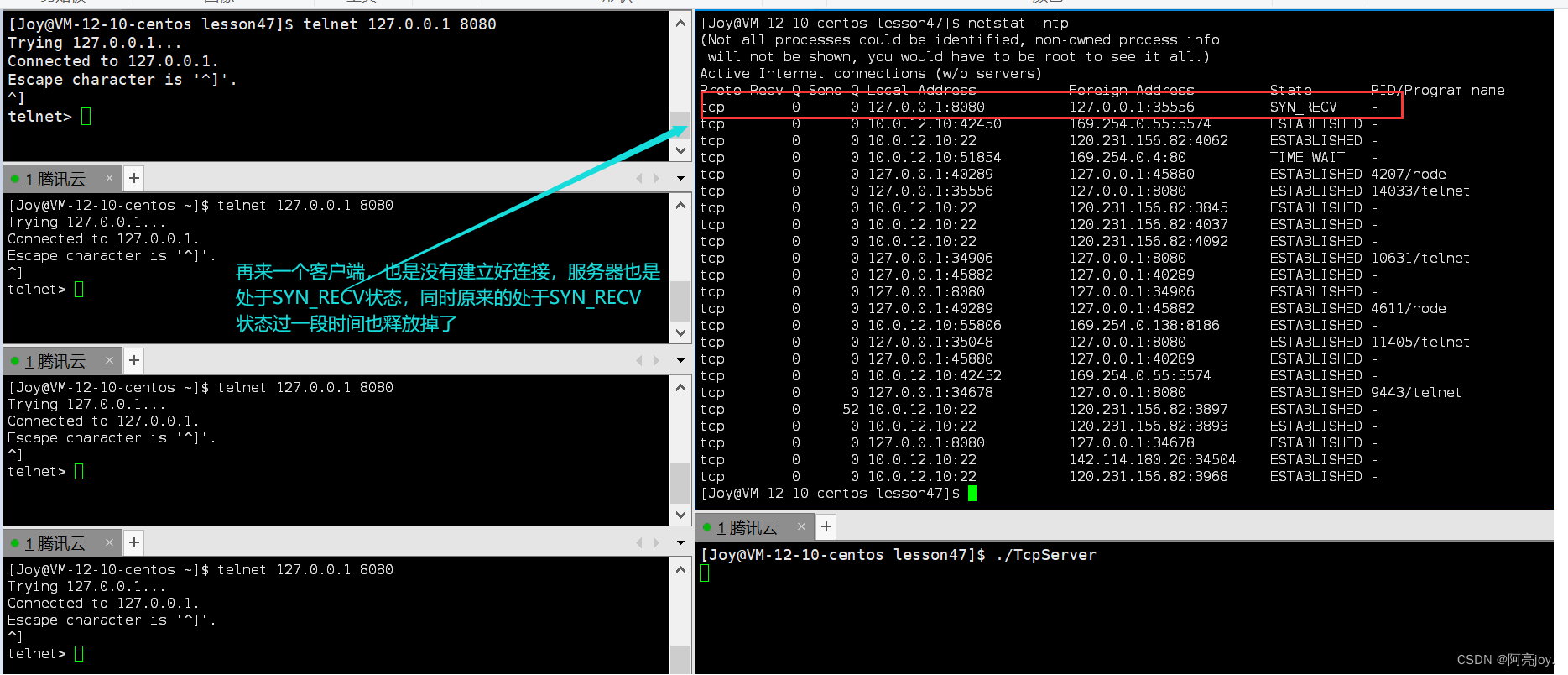
🌠 作者:阿亮joy. 🎆专栏:《学会Linux》 🎇 座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录 👉TCP协议&…...
DevOps系列文章之 自动化测试大全(单测和集成测试)
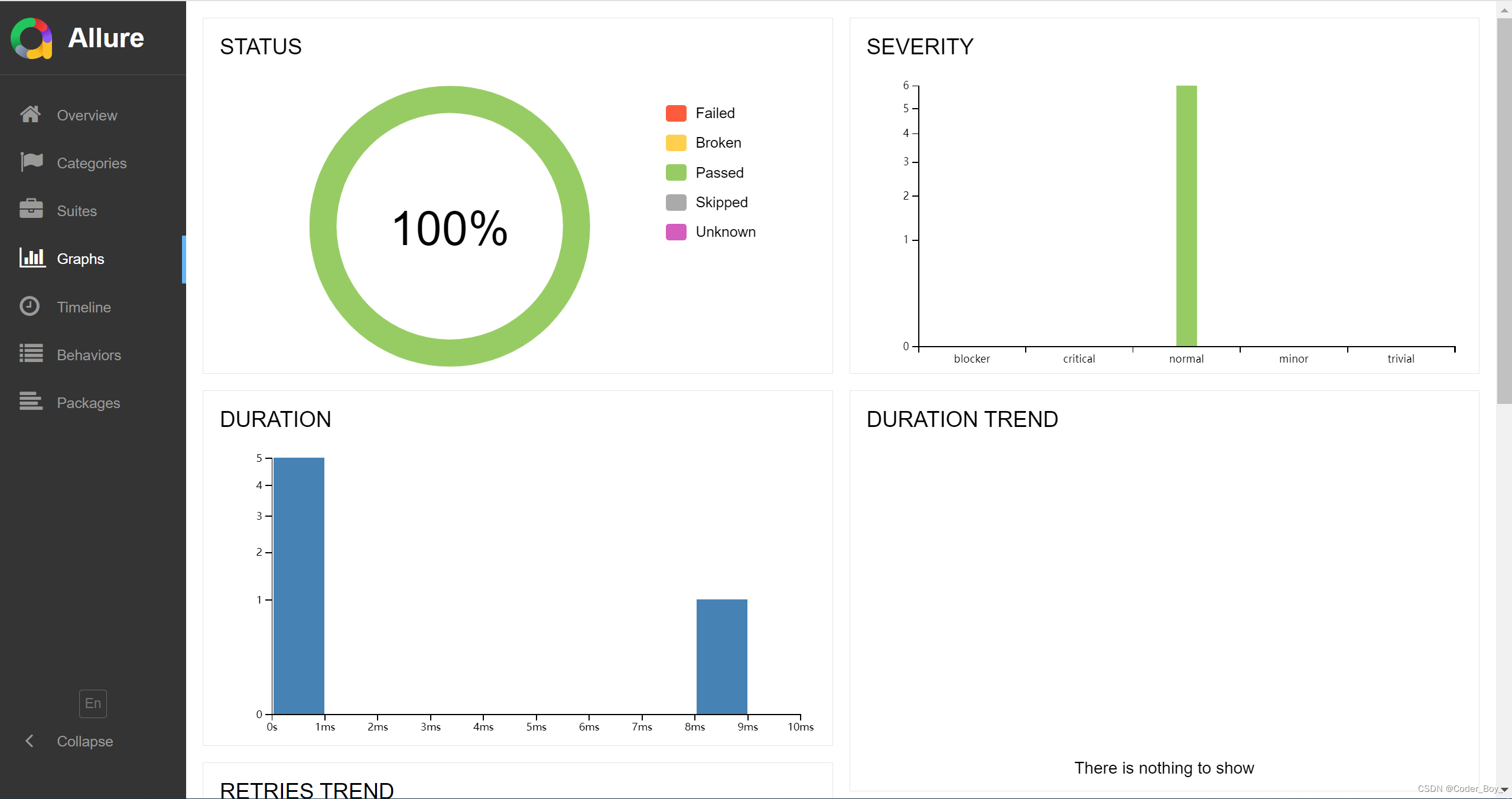
自动化测试业界主流工具 核心目标: 主要是功能测试和覆盖率测试 业界常用主流工具 GoogleTest GoogleTest是一个跨平台的(Liunx、Mac OS X、Windows 、Cygwin 、Windows CE and Symbian ) C单元测试框架,由google公司发布,为在不同平台上为编…...
Android启动速度优化
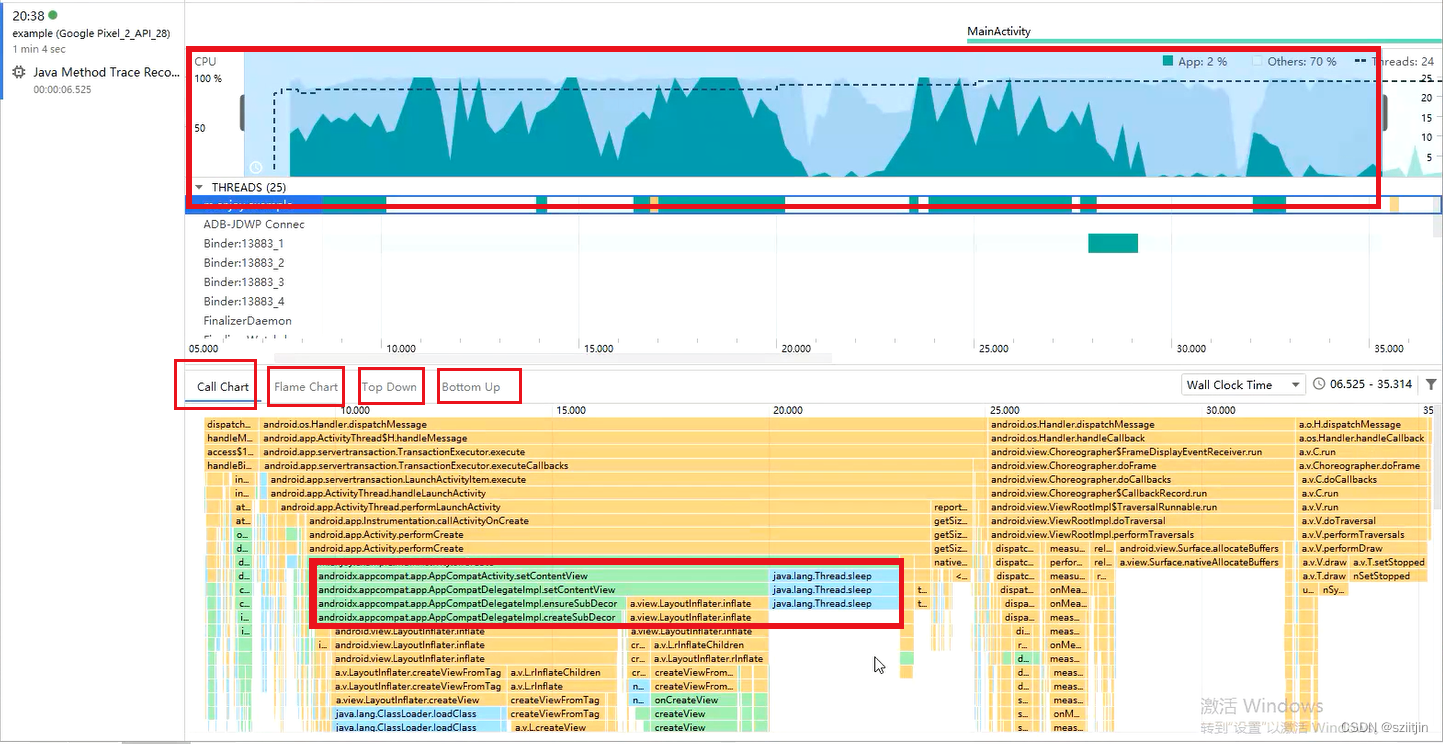
本节主要内容:了解APP启动流程、启动状态、查看启动时间、CPU Profile定位启动耗时代码、StrictMode严苛模式检测不合理写法、解决启动黑白屏问题。 一、APP启动流程 ①用户点击桌面App图标,Launcher进程采用Binder IPC向system_server进程发起startAc…...

linux 日志 系统安全日志 web日志
web日志 LINUX日志系统之WEB日志(一)_dracut.log_麻子来了的博客-CSDN博客 系统安全日志 Linux系统安全日志详解_sinolover的博客-CSDN博客 wtmp和utmp文件都是二进制文件,需使用who、w、users、last和ac来操作这两个文件。 who /var/lo…...

SpringBoot 整合 MongoDB 连接 阿里云MongoDB
注:spring-boot-starter-data-mongodb 2.7.5;jdk 1.8 阿里云MongoDB是副本集实例的 在网上查找了一番,大多数都是教连接本地mongodb或者linux上的mongodb 阿里云上有java版连接教程,但它不是SpringBoot方法配置的,是手…...

Debeizum 增量快照
在Debeizum1.6版本发布之后,成功推出了Incremental Snapshot(增量快照)的功能,同时取代了原有的实验性的Parallel Snapshot(并行快照)。在本篇博客中,我将介绍全新快照方式的原理,以…...
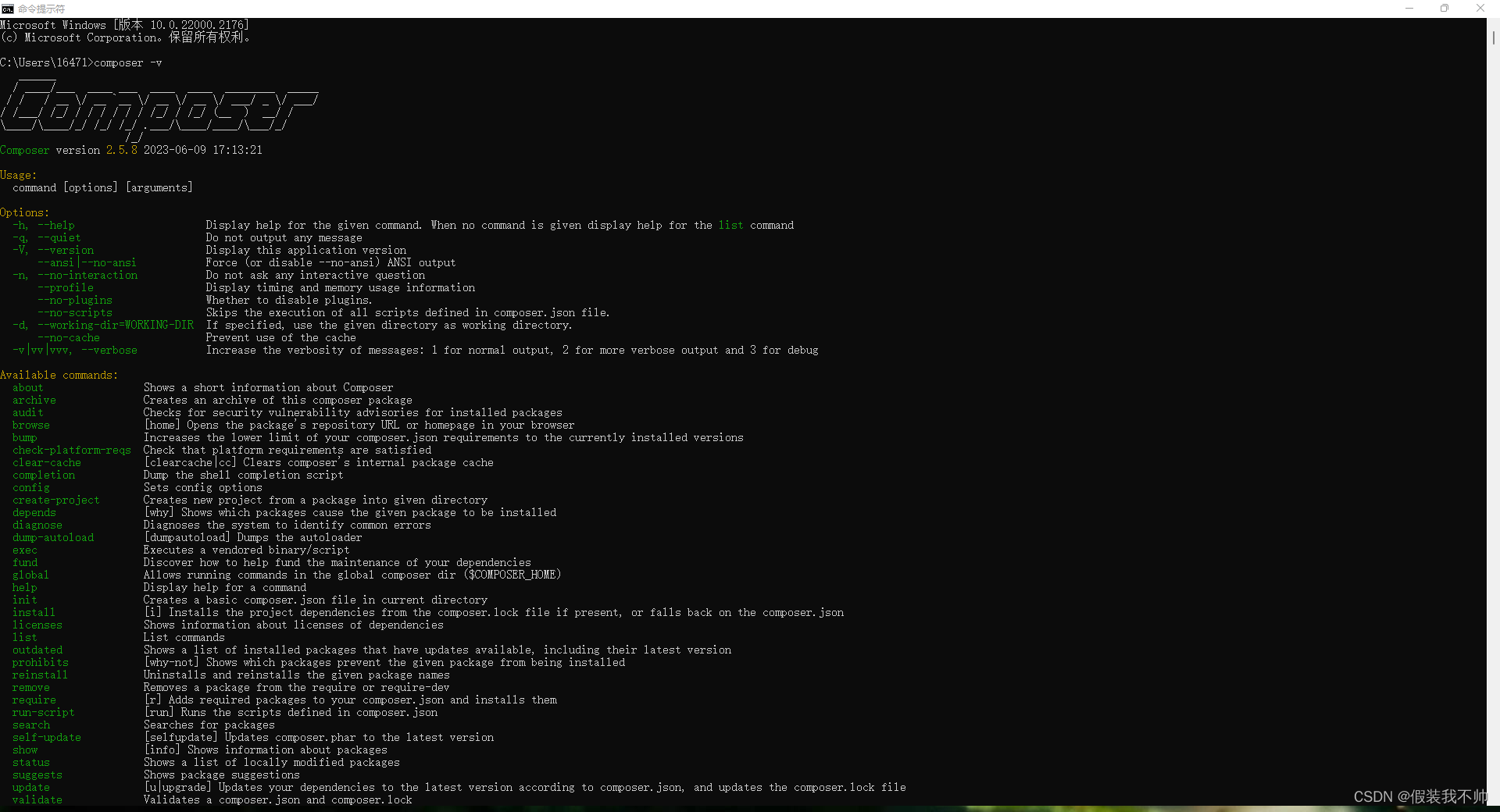
windows下安装composer
安装Php 教程 下载composer 官网 中文网站 exe下载地址 下载好exe 双击运行 找到php.ini注释一行代码 测试 composer -v说明安装成功 修改源 执行以下命令即可修改 composer config -g repo.packagist composer https://packagist.phpcomposer.com # 查看配置…...

企业游学进华秋,助力电子产业创新与发展
近日,淘IC企业游学活动,携20多位电子行业的企业家,走进了深圳华秋电子有限公司(以下简称“华秋”),进行交流学习、供需对接。华秋董事长兼CEO陈遂佰对华秋的发展历程、业务版块、产业布局等做了详尽的介绍&…...

玩转Tomcat:从安装到部署
文章目录 一、什么是 Tomcat二、Tomcat 的安装与使用2.1 下载安装2.2 目录结构2.3 启动 Tomcat 三、部署程序到 Tomcat3.1 Windows环境3.2 Linux环境 一、什么是 Tomcat 一看到 Tomcat,我们一般会想到什么?没错,就是他,童年的回忆…...

吃透《西瓜书》第四章 决策树定义与构造、ID3决策树、C4.5决策树、CART决策树
目录 一、基本概念 1.1 什么是信息熵? 1.2 决策树的定义与构造 二、决策树算法 2.1 ID3 决策树 2.2 C4.5 决策树 2.3 CART 决策树 一、基本概念 1.1 什么是信息熵? 信息熵: 熵是度量样本集合纯度最常用的一种指标,代表一个系统中蕴…...
)
复现宏景eHR存在任意文件上传漏洞(0day)
目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现 一、漏洞描述 北京宏景世纪软件股份有限公司(简称“宏景软件”)自成立以来始终专注于国有企事业单位人力与人才管理数智化(数字化、智能化)产品的研发和应用推广,是中国国有企事业单位人力与人才管理数智…...

unity连接MySQL数据库并完成增删改查
数据存储量比较大时,我就需要将数据存储在数据库中方便使用,尤其是制作管理系统时,它的用处就更大了。 在编写程序前,需要在Assets文件夹中创建plugins文件,将.dll文件导入,文件从百度网盘自取:…...

13个ChatGPT类实用AI工具汇总
在ChatGPT爆火后,各种工具如同雨后春笋一般层出不穷。以下汇总了13种ChatGPT类实用工具,可以帮助学习、教学和科研。 01 / ChatGPT for google/ 一个浏览器插件,可搭配现有的搜索引擎来使用 最大化搜索效率,对搜索体验的提升相…...
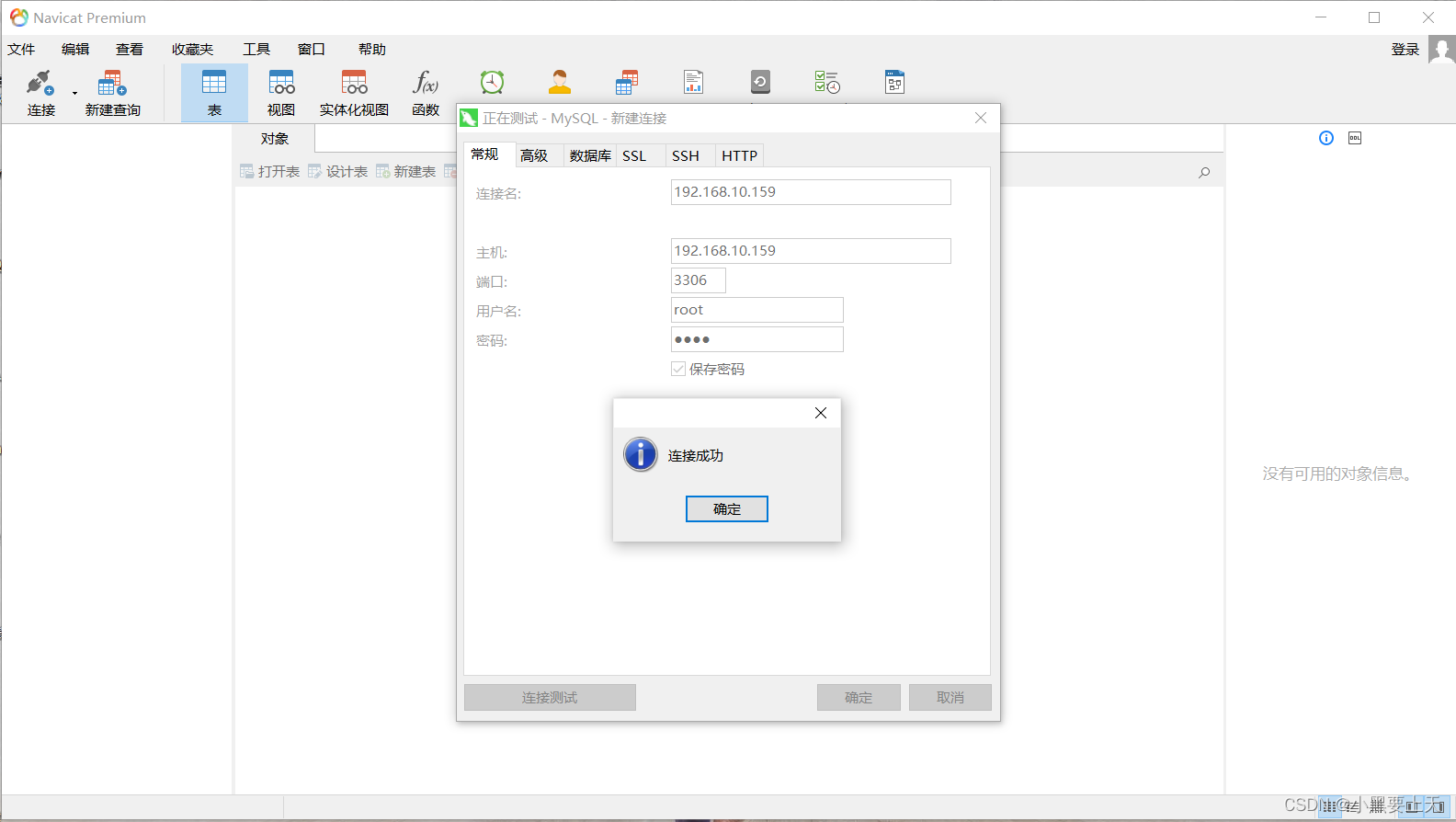
1-linux下mysql8.0.33安装
在互联网企业的日常工作/运维中,我们会经常用到mysql数据库,而linux下mysql的安装方式有三种: 1.mysql rpm安装 2.mysql二进制安装 3.mysql源码安装 今天就为大家讲讲linux下mysql8.0.33版本rpm方式的安装。 1.前提 1.1.系统版本 Cent…...
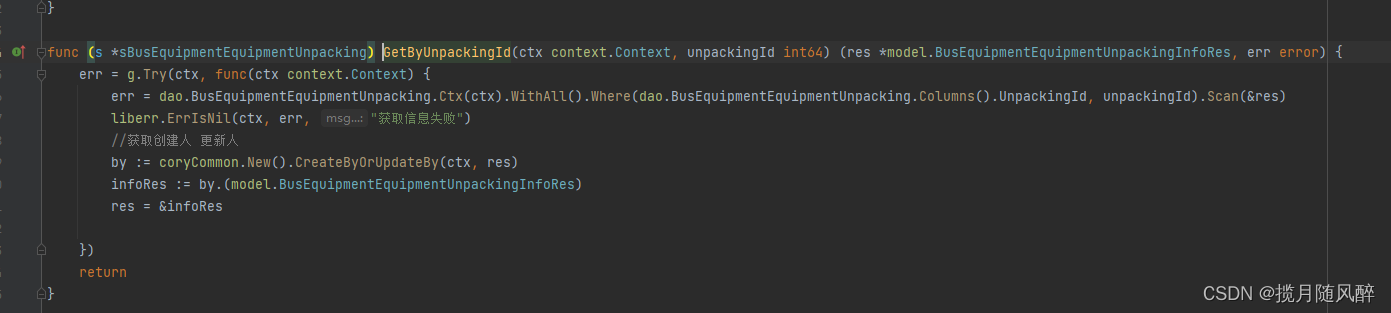
golang反射获取结构体的值和修改值
功能:根据id和反射技术封装 创建和更新人的查询 一、代码二、演示 一、代码 package coryCommonimport ("context""errors""github.com/gogf/gf/v2/container/gvar""github.com/tiger1103/gfast/v3/internal/app/system/dao&qu…...

中文大模型评估数据集——C-Eval
C-EVAL: A Multi-Level Multi-Discipline Chinese Evaluation Suite for Foundation Models https://arxiv.org/pdf/2305.08322v1.pdfhttps://github.com/SJTU-LIT/cevalhttps://cevalbenchmark.com/static/leaderboard.html Part1 前言 怎么去评估一个大语言模型呢? 在广泛…...
Unity 四元素
//-------------旋转------------ // //设置角度 (超过90或负数时,会设置-1结果是359这样的问题,可以使用下面旋转的方式) transform.rotate new Quaternion(0,0,0,0);//Quaternion四元数 transform.localEulerAngles new Vector3(0,0,0);//EulerA…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
