matlab编程实践14、15
目录
数独
"四独"游戏
解的存在和唯一性
算法
常微分方程
数独
采用蛮力试凑法来解决数独问题。(采用单选数,以及计算机科学技术中的递推回溯法)
以上的数独是图14-2的两个矩阵的和,左侧的矩阵可以由kron和magic函数建立起来,前一个函数用来求Kronecker乘积,后者生成幻方矩阵。
X = kron(eye(3), magic(3))
"四独"游戏
使用4×4网格,可能的备选项用小数标注出来。将单选数填在网格内,如果没有单选数,则采用递归回溯法来求解。(左:有单选数; 右:无单选数)
X=diag(1:4)Y=shidoku(diag(1:4)) Z=shidoku(diag(1:4)')' %可能的另一个解
解的存在和唯一性
可以用sudoku_all程序来寻找数独全部的解。
%生成数独谜题 X=kron(eye(3), magic(3)) X=sudoku_puzzle(13)数独网格的一些运算可能改变其在图形用户界面中的显示,但不能改变其基本特性。所有变化基本上都是相同的数字谜。这些等效的运算可以用matlab的数组运算表示。
%重新排列表示数字的文字 p = randperm(9), z=find(X>0). X(z)=p(X(z)) %其它运算 X', rot90(X, k) flipud(X), fliplr(X),X([4:9 1:3], :) X(:, randperm(3) 4:9)
function L = sudoku_all(X,L)
% SUDOKU_ALL Enumerate all solutions to a Sudoku puzzle.
% L = sudoku_all(X), for a 9-by-9 array X, is a list of all solutions.
% L{k} is the k-th solution.
% L{:} will print all the solutions.
% length(L) is the number of solutions. A valid puzzle must have only one.
% See also sudoku, sudoku_basic, sudoku_puzzle, sudoku_assist.if nargin < 2% Initialize the list on first entry.L = {};end% Fill in all "singletons", the cells with only one candidate.% C is the array of candidates for each cell.% N is the vector of the number of candidates for each cell.% s is the index of the first cell with the fewest candidates.[C,N] = candidates(X);while all(N>0) & any(N==1)s = find(N==1,1);X(s) = C{s};[C,N] = candidates(X);end% Add a solution to the list.if all(X(:)>0)L{end+1} = X;end% Enumerate all possible solutions.if all(N>0)Y = X;s = find(N==min(N),1);for t = [C{s}] % Iterate over the candidates.X = Y;X(s) = t; % Insert a value.L = sudoku_all(X,L); % Recursive call.endend% ------------------------------function [C,N] = candidates(X)% C = candidates(X) is a 9-by-9 cell array of vectors.% C{i,j} is the vector of allowable values for X(i,j).% N is a row vector of the number of candidates for each cell.% N(k) = Inf for cells that already have values.tri = @(k) 3*ceil(k/3-1) + (1:3);C = cell(9,9);for j = 1:9for i = 1:9if X(i,j)==0z = 1:9;z(nonzeros(X(i,:))) = 0;z(nonzeros(X(:,j))) = 0;z(nonzeros(X(tri(i),tri(j)))) = 0;C{i,j} = nonzeros(z)';endendendN = cellfun(@length,C);N(X>0) = Inf;N = N(:)';end % candidates
end % sudoku_all
算法
基本流程:
① 填入所有的单选数
②如果某个单元没有备选项,停止程序
③在某个空白的网格中填入一个试探的值
④ 递归式调用此程序
function [X,steps] = sudoku(X,steps)
% SUDOKU Solve a Sudoku puzzle using recursive backtracking.
% sudoku(X), for a 9-by-9 array X, solves the Sudoku puzzle for X.
% [X,steps] = sudoku(X) also returns the number of steps.
% See also sudoku_all, sudoku_assist, sudoku_basic, sudoku_puzzle. if nargin < 1X = sudoku_puzzle(1);endif nargin < 2steps = 0;gui_init(X);endsudoku_gui(X,steps);% Fill in all "singletons", the cells with only one candidate.% C is the array of candidates for each cell.% N is the vector of the number of candidates for each cell.% s is the index of the first cell with the fewest candidates.[C,N] = candidates(X);while all(N>0) & any(N==1)sudoku_gui(X,steps,C);s = find(N==1,1);X(s) = C{s};steps = steps + 1;sudoku_gui(X,steps,C);[C,N] = candidates(X);endsudoku_gui(X,steps,C);% Recursive backtracking.if all(N>0)Y = X;s = find(N==min(N),1);for t = [C{s}] % Iterate over the candidates.X = Y;sudoku_gui(X,steps,C);X(s) = t; % Insert a tentative value.steps = steps + 1;sudoku_gui(X,steps,C,s); % Color the tentative value.[X,steps] = sudoku(X,steps); % Recursive call.if all(X(:) > 0) % Found a solution.breakendsudoku_gui(X,steps,C,-s); % Revert color of tentative value.endendif nargin < 2gui_finish(X,steps);end% ------------------------------function [C,N] = candidates(X)% C = candidates(X) is a 9-by-9 cell array of vectors% C{i,j} is the vector of allowable values for X(i,j).% N is a row vector of the number of candidates for each cell.% N(k) = Inf for cells that already have values.tri = @(k) 3*ceil(k/3-1) + (1:3);C = cell(9,9);for j = 1:9for i = 1:9if X(i,j)==0z = 1:9;z(nonzeros(X(i,:))) = 0;z(nonzeros(X(:,j))) = 0;z(nonzeros(X(tri(i),tri(j)))) = 0;C{i,j} = nonzeros(z)';endendendN = cellfun(@length,C);N(X>0) = Inf;N = N(:)';end % candidates% ------------------------------function gui_init(X)% Initialize gui% H is the structure of handles, saved in figure userdata.dkblue = [0 0 2/3];dkgreen = [0 1/2 0];dkmagenta = [1/3 0 1/3];grey = [1/2 1/2 1/2];fsize = get(0,'defaulttextfontsize');fname = 'Lucida Sans Typewriter';clfshgset(gcf,'color','white')axis squareaxis offfor m = [2 3 5 6 8 9]line([m m]/11,[1 10]/11,'color',grey)line([1 10]/11,[m m]/11,'color',grey)endfor m = [1 4 7 10]line([m m]/11,[1 10]/11,'color',dkmagenta,'linewidth',4)line([1 10]/11,[m m]/11,'color',dkmagenta,'linewidth',4)endH.a = zeros(9,9);for j = 1:9for i = 1:9if X(i,j) > 0string = int2str(X(i,j));color = dkblue;elsestring = ' ';color = dkgreen;endH.a(i,j) = text((j+1/2)/11,(10.5-i)/11,string, ...'units','normal','fontsize',fsize+6,'fontweight','bold', ...'fontname',fname,'color',color,'horizont','center');endendstrings = {'step','slow','fast','finish'};H.b = zeros(1,4);for k = 1:4H.b(k) = uicontrol('style','toggle','string',strings{k}, ...'units','normal','position',[(k+3)*0.125,0.05,0.10,0.05], ...'background','white','value',0, ...'callback', ...'H=get(gcf,''user''); H.s=find(H.b==gco); set(gcf,''user'',H)');endset(H.b(1),'style','pushbutton')H.s = 1;H.t = title('0','fontweight','bold');set(gcf,'userdata',H)drawnowend % gui_init% ------------------------------function sudoku_gui(X,steps,C,z)H = get(gcf,'userdata');if H.s == 4if mod(steps,50) == 0set(H.t,'string',int2str(steps))drawnowendreturnelseset(H.t,'string',int2str(steps))endk = [1:H.s-1 H.s+1:4];set(H.b(k),'value',0);dkblue = [0 0 2/3];dkred = [2/3 0 0];dkgreen = [0 1/2 0];cyan = [0 2/3 2/3];fsize = get(0,'defaulttextfontsize');% Update entire array, except for initial entries.for j = 1:9for i = 1:9if ~isequal(get(H.a(i,j),'color'),dkblue) && ...~isequal(get(H.a(i,j),'color'),cyan)if X(i,j) > 0set(H.a(i,j),'string',int2str(X(i,j)),'fontsize',fsize+6, ...'color',dkgreen)elseif nargin < 3set(H.a(i,j),'string',' ')elseif length(C{i,j}) == 1set(H.a(i,j),'string',char3x3(C{i,j}),'fontsize',fsize-4, ...'color',dkred)elseset(H.a(i,j),'string',char3x3(C{i,j}),'fontsize',fsize-4, ...'color',dkgreen)endendendendif nargin == 4if z > 0set(H.a(z),'color',cyan)elseset(H.a(-z),'color',dkgreen)returnendend% Gui action = single step, brief pause, or no pauseswitch H.scase 1H.s = 0;set(gcf,'userdata',H);while H.s == 0;drawnowH = get(gcf,'userdata');endcase 2pause(0.5)case 3drawnowendif nargin == 4if z > 0set(H.a(z),'color',cyan)elseset(H.a(-z),'color',dkgreen)returnendend% ------------------------------function s = char3x3(c)% 3-by-3 character array of candidates.b = blanks(5);s = {b; b; b};for k = 1:length(c)d = c(k);p = ceil(d/3);q = 2*mod(d-1,3)+1;s{p}(q) = int2str(d);endendend % gui% ------------------------------function gui_finish(X,steps)H = get(gcf,'userdata');H.s = 2;set(H.b(1:3),'vis','off')set(gcf,'userdata',H)set(H.b(4),'string','close','value',0, ...'callback','close(gcf)')sudoku_gui(X,steps)end % gui_finishend % sudoku

备选项计算&数独题目生成:
%% Candidates备选项计算% C = candidates(X) 为向量数组构成的单元结构
% C{i,j} 为 X(i,j)构成的集合C = cell(9,9);tri = @(k) 3*ceil(k/3-1) + (1:3);for j = 1:9for i = 1:9if X(i,j)==0z = 1:9;z(nonzeros(X(i,:))) = 0;z(nonzeros(X(:,j))) = 0;z(nonzeros(X(tri(i),tri(j)))) = 0;C{i,j} = nonzeros(z)';endendendC%% First singleton and first empty. 第一个单选数,第一个空白网格% N = number of candidates in each cell.
% s = first cell with only one candidate.
% e = first cell with no candidates.N = cellfun(@length,C)s = find(X==0 & N==1,1)e = find(X==0 & N==0,1)%% Sudoku puzzles 数独题目生成help sudoku_puzzlefor p = 1:16sudoku_puzzle(p)end常微分方程
matlab提供了很多求给定常微分方程数组近似解的函数,这一常微分方程组数值解的函数包括ode23、ode45、ode113、ode23s、ode15s、ode23t、ode23tb。函数名中的数字表示所用算法的阶次,阶次和算法的复杂程度和精度有关。所有这些函数都会自动选择近似步长,来保证预先选择的精度要求。所选择的阶次越高,每一步计算量越大,但是所用的步长也越大。比如ode23算法比较二阶和三阶算法来估计计算步长,而ode45比较的是四阶和五阶算法。
s表示为stiff 刚性微分方程的求解函数。
微分方程求解程序库提供的求解函数都至少需要下面三个输入变元:
(1)F为定义微分方程组的函数
(2)tspan为描述积分区间的向量
(3) y0为初始值的向量
ode1的算法-误差较大
function [t,y] = ode1(F,tspan,y0) % ODE1 World's simplest ODE solver. % ODE1(F,[t0,tfinal],y0) uses Euler's method to solve % dy/dt = F(t,y) % with y(t0) = y0 on the interval t0 <= t <= tfinal.t0 = tspan(1); tfinal = tspan(end); h = (tfinal - t0)/200; y = y0; for t = t0:h:tfinalydot = F(t,y);y = y + h*ydot; end
用匿名函数生成微分方程:
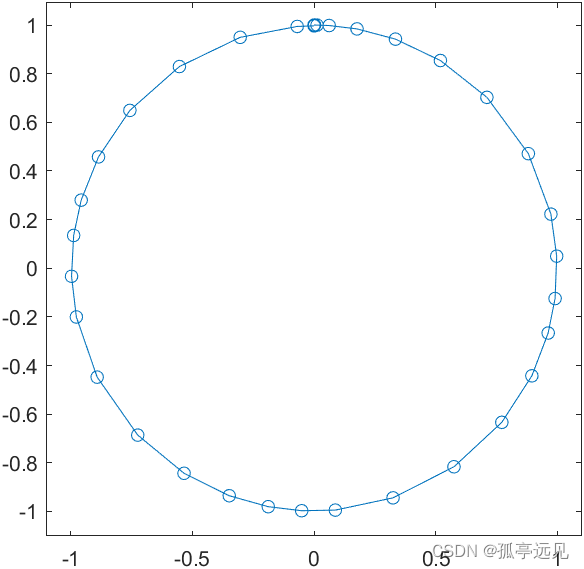
acircle = @(t,y) [y(2); -y(1)];ode23求解
%% ODE23 Automatic Plotting.figuretspan = [0 2*pi];y0 = [0; 1];ode23(acircle,tspan,y0)%% Phase Plot.figuretspan = [0 2*pi];y0 = [0; 1];[t,y] = ode23(acircle,tspan,y0)plot(y(:,1),y(:,2),'-o')axis squareaxis([-1.1 1.1 -1.1 1.1])%% ODE23 Automatic Phase Plot.opts = odeset('outputfcn',@odephas2)ode23(acircle,tspan,y0,opts)axis squareaxis([-1.1 1.1 -1.1 1.1])odeset

相关文章:

matlab编程实践14、15
目录 数独 "四独"游戏 解的存在和唯一性 算法 常微分方程 数独 采用蛮力试凑法来解决数独问题。(采用单选数,以及计算机科学技术中的递推回溯法) 以上的数独是图14-2的两个矩阵的和,左侧的矩阵可以由kron和magic函…...

C++ ——STL容器【list】模拟实现
代码仓库: list模拟实现 list源码 数据结构——双向链表 文章目录 🍇1. 节点结构体🍈2. list成员🍉3. 迭代器模板🍊4. 迭代器🍋5. 插入删除操作🍌5.1 insert & erase🍌5.2 push_…...

ubuntu 16.04 安装mujoco mujoco_py gym stable_baselines版本问题
ubuntu 16.04系统 Python 3.7.16 mujoco200 (py37mujoco) abc123:~/github/spinningup$ pip list Package Version Editable project location ----------------------------- --------- --------------------------- absl-py …...
技术)
自然语言处理(NLP)技术
自然语言处理技术是一种人工智能技术,它的目标是使计算机能够理解、分析、处理和生成自然语言(人类使用的语言)。NLP技术包括文本分类、情感分析、机器翻译、语音识别、语音合成、信息检索、信息抽取、问答系统等。NLP技术的应用非常广泛&…...
如何将ubuntu LTS升级为Pro
LTS支持周期是5年; Pro支持周期是10年。 Ubuntu Pro专业版笔记 步骤: 打开“软件和更新” 可以看到最右侧的标签是Ubuntu Pro。 在没有升级之前,如果使用下面两步: sudo apt updatesudo apt upgrade 出现如下提示ÿ…...
如何学习ARM嵌入式开发?
ARM和单片机还是有许多区别的,可以说比单片机的应用更为复杂吧,往往在单片机里只需要对一个寄存器赋值就可以的初始化,在ARM下就要调用库函数了。甚至每个引脚其功能都多了许多,相应的配置也会更为麻烦,但如果做多了AR…...

二、使用运行自己的docker python容器环境
第一篇参考: https://blog.csdn.net/weixin_42357472/article/details/131953866 运行容器同时执行命令或脚本 1)这是打开一个对外的jupyter notebook容器环境 docker run -d --name my_container -p 8090:8888 mynewpythonimage jupyter notebook --…...

mac版窗口管理 Magnet for mac中文最新
magnet mac版是一款运行在苹果电脑上的一款优秀的窗口大小控制工具,拖拽窗口到屏幕边缘可以自动半屏,全屏或者四分之一屏幕,还可以设定快捷键完成分屏。这款专业的窗口管理工具当您每次将内容从一个应用移动到另一应用时,当您需要…...
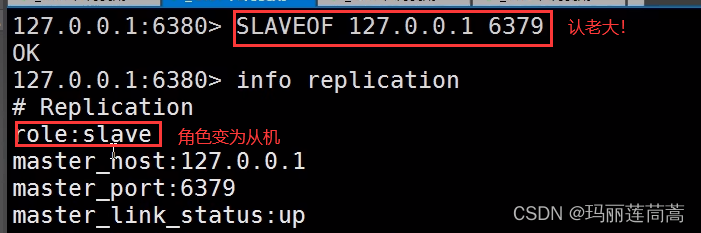
Redis(五)—— Redis进阶部分
一、Redis配置文件详解 注意这是Redis服务本身的配置文件,相当于maven的settings.xml,而不是我们在springboot去配置Redis的那个application.yml。 核心部分include 引入其他redis配置文件,相当于spring的<import>bind 设置IP…...

Go Ethereum源码学习笔记000
Go Ethereum源码学习笔记 前言时代的弄潮儿: Blockchain为什么要研究以太坊& Go-Ethereum 的原理 前言 这个专栏的内容是免费的,因为自己这边都是基于开源库和开源内容整理的学习笔记,在这个过程中进行增删改查,将自己的理解融入其中&am…...

layui 设置选中时间为当天时间最大值23:59:59、laydate设置选中时间为当天时间最大值23:59:59
既是涨知识的一天,又是干前端的一天! laydate.render({ elem: #validityPeriod, //type: datetime,//类型要一定要相匹配 type: date, // 设置日期选择模式 trigger: click, format: yyyy-MM-dd HH:mm:ss, // 设置日期的显示格式 min: startDate, max: …...

HTML+CSS+JavaScript:验证码60秒倒计时按钮
一、需求 1、打开浏览器时,按钮禁用,按钮内容为60秒倒计时 2、倒计时结束时,按钮禁用被取消 二、应用场景 1、60秒内不得重新发送验证码 2、我已阅读用户协议(5s) 三、完整代码 <!DOCTYPE html> <html l…...

互联网医院系统开发:打造便捷高效的医疗服务平台
随着互联网技术的飞速发展,互联网医院系统的出现为医疗行业带来了许多新的机遇和优势。互联网医院系统是一种基于互联网技术的医疗服务平台,旨在提供便捷、高效、个性化的医疗服务。下面将介绍互联网医院系统开发的优势。 提供便捷的医疗服务&#x…...
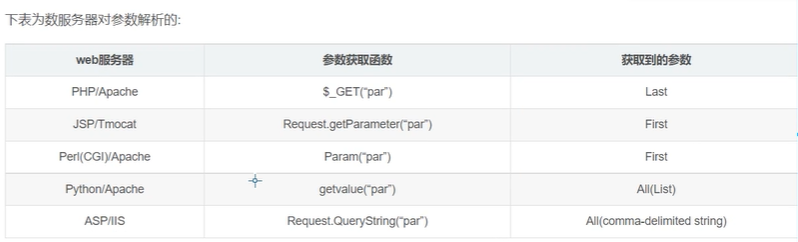
章节5:SQL注入之WAF绕过
章节5:SQL注入之WAF绕过 5.1 SQL注入之WAF绕过上 WAF拦截原理:WAF从规则库中匹配敏感字符进行拦截。 5.2 SQL注入之WAF绕过下 (原理简单了解) 关键词大小写绕过 有的WAF因为规则设计的问题,只匹配纯大写或纯小写的…...
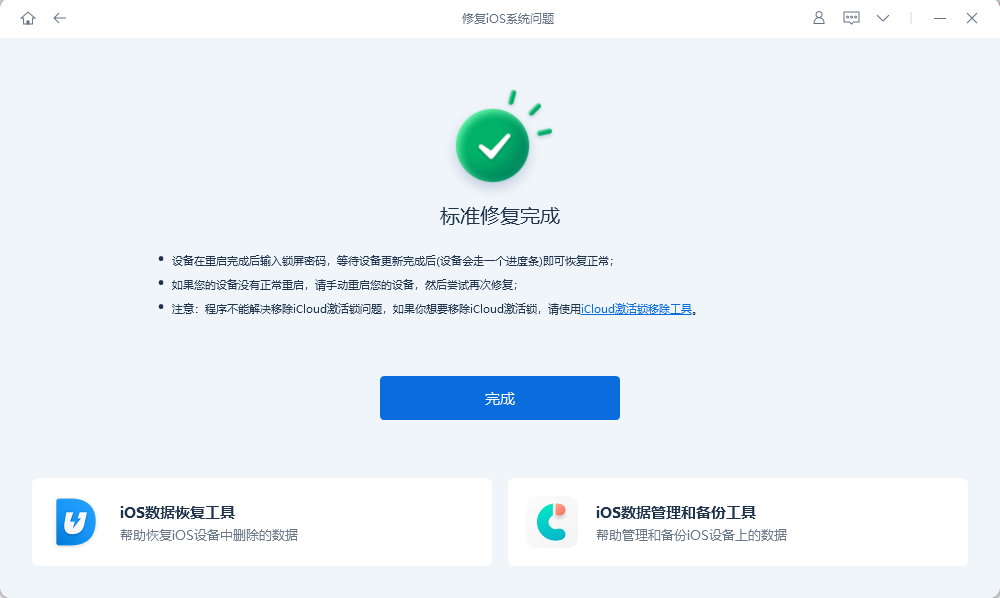
iphone卡在恢复模式怎么办?修复办法分享!
iPhone 卡在恢复屏幕问题是 iPhone 用户在软件更新或恢复期间的常见问题。如果你也遇到此问题,不要着急,接下来我们将探讨 iPhone 卡在恢复屏幕上的主要原因,以及如何轻松修复它。 iPhone卡在恢复屏幕问题上没有一个特别的原因,但…...

uniApp禁止遮罩弹窗下的页面滚动
文章目录 问题解决代码 问题 最近用uniApp开发一款软件,页面是可以滚动的长列表,自定义组件弹窗遮罩出来后,滑动屏幕,页面也跟着滚动。研究了网上的解决办法 在遮罩层的最外层的view元素中加入 touchmove.stop.prevent"moveH…...
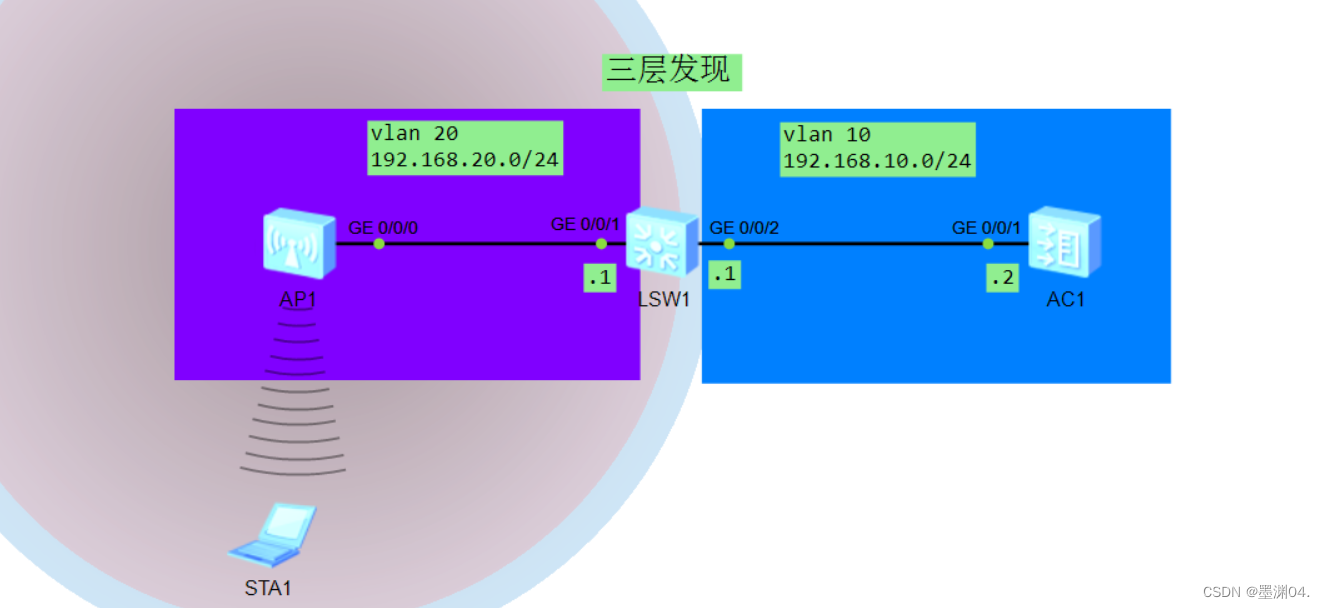
【Huawei】WLAN实验(三层发现)
拓扑图如上,AP与S1在同一VLAN,S1与AC在同一VLAN,AP采用三层发现AC,AP与客户的DHCP由S1提供。 S1配置 vlan batch 10 20 30 dhcp enable ip pool apgateway-list 192.168.20.1network 192.168.20.0 mask 255.255.255.0option 43 sub-option …...

Windows 10 安装 PostgreSQL 12.x 报错 ‘psql‘ 不是内部或外部命令 由于找不到文件libintl-9.dll等问题
目录 序言一、问题总结问题 1 psql 不是内部或外部命令,也不是可运行的程序或批处理文件。问题 2 “由于找不到文件libintl-9.dll,无法继续执行代码,重新安装程序可能会解决此问题。“1、卸载2、安装3、安装 Stack Builder (这个可…...
)
在CSDN学Golang云原生(持续交付Argo)
一,Argo安装配置 Argo是一个基于Kubernetes的容器本地工作流引擎,可以帮助用户在Kubernetes上创建、运行和维护容器化应用程序。下面是Argo安装配置的步骤: 首先确保你已经安装了kubectl和helm添加chart仓库 $ helm repo add argo https:/…...

安全运维 -- splunk 集群配置归档
0x00 背景 splunk 集群索引服务器容量满了以后,为了防止数据丢失,需要对旧数据进行归档保存。 0x01 原理 指定一台大容量服务器,创建共享文件夹,并将集群里的所有indexer指向这个归档共享目录。 0x02 实施 集群的每个indexer都…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...




