【Python机器学习】实验04(1) 多分类(基于逻辑回归)实践
文章目录
- 多分类以及机器学习实践
- 如何对多个类别进行分类
- 1.1 数据的预处理
- 1.2 训练数据的准备
- 1.3 定义假设函数，代价函数，梯度下降算法（从实验3复制过来）
- 1.4 调用梯度下降算法来学习三个分类模型的参数
- 1.5 利用模型进行预测
- 1.6 评估模型
- 1.7 试试sklearn
- 实验4(1) 请动手完成你们第一个多分类问题，祝好运！完成下面代码
- 2.1 数据读取
- 2.2 训练数据的准备
- 2.3 定义假设函数、代价函数和梯度下降算法
- 2.4 学习这四个分类模型
- 2.5 利用模型进行预测
- 2.6 计算准确率
多分类以及机器学习实践
如何对多个类别进行分类
Iris数据集是常用的分类实验数据集，由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。数据集包含150个数据样本，分为3类，每类50个数据，每个数据包含4个属性。可通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。
iris以鸢尾花的特征作为数据来源，常用在分类操作中。该数据集由3种不同类型的鸢尾花的各50个样本数据构成。其中的一个种类与另外两个种类是线性可分离的，后两个种类是非线性可分离的。
该数据集包含了4个属性：
Sepal.Length（花萼长度），单位是cm;
Sepal.Width（花萼宽度），单位是cm;
Petal.Length（花瓣长度），单位是cm;
Petal.Width（花瓣宽度），单位是cm;
种类：Iris Setosa（山鸢尾）、Iris Versicolour（杂色鸢尾），以及Iris Virginica（维吉尼亚鸢尾）。
1.1 数据的预处理
import sklearn.datasets as datasets
import pandas as pd
import numpy as np
data=datasets.load_iris()
data
{'data': array([[5.1, 3.5, 1.4, 0.2],[4.9, 3. , 1.4, 0.2],[4.7, 3.2, 1.3, 0.2],[4.6, 3.1, 1.5, 0.2],[5. , 3.6, 1.4, 0.2],[5.4, 3.9, 1.7, 0.4],[4.6, 3.4, 1.4, 0.3],[5. , 3.4, 1.5, 0.2],[4.4, 2.9, 1.4, 0.2],[4.9, 3.1, 1.5, 0.1],[5.4, 3.7, 1.5, 0.2],[4.8, 3.4, 1.6, 0.2],[4.8, 3. , 1.4, 0.1],[4.3, 3. , 1.1, 0.1],[5.8, 4. , 1.2, 0.2],[5.7, 4.4, 1.5, 0.4],[5.4, 3.9, 1.3, 0.4],[5.1, 3.5, 1.4, 0.3],[5.7, 3.8, 1.7, 0.3],[5.1, 3.8, 1.5, 0.3],[5.4, 3.4, 1.7, 0.2],[5.1, 3.7, 1.5, 0.4],[4.6, 3.6, 1. , 0.2],[5.1, 3.3, 1.7, 0.5],[4.8, 3.4, 1.9, 0.2],[5. , 3. , 1.6, 0.2],[5. , 3.4, 1.6, 0.4],[5.2, 3.5, 1.5, 0.2],[5.2, 3.4, 1.4, 0.2],[4.7, 3.2, 1.6, 0.2],[4.8, 3.1, 1.6, 0.2],[5.4, 3.4, 1.5, 0.4],[5.2, 4.1, 1.5, 0.1],[5.5, 4.2, 1.4, 0.2],[4.9, 3.1, 1.5, 0.2],[5. , 3.2, 1.2, 0.2],[5.5, 3.5, 1.3, 0.2],[4.9, 3.6, 1.4, 0.1],[4.4, 3. , 1.3, 0.2],[5.1, 3.4, 1.5, 0.2],[5. , 3.5, 1.3, 0.3],[4.5, 2.3, 1.3, 0.3],[4.4, 3.2, 1.3, 0.2],[5. , 3.5, 1.6, 0.6],[5.1, 3.8, 1.9, 0.4],[4.8, 3. , 1.4, 0.3],[5.1, 3.8, 1.6, 0.2],[4.6, 3.2, 1.4, 0.2],[5.3, 3.7, 1.5, 0.2],[5. , 3.3, 1.4, 0.2],[7. , 3.2, 4.7, 1.4],[6.4, 3.2, 4.5, 1.5],[6.9, 3.1, 4.9, 1.5],[5.5, 2.3, 4. , 1.3],[6.5, 2.8, 4.6, 1.5],[5.7, 2.8, 4.5, 1.3],[6.3, 3.3, 4.7, 1.6],[4.9, 2.4, 3.3, 1. ],[6.6, 2.9, 4.6, 1.3],[5.2, 2.7, 3.9, 1.4],[5. , 2. , 3.5, 1. ],[5.9, 3. , 4.2, 1.5],[6. , 2.2, 4. , 1. ],[6.1, 2.9, 4.7, 1.4],[5.6, 2.9, 3.6, 1.3],[6.7, 3.1, 4.4, 1.4],[5.6, 3. , 4.5, 1.5],[5.8, 2.7, 4.1, 1. ],[6.2, 2.2, 4.5, 1.5],[5.6, 2.5, 3.9, 1.1],[5.9, 3.2, 4.8, 1.8],[6.1, 2.8, 4. , 1.3],[6.3, 2.5, 4.9, 1.5],[6.1, 2.8, 4.7, 1.2],[6.4, 2.9, 4.3, 1.3],[6.6, 3. , 4.4, 1.4],[6.8, 2.8, 4.8, 1.4],[6.7, 3. , 5. , 1.7],[6. , 2.9, 4.5, 1.5],[5.7, 2.6, 3.5, 1. ],[5.5, 2.4, 3.8, 1.1],[5.5, 2.4, 3.7, 1. ],[5.8, 2.7, 3.9, 1.2],[6. , 2.7, 5.1, 1.6],[5.4, 3. , 4.5, 1.5],[6. , 3.4, 4.5, 1.6],[6.7, 3.1, 4.7, 1.5],[6.3, 2.3, 4.4, 1.3],[5.6, 3. , 4.1, 1.3],[5.5, 2.5, 4. , 1.3],[5.5, 2.6, 4.4, 1.2],[6.1, 3. , 4.6, 1.4],[5.8, 2.6, 4. , 1.2],[5. , 2.3, 3.3, 1. ],[5.6, 2.7, 4.2, 1.3],[5.7, 3. , 4.2, 1.2],[5.7, 2.9, 4.2, 1.3],[6.2, 2.9, 4.3, 1.3],[5.1, 2.5, 3. , 1.1],[5.7, 2.8, 4.1, 1.3],[6.3, 3.3, 6. , 2.5],[5.8, 2.7, 5.1, 1.9],[7.1, 3. , 5.9, 2.1],[6.3, 2.9, 5.6, 1.8],[6.5, 3. , 5.8, 2.2],[7.6, 3. , 6.6, 2.1],[4.9, 2.5, 4.5, 1.7],[7.3, 2.9, 6.3, 1.8],[6.7, 2.5, 5.8, 1.8],[7.2, 3.6, 6.1, 2.5],[6.5, 3.2, 5.1, 2. ],[6.4, 2.7, 5.3, 1.9],[6.8, 3. , 5.5, 2.1],[5.7, 2.5, 5. , 2. ],[5.8, 2.8, 5.1, 2.4],[6.4, 3.2, 5.3, 2.3],[6.5, 3. , 5.5, 1.8],[7.7, 3.8, 6.7, 2.2],[7.7, 2.6, 6.9, 2.3],[6. , 2.2, 5. , 1.5],[6.9, 3.2, 5.7, 2.3],[5.6, 2.8, 4.9, 2. ],[7.7, 2.8, 6.7, 2. ],[6.3, 2.7, 4.9, 1.8],[6.7, 3.3, 5.7, 2.1],[7.2, 3.2, 6. , 1.8],[6.2, 2.8, 4.8, 1.8],[6.1, 3. , 4.9, 1.8],[6.4, 2.8, 5.6, 2.1],[7.2, 3. , 5.8, 1.6],[7.4, 2.8, 6.1, 1.9],[7.9, 3.8, 6.4, 2. ],[6.4, 2.8, 5.6, 2.2],[6.3, 2.8, 5.1, 1.5],[6.1, 2.6, 5.6, 1.4],[7.7, 3. , 6.1, 2.3],[6.3, 3.4, 5.6, 2.4],[6.4, 3.1, 5.5, 1.8],[6. , 3. , 4.8, 1.8],[6.9, 3.1, 5.4, 2.1],[6.7, 3.1, 5.6, 2.4],[6.9, 3.1, 5.1, 2.3],[5.8, 2.7, 5.1, 1.9],[6.8, 3.2, 5.9, 2.3],[6.7, 3.3, 5.7, 2.5],[6.7, 3. , 5.2, 2.3],[6.3, 2.5, 5. , 1.9],[6.5, 3. , 5.2, 2. ],[6.2, 3.4, 5.4, 2.3],[5.9, 3. , 5.1, 1.8]]),'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]),'frame': None,'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),'DESCR': '.. _iris_dataset:\n\nIris plants dataset\n--------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 150 (50 in each of three classes)\n :Number of Attributes: 4 numeric, predictive attributes and the class\n :Attribute Information:\n - sepal length in cm\n - sepal width in cm\n - petal length in cm\n - petal width in cm\n - class:\n - Iris-Setosa\n - Iris-Versicolour\n - Iris-Virginica\n \n :Summary Statistics:\n\n ============== ==== ==== ======= ===== ====================\n Min Max Mean SD Class Correlation\n ============== ==== ==== ======= ===== ====================\n sepal length: 4.3 7.9 5.84 0.83 0.7826\n sepal width: 2.0 4.4 3.05 0.43 -0.4194\n petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)\n petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)\n ============== ==== ==== ======= ===== ====================\n\n :Missing Attribute Values: None\n :Class Distribution: 33.3% for each of 3 classes.\n :Creator: R.A. Fisher\n :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)\n :Date: July, 1988\n\nThe famous Iris database, first used by Sir R.A. Fisher. The dataset is taken\nfrom Fisher\'s paper. Note that it\'s the same as in R, but not as in the UCI\nMachine Learning Repository, which has two wrong data points.\n\nThis is perhaps the best known database to be found in the\npattern recognition literature. Fisher\'s paper is a classic in the field and\nis referenced frequently to this day. (See Duda & Hart, for example.) The\ndata set contains 3 classes of 50 instances each, where each class refers to a\ntype of iris plant. One class is linearly separable from the other 2; the\nlatter are NOT linearly separable from each other.\n\n.. topic:: References\n\n - Fisher, R.A. "The use of multiple measurements in taxonomic problems"\n Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to\n Mathematical Statistics" (John Wiley, NY, 1950).\n - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.\n (Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.\n - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System\n Structure and Classification Rule for Recognition in Partially Exposed\n Environments". IEEE Transactions on Pattern Analysis and Machine\n Intelligence, Vol. PAMI-2, No. 1, 67-71.\n - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions\n on Information Theory, May 1972, 431-433.\n - See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II\n conceptual clustering system finds 3 classes in the data.\n - Many, many more ...','feature_names': ['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)'],'filename': 'iris.csv','data_module': 'sklearn.datasets.data'}
data_x=data["data"]
data_y=data["target"]
data_x.shape,data_y.shape
((150, 4), (150,))
data_y=data_y.reshape([len(data_y),1])
data_y
array([[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2]])
#法1 ，用拼接的方法
data=np.hstack([data_x,data_y])
#法二： 用插入的方法
np.insert(data_x,data_x.shape[1],data_y,axis=1)
array([[5.1, 3.5, 1.4, ..., 2. , 2. , 2. ],[4.9, 3. , 1.4, ..., 2. , 2. , 2. ],[4.7, 3.2, 1.3, ..., 2. , 2. , 2. ],...,[6.5, 3. , 5.2, ..., 2. , 2. , 2. ],[6.2, 3.4, 5.4, ..., 2. , 2. , 2. ],[5.9, 3. , 5.1, ..., 2. , 2. , 2. ]])
data=pd.DataFrame(data,columns=["F1","F2","F3","F4","target"])
data
| F1 | F2 | F3 | F4 | target | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0.0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0.0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0.0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0.0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0.0 |
| ... | ... | ... | ... | ... | ... |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | 2.0 |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | 2.0 |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | 2.0 |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | 2.0 |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | 2.0 |
150 rows × 5 columns
data.insert(0,"ones",1)
data
| ones | F1 | F2 | F3 | F4 | target | |
|---|---|---|---|---|---|---|
| 0 | 1 | 5.1 | 3.5 | 1.4 | 0.2 | 0.0 |
| 1 | 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0.0 |
| 2 | 1 | 4.7 | 3.2 | 1.3 | 0.2 | 0.0 |
| 3 | 1 | 4.6 | 3.1 | 1.5 | 0.2 | 0.0 |
| 4 | 1 | 5.0 | 3.6 | 1.4 | 0.2 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... |
| 145 | 1 | 6.7 | 3.0 | 5.2 | 2.3 | 2.0 |
| 146 | 1 | 6.3 | 2.5 | 5.0 | 1.9 | 2.0 |
| 147 | 1 | 6.5 | 3.0 | 5.2 | 2.0 | 2.0 |
| 148 | 1 | 6.2 | 3.4 | 5.4 | 2.3 | 2.0 |
| 149 | 1 | 5.9 | 3.0 | 5.1 | 1.8 | 2.0 |
150 rows × 6 columns
data["target"]=data["target"].astype("int32")
data
| ones | F1 | F2 | F3 | F4 | target | |
|---|---|---|---|---|---|---|
| 0 | 1 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 2 | 1 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 3 | 1 | 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 4 | 1 | 5.0 | 3.6 | 1.4 | 0.2 | 0 |
| ... | ... | ... | ... | ... | ... | ... |
| 145 | 1 | 6.7 | 3.0 | 5.2 | 2.3 | 2 |
| 146 | 1 | 6.3 | 2.5 | 5.0 | 1.9 | 2 |
| 147 | 1 | 6.5 | 3.0 | 5.2 | 2.0 | 2 |
| 148 | 1 | 6.2 | 3.4 | 5.4 | 2.3 | 2 |
| 149 | 1 | 5.9 | 3.0 | 5.1 | 1.8 | 2 |
150 rows × 6 columns
1.2 训练数据的准备
data_x
array([[5.1, 3.5, 1.4, 0.2],[4.9, 3. , 1.4, 0.2],[4.7, 3.2, 1.3, 0.2],[4.6, 3.1, 1.5, 0.2],[5. , 3.6, 1.4, 0.2],[5.4, 3.9, 1.7, 0.4],[4.6, 3.4, 1.4, 0.3],[5. , 3.4, 1.5, 0.2],[4.4, 2.9, 1.4, 0.2],[4.9, 3.1, 1.5, 0.1],[5.4, 3.7, 1.5, 0.2],[4.8, 3.4, 1.6, 0.2],[4.8, 3. , 1.4, 0.1],[4.3, 3. , 1.1, 0.1],[5.8, 4. , 1.2, 0.2],[5.7, 4.4, 1.5, 0.4],[5.4, 3.9, 1.3, 0.4],[5.1, 3.5, 1.4, 0.3],[5.7, 3.8, 1.7, 0.3],[5.1, 3.8, 1.5, 0.3],[5.4, 3.4, 1.7, 0.2],[5.1, 3.7, 1.5, 0.4],[4.6, 3.6, 1. , 0.2],[5.1, 3.3, 1.7, 0.5],[4.8, 3.4, 1.9, 0.2],[5. , 3. , 1.6, 0.2],[5. , 3.4, 1.6, 0.4],[5.2, 3.5, 1.5, 0.2],[5.2, 3.4, 1.4, 0.2],[4.7, 3.2, 1.6, 0.2],[4.8, 3.1, 1.6, 0.2],[5.4, 3.4, 1.5, 0.4],[5.2, 4.1, 1.5, 0.1],[5.5, 4.2, 1.4, 0.2],[4.9, 3.1, 1.5, 0.2],[5. , 3.2, 1.2, 0.2],[5.5, 3.5, 1.3, 0.2],[4.9, 3.6, 1.4, 0.1],[4.4, 3. , 1.3, 0.2],[5.1, 3.4, 1.5, 0.2],[5. , 3.5, 1.3, 0.3],[4.5, 2.3, 1.3, 0.3],[4.4, 3.2, 1.3, 0.2],[5. , 3.5, 1.6, 0.6],[5.1, 3.8, 1.9, 0.4],[4.8, 3. , 1.4, 0.3],[5.1, 3.8, 1.6, 0.2],[4.6, 3.2, 1.4, 0.2],[5.3, 3.7, 1.5, 0.2],[5. , 3.3, 1.4, 0.2],[7. , 3.2, 4.7, 1.4],[6.4, 3.2, 4.5, 1.5],[6.9, 3.1, 4.9, 1.5],[5.5, 2.3, 4. , 1.3],[6.5, 2.8, 4.6, 1.5],[5.7, 2.8, 4.5, 1.3],[6.3, 3.3, 4.7, 1.6],[4.9, 2.4, 3.3, 1. ],[6.6, 2.9, 4.6, 1.3],[5.2, 2.7, 3.9, 1.4],[5. , 2. , 3.5, 1. ],[5.9, 3. , 4.2, 1.5],[6. , 2.2, 4. , 1. ],[6.1, 2.9, 4.7, 1.4],[5.6, 2.9, 3.6, 1.3],[6.7, 3.1, 4.4, 1.4],[5.6, 3. , 4.5, 1.5],[5.8, 2.7, 4.1, 1. ],[6.2, 2.2, 4.5, 1.5],[5.6, 2.5, 3.9, 1.1],[5.9, 3.2, 4.8, 1.8],[6.1, 2.8, 4. , 1.3],[6.3, 2.5, 4.9, 1.5],[6.1, 2.8, 4.7, 1.2],[6.4, 2.9, 4.3, 1.3],[6.6, 3. , 4.4, 1.4],[6.8, 2.8, 4.8, 1.4],[6.7, 3. , 5. , 1.7],[6. , 2.9, 4.5, 1.5],[5.7, 2.6, 3.5, 1. ],[5.5, 2.4, 3.8, 1.1],[5.5, 2.4, 3.7, 1. ],[5.8, 2.7, 3.9, 1.2],[6. , 2.7, 5.1, 1.6],[5.4, 3. , 4.5, 1.5],[6. , 3.4, 4.5, 1.6],[6.7, 3.1, 4.7, 1.5],[6.3, 2.3, 4.4, 1.3],[5.6, 3. , 4.1, 1.3],[5.5, 2.5, 4. , 1.3],[5.5, 2.6, 4.4, 1.2],[6.1, 3. , 4.6, 1.4],[5.8, 2.6, 4. , 1.2],[5. , 2.3, 3.3, 1. ],[5.6, 2.7, 4.2, 1.3],[5.7, 3. , 4.2, 1.2],[5.7, 2.9, 4.2, 1.3],[6.2, 2.9, 4.3, 1.3],[5.1, 2.5, 3. , 1.1],[5.7, 2.8, 4.1, 1.3],[6.3, 3.3, 6. , 2.5],[5.8, 2.7, 5.1, 1.9],[7.1, 3. , 5.9, 2.1],[6.3, 2.9, 5.6, 1.8],[6.5, 3. , 5.8, 2.2],[7.6, 3. , 6.6, 2.1],[4.9, 2.5, 4.5, 1.7],[7.3, 2.9, 6.3, 1.8],[6.7, 2.5, 5.8, 1.8],[7.2, 3.6, 6.1, 2.5],[6.5, 3.2, 5.1, 2. ],[6.4, 2.7, 5.3, 1.9],[6.8, 3. , 5.5, 2.1],[5.7, 2.5, 5. , 2. ],[5.8, 2.8, 5.1, 2.4],[6.4, 3.2, 5.3, 2.3],[6.5, 3. , 5.5, 1.8],[7.7, 3.8, 6.7, 2.2],[7.7, 2.6, 6.9, 2.3],[6. , 2.2, 5. , 1.5],[6.9, 3.2, 5.7, 2.3],[5.6, 2.8, 4.9, 2. ],[7.7, 2.8, 6.7, 2. ],[6.3, 2.7, 4.9, 1.8],[6.7, 3.3, 5.7, 2.1],[7.2, 3.2, 6. , 1.8],[6.2, 2.8, 4.8, 1.8],[6.1, 3. , 4.9, 1.8],[6.4, 2.8, 5.6, 2.1],[7.2, 3. , 5.8, 1.6],[7.4, 2.8, 6.1, 1.9],[7.9, 3.8, 6.4, 2. ],[6.4, 2.8, 5.6, 2.2],[6.3, 2.8, 5.1, 1.5],[6.1, 2.6, 5.6, 1.4],[7.7, 3. , 6.1, 2.3],[6.3, 3.4, 5.6, 2.4],[6.4, 3.1, 5.5, 1.8],[6. , 3. , 4.8, 1.8],[6.9, 3.1, 5.4, 2.1],[6.7, 3.1, 5.6, 2.4],[6.9, 3.1, 5.1, 2.3],[5.8, 2.7, 5.1, 1.9],[6.8, 3.2, 5.9, 2.3],[6.7, 3.3, 5.7, 2.5],[6.7, 3. , 5.2, 2.3],[6.3, 2.5, 5. , 1.9],[6.5, 3. , 5.2, 2. ],[6.2, 3.4, 5.4, 2.3],[5.9, 3. , 5.1, 1.8]])
data_x=np.insert(data_x,0,1,axis=1)
data_x.shape,data_y.shape
((150, 5), (150, 1))
#训练数据的特征和标签
data_x,data_y
(array([[1. , 5.1, 3.5, 1.4, 0.2],[1. , 4.9, 3. , 1.4, 0.2],[1. , 4.7, 3.2, 1.3, 0.2],[1. , 4.6, 3.1, 1.5, 0.2],[1. , 5. , 3.6, 1.4, 0.2],[1. , 5.4, 3.9, 1.7, 0.4],[1. , 4.6, 3.4, 1.4, 0.3],[1. , 5. , 3.4, 1.5, 0.2],[1. , 4.4, 2.9, 1.4, 0.2],[1. , 4.9, 3.1, 1.5, 0.1],[1. , 5.4, 3.7, 1.5, 0.2],[1. , 4.8, 3.4, 1.6, 0.2],[1. , 4.8, 3. , 1.4, 0.1],[1. , 4.3, 3. , 1.1, 0.1],[1. , 5.8, 4. , 1.2, 0.2],[1. , 5.7, 4.4, 1.5, 0.4],[1. , 5.4, 3.9, 1.3, 0.4],[1. , 5.1, 3.5, 1.4, 0.3],[1. , 5.7, 3.8, 1.7, 0.3],[1. , 5.1, 3.8, 1.5, 0.3],[1. , 5.4, 3.4, 1.7, 0.2],[1. , 5.1, 3.7, 1.5, 0.4],[1. , 4.6, 3.6, 1. , 0.2],[1. , 5.1, 3.3, 1.7, 0.5],[1. , 4.8, 3.4, 1.9, 0.2],[1. , 5. , 3. , 1.6, 0.2],[1. , 5. , 3.4, 1.6, 0.4],[1. , 5.2, 3.5, 1.5, 0.2],[1. , 5.2, 3.4, 1.4, 0.2],[1. , 4.7, 3.2, 1.6, 0.2],[1. , 4.8, 3.1, 1.6, 0.2],[1. , 5.4, 3.4, 1.5, 0.4],[1. , 5.2, 4.1, 1.5, 0.1],[1. , 5.5, 4.2, 1.4, 0.2],[1. , 4.9, 3.1, 1.5, 0.2],[1. , 5. , 3.2, 1.2, 0.2],[1. , 5.5, 3.5, 1.3, 0.2],[1. , 4.9, 3.6, 1.4, 0.1],[1. , 4.4, 3. , 1.3, 0.2],[1. , 5.1, 3.4, 1.5, 0.2],[1. , 5. , 3.5, 1.3, 0.3],[1. , 4.5, 2.3, 1.3, 0.3],[1. , 4.4, 3.2, 1.3, 0.2],[1. , 5. , 3.5, 1.6, 0.6],[1. , 5.1, 3.8, 1.9, 0.4],[1. , 4.8, 3. , 1.4, 0.3],[1. , 5.1, 3.8, 1.6, 0.2],[1. , 4.6, 3.2, 1.4, 0.2],[1. , 5.3, 3.7, 1.5, 0.2],[1. , 5. , 3.3, 1.4, 0.2],[1. , 7. , 3.2, 4.7, 1.4],[1. , 6.4, 3.2, 4.5, 1.5],[1. , 6.9, 3.1, 4.9, 1.5],[1. , 5.5, 2.3, 4. , 1.3],[1. , 6.5, 2.8, 4.6, 1.5],[1. , 5.7, 2.8, 4.5, 1.3],[1. , 6.3, 3.3, 4.7, 1.6],[1. , 4.9, 2.4, 3.3, 1. ],[1. , 6.6, 2.9, 4.6, 1.3],[1. , 5.2, 2.7, 3.9, 1.4],[1. , 5. , 2. , 3.5, 1. ],[1. , 5.9, 3. , 4.2, 1.5],[1. , 6. , 2.2, 4. , 1. ],[1. , 6.1, 2.9, 4.7, 1.4],[1. , 5.6, 2.9, 3.6, 1.3],[1. , 6.7, 3.1, 4.4, 1.4],[1. , 5.6, 3. , 4.5, 1.5],[1. , 5.8, 2.7, 4.1, 1. ],[1. , 6.2, 2.2, 4.5, 1.5],[1. , 5.6, 2.5, 3.9, 1.1],[1. , 5.9, 3.2, 4.8, 1.8],[1. , 6.1, 2.8, 4. , 1.3],[1. , 6.3, 2.5, 4.9, 1.5],[1. , 6.1, 2.8, 4.7, 1.2],[1. , 6.4, 2.9, 4.3, 1.3],[1. , 6.6, 3. , 4.4, 1.4],[1. , 6.8, 2.8, 4.8, 1.4],[1. , 6.7, 3. , 5. , 1.7],[1. , 6. , 2.9, 4.5, 1.5],[1. , 5.7, 2.6, 3.5, 1. ],[1. , 5.5, 2.4, 3.8, 1.1],[1. , 5.5, 2.4, 3.7, 1. ],[1. , 5.8, 2.7, 3.9, 1.2],[1. , 6. , 2.7, 5.1, 1.6],[1. , 5.4, 3. , 4.5, 1.5],[1. , 6. , 3.4, 4.5, 1.6],[1. , 6.7, 3.1, 4.7, 1.5],[1. , 6.3, 2.3, 4.4, 1.3],[1. , 5.6, 3. , 4.1, 1.3],[1. , 5.5, 2.5, 4. , 1.3],[1. , 5.5, 2.6, 4.4, 1.2],[1. , 6.1, 3. , 4.6, 1.4],[1. , 5.8, 2.6, 4. , 1.2],[1. , 5. , 2.3, 3.3, 1. ],[1. , 5.6, 2.7, 4.2, 1.3],[1. , 5.7, 3. , 4.2, 1.2],[1. , 5.7, 2.9, 4.2, 1.3],[1. , 6.2, 2.9, 4.3, 1.3],[1. , 5.1, 2.5, 3. , 1.1],[1. , 5.7, 2.8, 4.1, 1.3],[1. , 6.3, 3.3, 6. , 2.5],[1. , 5.8, 2.7, 5.1, 1.9],[1. , 7.1, 3. , 5.9, 2.1],[1. , 6.3, 2.9, 5.6, 1.8],[1. , 6.5, 3. , 5.8, 2.2],[1. , 7.6, 3. , 6.6, 2.1],[1. , 4.9, 2.5, 4.5, 1.7],[1. , 7.3, 2.9, 6.3, 1.8],[1. , 6.7, 2.5, 5.8, 1.8],[1. , 7.2, 3.6, 6.1, 2.5],[1. , 6.5, 3.2, 5.1, 2. ],[1. , 6.4, 2.7, 5.3, 1.9],[1. , 6.8, 3. , 5.5, 2.1],[1. , 5.7, 2.5, 5. , 2. ],[1. , 5.8, 2.8, 5.1, 2.4],[1. , 6.4, 3.2, 5.3, 2.3],[1. , 6.5, 3. , 5.5, 1.8],[1. , 7.7, 3.8, 6.7, 2.2],[1. , 7.7, 2.6, 6.9, 2.3],[1. , 6. , 2.2, 5. , 1.5],[1. , 6.9, 3.2, 5.7, 2.3],[1. , 5.6, 2.8, 4.9, 2. ],[1. , 7.7, 2.8, 6.7, 2. ],[1. , 6.3, 2.7, 4.9, 1.8],[1. , 6.7, 3.3, 5.7, 2.1],[1. , 7.2, 3.2, 6. , 1.8],[1. , 6.2, 2.8, 4.8, 1.8],[1. , 6.1, 3. , 4.9, 1.8],[1. , 6.4, 2.8, 5.6, 2.1],[1. , 7.2, 3. , 5.8, 1.6],[1. , 7.4, 2.8, 6.1, 1.9],[1. , 7.9, 3.8, 6.4, 2. ],[1. , 6.4, 2.8, 5.6, 2.2],[1. , 6.3, 2.8, 5.1, 1.5],[1. , 6.1, 2.6, 5.6, 1.4],[1. , 7.7, 3. , 6.1, 2.3],[1. , 6.3, 3.4, 5.6, 2.4],[1. , 6.4, 3.1, 5.5, 1.8],[1. , 6. , 3. , 4.8, 1.8],[1. , 6.9, 3.1, 5.4, 2.1],[1. , 6.7, 3.1, 5.6, 2.4],[1. , 6.9, 3.1, 5.1, 2.3],[1. , 5.8, 2.7, 5.1, 1.9],[1. , 6.8, 3.2, 5.9, 2.3],[1. , 6.7, 3.3, 5.7, 2.5],[1. , 6.7, 3. , 5.2, 2.3],[1. , 6.3, 2.5, 5. , 1.9],[1. , 6.5, 3. , 5.2, 2. ],[1. , 6.2, 3.4, 5.4, 2.3],[1. , 5.9, 3. , 5.1, 1.8]]),array([[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2]]))
由于有三个类别，那么在训练时三类数据要分开
data1=data.copy()
data1
| ones | F1 | F2 | F3 | F4 | target | |
|---|---|---|---|---|---|---|
| 0 | 1 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 2 | 1 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 3 | 1 | 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 4 | 1 | 5.0 | 3.6 | 1.4 | 0.2 | 0 |
| ... | ... | ... | ... | ... | ... | ... |
| 145 | 1 | 6.7 | 3.0 | 5.2 | 2.3 | 2 |
| 146 | 1 | 6.3 | 2.5 | 5.0 | 1.9 | 2 |
| 147 | 1 | 6.5 | 3.0 | 5.2 | 2.0 | 2 |
| 148 | 1 | 6.2 | 3.4 | 5.4 | 2.3 | 2 |
| 149 | 1 | 5.9 | 3.0 | 5.1 | 1.8 | 2 |
150 rows × 6 columns
data
data1.loc[data["target"]!=0,"target"]=0
data1.loc[data["target"]==0,"target"]=1
data1
| ones | F1 | F2 | F3 | F4 | target | |
|---|---|---|---|---|---|---|
| 0 | 1 | 5.1 | 3.5 | 1.4 | 0.2 | 1 |
| 1 | 1 | 4.9 | 3.0 | 1.4 | 0.2 | 1 |
| 2 | 1 | 4.7 | 3.2 | 1.3 | 0.2 | 1 |
| 3 | 1 | 4.6 | 3.1 | 1.5 | 0.2 | 1 |
| 4 | 1 | 5.0 | 3.6 | 1.4 | 0.2 | 1 |
| ... | ... | ... | ... | ... | ... | ... |
| 145 | 1 | 6.7 | 3.0 | 5.2 | 2.3 | 0 |
| 146 | 1 | 6.3 | 2.5 | 5.0 | 1.9 | 0 |
| 147 | 1 | 6.5 | 3.0 | 5.2 | 2.0 | 0 |
| 148 | 1 | 6.2 | 3.4 | 5.4 | 2.3 | 0 |
| 149 | 1 | 5.9 | 3.0 | 5.1 | 1.8 | 0 |
150 rows × 6 columns
data1_x=data1.iloc[:,:data1.shape[1]-1].values
data1_y=data1.iloc[:,data1.shape[1]-1].values
data1_x.shape,data1_y.shape
((150, 5), (150,))
#针对第二类，即第二个分类器的数据
data2=data.copy()
data2.loc[data["target"]==1,"target"]=1
data2.loc[data["target"]!=1,"target"]=0
data2["target"]==0
0 True
1 True
2 True
3 True
4 True...
145 True
146 True
147 True
148 True
149 True
Name: target, Length: 150, dtype: bool
data2.shape[1]
6
data2.iloc[50:55,:]
| ones | F1 | F2 | F3 | F4 | target | |
|---|---|---|---|---|---|---|
| 50 | 1 | 7.0 | 3.2 | 4.7 | 1.4 | 1 |
| 51 | 1 | 6.4 | 3.2 | 4.5 | 1.5 | 1 |
| 52 | 1 | 6.9 | 3.1 | 4.9 | 1.5 | 1 |
| 53 | 1 | 5.5 | 2.3 | 4.0 | 1.3 | 1 |
| 54 | 1 | 6.5 | 2.8 | 4.6 | 1.5 | 1 |
data2_x=data2.iloc[:,:data2.shape[1]-1].values
data2_y=data2.iloc[:,data2.shape[1]-1].values
#针对第三类，即第三个分类器的数据
data3=data.copy()
data3.loc[data["target"]==2,"target"]=1
data3.loc[data["target"]!=2,"target"]=0
data3
| ones | F1 | F2 | F3 | F4 | target | |
|---|---|---|---|---|---|---|
| 0 | 1 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 2 | 1 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 3 | 1 | 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 4 | 1 | 5.0 | 3.6 | 1.4 | 0.2 | 0 |
| ... | ... | ... | ... | ... | ... | ... |
| 145 | 1 | 6.7 | 3.0 | 5.2 | 2.3 | 1 |
| 146 | 1 | 6.3 | 2.5 | 5.0 | 1.9 | 1 |
| 147 | 1 | 6.5 | 3.0 | 5.2 | 2.0 | 1 |
| 148 | 1 | 6.2 | 3.4 | 5.4 | 2.3 | 1 |
| 149 | 1 | 5.9 | 3.0 | 5.1 | 1.8 | 1 |
150 rows × 6 columns
data3_x=data3.iloc[:,:data3.shape[1]-1].values
data3_y=data3.iloc[:,data3.shape[1]-1].values
1.3 定义假设函数，代价函数，梯度下降算法（从实验3复制过来）
def sigmoid(z):return 1 / (1 + np.exp(-z))
def h(X,w):z=X@wh=sigmoid(z)return h
#代价函数构造
def cost(X,w,y):#当X(m,n+1),y(m,),w(n+1,1)y_hat=sigmoid(X@w)right=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())cost=-np.sum(right)/X.shape[0]return cost
def sigmoid(z):return 1 / (1 + np.exp(-z))def h(X,w):z=X@wh=sigmoid(z)return h#代价函数构造
def cost(X,w,y):#当X(m,n+1),y(m,),w(n+1,1)y_hat=sigmoid(X@w)right=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())cost=-np.sum(right)/X.shape[0]return costdef grandient(X,y,iter_num,alpha):y=y.reshape((X.shape[0],1))w=np.zeros((X.shape[1],1))cost_lst=[] for i in range(iter_num):y_pred=h(X,w)-ytemp=np.zeros((X.shape[1],1))for j in range(X.shape[1]):right=np.multiply(y_pred.ravel(),X[:,j])gradient=1/(X.shape[0])*(np.sum(right))temp[j,0]=w[j,0]-alpha*gradientw=tempcost_lst.append(cost(X,w,y.ravel()))return w,cost_lst
1.4 调用梯度下降算法来学习三个分类模型的参数
#初始化超参数
iter_num,alpha=600000,0.001
#训练第一个模型
w1,cost_lst1=grandient(data1_x,data1_y,iter_num,alpha)
import matplotlib.pyplot as plt
plt.plot(range(iter_num),cost_lst1,"b-o")
[<matplotlib.lines.Line2D at 0x2562630b100>]
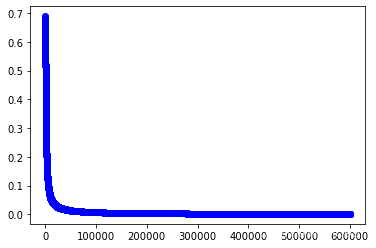
#训练第二个模型
w2,cost_lst2=grandient(data2_x,data2_y,iter_num,alpha)
import matplotlib.pyplot as plt
plt.plot(range(iter_num),cost_lst2,"b-o")
[<matplotlib.lines.Line2D at 0x25628114280>]
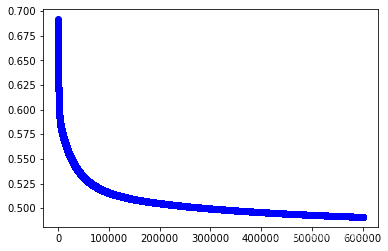
#训练第三个模型
w3,cost_lst3=grandient(data3_x,data3_y,iter_num,alpha)
w3
array([[-3.22437049],[-3.50214058],[-3.50286355],[ 5.16580317],[ 5.89898368]])
import matplotlib.pyplot as plt
plt.plot(range(iter_num),cost_lst3,"b-o")
[<matplotlib.lines.Line2D at 0x2562e0f81c0>]
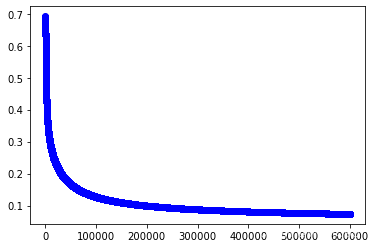
1.5 利用模型进行预测
h(data_x,w3)
array([[1.48445441e-11],[1.72343968e-10],[1.02798153e-10],[5.81975546e-10],[1.48434710e-11],[1.95971176e-11],[2.18959639e-10],[5.01346874e-11],[1.40930075e-09],[1.12830635e-10],[4.31888744e-12],[1.69308343e-10],[1.35613372e-10],[1.65858883e-10],[7.89880725e-14],[4.23224675e-13],[2.48199140e-12],[2.67766642e-11],[5.39314286e-12],[1.56935848e-11],[3.47096426e-11],[4.01827075e-11],[7.63005509e-12],[8.26864773e-10],[7.97484594e-10],[3.41189783e-10],[2.73442178e-10],[1.75314894e-11],[1.48456174e-11],[4.84204982e-10],[4.84239990e-10],[4.01914238e-11],[1.18813180e-12],[3.14985611e-13],[2.03524473e-10],[2.14461446e-11],[2.18189955e-12],[1.16799745e-11],[5.92281641e-10],[3.53217554e-11],[2.26727669e-11],[8.74004884e-09],[2.93949962e-10],[6.26783110e-10],[2.23513465e-10],[4.41246960e-10],[1.45841303e-11],[2.44584721e-10],[6.13010507e-12],[4.24539165e-11],[1.64123143e-03],[8.55503211e-03],[1.65105645e-02],[9.87814122e-02],[3.97290777e-02],[1.11076040e-01],[4.19003715e-02],[2.88426221e-03],[6.27161978e-03],[7.67020481e-02],[2.27204861e-02],[2.08212169e-02],[4.58067633e-03],[9.90450665e-02],[1.19419048e-03],[1.41462060e-03],[2.22638069e-01],[2.68940904e-03],[3.66014737e-01],[6.97791873e-03],[5.78803255e-01],[2.32071970e-03],[5.28941621e-01],[4.57649874e-02],[2.69208900e-03],[2.84603646e-03],[2.20421076e-02],[2.07507605e-01],[9.10460936e-02],[2.44824946e-04],[8.37509821e-03],[2.78543808e-03],[3.11283202e-03],[8.89831833e-01],[3.65880536e-01],[3.03993844e-02],[1.18930239e-02],[4.99150151e-02],[1.10252946e-02],[5.15923462e-02],[1.43653056e-01],[4.41610209e-02],[7.37513950e-03],[2.88447014e-03],[5.07366744e-02],[7.24617687e-03],[1.83460602e-02],[5.40874928e-03],[3.87210511e-04],[1.55791816e-02],[9.99862942e-01],[9.89637526e-01],[9.86183040e-01],[9.83705644e-01],[9.98410187e-01],[9.97834502e-01],[9.84208537e-01],[9.85434538e-01],[9.94141336e-01],[9.94561329e-01],[7.20333384e-01],[9.70431293e-01],[9.62754456e-01],[9.96609064e-01],[9.99222270e-01],[9.83684437e-01],[9.26437633e-01],[9.83486260e-01],[9.99950496e-01],[9.39002061e-01],[9.88043323e-01],[9.88637702e-01],[9.98357641e-01],[7.65848930e-01],[9.73006160e-01],[8.76969899e-01],[6.61137141e-01],[6.97324053e-01],[9.97185846e-01],[6.11033594e-01],[9.77494647e-01],[6.58573810e-01],[9.98437920e-01],[5.24529693e-01],[9.70465066e-01],[9.87624920e-01],[9.97236435e-01],[9.26432706e-01],[6.61104746e-01],[8.84442100e-01],[9.96082862e-01],[8.40940308e-01],[9.89637526e-01],[9.96974990e-01],[9.97386310e-01],[9.62040470e-01],[9.52214579e-01],[8.96902215e-01],[9.90200940e-01],[9.28785160e-01]])
#将数据输入三个模型的看看结果
multi_pred=pd.DataFrame(zip(h(data_x,w1).ravel(),h(data_x,w2).ravel(),h(data_x,w3).ravel()))
multi_pred
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.999297 | 0.108037 | 1.484454e-11 |
| 1 | 0.997061 | 0.270814 | 1.723440e-10 |
| 2 | 0.998633 | 0.164710 | 1.027982e-10 |
| 3 | 0.995774 | 0.231910 | 5.819755e-10 |
| 4 | 0.999415 | 0.085259 | 1.484347e-11 |
| ... | ... | ... | ... |
| 145 | 0.000007 | 0.127574 | 9.620405e-01 |
| 146 | 0.000006 | 0.496389 | 9.522146e-01 |
| 147 | 0.000010 | 0.234745 | 8.969022e-01 |
| 148 | 0.000006 | 0.058444 | 9.902009e-01 |
| 149 | 0.000014 | 0.284295 | 9.287852e-01 |
150 rows × 3 columns
multi_pred.values[:3]
array([[9.99297209e-01, 1.08037473e-01, 1.48445441e-11],[9.97060801e-01, 2.70813780e-01, 1.72343968e-10],[9.98632728e-01, 1.64709623e-01, 1.02798153e-10]])
#每个样本的预测值
np.argmax(multi_pred.values,axis=1)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2,2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int64)
#每个样本的真实值
data_y
array([[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[0],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2],[2]])
1.6 评估模型
np.argmax(multi_pred.values,axis=1)==data_y.ravel()
array([ True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, False, True,True, True, True, True, True, True, True, True, True,True, True, False, False, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True,True, True, True, False, True, True, True, False, True,True, True, True, True, True, True, True, True, True,True, True, True, True, True, True])
np.sum(np.argmax(multi_pred.values,axis=1)==data_y.ravel())
145
np.sum(np.argmax(multi_pred.values,axis=1)==data_y.ravel())/len(data)
0.9666666666666667
1.7 试试sklearn
from sklearn.linear_model import LogisticRegression
#建立第一个模型
clf1=LogisticRegression()
clf1.fit(data1_x,data1_y)
#建立第二个模型
clf2=LogisticRegression()
clf2.fit(data2_x,data2_y)
#建立第三个模型
clf3=LogisticRegression()
clf3.fit(data3_x,data3_y)
LogisticRegression()
y_pred1=clf1.predict(data_x)
y_pred2=clf2.predict(data_x)
y_pred3=clf3.predict(data_x)
#可视化各模型的预测结果
multi_pred=pd.DataFrame(zip(y_pred1,y_pred2,y_pred3),columns=["模型1","模糊2","模型3"])
multi_pred
| 模型1 | 模糊2 | 模型3 | |
|---|---|---|---|
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 1 | 0 | 0 |
| ... | ... | ... | ... |
| 145 | 0 | 0 | 1 |
| 146 | 0 | 1 | 1 |
| 147 | 0 | 0 | 1 |
| 148 | 0 | 0 | 1 |
| 149 | 0 | 0 | 1 |
150 rows × 3 columns
#判断预测结果
np.argmax(multi_pred.values,axis=1)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0,0, 1, 1, 1, 2, 0, 1, 1, 0, 0, 0, 2, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1,0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 2, 2, 2, 2, 2, 2, 1, 1, 1, 2,2, 2, 2, 1, 2, 2, 2, 2, 1, 1, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 1, 2,2, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2], dtype=int64)
data_y.ravel()
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
#计算准确率
np.sum(np.argmax(multi_pred.values,axis=1)==data_y.ravel())/data.shape[0]
0.7333333333333333
实验4(1) 请动手完成你们第一个多分类问题，祝好运！完成下面代码
2.1 数据读取
data_x,data_y=datasets.make_blobs(n_samples=200, n_features=6, centers=4,random_state=0)
data_x.shape,data_y.shape
((200, 6), (200,))
2.2 训练数据的准备
data=np.insert(data_x,data_x.shape[1],data_y,axis=1)
data=pd.DataFrame(data,columns=["F1","F2","F3","F4","F5","F6","target"])
data
| F1 | F2 | F3 | F4 | F5 | F6 | target | |
|---|---|---|---|---|---|---|---|
| 0 | 2.116632 | 7.972800 | -9.328969 | -8.224605 | -12.178429 | 5.498447 | 2.0 |
| 1 | 1.886449 | 4.621006 | 2.841595 | 0.431245 | -2.471350 | 2.507833 | 0.0 |
| 2 | 2.391329 | 6.464609 | -9.805900 | -7.289968 | -9.650985 | 6.388460 | 2.0 |
| 3 | -1.034776 | 6.626886 | 9.031235 | -0.812908 | 5.449855 | 0.134062 | 1.0 |
| 4 | -0.481593 | 8.191753 | 7.504717 | -1.975688 | 6.649021 | 0.636824 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 195 | 5.434893 | 7.128471 | 9.789546 | 6.061382 | 0.634133 | 5.757024 | 3.0 |
| 196 | -0.406625 | 7.586001 | 9.322750 | -1.837333 | 6.477815 | -0.992725 | 1.0 |
| 197 | 2.031462 | 7.804427 | -8.539512 | -9.824409 | -10.046935 | 6.918085 | 2.0 |
| 198 | 4.081889 | 6.127685 | 11.091126 | 4.812011 | -0.005915 | 5.342211 | 3.0 |
| 199 | 0.985744 | 7.285737 | -8.395940 | -6.586471 | -9.651765 | 6.651012 | 2.0 |
200 rows × 7 columns
data["target"]=data["target"].astype("int32")
data
| F1 | F2 | F3 | F4 | F5 | F6 | target | |
|---|---|---|---|---|---|---|---|
| 0 | 2.116632 | 7.972800 | -9.328969 | -8.224605 | -12.178429 | 5.498447 | 2 |
| 1 | 1.886449 | 4.621006 | 2.841595 | 0.431245 | -2.471350 | 2.507833 | 0 |
| 2 | 2.391329 | 6.464609 | -9.805900 | -7.289968 | -9.650985 | 6.388460 | 2 |
| 3 | -1.034776 | 6.626886 | 9.031235 | -0.812908 | 5.449855 | 0.134062 | 1 |
| 4 | -0.481593 | 8.191753 | 7.504717 | -1.975688 | 6.649021 | 0.636824 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 195 | 5.434893 | 7.128471 | 9.789546 | 6.061382 | 0.634133 | 5.757024 | 3 |
| 196 | -0.406625 | 7.586001 | 9.322750 | -1.837333 | 6.477815 | -0.992725 | 1 |
| 197 | 2.031462 | 7.804427 | -8.539512 | -9.824409 | -10.046935 | 6.918085 | 2 |
| 198 | 4.081889 | 6.127685 | 11.091126 | 4.812011 | -0.005915 | 5.342211 | 3 |
| 199 | 0.985744 | 7.285737 | -8.395940 | -6.586471 | -9.651765 | 6.651012 | 2 |
200 rows × 7 columns
data.insert(0,"ones",1)
data
| ones | F1 | F2 | F3 | F4 | F5 | F6 | target | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2.116632 | 7.972800 | -9.328969 | -8.224605 | -12.178429 | 5.498447 | 2 |
| 1 | 1 | 1.886449 | 4.621006 | 2.841595 | 0.431245 | -2.471350 | 2.507833 | 0 |
| 2 | 1 | 2.391329 | 6.464609 | -9.805900 | -7.289968 | -9.650985 | 6.388460 | 2 |
| 3 | 1 | -1.034776 | 6.626886 | 9.031235 | -0.812908 | 5.449855 | 0.134062 | 1 |
| 4 | 1 | -0.481593 | 8.191753 | 7.504717 | -1.975688 | 6.649021 | 0.636824 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 195 | 1 | 5.434893 | 7.128471 | 9.789546 | 6.061382 | 0.634133 | 5.757024 | 3 |
| 196 | 1 | -0.406625 | 7.586001 | 9.322750 | -1.837333 | 6.477815 | -0.992725 | 1 |
| 197 | 1 | 2.031462 | 7.804427 | -8.539512 | -9.824409 | -10.046935 | 6.918085 | 2 |
| 198 | 1 | 4.081889 | 6.127685 | 11.091126 | 4.812011 | -0.005915 | 5.342211 | 3 |
| 199 | 1 | 0.985744 | 7.285737 | -8.395940 | -6.586471 | -9.651765 | 6.651012 | 2 |
200 rows × 8 columns
#第一个类别的数据
data1=data.copy()
data1.loc[data["target"]==0,"target"]=1
data1.loc[data["target"]!=0,"target"]=0
data1
| ones | F1 | F2 | F3 | F4 | F5 | F6 | target | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2.116632 | 7.972800 | -9.328969 | -8.224605 | -12.178429 | 5.498447 | 0 |
| 1 | 1 | 1.886449 | 4.621006 | 2.841595 | 0.431245 | -2.471350 | 2.507833 | 1 |
| 2 | 1 | 2.391329 | 6.464609 | -9.805900 | -7.289968 | -9.650985 | 6.388460 | 0 |
| 3 | 1 | -1.034776 | 6.626886 | 9.031235 | -0.812908 | 5.449855 | 0.134062 | 0 |
| 4 | 1 | -0.481593 | 8.191753 | 7.504717 | -1.975688 | 6.649021 | 0.636824 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 195 | 1 | 5.434893 | 7.128471 | 9.789546 | 6.061382 | 0.634133 | 5.757024 | 0 |
| 196 | 1 | -0.406625 | 7.586001 | 9.322750 | -1.837333 | 6.477815 | -0.992725 | 0 |
| 197 | 1 | 2.031462 | 7.804427 | -8.539512 | -9.824409 | -10.046935 | 6.918085 | 0 |
| 198 | 1 | 4.081889 | 6.127685 | 11.091126 | 4.812011 | -0.005915 | 5.342211 | 0 |
| 199 | 1 | 0.985744 | 7.285737 | -8.395940 | -6.586471 | -9.651765 | 6.651012 | 0 |
200 rows × 8 columns
data1_x=data1.iloc[:,:data1.shape[1]-1].values
data1_y=data1.iloc[:,data1.shape[1]-1].values
data1_x.shape,data1_y.shape
((200, 7), (200,))
#第二个类别的数据
data2=data.copy()
data2.loc[data["target"]==1,"target"]=1
data2.loc[data["target"]!=1,"target"]=0
data2
| ones | F1 | F2 | F3 | F4 | F5 | F6 | target | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2.116632 | 7.972800 | -9.328969 | -8.224605 | -12.178429 | 5.498447 | 0 |
| 1 | 1 | 1.886449 | 4.621006 | 2.841595 | 0.431245 | -2.471350 | 2.507833 | 0 |
| 2 | 1 | 2.391329 | 6.464609 | -9.805900 | -7.289968 | -9.650985 | 6.388460 | 0 |
| 3 | 1 | -1.034776 | 6.626886 | 9.031235 | -0.812908 | 5.449855 | 0.134062 | 1 |
| 4 | 1 | -0.481593 | 8.191753 | 7.504717 | -1.975688 | 6.649021 | 0.636824 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 195 | 1 | 5.434893 | 7.128471 | 9.789546 | 6.061382 | 0.634133 | 5.757024 | 0 |
| 196 | 1 | -0.406625 | 7.586001 | 9.322750 | -1.837333 | 6.477815 | -0.992725 | 1 |
| 197 | 1 | 2.031462 | 7.804427 | -8.539512 | -9.824409 | -10.046935 | 6.918085 | 0 |
| 198 | 1 | 4.081889 | 6.127685 | 11.091126 | 4.812011 | -0.005915 | 5.342211 | 0 |
| 199 | 1 | 0.985744 | 7.285737 | -8.395940 | -6.586471 | -9.651765 | 6.651012 | 0 |
200 rows × 8 columns
data2_x=data2.iloc[:,:data2.shape[1]-1].values
data2_y=data2.iloc[:,data2.shape[1]-1].values
#第三个类别的数据
data3=data.copy()
data3.loc[data["target"]==2,"target"]=1
data3.loc[data["target"]!=2,"target"]=0
data3
| ones | F1 | F2 | F3 | F4 | F5 | F6 | target | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2.116632 | 7.972800 | -9.328969 | -8.224605 | -12.178429 | 5.498447 | 1 |
| 1 | 1 | 1.886449 | 4.621006 | 2.841595 | 0.431245 | -2.471350 | 2.507833 | 0 |
| 2 | 1 | 2.391329 | 6.464609 | -9.805900 | -7.289968 | -9.650985 | 6.388460 | 1 |
| 3 | 1 | -1.034776 | 6.626886 | 9.031235 | -0.812908 | 5.449855 | 0.134062 | 0 |
| 4 | 1 | -0.481593 | 8.191753 | 7.504717 | -1.975688 | 6.649021 | 0.636824 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 195 | 1 | 5.434893 | 7.128471 | 9.789546 | 6.061382 | 0.634133 | 5.757024 | 0 |
| 196 | 1 | -0.406625 | 7.586001 | 9.322750 | -1.837333 | 6.477815 | -0.992725 | 0 |
| 197 | 1 | 2.031462 | 7.804427 | -8.539512 | -9.824409 | -10.046935 | 6.918085 | 1 |
| 198 | 1 | 4.081889 | 6.127685 | 11.091126 | 4.812011 | -0.005915 | 5.342211 | 0 |
| 199 | 1 | 0.985744 | 7.285737 | -8.395940 | -6.586471 | -9.651765 | 6.651012 | 1 |
200 rows × 8 columns
data3_x=data3.iloc[:,:data3.shape[1]-1].values
data3_y=data3.iloc[:,data3.shape[1]-1].values
#第四个类别的数据
data4=data.copy()
data4.loc[data["target"]==3,"target"]=1
data4.loc[data["target"]!=3,"target"]=0
data4
| ones | F1 | F2 | F3 | F4 | F5 | F6 | target | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2.116632 | 7.972800 | -9.328969 | -8.224605 | -12.178429 | 5.498447 | 0 |
| 1 | 1 | 1.886449 | 4.621006 | 2.841595 | 0.431245 | -2.471350 | 2.507833 | 0 |
| 2 | 1 | 2.391329 | 6.464609 | -9.805900 | -7.289968 | -9.650985 | 6.388460 | 0 |
| 3 | 1 | -1.034776 | 6.626886 | 9.031235 | -0.812908 | 5.449855 | 0.134062 | 0 |
| 4 | 1 | -0.481593 | 8.191753 | 7.504717 | -1.975688 | 6.649021 | 0.636824 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 195 | 1 | 5.434893 | 7.128471 | 9.789546 | 6.061382 | 0.634133 | 5.757024 | 1 |
| 196 | 1 | -0.406625 | 7.586001 | 9.322750 | -1.837333 | 6.477815 | -0.992725 | 0 |
| 197 | 1 | 2.031462 | 7.804427 | -8.539512 | -9.824409 | -10.046935 | 6.918085 | 0 |
| 198 | 1 | 4.081889 | 6.127685 | 11.091126 | 4.812011 | -0.005915 | 5.342211 | 1 |
| 199 | 1 | 0.985744 | 7.285737 | -8.395940 | -6.586471 | -9.651765 | 6.651012 | 0 |
200 rows × 8 columns
data4_x=data4.iloc[:,:data4.shape[1]-1].values
data4_y=data4.iloc[:,data4.shape[1]-1].values
2.3 定义假设函数、代价函数和梯度下降算法
def sigmoid(z):return 1 / (1 + np.exp(-z))
def h(X,w):z=X@wh=sigmoid(z)return h
#代价函数构造
def cost(X,w,y):#当X(m,n+1),y(m,),w(n+1,1)y_hat=sigmoid(X@w)right=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())cost=-np.sum(right)/X.shape[0]return cost
def grandient(X,y,iter_num,alpha):y=y.reshape((X.shape[0],1))w=np.zeros((X.shape[1],1))cost_lst=[] for i in range(iter_num):y_pred=h(X,w)-ytemp=np.zeros((X.shape[1],1))for j in range(X.shape[1]):right=np.multiply(y_pred.ravel(),X[:,j])gradient=1/(X.shape[0])*(np.sum(right))temp[j,0]=w[j,0]-alpha*gradientw=tempcost_lst.append(cost(X,w,y.ravel()))return w,cost_lst
2.4 学习这四个分类模型
import matplotlib.pyplot as plt
#初始化超参数
iter_num,alpha=600000,0.001
#训练第1个模型
w1,cost_lst1=grandient(data1_x,data1_y,iter_num,alpha)
plt.plot(range(iter_num),cost_lst1,"b-o")
[<matplotlib.lines.Line2D at 0x25624eb08e0>]
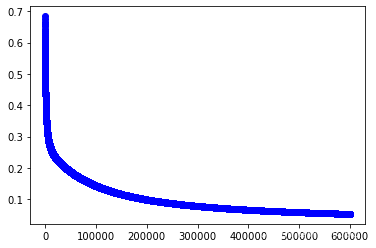
#训练第2个模型
w2,cost_lst2=grandient(data2_x,data2_y,iter_num,alpha)
plt.plot(range(iter_num),cost_lst2,"b-o")
[<matplotlib.lines.Line2D at 0x25631b87a60>]
#训练第3个模型
w3,cost_lst3=grandient(data3_x,data3_y,iter_num,alpha)
plt.plot(range(iter_num),cost_lst3,"b-o")
[<matplotlib.lines.Line2D at 0x2562bcdfac0>]
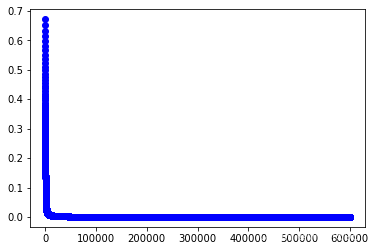
#训练第4个模型
w4,cost_lst4=grandient(data4_x,data4_y,iter_num,alpha)
plt.plot(range(iter_num),cost_lst4,"b-o")
[<matplotlib.lines.Line2D at 0x25631ff4ee0>]
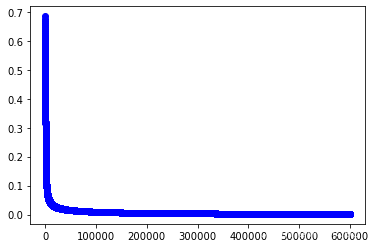
2.5 利用模型进行预测
data_x
array([[ 2.11663151e+00, 7.97280013e+00, -9.32896918e+00,-8.22460526e+00, -1.21784287e+01, 5.49844655e+00],[ 1.88644899e+00, 4.62100554e+00, 2.84159548e+00,4.31244563e-01, -2.47135027e+00, 2.50783257e+00],[ 2.39132949e+00, 6.46460915e+00, -9.80590050e+00,-7.28996786e+00, -9.65098460e+00, 6.38845956e+00],...,[ 2.03146167e+00, 7.80442707e+00, -8.53951210e+00,-9.82440872e+00, -1.00469351e+01, 6.91808489e+00],[ 4.08188906e+00, 6.12768483e+00, 1.10911262e+01,4.81201082e+00, -5.91530191e-03, 5.34221079e+00],[ 9.85744105e-01, 7.28573657e+00, -8.39593964e+00,-6.58647097e+00, -9.65176507e+00, 6.65101187e+00]])
data_x=np.insert(data_x,0,1,axis=1)
data_x.shape
(200, 7)
w3.shape
(7, 1)
multi_pred=pd.DataFrame(zip(h(data_x,w1).ravel(),h(data_x,w2).ravel(),h(data_x,w3).ravel(),h(data_x,w4).ravel()))
multi_pred
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 0.020436 | 4.556248e-15 | 9.999975e-01 | 2.601227e-27 |
| 1 | 0.820488 | 4.180906e-05 | 3.551499e-05 | 5.908691e-05 |
| 2 | 0.109309 | 7.316201e-14 | 9.999978e-01 | 7.091713e-24 |
| 3 | 0.036608 | 9.999562e-01 | 1.048562e-09 | 5.724854e-03 |
| 4 | 0.003075 | 9.999292e-01 | 2.516742e-09 | 6.423038e-05 |
| ... | ... | ... | ... | ... |
| 195 | 0.017278 | 3.221293e-06 | 3.753372e-14 | 9.999943e-01 |
| 196 | 0.003369 | 9.999966e-01 | 6.673394e-10 | 2.281428e-03 |
| 197 | 0.000606 | 1.118174e-13 | 9.999941e-01 | 1.780212e-28 |
| 198 | 0.013072 | 4.999118e-05 | 9.811154e-14 | 9.996689e-01 |
| 199 | 0.151548 | 1.329623e-13 | 9.999447e-01 | 2.571989e-24 |
200 rows × 4 columns
2.6 计算准确率
np.sum(np.argmax(multi_pred.values,axis=1)==data_y.ravel())/len(data)
1.0
相关文章：
【Python机器学习】实验04(1) 多分类(基于逻辑回归)实践
文章目录 多分类以及机器学习实践如何对多个类别进行分类1.1 数据的预处理1.2 训练数据的准备1.3 定义假设函数，代价函数，梯度下降算法（从实验3复制过来）1.4 调用梯度下降算法来学习三个分类模型的参数1.5 利用模型进行预测1.6 评…...
【ChatGLM_01】ChatGLM2-6B本地安装与部署（大语言模型）
基于本地知识库的问答 1、简介（1）ChatGLM2-6B（2）LangChain（3）基于单一文档问答的实现原理（4）大规模语言模型系列技术：以GLM-130B为例（5）新建知识库…...
扫描器搭建扩展使用教程)
谷歌Tsunami(海啸)扫描器搭建扩展使用教程
目录 介绍 下载地址 功能总结 原理 服务探测 漏洞检测 安装...
诚迈科技承办大同首届信息技术产业峰会，共话数字经济崭新未来
7月28日，“聚势而强共领信创”2023大同首届信息技术产业峰会圆满举行。本次峰会由中共大同市委、大同市人民政府主办，中国高科技产业化研究会国际交流合作中心、山西省信创协会协办，中共大同市云冈区委、大同市云冈区人民政府、诚迈科技&…...
【Python】Python使用TK实现动态爱心效果
【Python】Python使用Tk实现动态爱心效果 画布使用了缓存机制，启动时绘制足够多的帧数，运行时一帧帧地取出来展示，明显更流畅，加快了程序执行速度。将控制跳动动画的函数从正弦函数换成了贝塞尔函数，贝塞尔函数更灵活…...
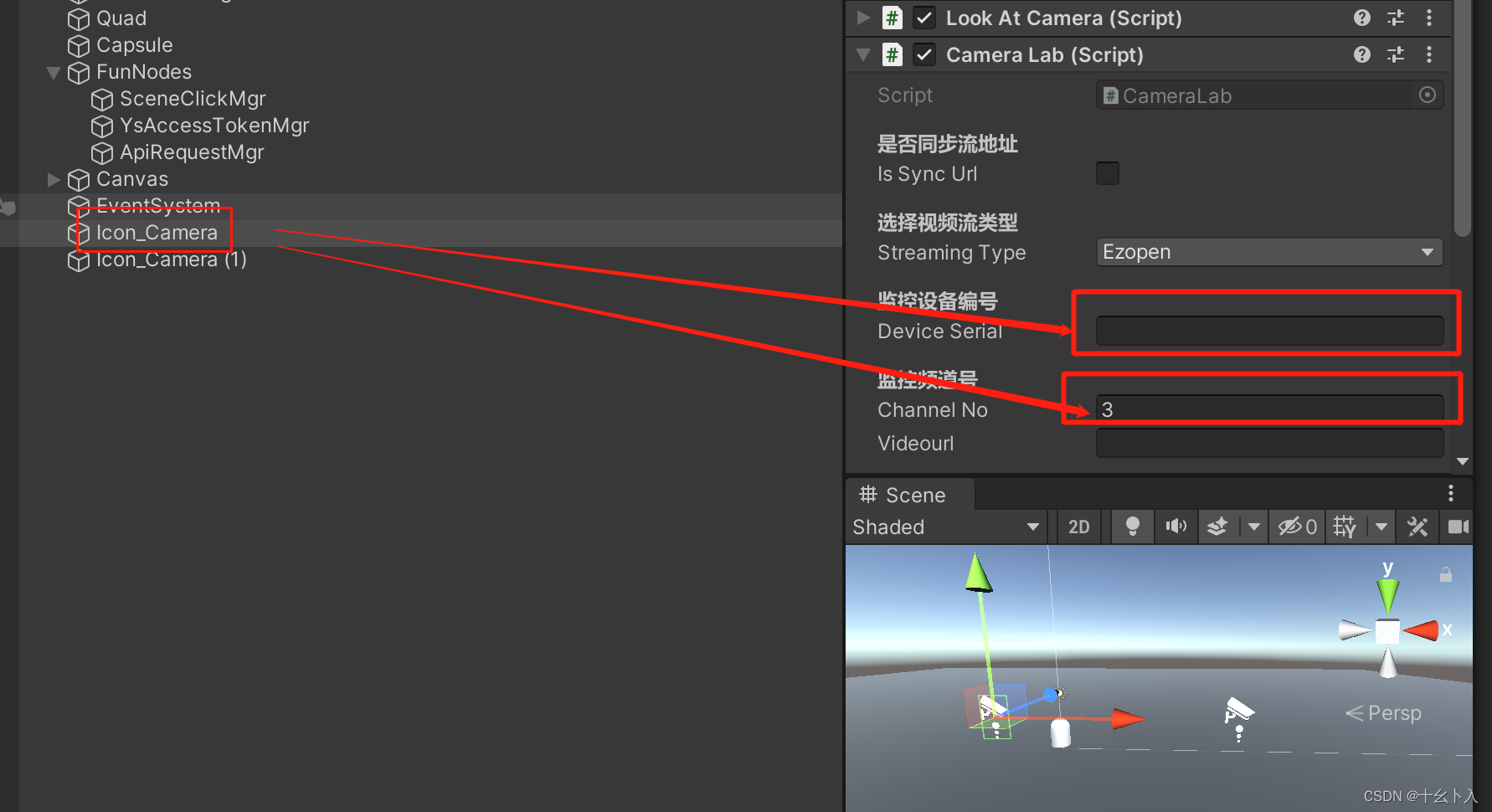
Unity3d C#快速打开萤石云监控视频流（ezopen）支持WebGL平台，替代UMP播放视频流的方案（含源码）
前言 Universal Media Player算是视频流播放功能常用的插件了，用到现在已经不知道躺了多少坑了，这个插件虽然是白嫖的，不过被甲方和领导吐槽的就是播放视频流的速度特别慢，可能需要几十秒来打开监控画面，等待的时间较…...
【Android】APP启动优化学习笔记
启动优化目的 用户体验： 应用的启动速度直接影响用户体验。用户希望应用能够快速启动并迅速响应他们的操作。如果应用启动较慢，用户可能会感到不满，并且有可能选择卸载或切换到竞争对手的应用。通过启动优化，可以提高应用的启动…...
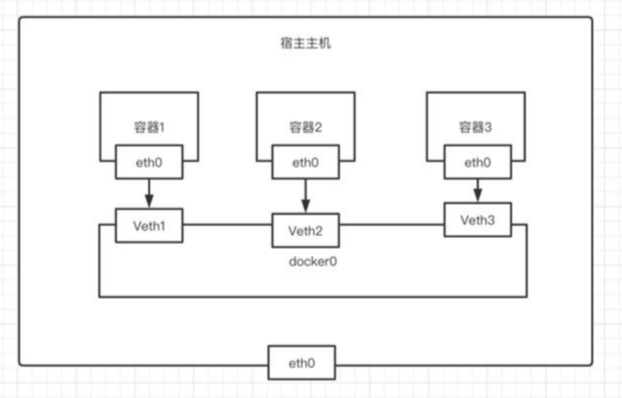
docker的使用
docker安装 https://docs.docker.com/engine/install/debian/ 设置国内镜像 创建或修改 /etc/docker/daemon.json 文件，修改为如下形式 {"registry-mirrors": ["https://registry.hub.docker.com","http://hub-mirror.c.163.com"…...
iOS使用Rust调研
编辑已恢复 我们已与您断开连接。尝试重连时会保存您所做的变更。尝试重连 标题 1 已保存 Bin Song B 要发布此内容，请选择键盘上的 ⌘Enter。 发布 关闭 Rust技术空间 … 跨平台使用调研 iOS使用Rust调研 添加表情符号 添加标题图像 添加状态 一、iOS 项…...
抖音引流推广的几个方法，抖音全自动引流脚本软件详细使用教学
大家好我是你们的小编一辞脚本，今天给大家分享新的知识，很开心可以在CSDN平台分享知识给大家,很多伙伴看不到代码我先录制一下视频 在给大家做代码，给大家分享一下抖音引流脚本的知识和视频演示 不懂的小伙伴可以认真看一下，我们…...
k8s概念-DaemonSet
回到目录 参考链接https://v1-23.docs.kubernetes.io/zh/docs/concepts/workloads/controllers/daemonset/ DaemonSet 确保全部（或者某些）节点上运行一个 Pod 的副本 当节点加入到K8S集群中，pod会被（DaemonSet）调度到…...
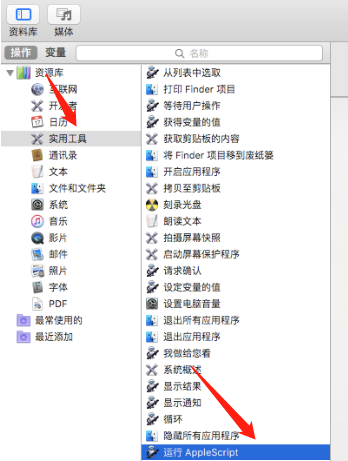
Mac 终端快捷键设置：如何给 Mac 中的 Terminal 设置 Ctrl+Alt+T 快捷键快速启动
Mac 电脑中正常是没有直接打开终端命令行的快捷键指令的，但可以通过 commandspace 打开聚焦搜索，然后输入 ter 或者 terminal 全拼打开。但习惯了 linux 的同学会觉得这个操作很别扭。于是我们希望能通过键盘按键直接打开。 操作流程如下： 1…...
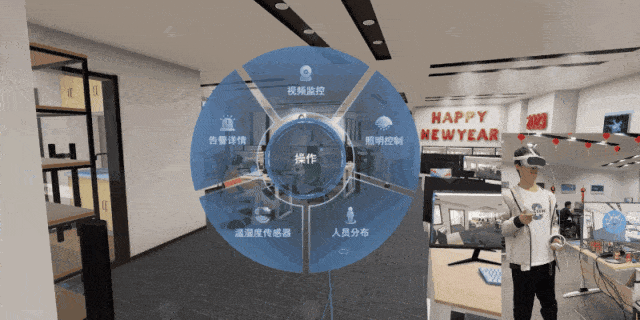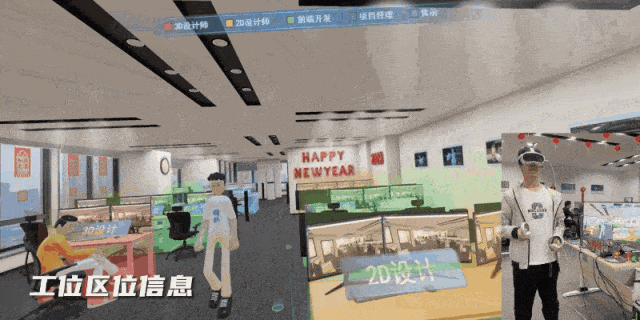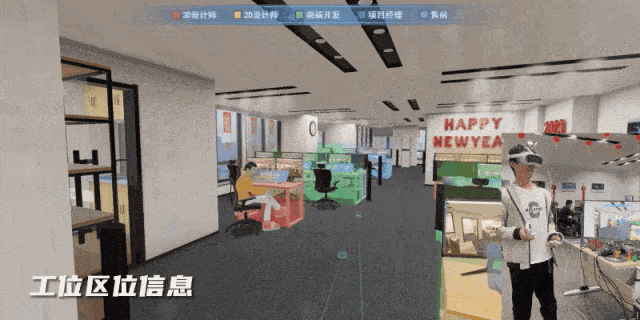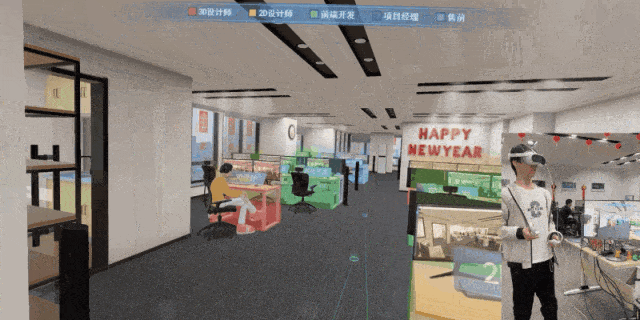
VR 变电站事故追忆反演——正泰电力携手图扑
VR(Virtual Reality，虚拟现实)技术作为近年来快速发展的一项新技术，具有广泛的应用前景，支持融合人工智能、机器学习、大数据等技术，实现更加智能化、个性化的应用。在电力能源领域，VR 技术在高性能计算机和专有设备支…...
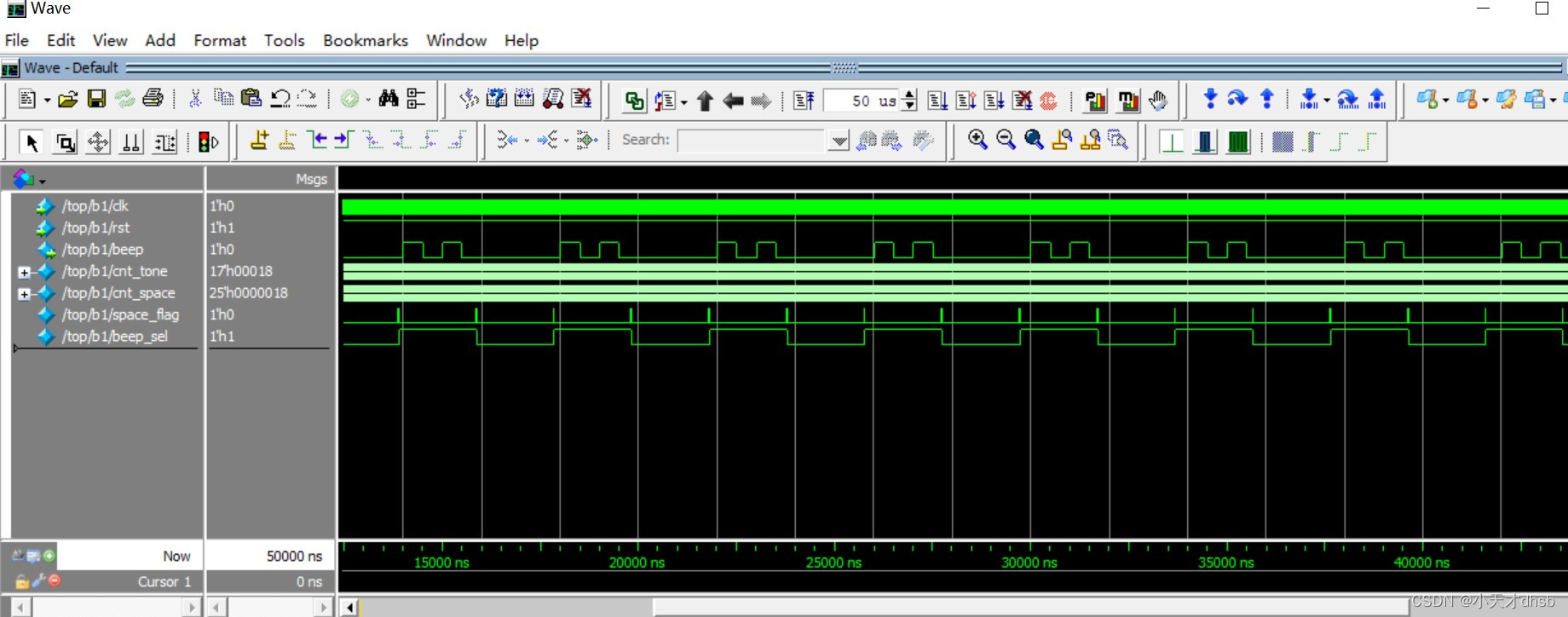
fpga开发——蜂鸣器
蜂鸣器的原理 有源蜂鸣器和无源蜂鸣器 无源蜂鸣器利用电磁感应现象，为音圈接入交变电流后形成的电磁铁与永磁铁相吸或相斥而推动振膜发声，接入直流电只能持续推动振膜而无法产生声音，只能在接通或断开时产生声音。无源蜂鸣器的工作原理与扬声…...
【Liux下6818开发板(ARM)】触摸屏
(꒪ꇴ꒪ ),hello我是祐言博客主页：C语言基础,Linux基础,软件配置领域博主🌍快上🚘，一起学习！送给读者的一句鸡汤🤔：集中起来的意志可以击穿顽石!作者水平很有限，如果发现错误&#x…...
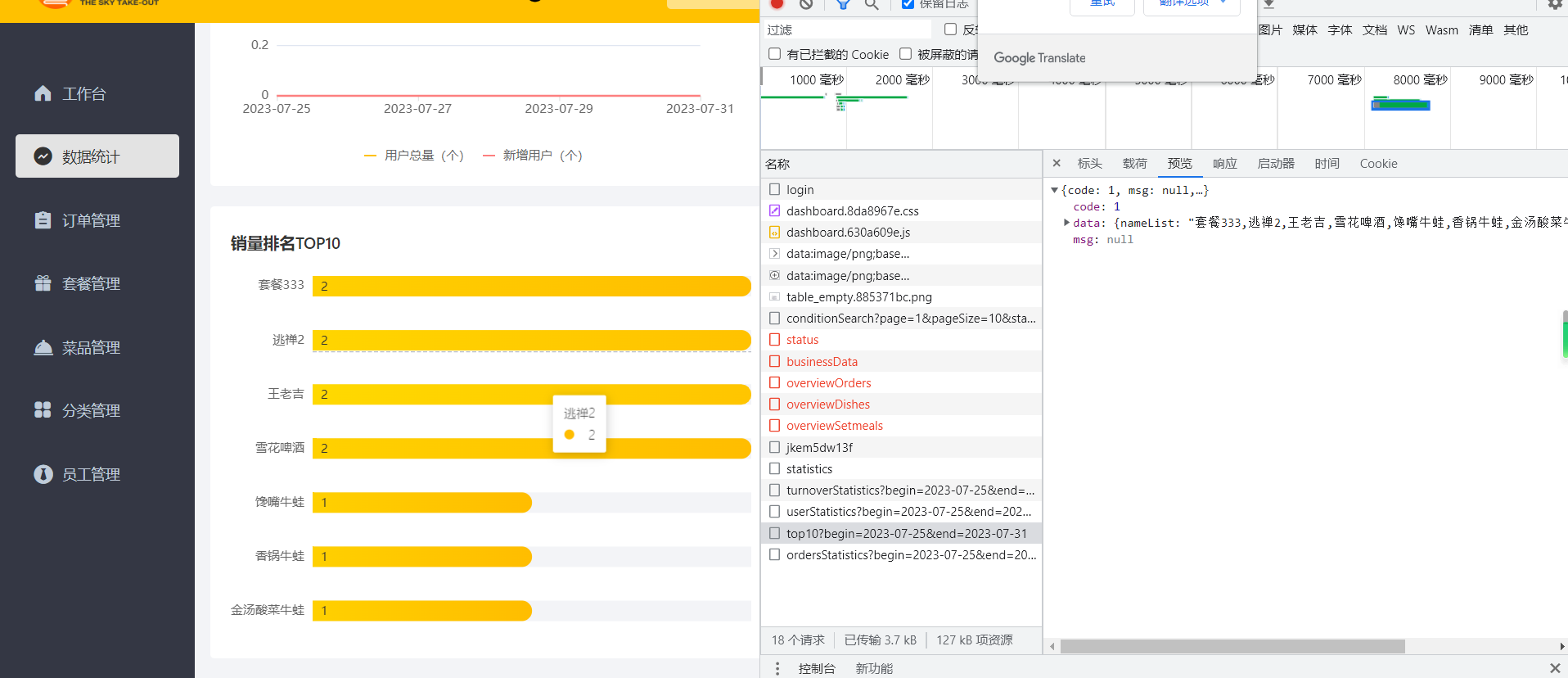
苍穹外卖day11——数据统计图形报表（Apache ECharts）
效果展示 Apache ECharts 介绍 常见图表 入门案例 快速上手 - Handbook - Apache ECharts 营业额统计——需求分析与设计 产品原型 接口设计 VO设计 营业额统计——代码开发 Controller中 /*** 数据统计相关接口*/ RestController RequestMapping("/admin/report&qu…...
在制作PC端Game Launcher游戏启动器时涉及到的技术选型
1）在制作PC端Game Launcher游戏启动器时涉及到的技术选型 2）如何将图片显示到Canvas的Raw Image上面 3）Unity 2018.4.4f1退出重启后出现黑屏 4）如何获取到GPU耗时 这是第346篇UWA技术知识分享的推送，精选了UWA社区…...
SQL力扣练习（九）
目录 1.订单最多的用户(586) 示例 1 解法一(limit) 解法二(dense_rank()) 2.体育馆的人流量 示例 1 解法一(临时表) 解法二（三表法） 1.订单最多的用户(586) 表: Orders --------------------------- | Column Name | Type | ---------…...
软考高级架构师笔记-10数学计算题
目录 1. 前文回顾 & 考情分析2. 最小生成树3. 最短路径4. 网络与最大流量5. 线性规划6. 动态规划/决策表7. 博弈论8. 状态转移矩阵9. 决策论10. 结语1. 前文回顾 & 考情分析 前文回顾： 软考高级架构师笔记-1计算机硬件软考高级架构师笔记-2计算机软件（操作系统）软考…...
)
设计模式五：建造者模式(Builder Pattern)
建造者模式(Builder Pattern)是一种创建型设计模式，用于通过一系列步骤来构建复杂对象。它将对象的构建过程与其表示分离，从而允许相同的构建过程可以创建不同的表示。 建造者模式中的几个角色： 产品(Product)：表示被构建的复杂…...
KubeSphere 容器平台高可用：环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界，看笔记好好学多敲多打，每个人都是大神！ 题目：KubeSphere 容器平台高可用：环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
XCTF-web-easyupload
试了试php，php7，pht，phtml等，都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接，得到flag...
Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning（提示调优） 核心思想：固定预训练模型参数，仅学习额外的连续提示向量（通常是嵌入层的一部分）。实现方式：在输入文本前添加可训练的连续向量（软提示），模型只更新这些提示参数。优势：参数量少（仅提…...
golang循环变量捕获问题
在 Go 语言中，当在循环中启动协程（goroutine）时，如果在协程闭包中直接引用循环变量，可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下： 问题背景 看这个代码片段： fo…...
三维GIS开发cesium智慧地铁教程（5）Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点： 路径验证：确保相对路径.…...
MySQL 隔离级别：脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别，用于控制事务之间的并发访问以及数据的可见性，不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式，具体如下： 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交（READ UNCOMMITTED）允许出现允许…...
【HarmonyOS 5.0】DevEco Testing：鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台，覆盖应用全生命周期测试需求，主要提供五大核心能力： 测试类型检测目标关键指标功能体验基…...
《Playwright：微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络，将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具，支持 Chrome、Firefox、Safari 等主流浏览器，提供多语言 API（Python、JavaScript、Java、.NET）。它的特点包括&a…...
Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文？ 多租户隔离：自动为接入设备追加租户前缀，后端按 ClientID 拆分队列。零代码鉴权：将入站用户名替换为 OAuth Access-Token，后端 Broker 统一校验。灰度发布：根据 IP/地理位写…...