C#常用数学插值法
目录
1、分段线性插值
2、三次样条插值
3、拉格朗日插值
(1)一元全区间不等距插值
(2)一元全区间等距插值
4、埃尔米特插值
(1)埃尔米特不等距插值
(2)埃尔米特等距插值
1、分段线性插值
/// <summary> /// 分段线性插值,将一组数插值为所需点数 /// </summary> /// <param name="dataIn">待插值的数据数组</param> /// <param name="n">插值点数</param> /// <returns>插值后的数据数组</returns> public static float[] Interpolation(float[] dataIn, int n){float[] dataOut = new float[n];int lenIn = dataIn.Length;float[] a = new float[lenIn];float[] divIn = new float[lenIn];float[] divOut = new float[n];divIn[0] = 0;for (int i = 1; i < lenIn; i++){divIn[i] = divIn[i - 1] + 1;}divOut[0] = 0;for (int i = 1; i < n; i++){divOut[i] = divOut[i - 1] + lenIn / (float)n;}int k = 0;for (int i = k; i < n; i++){for (int j = 0; j < lenIn - 1; j++){if (divOut[i] >= divIn[j] && divOut[i] < divIn[j + 1]){dataOut[i] = (dataIn[j + 1] - dataIn[j]) * (divOut[i] - divIn[j]) / (divIn[j + 1] - divIn[j]) + dataIn[j];k = i;}}}return dataOut;}2、三次样条插值
三次样条插值 C#代码实现_c# 三次样条插值_Big_潘大师的博客-CSDN博客
/// <summary>/// 三次样条插值/// </summary>/// <param name="points">排序好的x、y点集合</param>/// <param name="xs">输入x轴数据,插值计算出对应的y轴点</param>/// <param name="chf">写1</param>/// <returns>返回计算好的Y轴数值</returns>public static double[] SplineInsertPoint(PointClass[] points, double[] xs, int chf){int plength = points.Length;double[] h = new double[plength];double[] f = new double[plength];double[] l = new double[plength];double[] v = new double[plength];double[] g = new double[plength];for (int i = 0; i < plength - 1; i++){h[i] = points[i + 1].x - points[i].x;f[i] = (points[i + 1].y - points[i].y) / h[i];}for (int i = 1; i < plength - 1; i++){l[i] = h[i] / (h[i - 1] + h[i]);v[i] = h[i - 1] / (h[i - 1] + h[i]);g[i] = 3 * (l[i] * f[i - 1] + v[i] * f[i]);}double[] b = new double[plength];double[] tem = new double[plength];double[] m = new double[plength];double f0 = (points[0].y - points[1].y) / (points[0].x - points[1].x);double fn = (points[plength - 1].y - points[plength - 2].y) / (points[plength - 1].x - points[plength - 2].x);b[1] = v[1] / 2;for (int i = 2; i < plength - 2; i++){// Console.Write(" " + i);b[i] = v[i] / (2 - b[i - 1] * l[i]);}tem[1] = g[1] / 2;for (int i = 2; i < plength - 1; i++){//Console.Write(" " + i);tem[i] = (g[i] - l[i] * tem[i - 1]) / (2 - l[i] * b[i - 1]);}m[plength - 2] = tem[plength - 2];for (int i = plength - 3; i > 0; i--){//Console.Write(" " + i);m[i] = tem[i] - b[i] * m[i + 1];}m[0] = 3 * f[0] / 2.0;m[plength - 1] = fn;int xlength = xs.Length;double[] insertRes = new double[xlength];for (int i = 0; i < xlength; i++){int j = 0;for (j = 0; j < plength; j++){if (xs[i] < points[j].x)break;}j = j - 1;Console.WriteLine(j);if (j == -1 || j == points.Length - 1){if (j == -1)throw new Exception("插值下边界超出");if (j == points.Length - 1 && xs[i] == points[j].x)insertRes[i] = points[j].y;elsethrow new Exception("插值下边界超出");}else{double p1;p1 = (xs[i] - points[j + 1].x) / (points[j].x - points[j + 1].x);p1 = p1 * p1;double p2; p2 = (xs[i] - points[j].x) / (points[j + 1].x - points[j].x);p2 = p2 * p2;double p3; p3 = p1 * (1 + 2 * (xs[i] - points[j].x) / (points[j + 1].x - points[j].x)) * points[j].y + p2 * (1 + 2 * (xs[i] - points[j + 1].x) / (points[j].x - points[j + 1].x)) * points[j + 1].y;double p4; p4 = p1 * (xs[i] - points[j].x) * m[j] + p2 * (xs[i] - points[j + 1].x) * m[j + 1];// Console.WriteLine(m[j] + " " + m[j + 1] + " " + j);p4 = p4 + p3;insertRes[i] = p4;//Console.WriteLine("f(" + xs[i] + ")= " + p4);}}//Console.ReadLine();return insertRes;}排序计算
public class PointClass{public double x = 0;public double y = 0;public PointClass(){x = 0; y = 0;}//-------写一个排序函数,使得输入的点按顺序排列,是因为插值算法的要求是,x轴递增有序的---------public static PointClass[] DeSortX(PointClass[] points){int length = points.Length;double temx, temy;for (int i = 0; i < length - 1; i++){for (int j = 0; j < length - i - 1; j++)if (points[j].x > points[j + 1].x){temx = points[j + 1].x;points[j + 1].x = points[j].x;points[j].x = temx;temy = points[j + 1].y;points[j + 1].y = points[j].y;points[j].y = temy;}}return points;}}3、拉格朗日插值
(1)一元全区间不等距插值
/// <summary>/// 一元全区间不等距插值/// 拉格朗日插值算法/// </summary>/// <param name="x">一维数组,长度为n,存放给定的n个结点的值x(i),要求x(0)<x(1)<...<x(n-1)</param>/// <param name="y">一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1</param>/// <param name="t">存放指定的插值点的x值</param>/// <returns>指定的查指点t的函数近似值y=f(t)</returns>public static double Lagrange(double[] x, double[] y, double t){// x,y点数int n = x.Length;double z = 0.0;// 特例处理if (n < 1){return (z);}else if (n == 1){z = y[0];return (z);}else if (n == 2){z = (y[0] * (t - x[1]) - y[1] * (t - x[0])) / (x[0] - x[1]);return (z);}// 开始插值int ik = 0;while ((x[ik] < t) && (ik < n)){ik = ik + 1;}int k = ik - 4;if (k < 0){k = 0;}int m = ik + 3;if (m > n - 1){m = n - 1;}for (int i = k; i <= m; i++){double s = 1.0;for (int j = k; j <= m; j++){if (j != i){// 拉格朗日插值公式s = s * (t - x[j]) / (x[i] - x[j]);}}z = z + s * y[i];}return (z);} /// <summary>/// 一元全区间不等距插值/// </summary>/// <param name="points">点集(含XY坐标)</param>/// <param name="t"></param>/// <returns></returns>public static double Lagrange(PointF[] points, double t){double[] x = new double[points.Length];double[] y = new double[points.Length];for (int i = 0; i < points.Length; i++){x[i] = points[i].X;y[i] = points[i].Y;}return Lagrange(x, y, t);} /// <summary>/// 一元全区间不等距插值/// </summary>/// <param name="points">二元组类型的点集(含XY坐标)</param>/// <param name="t"></param>/// <returns></returns>public static double Lagrange(List<Tuple<double, double>> points, double t){double[] x = new double[points.Count];double[] y = new double[points.Count];for (int i = 0; i < points.Count; i++){x[i] = points[i].Item1;y[i] = points[i].Item2;}return Lagrange(x, y, t);} /// <summary>/// 一元全区间不等距插值,获得插值后的曲线(折线拟合)数据/// </summary>/// <param name="points">点集(含XY坐标)</param>/// <param name="segment_count">每数据段的分割数</param>/// <returns></returns>public static PointF[] Lagrange_Curve(PointF[] points, int segment_count = 10){int n = points.Length;PointF[] segments = new PointF[n * segment_count + 1];for (int i = 0; i < points.Length - 1; i++){double dt = (points[i + 1].X - points[i].X) / segment_count;double t = points[i].X;for (int j = 0; j <= segment_count; j++, t += dt){PointF p = new PointF(0.0F, 0.0F);p.X = (float)t;if (j == 0) p.Y = points[i].Y;else if (j == segment_count) p.Y = points[i + 1].Y;else p.Y = (float)(Lagrange(points, t));segments[i] = p;}}return segments;} /// <summary>/// 一元全区间等距插值/// (使用非等距插值的方法)/// </summary>/// <param name="x0">存放等距n个结点中第一个结点的值</param>/// <param name="step">等距结点的步长</param>/// <param name="y">一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1</param>/// <param name="t">存放指定的插值点的x值</param>/// <returns>指定的查指点t的函数近似值y=f(t)</returns>public static double Lagrange(double x0, double step, double[] y, double t){double[] x = new double[y.Length];for (int i = 0; i < y.Length; i++, x0 += step){x[i] = x0;}return Lagrange(x, y, t);}(2)一元全区间等距插值
/// <summary>/// 一元全区间等距插值/// </summary>/// <param name="x0">存放等距n个结点中第一个结点的值</param>/// <param name="step">等距结点的步长</param>/// <param name="y">一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1</param>/// <param name="t">存放指定的插值点的x值</param>/// <returns>指定的查指点t的函数近似值y=f(t)</returns>public static double Lagrange_Equidistant(double x0, double step, double[] y, double t){int n = y.Length;double z = 0.0;// 特例处理if (n < 1){return (z);}else if (n == 1){z = y[0];return (z);}else if (n == 2){z = (y[1] * (t - x0) - y[0] * (t - x0 - step)) / step;return (z);}// 开始插值int ik = 0;if (t > x0){double p = (t - x0) / step;ik = (int)p;double q = (float)ik;if (p > q){ik = ik + 1;}}else{ik = 0;}int k = ik - 4;if (k < 0){k = 0;}int m = ik + 3;if (m > n - 1){m = n - 1;}for (int i = k; i <= m; i++){double s = 1.0;double xi = x0 + i * step;for (int j = k; j <= m; j++){if (j != i){double xj = x0 + j * step;// 拉格朗日插值公式s = s * (t - xj) / (xi - xj);}}z = z + s * y[i];}return (z);}4、埃尔米特插值
(1)埃尔米特不等距插值
/// <summary>/// 埃尔米特不等距插值/// </summary>/// <param name="x">一维数组,长度为n,存放给定的n个结点的值x(i),要求x(0)<x(1)<...<x(n-1)</param>/// <param name="y">一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1</param>/// <param name="dy">一维数组,长度为n,存放给定的n个结点的函数导数值y'(i),y'(i) = f'(x(i)), i=0,1,...,n-1</param>/// <param name="t">存放指定的插值点的x值</param>/// <returns>指定的查指点t的函数近似值y=f(t)</returns>public static double Hermite(double[] x, double[] y, double[] dy, double t){int n = x.Length;double z = 0.0;// 循环插值for (int i = 1; i <= n; i++){double s = 1.0;for (int j = 1; j <= n; j++){if (j != i){s = s * (t - x[j - 1]) / (x[i - 1] - x[j - 1]);}}s = s * s;double p = 0.0;for (int j = 1; j <= n; j++){if (j != i){p = p + 1.0 / (x[i - 1] - x[j - 1]);}}double q = y[i - 1] + (t - x[i - 1]) * (dy[i - 1] - 2.0 * y[i - 1] * p);z = z + q * s;}return (z);} /// <summary>/// 埃尔米特等距插值/// (使用非等距插值的方法)/// </summary>/// <param name="x0">存放等距n个结点中第一个结点的值</param>/// <param name="step">等距结点的步长</param>/// <param name="y">一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1</param>/// <param name="dy">一维数组,长度为n,存放给定的n个结点的函数导数值y'(i),y'(i) = f'(x(i)), i=0,1,...,n-1</param>/// <param name="t">存放指定的插值点的x值</param>/// <returns>指定的查指点t的函数近似值y=f(t)</returns>public static double Hermite(double x0, double step, double[] y, double[] dy, double t){double[] x = new double[y.Length];for (int i = 0; i < y.Length; i++, x0 += step){x[i] = x0;}return Hermite(x, y, dy, t);}(2)埃尔米特等距插值
/// <summary>/// 埃尔米特等距插值/// </summary>/// <param name="x0">等距n个结点中第一个结点的值</param>/// <param name="step">等距结点的步长</param>/// <param name="y">一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1</param>/// <param name="dy">一维数组,长度为n,存放给定的n个结点的函数导数值y'(i),y'(i) = f'(x(i)), i=0,1,...,n-1</param>/// <param name="t">存放指定的插值点的x值</param>/// <returns>指定的查指点t的函数近似值y=f(t)</returns>public static double Hermite(double x0, double step, double[] y, double[] dy, double t){int n = y.Length;double z = 0.0;// 循环插值for (int i = 1; i <= n; i++){double s = 1.0;double q = x0 + (i - 1) * step;double p;for (int j = 1; j <= n; j++){p = x0 + (j - 1) * step;if (j != i){s = s * (t - p) / (q - p);}}s = s * s;p = 0.0;for (int j = 1; j <= n; j++){if (j != i){p = p + 1.0 / (q - (x0 + (j - 1) * step));}}q = y[i - 1] + (t - q) * (dy[i - 1] - 2.0 * y[i - 1] * p);z = z + q * s;}return (z);}相关文章:

C#常用数学插值法
目录 1、分段线性插值 2、三次样条插值 3、拉格朗日插值 (1)一元全区间不等距插值 (2)一元全区间等距插值 4、埃尔米特插值 (1)埃尔米特不等距插值 (2)埃尔米特等距插值 1、…...
ELK日志管理平台架构和使用说明
一、部署架构 二、服务注册 2.1 日志解析服务 服务名:日志解析服务(Logstash) 服务默认端口:9600 2.2 日志查询服务 服务名:日志查询服务(Kibana) 服务默认端口:5601 三、对接…...

抖音短视频seo矩阵系统源码开发部署技术分享
抖音短视频的SEO矩阵系统是一个非常重要的部分,它可以帮助视频更好地被搜索引擎识别和推荐。以下是一些关于开发和部署抖音短视频SEO矩阵系统的技术分享: 一、 抖音短视频SEO矩阵系统的技术分享: 关键词研究:在开发抖音短视频SEO矩…...

docker 部署一个单节点的rocketmq
拉取镜像 sudo docker pull rocketmqinc/rocketmq创建数据挂载目录 mkdir -p /docker/rocketmq/data/namesrv/logs mkdir -p /docker/rocketmq/data/namesrv/store mkdir -p /docker/rocketmq/data/broker/logs mkdir -p /docker/rocketmq/data/broker/store /docker/…...

MySQL优化
目录 一. 优化 SQL 查询语句 1.1. 分析慢查询日志 1.2. 优化 SQL 查询语句的性能 1.2.1 优化查询中的索引 1.2.2 减少表的连接(join) 1.2.3 优化查询语句中的过滤条件 1.2.4 避免使用SELECT * 1.2.5 优化存储过程和函数 1.2.6 使用缓存 二. 优化表结构…...
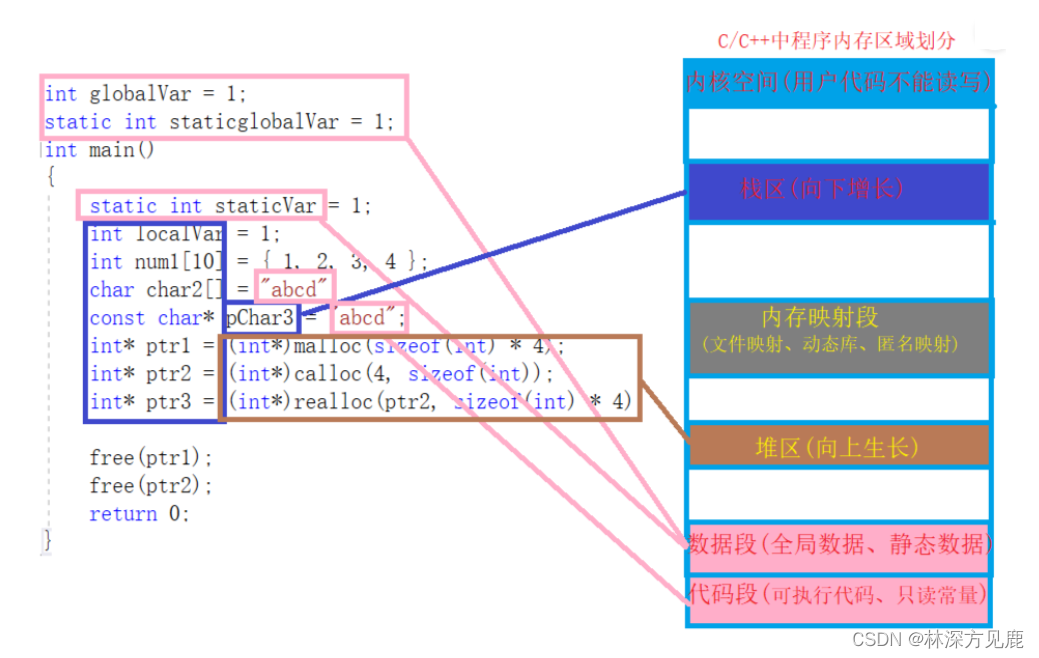
【C++】总结9
文章目录 C从源代码到可执行程序经过什么步骤静态链接和动态链接类的对象存储空间C的内存分区内存池在成员函数中调用delete this会出现什么问题?如果在类的析构函数中调用delete this,会发生什么? C从源代码到可执行程序经过什么步骤 预处理…...

C++报错 XX does not name a type;field `XX’ has incomplete type解决方案
C报错 XX does not name a type;field XX’ has incomplete type解决方案 两个C编译错误及解决办法–does not name a type和field XX’ has incomplete type 编译错误一:XX does not name a type 编译错误二:field XX’ has incomplete t…...

28.利用fminsearch、fminunc 求解最大利润问题(matlab程序)
1.简述 1.无约束(无条件)的最优化 fminunc函数 : - 可用于任意函数求最小值 - 统一求最小值问题 - 如求最大值问题: >对函数取相反数而变成求最小值问题,最后把函数值取反即为函数的最大值。 使用格式如下 1.必须预先把函数存…...

图像 检测 - FCOS: Fully Convolutional One-Stage Object Detection (ICCV 2019)
FCOS: Fully Convolutional One-Stage Object Detection - 全卷积一阶段目标检测(ICCV 2019) 摘要1. 引言2. 相关工作3. 我们的方法3.1 全卷积一阶目标检测器3.2 FCOS的FPN多级预测3.3 FCOS中心度 4. 实验4.1 消融研究4.1.1 FPN多级预测4.1.2 有无中心度…...
C# NDArray System.IO.FileLoadException报错原因分析
C# NDArray System.IO.FileLoadException 报错原因分析: 1.NuGet程序包版本有冲突 2.统一项目版本 1.打开解决方案NuGet程序包设置 2.查看是否有版本冲突 3.统一版本冲突...

快速响应,上门维修小程序让您享受无忧生活
随着科技的不断发展和智能手机的普及,上门维修小程序成为了现代人生活中越来越重要的一部分。上门维修小程序通过将维修服务与互联网相结合,为用户提供了更加便捷、高效的维修服务体验。下面将介绍上门维修小程序开发的优势。 提供便捷的预约方式&am…...
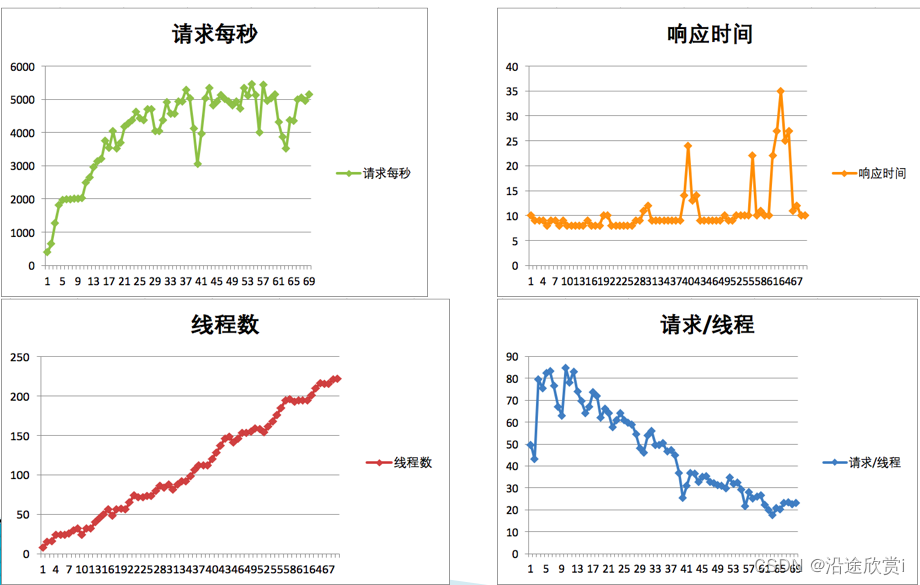
05、性能分析思路?
工具操作:包括压力工具、监控工具、剖析工具、调试工具。数值理解:包括上面工具中所有输出的数据。趋势分析、相关性分析、证据链分析:就是理解了工具产生的数值之后,还要把它们的逻辑关系想明白。这才是性能测试分析中最重要的一…...
【编程语言 · C语言 · calloc和realloc】
【编程语言 C语言 calloc和realloc】https://mp.weixin.qq.com/s?__bizMzg4NTE5MDAzOA&mid2247491544&idx1&sn72d8f9931cfa7ce7441a3248475ab619&chksmcfade321f8da6a374a5935bb46441a03a007c0589db6b8afa8c1991854d632a3201553e37b0b&payreadticketHGy…...

机器学习分布式框架ray运行pytorch实例
Ray是一个用于分布式计算的开源框架,它可以有效地实现并行化和分布式训练。下面是使用Ray来实现PyTorch的训练的概括性描述: 安装Ray:首先,需要在计算机上安装Ray。你可以通过pip或conda来安装Ray库。 准备数据:在使用…...
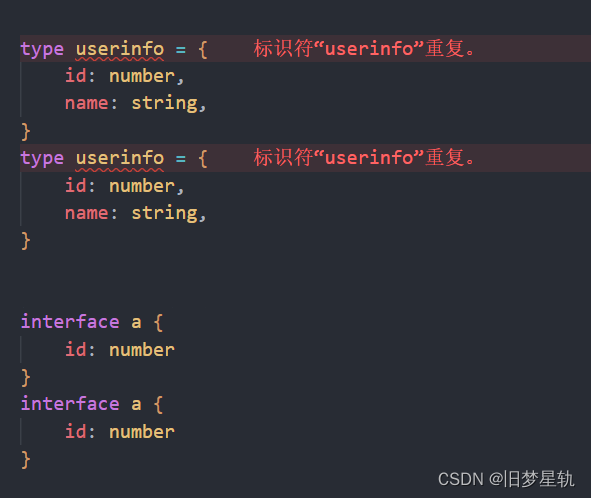
TypeScript 【type】关键字的进阶使用方式
导语: 在前面章节中,我们了解到 TS 中 type 这个关键字,常常被用作于,定义 类型别名,用来简化或复用复杂联合类型的时候使用。同时也了解到 为对象定义约束接口类型 的时候所使用的是 Interfaces。 其实对于前面&#…...
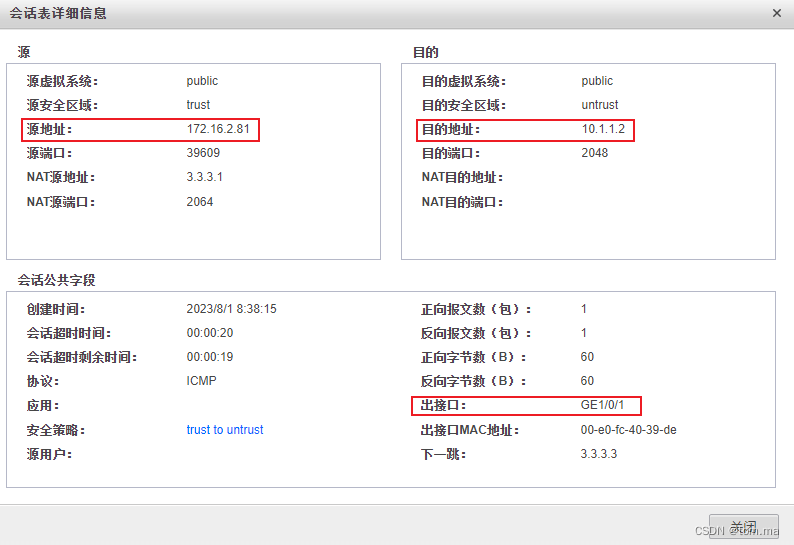
策略路由实现多ISP接入Internet
组网需求: 企业分别从ISP1和ISP2租用了一条链路 PC3用户上网访问Server1时走ISP1PC4用户上网访问Server1时走ISP2 拓扑图 一、ISP1 运营商 R1路由器 <Huawei>sys [Huawei]sys R1 [R1]un in en[R1]int g0/0/0 [R1-GigabitEthernet0/0/0]ip addr 2.2.2.2 2…...

Socket本质、实战演示两个进程建立TCP连接通信的过程
文章目录 Socket是什么引入面试题, 使你更深刻的理解四元组 Socket网络通信大体流程实战演示TCP连接建立过程需要用到的linux 查看网络的一些命令测试的程序一些准备工作启动服务端, 并没有调用accept启动客户端开启服务accept Socket是什么 通俗来说,Socket是套接字,是一种编…...

java学习路程之篇四、进阶知识、石头迷阵游戏、绘制界面、打乱石头方块、移动业务、游戏判定胜利、统计步数、重新游戏
文章目录 1、绘制界面2、打乱石头方块3、移动业务4、游戏判定胜利5、统计步数6、重新游戏7、完整代码 1、绘制界面 2、打乱石头方块 3、移动业务 4、游戏判定胜利 5、统计步数 6、重新游戏 7、完整代码 java之石头迷阵单击游戏、继承、接口、窗体、事件、组件、按钮、图片...
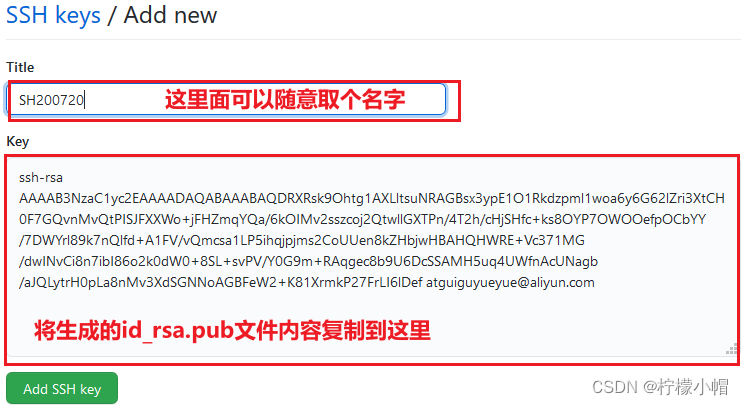
Git全栈体系(三)
第六章 GitHub 操作 一、创建远程仓库 二、远程仓库操作 命令名称作用git remote -v查看当前所有远程地址别名git remote add 别名 远程地址起别名git push 别名 分支推送本地分支上的内容到远程仓库git clone 远程地址将远程仓库的内容克隆到本地git pull 远程库地址别名 远…...
JMeter发送get请求并分析返回结果
在实际工作的过程中,我们通常需要模拟接口,来进行接口测试,我们可以通过JMeter、postman等多种工具来进行接口测试,但是工具的如何使用对于我们来说并不是最重要的部分,最重要的是设计接口测试用例的思路与分析结果的能…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
