管理类联考——逻辑——形式逻辑——汇总篇
简述
形式逻辑:
- 识别题型:逻辑符号表达及标志词:联假言符号化+特殊命题“除非否则”;
- 五大关系:矛盾、等价、包含、至少有一真、至少有一假;【通过“关系”,串联起“假联选”言】
识别题型:逻辑符号表达及标志词
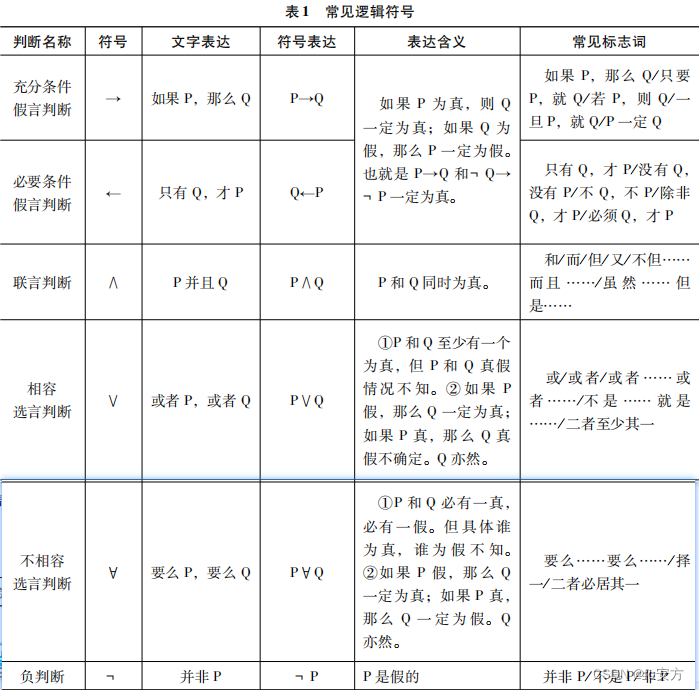
在应试时,“ → ” 和 “ ← ”的符号一般都习惯用 “ → ” 来进行统一表达,因此P → Q和Q ← P是等价的,也就意味着,“如果Р,那么Q” = “只有Q,才P”,都可以用“P → Q”来表达。
请将下列语句用符号来表达。
(1)知无不言,言无不尽。
(2)德才兼备。
(3)虽然你成绩不太好,但是你也不能自暴自弃。
(4)宋玉和潘安都是男神。
(5)他既大方又稳重。
(6)考研不但时间要抓紧,而且效率也要高。
(7)他一面若无其事,一面暗自神伤。
(8)夕阳西下,断肠人在天涯。
(9)可能晚上吃米饭,也可能吃蔬菜沙拉。
(10)一个成功人士的才华和气质至少得有一个特别出众。
(11)这次没考好,也许是题目太难,也许是状态不佳。
(12)学习委员从张三和李四择一担任。
(13)但凡成功者天赋和努力二者必居其一。
(14)人要真诚,也要善良。
(15)明天或者刮风,或者下雨。
(16)要么考研,要么考公务员。
(17)如果找到真爱,那么懂得真爱。
(18)若找到真爱,则懂得真爱。
(19)一旦找到真爱,则懂得真爱。
(20)只要找到真爱,就懂得真爱。
(21)必须懂得真爱,才能找到真爱。
(22)只有懂得真爱,才能找到真爱。
(23)不懂得真爱,不能找到真爱。
(24)除非懂得真爱,才能找到真爱。
(25)除非懂得真爱,否则不能找到真爱。
(26)除非懂得真爱,否则能找到真爱。
(27)除非不懂得真爱,否则能找到真爱。
(28)找到真爱,除非懂得真爱。
(29)懂得真爱,否则找到真爱。
(30)并非张珊是成功人士。【精点解析】
(1)表示同时为真,即:知无不言∧言无不尽。
(2)根据标志词“兼备”表示“且”,即:德 ∧ 才。
(3)根据标志词“虽然……但是……”表示“且”,即:成绩不太好 ∧ 不能自暴自弃。
(4)根据标志词“都是”表示“且”,即:宋玉是男神 ∧ 潘安是男神。
(5)根据标志词“既……又……”表示“且”,即:大方 ∧ 稳重。
(6)根据标志词“不但……而且……”表示“且”,即:考研时间要抓紧 ∧ 效率要高。
(7)根据标志词“一面……一面……”表示“且”,即:他若无其事 ∧ 暗自神伤。
(8)表示同时为真,即:夕阳西下 ∧ 断肠人在天涯。
(9)根据标志词“可能……也可能……”表示“或”,可能存在晚上同时吃米饭和蔬菜沙拉的可能,表示P V Q,即:晚上吃米饭 V 晚上吃蔬菜沙拉。
(10)根据标志词“至少有一个”表示“或”,即:一个成功人士的才华特别出众 V 气质特别出众。
(11)根据标志词“也许……也许……”表示“或”,即:这次没考好,题目太难 V 状态不佳。
(12)根据标志词“择一”表示“要么……要么……”,即:张三担任学习委员 ∀ 李四担任学习委员。
(13)根据标志词“必居其一”表示“要么……要么……”,即:成功者有天赋 ∀ 有努力。
(14)根据标志词“也”表示“且”,即:人要真诚 ∧ 人要善良。
(15)根据标志词“或者……或者……”表示“或”,即:明天刮风 V 明天下雨。
(16)根据标志词“要么……要么……”即:考研 ∀ 考公务员。
(17)根据标志词“如果P,那么Q”表示“P→Q”,即:找到真爱→懂得真爱。
(18)根据标志词“若P,则Q”表示“P→Q”,即:找到真爱→懂得真爱。
(19)根据标志词“一旦P,就Q”表示“P→Q”,即:找到真爱→懂得真爱。
(20)根据标志词“只要P,就Q”表示“P→Q”,即:找到真爱→懂得真爱。
(21)根据标志词“必须Q,才P”表示“P→Q”,即:能找到真爱→懂得真爱。
(22)根据标志词“只有Q,才P”表示“P→Q”,即:能找到真爱→懂得真爱。
(23)根据标志词“不Q,不P”表示“P→Q”,即:能找到真爱→懂得真爱。
(24)根据标志词“除非Q,才P”表示“P→Q”,即:能找到真爱→懂得真爱。
(25)根据标志词“除非Q,否则不P”表示“┐Q→┐P”,即:不懂得真爱→不能找到真爱。
(26)根据标志词“除非Q,否则P”表示“┐Q→P”,即:不懂得真爱→能找到真爱。
(27)根据标志词“除非Q,否则P”表示“┐Q→P”,即:懂得真爱→能找到真爱。
(28)根据标志词“P,除非Q”表示“┐P→Q”,即:找不到真爱→懂得真爱。
(29)根据标志词“P,否则Q”表示“┐P→Q”,即:找不到真爱→懂得真爱。
(30)根据标志词“并非P”,即:┐张珊是成功人士 = 张珊不是成功人士。
难点:除非Q,否则P
考生注意:“→”表示的假言判断有常见的三种特殊结构,如下:
- 除非Q,否则P。“否则”的逻辑表达所包含的两个词“否”和“则”(除非,除表示否定,非表示否定,双重否定表肯定),正好分别对应于“┐”和“→”。因此“除非Q,否则P”的意思是“如果否定Q,则P”,即┐Q→P。同理可知,“除非Q,否则不P”=┐Q→┐P。如(25)(26)(27)小题。
- P,否则Q。这样的结构需要记住,“否”是否“否则”前面的断定;“则”是则“否则”后面的断定。因此“P,否则Q”的意思也是“如果否定Р,则Q”,即┐P→Q。如(29)小题。
- P,除非Q。这样的结构其实是省略了“否则”,补充完整应该是“除非Q,否则P”。意思是“如果否定Q,则P”,即┐P→Q。如(28)小题。由于假言判断推理可取逆否等价,故:┐Q→P=┐P→Q; ┐Q→┐P = P→Q。考生注意将( 17) ~ (29)小题综合起来理解。
形式逻辑五大关系
一、矛盾关系
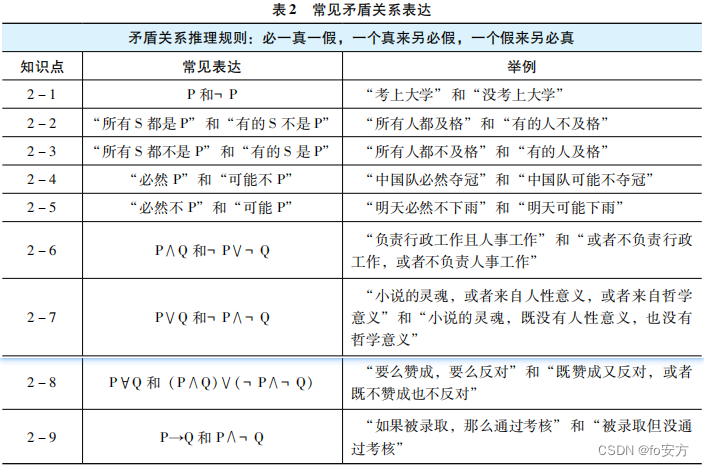
二、等价关系
常见等价关系表
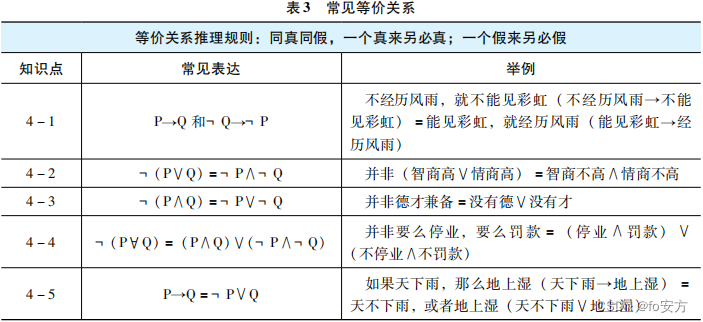
等价公式
- 假言
(1) P → Q = ┐ Q → ┐ P P→Q=┐ Q→┐ P P→Q=┐Q→┐P
(2) P ↔ Q = ( P ∧ Q ) ∨ ( ┐ P ∧ ┐ Q ) P↔Q=(P∧Q)∨(┐ P∧┐ Q) P↔Q=(P∧Q)∨(┐P∧┐Q)
(3) ┐ ( P ↔ Q ) = ( P ∧ ┐ Q ) ∨ ( ┐ P ∧ Q ) ┐ (P↔Q)=(P∧┐ Q)∨(┐ P∧Q) ┐(P↔Q)=(P∧┐Q)∨(┐P∧Q) - 联言选言
(1) ┐ ( P ∨ Q ) = ┐ P ∧ ┐ Q ┐ (P∨Q)=┐ P∧┐ Q ┐(P∨Q)=┐P∧┐Q
(2) ┐ ( P ∧ Q ) = ┐ P ∨ ┐ Q ┐ (P∧Q)=┐ P∨┐ Q ┐(P∧Q)=┐P∨┐Q
(3) P ∨ Q = ( P ∧ ┐ Q ) ∨ ( ┐ P ∧ Q ) P∨Q=(P∧┐ Q)∨(┐ P∧Q) P∨Q=(P∧┐Q)∨(┐P∧Q)
(4) ┐ ( P ∨ Q ) = ( P ∧ Q ) ∨ ( ┐ P ∧ ┐ Q ) ┐ (P∨Q)=(P∧Q)∨(┐ P∧┐ Q) ┐(P∨Q)=(P∧Q)∨(┐P∧┐Q) - 或则转化
(1) P ∨ Q = ┐ P → Q = ┐ Q → P P∨Q=┐P→Q=┐Q→P P∨Q=┐P→Q=┐Q→P
(2) P → Q = ┐ ( P ∧ ┐ Q ) = ┐ P ∨ Q P→Q=┐(P∧┐Q)=┐P∨Q P→Q=┐(P∧┐Q)=┐P∨Q
注意:若出现“或”,且题干不涉及真假,优先将“或”变“推”。题干涉及真假,若没有“推”与“且”这一组矛盾,优先将“则”转成“或”。 - 递推推理
A → B , B → C ,所以 A → B → C A→B,B→C,所以A→B→C A→B,B→C,所以A→B→C - 做题思路
观察“→”的个数
(1)1个,考查自身,考查逆否等价,或者逻辑标志词的转化。
(2)多个,能串则串,比照选项,注意首尾;不能串,一一比照选项,往往是某一句的等值。
三、包含关系
∩ ∪ ∧ ∨ ⊃ ⊂ ∅ ⟺ ┐ ∀ ∞ σ ∈ ± ∓ ↔
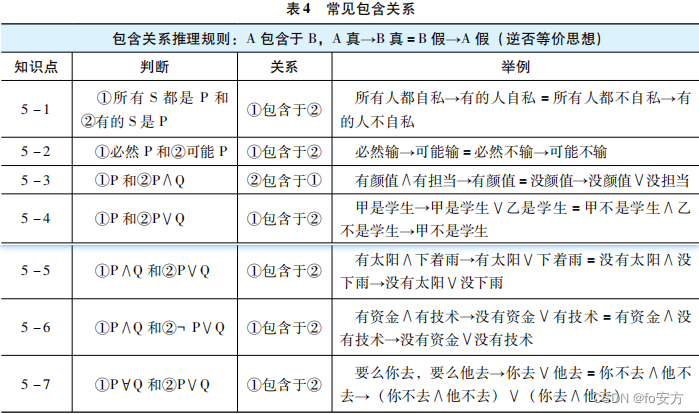
考生注意:
1.“有的S是P”表示至少有一个S是P,至多全部的S都是P,因此“所有S都是P”是“有的S是P”为真时的一种可能,故“所有S都是P”包含于“有的S是P”。
2.同理可知,“可能P”表示发生概率大于0、小于等于100%,因此,“必然P”是“可能P”为真时的一种可能,故“必然P”包含于“可能P”。
四、至少有一真的关系
若A和B属于至少有一真的关系,就意味着A和B至少有一个为真,可能有一个真,也可能两个都是真的;如果一个是真,那么另一个无法判断;如果一个是假,那么另一个为真。
至少有一假的关系
若A和B属于至少有一假的关系,就意味着A和B至少有一个为假,可能有一个假,也可能两个都是假的;如果一个是假,那么另一个无法判断;如果一个是真,那么另一个为假。

相关文章:

管理类联考——逻辑——形式逻辑——汇总篇
简述 形式逻辑: 识别题型:逻辑符号表达及标志词:联假言符号化特殊命题“除非否则”;五大关系:矛盾、等价、包含、至少有一真、至少有一假;【通过“关系”,串联起“假联选”言】 识别题型&…...

架构的分类
目录 一、 RUP41 架构 1.1 RUP41架构方法概述 1.2 RUP41架构总体 1.3 RUP41架构方法内容 1.3.1 逻辑视图 1.3.2 开发视图 1.3.3 物理视图 1.3.4 处理视图 1.3.5 场景视图 二、 TOGAF9 架构 2.1 TOGAF9 架构概述 2.2 TOGAF9 架构分类 2.2.1 业务架构 2.2.2 数据架…...

[SQL挖掘机] - 窗口函数 - lag
介绍: lag() 是一种常用的窗口函数,它用于获取某一行之前的行的值。它可以用来在结果集中的当前行之前访问指定列的值。 用法: lag() 函数的语法如下: lag(列名, 偏移量, 默认值) over (partition by 列名1, 列名2, ... order by 列名 [asc|desc], .…...

springboot项目如何自动重启(使用Devtools检测修改并自动重启springboot)
1. 问题: 我们在项目开发阶段,可能经常会修改代码,修改完后就要重启Spring Boot。经常手动停止再启动,比较麻烦。 所以我们引入一个Spring Boot提供的开发工具; 只要源码或配置文件发生修改,Spring Boot应用…...
docker: Error response from daemon: No command specified.
执行 docker run -it -d -v /home/dell/workspace/workspace/test_192.168.1.202_pipeline:/home/workspace1 --name test_192.168.1.202_pipeline_10 qnx:7.1报错 问题定位:export导入的镜像需要带上command,以下命令查看command信息 docker ps --no…...

百度地图点标记加调用
先看效果 PHP代码 <?phpnamespace kds_addons\edata\controller;use think\addons\Controller; use think\Db;class Maps extends Controller {// 经纬度计算面积function calculate_area($points){$totalArea 0;$numPoints count($points);if ($numPoints > 2) {f…...
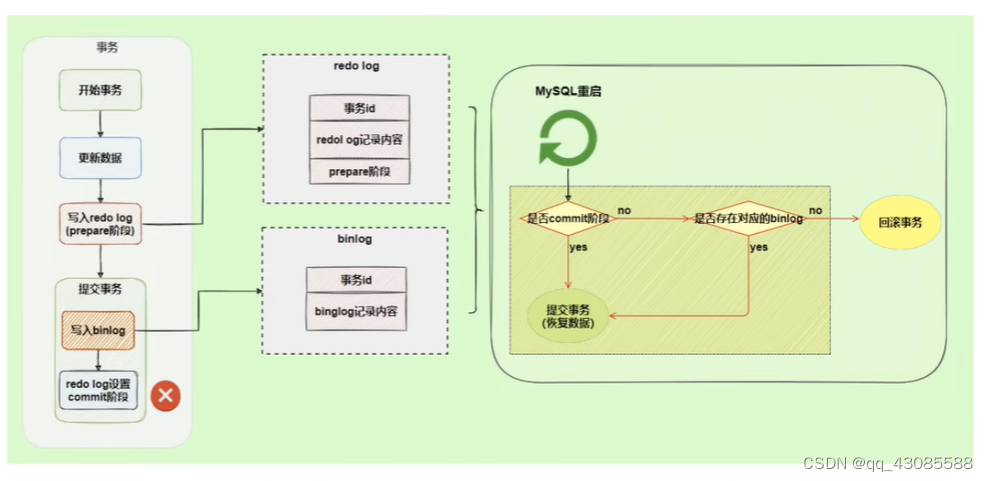
MySQL 其他数据库日志
我们了解数据库事务时,知道两种日志:重做日志,回滚日志。 对于线上数据库应用系统,突然遭遇 数据库宕机 怎么办?在这种情况下,定位宕机的原因 就非常关键。我们可以查看数据库的 错误日志。因为日志中记录…...

为何企业和开发团队应该重视进行兼容性测试
随着科技的不断进步和软件的广泛应用,保证软件在不同平台和环境下正常运行变得至关重要。本文将探讨软件兼容性测试的重要性和好处,并介绍为何企业和开发团队应该重视进行兼容性测试,以确保软件的稳定性和用户体验。 提供用户友好的体验 软件…...

牛客网Verilog刷题——VL51
牛客网Verilog刷题——VL51 题目答案 题目 请编写一个十六进制计数器模块,计数器输出信号递增每次到达0,给出指示信号zero,当置位信号set 有效时,将当前输出置为输入的数值set_num。模块的接口信号图如下: 模块的时序图…...

从零实现深度学习框架——Transformer从菜鸟到高手(一)
引言 💡本文为🔗[从零实现深度学习框架]系列文章内部限免文章,更多限免文章见 🔗专栏目录。 本着“凡我不能创造的,我就不能理解”的思想,系列文章会基于纯Python和NumPy从零创建自己的类PyTorch深度学习框…...
数组指针
数组指针的定义 1.数组指针是指针还是数组? 指针。 int a 10;int* p &a;//指向整型数据的指针 char b w;char* q &b;//指向字符变量的指针 所以数组指针应该是指向数组的指针。 2.数组指针应该怎么定义? int arr[10] { 0 };int(*p)[10] …...

C++设计模式之过滤器设计模式
C过滤器设计模式 什么是过滤器设计模式 过滤器设计模式是一种行为型设计模式,它允许你在特定的条件下对输入或输出进行过滤,以便实现不同的功能。 该模式有什么优缺点 优点 可扩展性:过滤器设计模式允许您轻松地添加、删除或替换过滤器&a…...
)
SpringBoot整合RedisTemplate操作Redis数据库详解(提供Gitee源码)
前言:简单分享一下我在实际开发当中如何使用SpringBoot操作Redis数据库的技术分享,完整的代码我都提供了出来,大家按需复制使用即可! 目录 一、导入pom依赖 二、yml配置文件 三、使用FastJson序列化 四、核心配置类 五、工具…...

SQL 执行计划管理(SPM)
一、SPM 需求背景 任何数据库应用程序的性能在很大程度上都依赖于查询执行,尽管优化器无需用户干预就可以评估最佳计划,但是 SQL 语句的执行计划仍可能由于以下多种原因发生意外更改:版本升级、重新收集优化器统计信息、改变优化器参数或模式…...
浅谈微服务异步解决方案
导言 异步是一种设计思想,不是设计目的,因此不要为了异步而异步,要有所为,有所不为。 异步不是『银弹』, 避免试图套用一个『异步框架』解决所有问题, 需要根据不同的业务特点或要求,选择合适的…...
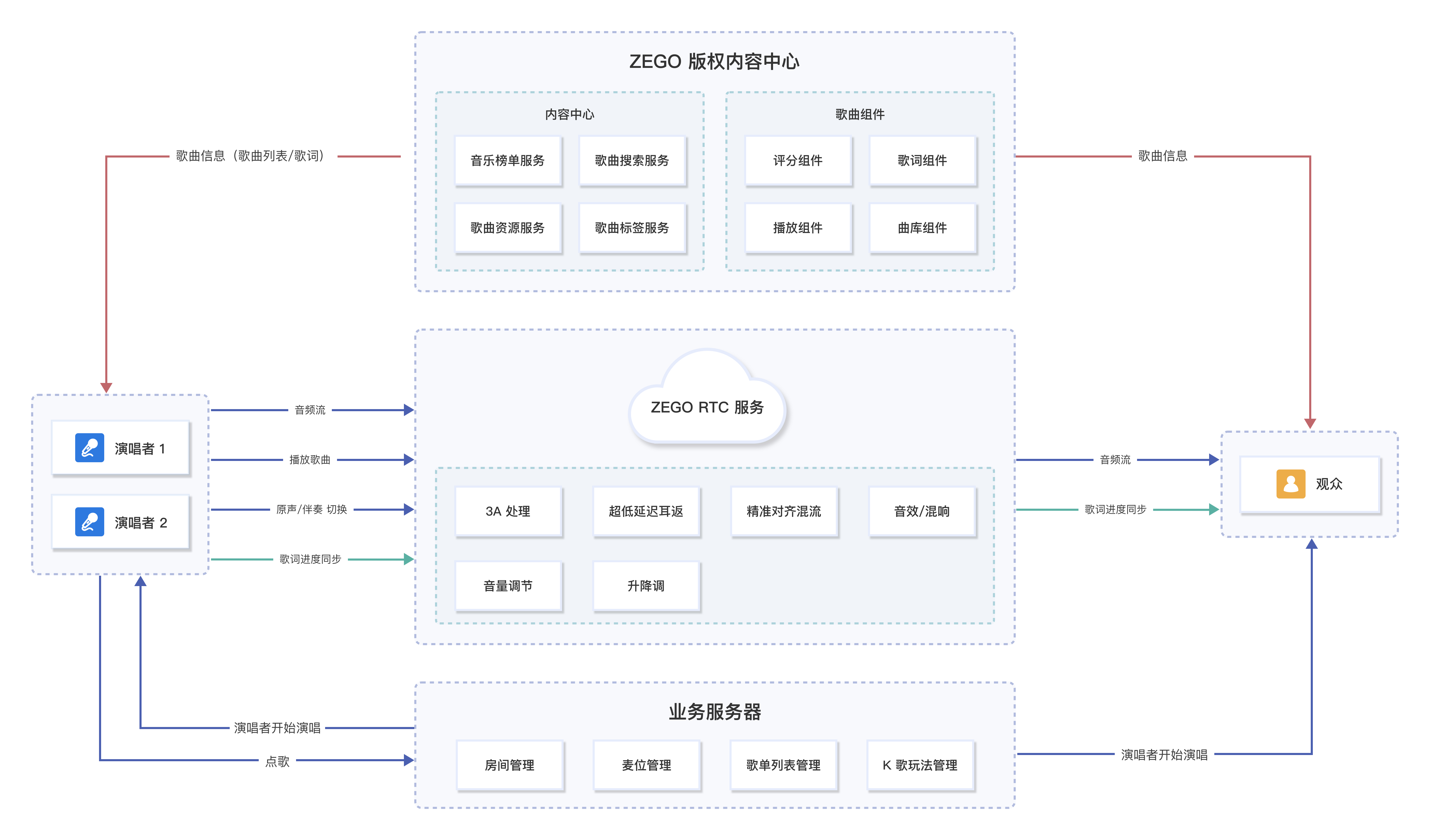
【音视频SDK测评】线上K歌软件开发技术选型
摘要 在线K歌软件的开发有许多技术难点,需考虑到音频录制和处理、实时音频传输和同步、音频压缩和解压缩、设备兼容性问题等技术难点外,此外,开发者还应关注音乐版权问题,确保开发的应用合规合法。 前言 前面写了几期关于直播 …...

Jackson:String转object反序列化失败
场景 消费mq时String转Object 代码 for (MessageExt msg : msgs) {String msgBody new String(msg.getBody(), StandardCharsets.UTF_8);BinlogEvent binlogEvent JsonUtil.silentString2Object(msgBody, BinlogEvent.class);binlogEvent.setPort(Long.valueOf(port));tCo…...

Spark_Core---6
spark 相关概念补充 课程目标 了解spark的安装部署知道spark作业提交集群的过程 6.1 spark的安装部署 1、下载spark安装包 http://spark.apache.org/downloads.html 高版本不存在cdh的编译版本,可以从官网下载源码版本,指定高版本hadoop进行编译 编译…...

游戏运营需要什么条件和准备?
游戏运营是一个复杂的过程,需要综合考虑多个因素。以下是一些游戏运营需要的条件和准备: 1、良好的游戏产品 首先,需要有一款优秀、有吸引力的游戏产品。游戏的质量和内容决定了用户是否愿意下载、留存和付费。 2、游戏运营团队 拥有专业…...

SVN限制Message提交的格式
限制Message提交的格式必须为以下格式 [Version] [Description] [TPA] [Doors] REPOS"$1" TXN"$2"# Make sure that the log message contains some text. SVNLOOK/usr/bin/svnlook MSG$SVNLOOK log -t "$TXN" "$REPOS"if [[ $MSG ~ …...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
