【动态规划】子序列系列
文章目录
- 动态规划(子序列系列)
- 1. 最长递增子序列
- 2. 摆动序列
- 3. 最长递增子序列的个数
- 4. 最长数对链
- 5. 最长定差子序列
- 6. 最长的斐波那契子序列的长度
- 7. 最长等差数列
- 8. 等差数列划分 || - 子序列
动态规划(子序列系列)
1. 最长递增子序列
题目链接
-
状态表示
dp[i]表示到 i 位置时,所有子序列当中最长的子序列的长度 -
状态转移方程
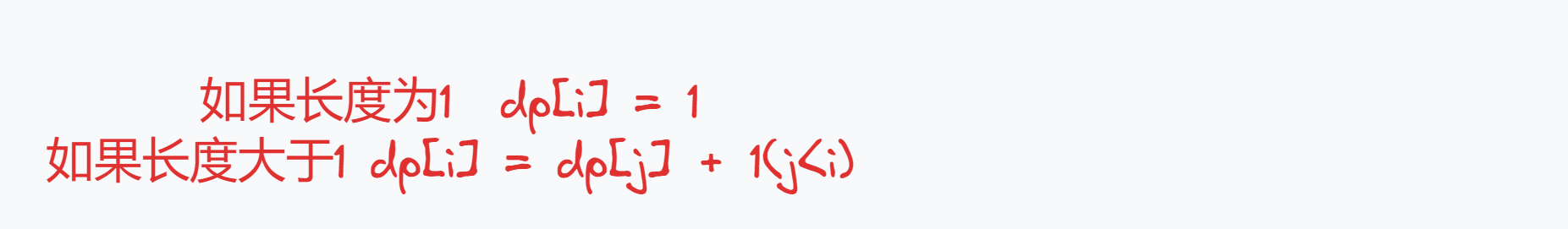
-
初始化
表中的所有数据初始化为1
-
填表
从左到右
-
返回值
返回整个dp表里面最大的值
AC代码:
class Solution
{
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1; i < n; i++){for (int j = 0; j < i; j++){if (nums[i] > nums[j]){dp[i] = max(dp[i], dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;}
};
2. 摆动序列
题目链接
-
状态表示
f[i]表示:以 i 位置为结尾的所有子序列当中,最后一个位置是上升的最长摆动序列的长度g[i]表示:以 i 位置为结尾的所有子序列当中,最后一个位置是下降的最长摆动序列的长度 -
状态转移方程
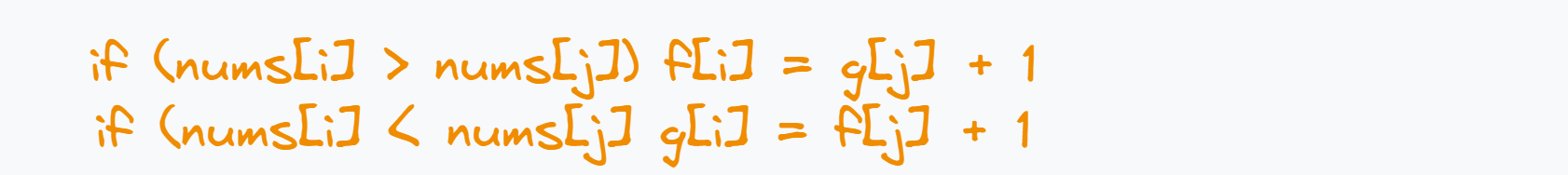
-
初始化
表中的所有值初始化为1
-
填表
从左到右
-
返回值
返回两个表中的最大值
AC代码:
class Solution
{
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();vector<int> f(n, 1), g(n, 1);int ret = 1;for (int i = 1; i < n; i++){for (int j = 0; j < i; j++){if (nums[i] > nums[j]) f[i] = max(f[i], g[j] + 1);else if (nums[i] < nums[j]) g[i] = max(g[i], f[j] + 1);}ret = max(ret, max(f[i], g[i]));}return ret;}
};
3. 最长递增子序列的个数
题目链接
这里需要用到一种思想:
如何一次遍历数组,就可以找到最大数出现的次数
代码实现:
#include <iostream>using namespace std;int main()
{int arr[] = {2, 3, 1, 234, 43, 342, 234, 5, 34, 43, 8, 342};int n = sizeof(arr)/sizeof(arr[0]);int maxval = 0;int count = 0;for (int i = 0; i < n; i++){if (arr[i] > maxval) maxval = arr[i], count = 1;else if (arr[i] == maxval) count++;}cout << maxval << endl;cout << count << endl;return 0;
}
-
状态表示
len[i]表示以 i 位置为结尾所有子序列当中,最长递增子序列的长度count[i]表示以 i 位置为结尾所有子序列当中,最长递增子序列的个数 -
状态转移方程
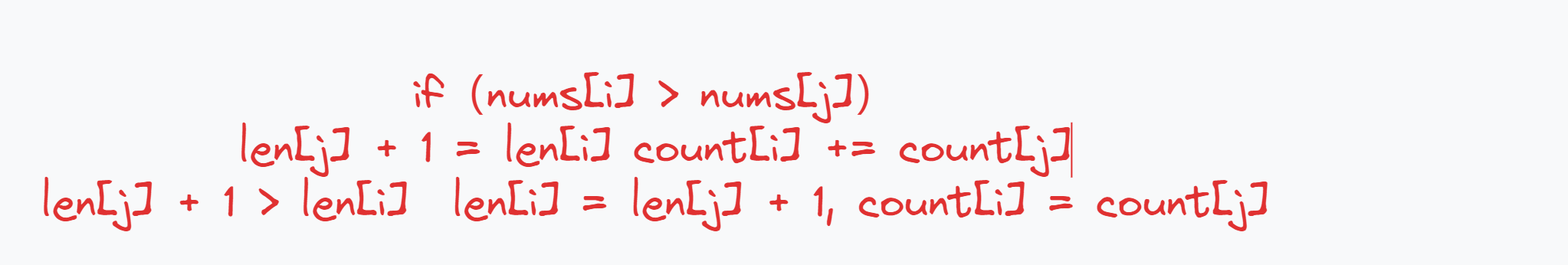
-
初始化
所有值都初始化为1
-
填表
从左到右
-
返回值
count表最后一个
AC代码:
class Solution
{
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> len(n, 1), count(n, 1);int retval = 1, retcount = 1;for (int i = 1; i < n; i++){for (int j = 0; j < i; j++){if (nums[i] > nums[j]){if (len[j] + 1 > len[i]) len[i] = len[j] + 1, count[i] = count[j];else if (len[j] + 1 == len[i]) count[i] += count[j];}}if (retval == len[i]) retcount += count[i];else if (retval < len[i]) retval = len[i], retcount = count[i];}return retcount;}
};
4. 最长数对链
题目链接
分析:状态表示以某个位置为结尾的时候,后面的元素不能影响当前的填表,但是这个题目已经影响打了,所有需要将数组排序
-
状态表示
dp[i]表示以 i 位置为结尾的所有数对链当中,最长的数对链的长度 -
状态转移方程
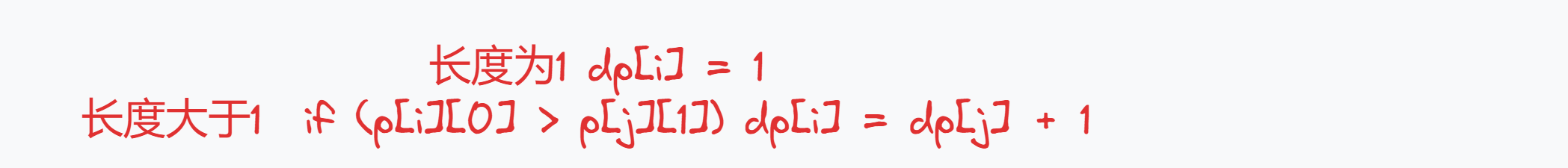
-
初始化
所有初始化为1
-
填表
从做到右
-
返回值
返回整个表的最大值
AC代码:
class Solution
{
public:int findLongestChain(vector<vector<int>>& pairs) {sort(pairs.begin(), pairs.end());int n = pairs.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1; i < n; i++){for (int j = 0; j < i; j++){if (pairs[i][0] > pairs[j][1]) {dp[i] = max(dp[i], dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;}
};
5. 最长定差子序列
题目链接
-
状态表示
dp[i]表示到 i 位置时,所有的子序列当中最长的定差子序列的长度 -
状态转移方程

-
初始化
将第一个元素对应的dp值初始化为1
-
填表
从左到右
-
返回值
返回整个dp表里的最大值
AC代码:
class Solution
{
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int, int> hash;hash[arr[0]] = 1;int ret = 1;for (int i = 1; i < arr.size(); i++){hash[arr[i]] = hash[arr[i] - difference] + 1;ret = max(ret, hash[arr[i]]);}return ret;}
};
6. 最长的斐波那契子序列的长度
题目链接
-
状态表示
dp[i][j]表示以 i j 为结尾的所有子序列当中,最长的斐波那契数列的长度 -
状态转移方程

优化:将数组的元素和下标绑定,方便查找
-
初始化
-
填表
-
返回值
返回值可能小于3, 这是应该返回0
AC代码:
class Solution
{
public:int lenLongestFibSubseq(vector<int>& arr) {int n = arr.size();unordered_map<int, int> hash;for (int i = 0; i < n; i++) hash[arr[i]] = i;vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for (int j = 2; j < n; j++) // 固定最后一个位置{for (int i = 1; i < j; i++){int a = arr[j] - arr[i];if (a < arr[i] && hash.count(a)){dp[i][j] = dp[hash[a]][i] + 1;}ret = max(ret, dp[i][j]);}}return ret < 3 ? 0 : ret;}
};
7. 最长等差数列
题目链接
-
状态表示
dp[i][j] 表示 以 i j 为结尾的所有子序列当中最长的等差子序列的长度 -
状态转移方程

优化:一边dp一边保存离它最近元素的下标,当 i 位置填完之后将它填入哈希表中即可。所以需要先固定第倒数第二个元素,接着固定倒数第一个元素
-
初始化
-
填表
-
返回值
返回是整个dp表里的最大值
AC代码:
class Solution
{
public:int longestArithSeqLength(vector<int>& nums) {unordered_map<int, int> hash;int n = nums.size();hash[nums[0]] = 0;vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for (int i = 1; i < n; i++){for (int j = i + 1; j < n; j++){int a = 2 * nums[i] - nums[j];if (hash.count(a)){dp[i][j] = dp[hash[a]][i] + 1;}ret = max(ret, dp[i][j]);}hash[nums[i]] = i;}return ret;}
};
8. 等差数列划分 || - 子序列
题目链接
-
状态表示
dp[i][j]表示以 i j 为是等差数列的子序列的个数 -
状态表示

-
初始化
-
填表
-
返回值
AC代码:
class Solution
{
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();unordered_map<long long, vector<int>> hash;for (int i = 0; i < n; i++) hash[nums[i]].push_back(i);vector<vector<int>> dp(n, vector<int>(n));int sum = 0;for (int j = 2; j < n; j++) // 固定倒数第一个{for (int i = 1; i < j; i++){long long a = (long long)nums[i] * 2 - nums[j];if (hash.count(a)){for (auto k : hash[a]){if (k < i) dp[i][j] += dp[k][i] + 1;else break;}}sum += dp[i][j];}}return sum;}
};
相关文章:

【动态规划】子序列系列
文章目录 动态规划(子序列系列)1. 最长递增子序列2. 摆动序列3. 最长递增子序列的个数4. 最长数对链5. 最长定差子序列6. 最长的斐波那契子序列的长度7. 最长等差数列8. 等差数列划分 || - 子序列 动态规划(子序列系列) 1. 最长递…...

URL存储解锁数据管理的新思路,重新定义数据传输与共享(@vue/repl)
Thinking系列,旨在利用10分钟的时间传达一种可落地的编程思想。 近日,在了解 vue/repl 相关内容,其通过 URL 进行数据存储,感觉思路惊奇,打开了新方式。 首先,通过 URL 存储最大的便利是:无需服…...

matlab程序中文乱码
不同版本的matlab共存在GBK(即,ANSI)和UTF-8两种编码方式,因此可能会出现乱码问题。 第一步:在matlab的命令行窗口输入指令,查看当前编码方式 feature(locale) 第二步:用Notepad打开文件&…...
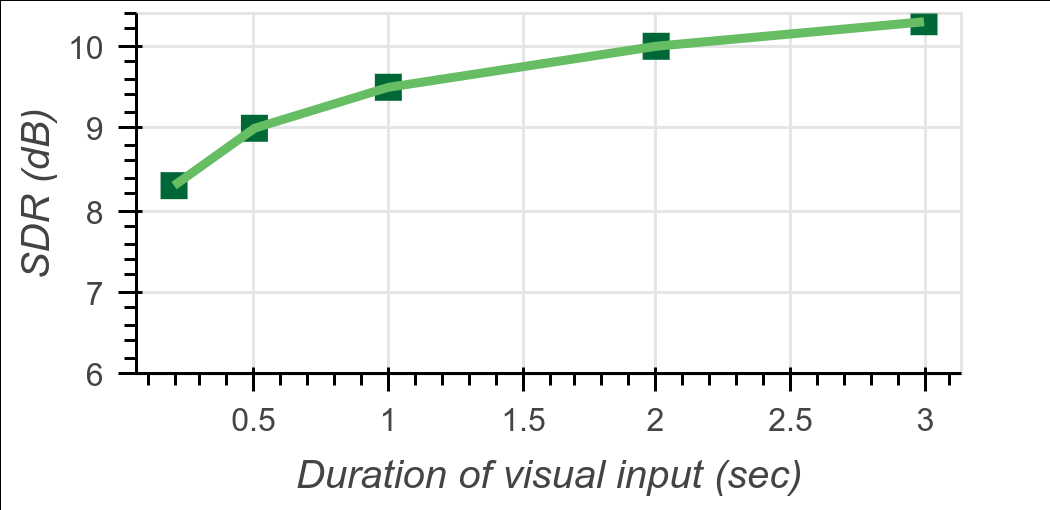
【计算机视觉|语音分离】期望在嘈杂环境中聆听:一个用于语音分离的不依赖于讲话者的“音频-视觉模型”
本系列博文为深度学习/计算机视觉论文笔记,转载请注明出处 标题:Looking to Listen at the Cocktail Party: A Speaker-Independent Audio-Visual Model for Speech Separation 链接:Looking to listen at the cocktail party: a speaker-in…...

curl 介绍和使用
文章目录 一、介绍1.1 curl 介绍1.2 curl 参数介绍1.3 类似Curl的工具和库 二、使用2.1 curl 下载2.2 curl 示例用法2.3 curl命令使用digest方式验证用户 一、介绍 1.1 curl 介绍 官网:https://curl.se/GitHub源码:https://github.com/curl/curl Curl…...

5、VMWARE安装、MobaXterm SSH连接 、Ubuntu xrdp安装使用
以下是在VMware中安装Ubuntu 22.04的详细步骤: 下载Ubuntu 22.04镜像文件: 前往Ubuntu官方网站或其他可信来源,下载Ubuntu 22.04的镜像文件(.iso格式)。 创建虚拟机: 打开VMware Workstation软件…...

Docker dockerfile 案例:centos 支持 vim
创建一个 centos 容器,容器内默认是不支持使用 vim 指令的,只能使用 vi 指令。(附:Dockerfile 语法与指令) 但想在创建 centos 容器后就支持 vim 指令,需要自定义 centos,编写 dockerfile&…...

Git忽略已经提交过一次的文件 Git忽略文件
1、从未提交过的文件可以用.gitignore 也就是添加之后从来没有提交(commit)过的文件,可以使用.gitignore忽略该文件 该文件只能作用于未跟踪的文件(Untracked Files),也就是那些从来没有被 git 记录过…...

Scala项目找不到或无法加载主类
目录 1,出错背景2,分析与解决 1,出错背景 Scala项目无法创建scale和Java文件。项目没有报错,但执行时项目总是找不到项目下的类,报错信息如下所示: 错误: 找不到或无法加载主类 com.my.memTestCheck但该类…...
八大排序算法--选择排序(动图理解)
选择排序 算法思路 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。 选择排序的步骤: 1>首先在未排序序列中找到最小(大)元素…...
6.s081(Fall 2022)Lab2: system calls
文章目录 前言其他篇章参考链接0. 前置准备1. System call tracing (moderate) 前言 好像没啥前言 其他篇章 环境搭建 Lab1:Utilities 参考链接 官网链接 xv6手册链接,这个挺重要的,建议做lab之前最好读一读。 xv6手册中文版,这是几位先…...
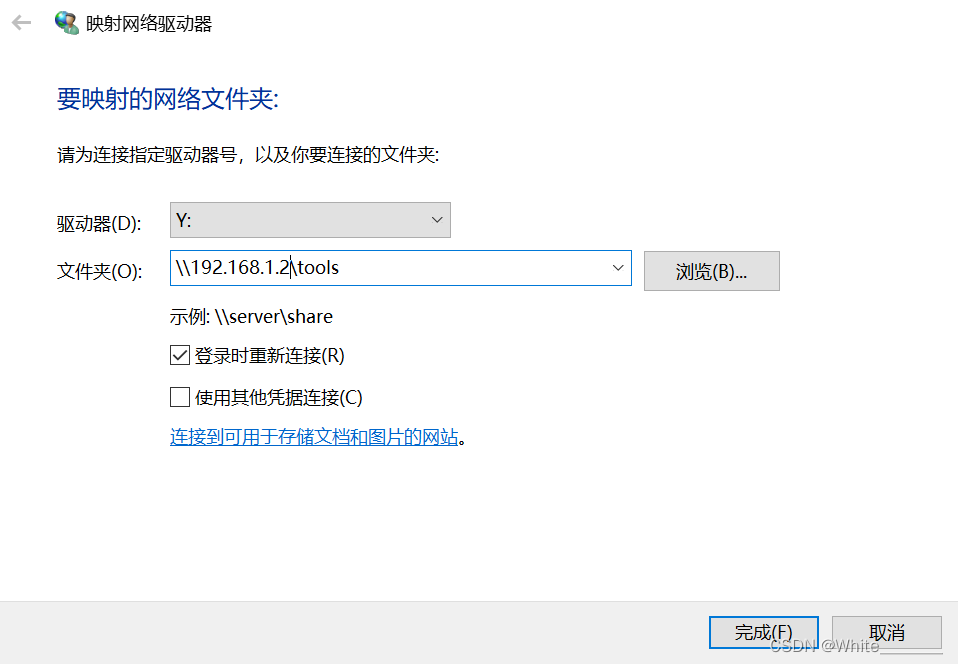
SAMBA 文件分享相关 笔记
目标说明 在Linux 安装Samba,然后在Windows端映射为网络硬盘 流程 Linux 端命令 apt install samba -y 默认情况下软件会询问是否迁移系统网络设置以搭建协议,选择迁移即可修改配置文件 vim /etc/samba/smb.conf Samba 的配置文件中会带一个名为 prin…...
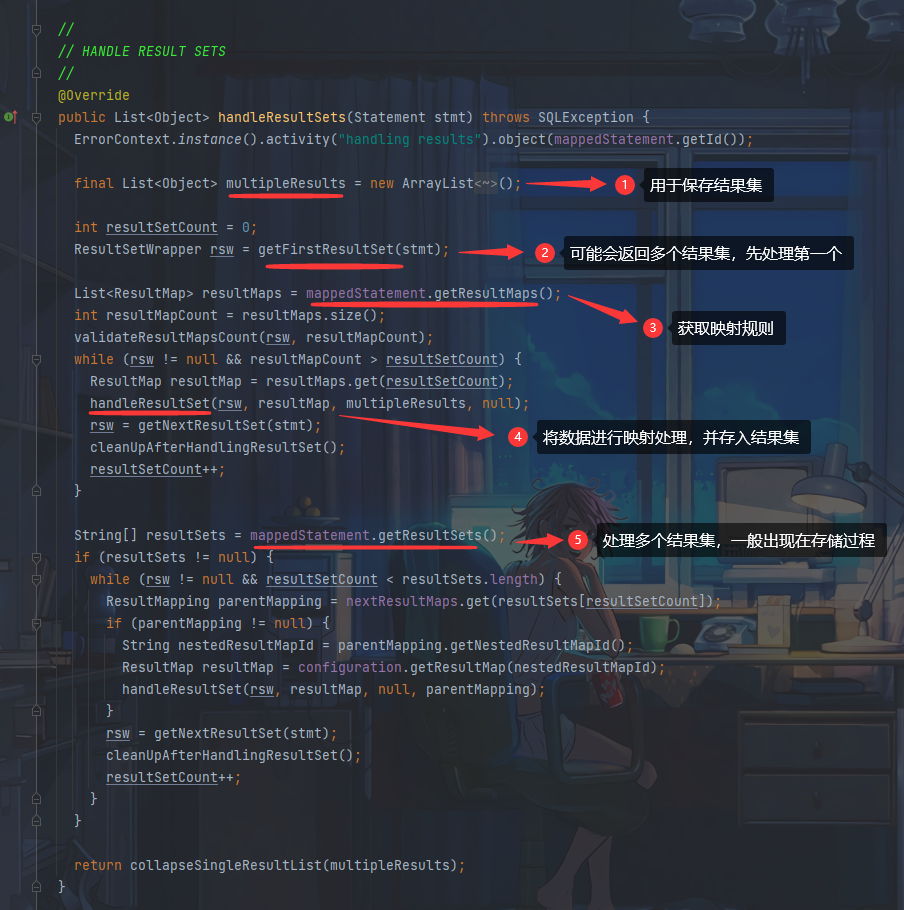
Mr. Cappuccino的第53杯咖啡——Mybatis源码分析
Mybatis源码分析 Mybatis源码分析入口1. 读取配置文件总结 2. 解析配置文件核心代码(一)核心代码(二)分析parse()方法分析build()方法 总结 3. 获取SqlSession总结 4. 获取mapper代理对象总结 5. 使用mapper代理对象执行Sql语句二…...
修改文件格式(查看文件拓展名)
很多时候我们直接把txt文件重命名为xxx.c或者别的文件格式,文件类型依然会是txt,文件名并不会变成我们想要的xxx.c,而是xxx.c.txt,也就是下面这个样子 给大家介绍2种方法去解决这个问题 目录 1.另存为新格式 2.显示文件拓展名 1…...

利用鸿鹄可观测性监控Istio Ingress网关
一、需求描述 在上一篇《利用Vector和鸿鹄搭建微服务应用的可观测性平台》中,阐述了微服务的基本概念、优点及如何利用鸿鹄来处理分布式应用的日志。本文将进一步讨论微服务架构面临的问题、服务网格及鸿鹄处理Istio Gateway的独特优势。 1.1 微服务架构面临的挑战 …...
vscode 前端开发插件 2023
自己记录 安装vscode后必装插件 chinesegit 必装没啥可说 随时更新 1.CSS Navigation CTRL点击类名可跳转到对应样式位置。 如果是scss less的话。css peak插件无法生效 2.GitLens — Git supercharged 可以看到每一行的git提交记录。 3.Auto Rename Tag 可以同步更新…...
使用docker部署Wordpress
文章目录 1.创建网络2.创建volume存储3.拉取镜像4.创建mysql容器mysql修改密码 5.创建wordpress容器6.访问localhost:80就可以直接使用啦 1.创建网络 docker network create --subnet172.18.0.0/24 pro-net2.创建volume存储 # mysql 存储 docker volume create volume_mysql…...

7.31黄金最新行情走势分析及多空交易策略
近期有哪些消息面影响黄金走势?黄金多空该如何研判? 黄金消息面解析:上周有重磅数据美联储加息的消息,黄金受其影响波动比较频繁,总体空间40美金。但这个过程跌宕起伏。收线来看黄金在连续上涨三周后迎来一根小阴十…...

Spring框架——AOP注解方式
目录 Spring框架的AOP技术(注解方式) 通知类型 Spring框架的AOP技术(注解方式) 1. 步骤一:创建JavaWEB项目,引入具体的开发的jar包* 先引入Spring框架开发的基本开发包com.springsource.org.apache.commo…...

Java 日志(Logging)如何创建和捕获日志消息和文件
Java允许我们通过日志记录过程来创建和捕获日志消息和文件。 在Java中,日志记录需要框架和API。Java在java.util.logging程序包中具有内置的日志记录框架。 Java 日志组件 下图显示了Java Logging API(java.util.logging)的核心组件和指定…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
