【Windows】磁盘快捷修复
【Windows】磁盘快捷修复
- 1、背景
- 2、关于Chkdsk
- 3、示例
1、背景
前段时间使用U盘拷贝文件过程中,突然发现U盘无法读取了,U盘里面存储的数据也无法获取。
然后使用windows系统的chkdsk命令进行修复。
chkdsk全称:checkdisk,即磁盘检查!
调用chkdsk命令行来检查某一个磁盘分区。
chkdsk工具基于被检测的分区所用的文件系统,创建和显示磁盘的状态报告。
当 "chkdsk 磁盘 " 如果不带任何参数,chkdsk 将显示当前驱动器中的磁盘状态。
后边的/f就是修复命令,即列出并纠正磁盘上的错误。
注意: /f 参数时,如果关机会中断 chkdsk 进程,可能会导致磁盘出现完整性错误!
2、关于Chkdsk
Chkdsk对应的是Chkdsk.exe,在windows系统目录:C:\Windows\System32
Chkdsk.exe 程序用于验证文件系统的逻辑完整性。
如果 CHKDSK 在文件系统数据中发现存在逻辑不一致性,指定参数 /f 将执行可修复该文件系统数据的操作(非只读模式)。
语法:
chkdsk [volume:] [[Path] FileName] [/f] [/v] [/r] [/x] [/c] [/l[:size]]
| 参数 | 说明 |
|---|---|
| volume: | 指定驱动器号(冒号分隔)、装入点或卷名。 |
| [Path} FileName] | 指定 chkdsk 检查碎片整理的文件或文件集的位置和名称。使用通配符(* 和 ?)可以指定多个文件。 |
| /f | 修复磁盘上的错误。必须锁定磁盘。 |
| /v | 当检查磁盘时,显示所有目录中每个文件的名称。 |
| /r | 找到坏扇区并恢复可读取的信息。必须锁定磁盘。 |
注意以上字母不区分大小写!
3、示例
使用参数 /r 来恢复扇区!如下:
C:\Users\Administrator>chkdsk G: /R
文件系统的类型是 NTFS。
卷标是 Ventoy。阶段 1: 检查基本文件系统结构...
删除损坏的文件记录段 1A。
删除损坏的文件记录段 2C3。
删除损坏的文件记录段 2D3。已处理 2560 个文件记录。
文件验证完成。阶段持续时间 (文件记录验证): 169.52 毫秒。
删除孤立文件记录段 25。
删除孤立文件记录段 2A6。已处理 3 个大型文件记录。
删除孤立文件记录段 2D5。阶段持续时间 (孤立文件记录恢复): 0.00 毫秒。已处理 0 个错误的文件记录。阶段持续时间 (文件记录检查错误): 7.46 毫秒。阶段 2: 检查文件名链接...
正在修复文件记录段 5 中的错误信息。
正在修复文件记录段 B 中的错误信息。已处理 2564 个索引项。
索引验证完成。阶段持续时间 (索引验证): 82.95 毫秒。
CHKDSK 正在创建新的根目录。
CHKDSK 正在扫描未编制索引的文件以便重新连接到其原始目录。
正在将孤立文件 $MFT (0)恢复到目录文件 5。
正在将孤立文件 $MFTMirr (1)恢复到目录文件 5。
正在将孤立文件 $LogFile (2)恢复到目录文件 5。
正在将孤立文件 $Volume (3)恢复到目录文件 5。
正在将孤立文件 $AttrDef (4)恢复到目录文件 5。
正在修复文件记录段 5 中的错误信息。
正在将孤立文件 . (5)恢复到目录文件 5。
正在将孤立文件 $Bitmap (6)恢复到目录文件 5。
正在将孤立文件 $Boot (7)恢复到目录文件 5。
正在将孤立文件 $BadClus (8)恢复到目录文件 5。
正在将孤立文件 $Secure (9)恢复到目录文件 5。
正在跳过有关恢复孤立项的进一步消息。已扫描到 373 个未索引文件。已将 14 个未编制索引的文件恢复到原始目录。阶段持续时间 (孤立文件重新连接): 0.00 毫秒。
CHKDSK 正在恢复剩余的未索引文件。已将 359 个未编制索引的文件恢复到回收箱。回收箱位于 \found.000阶段持续时间 (孤立文件恢复到回收箱): 0.00 毫秒。
正创建文件 B 的索引 $I30。
正创建对象 ID 文件。
正在将索引项插入文件 B 的索引 $I30 中。
正创建文件 13 的索引 $O。
正在将索引项插入文件 13 的索引 $O 中。已处理 2 个重新解析记录。
正在将索引项插入文件 13 的索引 $O 中。
正在创建重新分析点文件。
正在将索引项插入文件 B 的索引 $I30 中。
正创建文件 14 的索引 $R。阶段持续时间 (重分析点和对象 ID 验证): 53.68 毫秒。
正创建配额文件。
正在将索引项插入文件 B 的索引 $I30 中。
正创建文件 15 的索引 $O。
正创建文件 15 的索引 $Q。
在文件 15 的索引 $Q 中插入默认配额记录。阶段 3: 检查安全描述符...
正创建文件 9 的索引 $SII。
正创建文件 9 的索引 $SDH。
使用文件 3 的默认安全 ID 替换无效的安全 ID。
使用文件 3D 的默认安全 ID 替换无效的安全 ID。
使用文件 60 的默认安全 ID 替换无效的安全 ID。
为未定义的安全 ID 100 创建默认安全描述符。
为未定义的安全 ID 109 创建默认安全描述符。
安全描述符验证完成。阶段持续时间 (安全描述符验证): 0.92 毫秒。
正在文件 4 中插入数据属性。
正在文件 6 中插入数据属性。
正在文件 7 中插入数据属性。
正在文件 8 中插入数据属性。
正在文件 A 中插入数据属性。已处理 7 个数据文件。阶段持续时间 (数据属性验证): 14.02 毫秒。阶段 4: 在用户文件数据中查找损坏的群集...已处理 2544 个文件。
文件数据验证完成。阶段持续时间 (用户文件恢复): 1.67 分钟。阶段 5: 查找损坏的空闲群集...已处理 3353380 个可用簇。
已完成可用空间验证。阶段持续时间 (可用空间恢复): 0.00 毫秒。
正在更正主文件表(MFT)镜像的错误。
正在修复属性定义表的错误。
正在更正启动文件的错误。
正在修正大写文件中的错误。
正在修复不正确的群集文件的错误。
CHKDSK 正在重置恢复信息...
CHKDSK 正在重置日志文件。
正在更正主文件表(MFT) BITMAP 属性的错误。
正在更正卷位图的错误。Windows 已更正文件系统。
无需采取进一步操作。总共有 15154175 KB 磁盘空间。
375 个文件中有 1715180 KB。
12 个索引 104 KB。
坏扇区 0 KB。
系统正在使用 25963 KB。
日志文件占用了 22528 KB。
磁盘上 13412928 KB 可用。每个分配单元中有 4096 字节。
磁盘上共有 3788543 个分配单元。
磁盘上有 3353232 个可用的分配单元。
总持续时间: 1.87 分钟 (112639 毫秒)。
注意:
实际使用恢复能恢复一部分,很难全部恢复丢失的数据。
实际硬盘上丢失数据通过该命令也难以全部找回数据!
相关文章:

【Windows】磁盘快捷修复
【Windows】磁盘快捷修复 1、背景2、关于Chkdsk3、示例 1、背景 前段时间使用U盘拷贝文件过程中,突然发现U盘无法读取了,U盘里面存储的数据也无法获取。 然后使用windows系统的chkdsk命令进行修复。 chkdsk全称:checkdisk,即磁盘…...
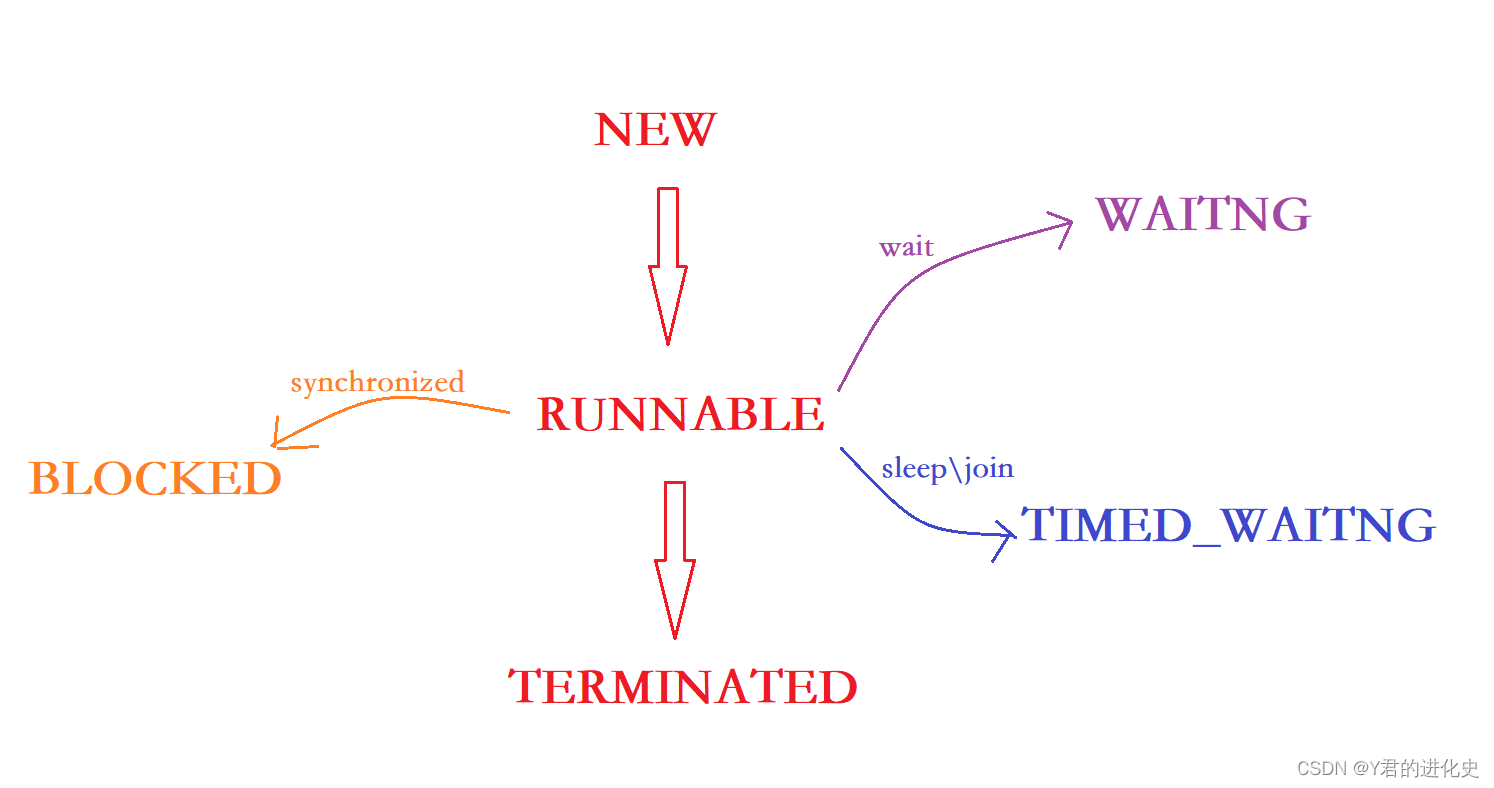
Java 线程的多种状态
前言 在前文中详细介绍了线程的启动、中断、休眠、等待。本文详细介绍线程的多种状态。 获取线程的当前状态代码是: 线程对象.getState(); 目录 前言 一、NEW 二、RUNNABLE 三、BLOCKED 四、WAITNG 五、TIMED_WAITNG 六、TERMINATED 结语 一、NEW Thread 对…...

AI绘画| 迪士尼风格|可爱头像【附Midjourney提示词】
Midjourney案例分享 图片预览 迪士尼风格|可爱头像 高清原图及关键词Prompt已经放在文末网盘,需要的自取 在数字艺术的新时代,人工智能绘画已经迅速崭露头角。作为最先进的技术之一,AI绘画结合了艺术和科学,开启了一…...

【浪费了我两个小时时间】Microsoft store无法加载页面0x80131500
绕的圈,踩的坑 谷歌搜索, newbing搜索都叫我清理缓存,重新安装等方法。 还被这篇文章误导了一下:微软应用商店错误代码0x80072EFD怎么办?(已解决) 加上重启电脑各种试不行。 最后想到要去改代…...

【动态规划】子序列系列
文章目录 动态规划(子序列系列)1. 最长递增子序列2. 摆动序列3. 最长递增子序列的个数4. 最长数对链5. 最长定差子序列6. 最长的斐波那契子序列的长度7. 最长等差数列8. 等差数列划分 || - 子序列 动态规划(子序列系列) 1. 最长递…...

URL存储解锁数据管理的新思路,重新定义数据传输与共享(@vue/repl)
Thinking系列,旨在利用10分钟的时间传达一种可落地的编程思想。 近日,在了解 vue/repl 相关内容,其通过 URL 进行数据存储,感觉思路惊奇,打开了新方式。 首先,通过 URL 存储最大的便利是:无需服…...

matlab程序中文乱码
不同版本的matlab共存在GBK(即,ANSI)和UTF-8两种编码方式,因此可能会出现乱码问题。 第一步:在matlab的命令行窗口输入指令,查看当前编码方式 feature(locale) 第二步:用Notepad打开文件&…...
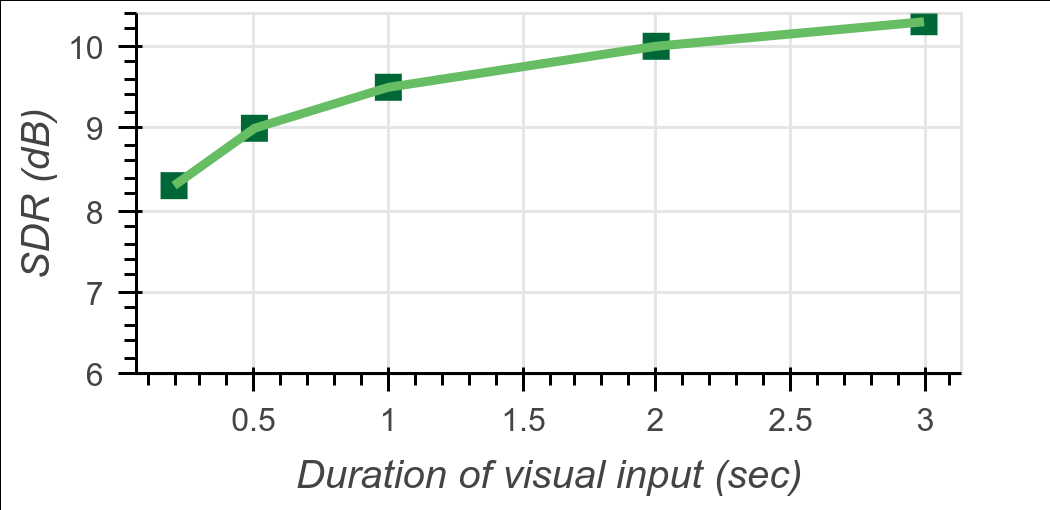
【计算机视觉|语音分离】期望在嘈杂环境中聆听:一个用于语音分离的不依赖于讲话者的“音频-视觉模型”
本系列博文为深度学习/计算机视觉论文笔记,转载请注明出处 标题:Looking to Listen at the Cocktail Party: A Speaker-Independent Audio-Visual Model for Speech Separation 链接:Looking to listen at the cocktail party: a speaker-in…...

curl 介绍和使用
文章目录 一、介绍1.1 curl 介绍1.2 curl 参数介绍1.3 类似Curl的工具和库 二、使用2.1 curl 下载2.2 curl 示例用法2.3 curl命令使用digest方式验证用户 一、介绍 1.1 curl 介绍 官网:https://curl.se/GitHub源码:https://github.com/curl/curl Curl…...

5、VMWARE安装、MobaXterm SSH连接 、Ubuntu xrdp安装使用
以下是在VMware中安装Ubuntu 22.04的详细步骤: 下载Ubuntu 22.04镜像文件: 前往Ubuntu官方网站或其他可信来源,下载Ubuntu 22.04的镜像文件(.iso格式)。 创建虚拟机: 打开VMware Workstation软件…...

Docker dockerfile 案例:centos 支持 vim
创建一个 centos 容器,容器内默认是不支持使用 vim 指令的,只能使用 vi 指令。(附:Dockerfile 语法与指令) 但想在创建 centos 容器后就支持 vim 指令,需要自定义 centos,编写 dockerfile&…...

Git忽略已经提交过一次的文件 Git忽略文件
1、从未提交过的文件可以用.gitignore 也就是添加之后从来没有提交(commit)过的文件,可以使用.gitignore忽略该文件 该文件只能作用于未跟踪的文件(Untracked Files),也就是那些从来没有被 git 记录过…...

Scala项目找不到或无法加载主类
目录 1,出错背景2,分析与解决 1,出错背景 Scala项目无法创建scale和Java文件。项目没有报错,但执行时项目总是找不到项目下的类,报错信息如下所示: 错误: 找不到或无法加载主类 com.my.memTestCheck但该类…...
八大排序算法--选择排序(动图理解)
选择排序 算法思路 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。 选择排序的步骤: 1>首先在未排序序列中找到最小(大)元素…...
6.s081(Fall 2022)Lab2: system calls
文章目录 前言其他篇章参考链接0. 前置准备1. System call tracing (moderate) 前言 好像没啥前言 其他篇章 环境搭建 Lab1:Utilities 参考链接 官网链接 xv6手册链接,这个挺重要的,建议做lab之前最好读一读。 xv6手册中文版,这是几位先…...
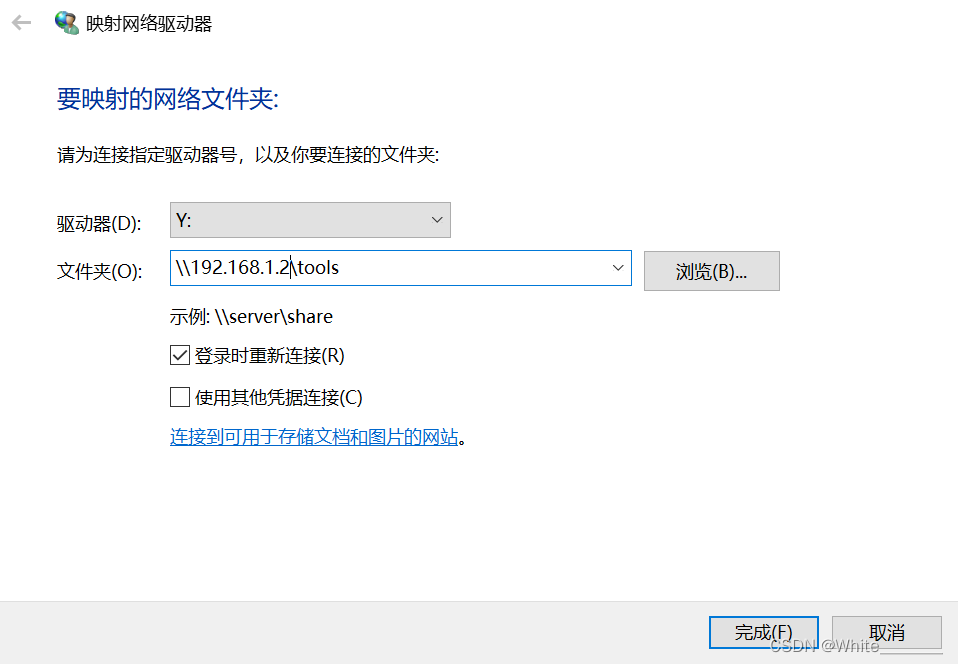
SAMBA 文件分享相关 笔记
目标说明 在Linux 安装Samba,然后在Windows端映射为网络硬盘 流程 Linux 端命令 apt install samba -y 默认情况下软件会询问是否迁移系统网络设置以搭建协议,选择迁移即可修改配置文件 vim /etc/samba/smb.conf Samba 的配置文件中会带一个名为 prin…...
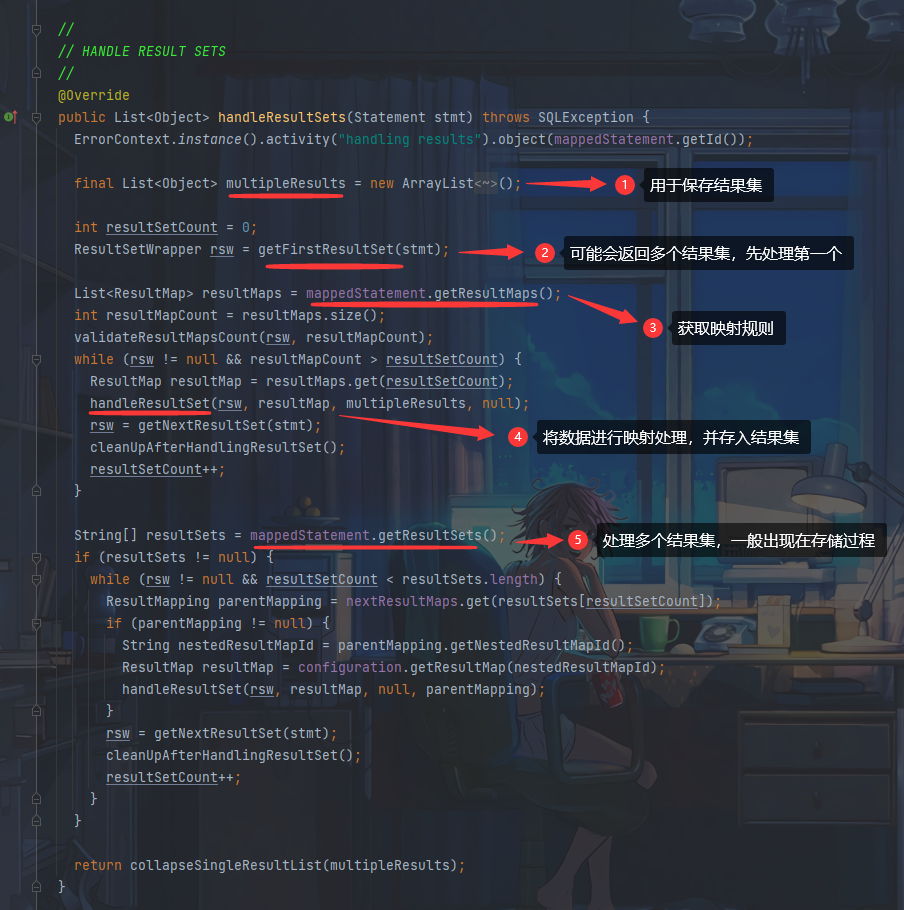
Mr. Cappuccino的第53杯咖啡——Mybatis源码分析
Mybatis源码分析 Mybatis源码分析入口1. 读取配置文件总结 2. 解析配置文件核心代码(一)核心代码(二)分析parse()方法分析build()方法 总结 3. 获取SqlSession总结 4. 获取mapper代理对象总结 5. 使用mapper代理对象执行Sql语句二…...
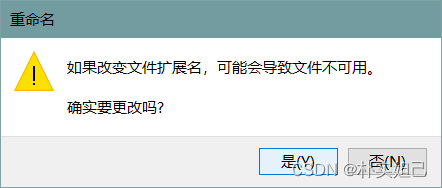
修改文件格式(查看文件拓展名)
很多时候我们直接把txt文件重命名为xxx.c或者别的文件格式,文件类型依然会是txt,文件名并不会变成我们想要的xxx.c,而是xxx.c.txt,也就是下面这个样子 给大家介绍2种方法去解决这个问题 目录 1.另存为新格式 2.显示文件拓展名 1…...

利用鸿鹄可观测性监控Istio Ingress网关
一、需求描述 在上一篇《利用Vector和鸿鹄搭建微服务应用的可观测性平台》中,阐述了微服务的基本概念、优点及如何利用鸿鹄来处理分布式应用的日志。本文将进一步讨论微服务架构面临的问题、服务网格及鸿鹄处理Istio Gateway的独特优势。 1.1 微服务架构面临的挑战 …...
vscode 前端开发插件 2023
自己记录 安装vscode后必装插件 chinesegit 必装没啥可说 随时更新 1.CSS Navigation CTRL点击类名可跳转到对应样式位置。 如果是scss less的话。css peak插件无法生效 2.GitLens — Git supercharged 可以看到每一行的git提交记录。 3.Auto Rename Tag 可以同步更新…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
uni-app学习笔记二十七--设置底部菜单TabBar的样式
官方文档地址:uni.setTabBarItem(OBJECT) | uni-app官网 uni.setTabBarItem(OBJECT) 动态设置 tabBar 某一项的内容,通常写在项目的App.vue的onLaunch方法中,用于项目启动时立即执行 重要参数: indexnumber是tabBar 的哪一项&…...
