LinearAlgebraMIT_6_ColumnSpaceAndNullSpace
这节课的两个重点是column space列空间和null space零空间。
x.1 pre-multiply/left multiply and post-multiply/right multiply
对于pre-multiply/left multiply左乘和post-multiply/right multiply右乘,如果用英文的pre-和post-是比较容易理解的, A B AB AB的意思是: A A A左乘(于) B B B或者 B B B右乘(于) A A A。
x.2 Linear Combination
linear combination线性组合是线性代数的核心,我们以举例子的方式来讲解线性组合,假设我们有一个4行3列的矩阵,我们将矩阵列分成3个向量构成的向量组 [ α 1 , α 2 , α 3 ] [\alpha_1, \alpha_2, \alpha_3] [α1,α2,α3],用这个向量组左乘于一个3*1的列向量,则是由列向量构成的向量组的线性组合。

同理,将矩阵A行分后便是行向量的线性组合。
x.3 Vector Space and Subspace
我们首先回忆一下上节课的内容,上节课的重点内容是vector space向量空间和subspace子空间。向量空间的定义是,对于数乘和相加都是封闭的空间,即空间中的任一向量的相加或者数乘后的结果都还在向量空间中,值得注意的一点是,向量空间中一定包含零点。向量空间还有一种定义是从线性组合的角度来阐述的,即对于向量空间中任一向量的线性组合仍然在该空间中。如R3就是向量空间。

已知向量空间后,我们再引入子空间的概念,子空间是向量空间的子集,子空间的定义是子空间中的任一向量的数乘和相加都在子空间中,且注意子空间一定有零点。例如,R3的子空间就有过零点的平面和过零点的直线组成的向量。
对于两个子空间,我们还得知道两个关于子空间的性质,我们任取两个子空间P和L,他们的并集不构成子空间,但是他们的交集构成子空间。因为两个子空间相交后,可能并不是所有向量的相加操作都在子空间中,例如一条过零点的直线(且直线不在平面上)和一个过零点的平面,他们两个的并集就不构成子空间。

x.4 Column Space and Null Space
Column Space列空间和Null Space零空间是两种特殊的子空间。为了方便理解我们引入A为3*4矩阵的例子。假设A矩阵如下,
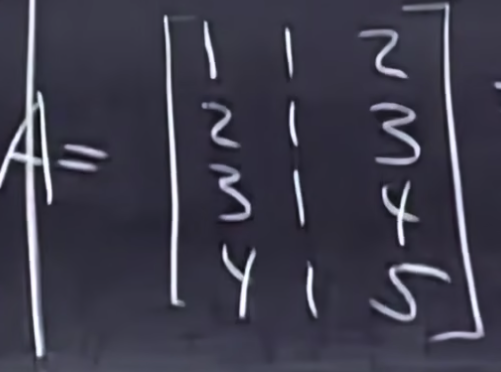
我们将A矩阵列分得到向量组 [ 1 , 2 , 3 , 4 ] , [ 1 , 1 , 1 , 1 ] , [ 2 , 3 , 4 , 5 ] [1, 2, 3, 4], [1, 1, 1, 1], [2, 3, 4, 5] [1,2,3,4],[1,1,1,1],[2,3,4,5],显而易见这是R4的向量组成的向量组,且单单这三个向量并不能构成向量空间或者子空间,我们现在想做的是,找到由这三个向量所有的线性组合组构成的向量子空间。而由前面的知识我们知道,线性组合的问题和解线性方程组的问题是一样的,我们将上面的意思翻译一下,也可以理解成是解一个Ax=b的非齐次线性方程组,而我们要做的是找到一个向量子空间,这个子空间包含所有的向量[b1, b2, b3, b4]。[x1, x2, x3]是线性组合的系数,这里我们只关注系数b,所有的系数b便构成了列空间。
首先我们需要注意,Ax=b并不一定一直有解,因为我们有四个方程(即四个约束条件),但有三个未知数(即三个自由量)。关于如何公式化求解列空间,我们将以后进行讲解,我们这里使用观察法求解。我们观察矩阵A的列分向量,我们发现有两个independent vector线性无关向量,例如我们只取第一列和第二列的列向量,而第三列的列向量可以用前面两个列向量线性表示。于是,我们用两个R4的向量的所有的线性组合便能构成列空间,列空间便被我们找到了。

我们对系数b构成的子空间——列空间研究完了,我们同时也会对解[x1, x2, x3]构成的子空间感兴趣,而对于解的子空间的研究,便是对Ax=0齐次线性方程组的研究,所有的解x便构成了零空间。我们同样使用观察法进行研究,易见[x1, x2, x3]取[0, 0, 0]方程组有解,而我们取c[1, 1, -1]也有解,于是我们找到了零空间,便是[1, 1, -1]的所有的线性组合。注意,这是R3的向量子空间,而上面那个是R4的向量子空间。

相关文章:

LinearAlgebraMIT_6_ColumnSpaceAndNullSpace
这节课的两个重点是column space列空间和null space零空间。 x.1 pre-multiply/left multiply and post-multiply/right multiply 对于pre-multiply/left multiply左乘和post-multiply/right multiply右乘,如果用英文的pre-和post-是比较容易理解的, A…...

出版物经营许可办理 出版物许可地址变更 出版物零售延期
一、出版物零售单位设立所需材料 1、申请书 2、营业执照 3、租赁合同 4、主要负责人身 份证 5、出版物经营许可申请表 二、办理出版物经营许可证所要符合的条件 1、有确定的企业名称和经营范围; 2、有出版物业务的经营场地; 3、有出版物业务的组织机构和发行人员。 三、…...
【LeetCode每日一题】——807.保持城市天际线
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 矩阵 二【题目难度】 中等 三【题目编号】 1572.矩阵对角线元素的和 四【题目描述】 给你一…...
对象)
JavaScript--Date(日期)对象
介绍和说明 创建一个Date对象并获取当前日期和时间: 使用new Date()语句可以创建一个表示当前日期和时间的Date对象。它将使用客户端设备上的当前日期和时间。例如:const currentDate new Date(); 获取特定日期的年、月、日、小时、分钟、秒࿱…...
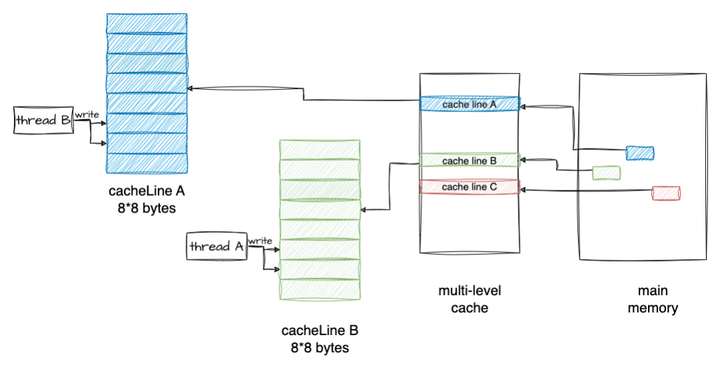
一文讲清多线程与多线程同步
1 多线程 1.1 线程的概念 十多年前,主流观点主张在可能的情况下优先选择多进程而非多线程,如今,多线程编程已经成为编程领域的事实标准。多线程技术在很大程度上改善了程序的性能和响应能力,使其能够更加高效地利用系统资源&…...

《Java-SE-第二十六章》之线程池
前言 在你立足处深挖下去,就会有泉水涌出!别管蒙昧者们叫嚷:“下边永远是地狱!” 博客主页:KC老衲爱尼姑的博客主页 博主的github,平常所写代码皆在于此 共勉:talk is cheap, show me the code 作者是爪哇岛的新手,水平很有限&…...
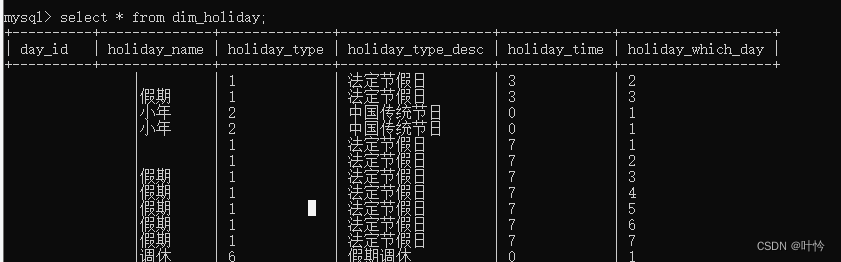
【数据库】将excel数据导入mysql数据库
环境:Windows10 mysql8以上 将你要导入的excel表另存为txt格式 打开txt格式文件,删除表头行并另存为并更改编码方式(由于与数据库的编码不同,会导致导入报错) 通过命令行登录数据库 winr cmd进入 进入装mysql的目录位…...

无涯教程-Lua - repeat...until 语句函数
与 for 和 while 循环(它们在循环顶部测试循环条件)不同,Lua编程中的 repeat ... until 循环语言在循环的底部检查其条件。 repeat ... until 循环与while循环相似,不同之处在于,保证do ... while循环至少执行一次。 repeat...until loop - …...

环形链表 LeetCode热题100
题目 给你一个链表的头节点 head ,判断链表中是否有环。 思路 快慢指针。开始快指针在慢指针前面,当快指针等于慢指针时说明有环,如果快指针指向null时说明无环。 代码 /*** Definition for singly-linked list.* struct ListNode {* …...

使用python将每组两行数据合并一行
1、使用场景 将有规律的每组(一组2行)的单数行和双数行合并为一行,以空格分割。 比如使用pssh批量得出的结果,想让ip行和结果行合并为一行(前提如上所述) [rootk8s-master1 tmp]# pssh -h iplist -i hostname [1] 18:12:42 [SU…...
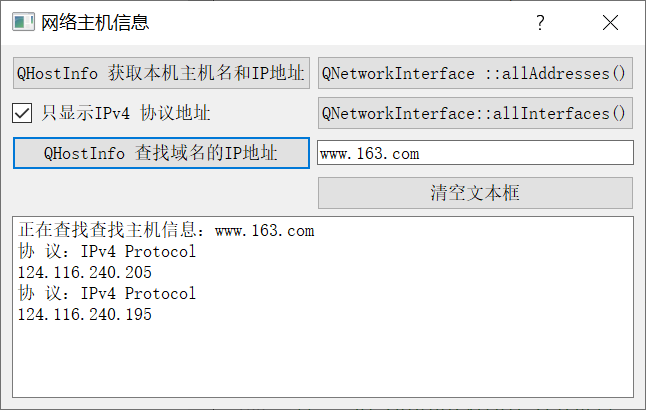
14-1_Qt 5.9 C++开发指南_网络编程及主机信息查询_HostInfo
Qt 网络模块提供了用于编写 TCP/IP 客户端和服务器端程序的各种类,如用于 TCP 通信的QTcpSocket 和 QTcpServer,用于 UDP 通信的 QUdpSocket,还有用于实现 HTTP、FTP 等普通网络协议的高级类如 QNetworkRequest,QNetworkReply 和Q…...
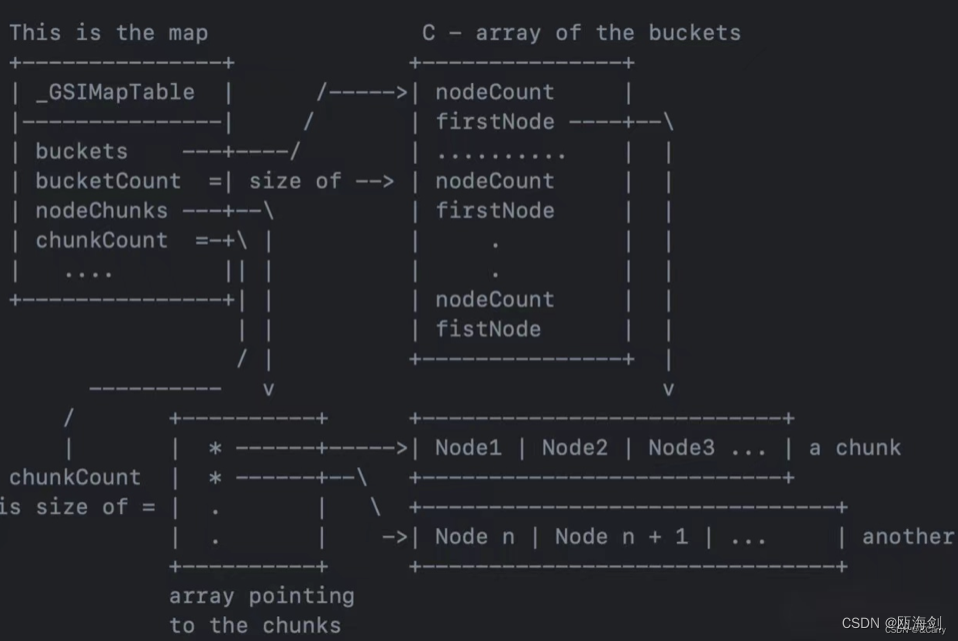
【iOS】通知原理
我们可以通过看通知的实现机制来了解通知中心是怎么实现对观察者的引用的。由于苹果对Foundation源码是不开源的,我们具体就参考一下GNUStep的源码实现。GNUStep的源码地址为:GNUStep源码GitHub下载地址, 具体源码可以进行查看。 通知的主要流程 通知全…...
创建邮件服务器(小微企业)
这里写自定义目录标题 目的硬件选型:软件选型:coremail (商业版本)postfixumail免费开源版本新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适…...
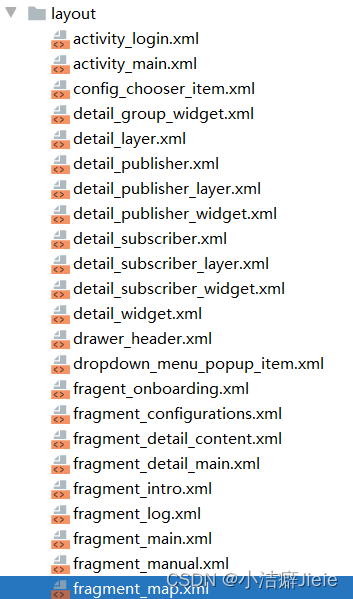
android app控制ros机器人四(调整界面布局)
半吊子改安卓,记录页面布局调整: 在ros-mobile基础上顶端增加一行,用于显示app名称和logo图像;修改标签页。 添加文字简单,但是替换图标长知识了,开始只是简单的把mipmap各个文件夹下的图片进行替换&…...
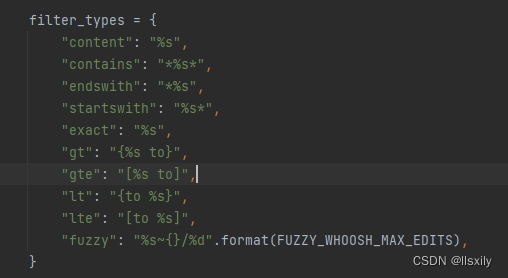
稍微深度踩坑haystack + whoosh + jieba
说到django的全文检索,网上基本推荐的都是 haystack whoosh jieba 的方案。 由于我的需求对搜索时间敏感度较低,但是要求不能有数据的错漏。 但是没有调试的情况下,搜索质量真的很差,搞得我都想直接用Like搜索数据库算了。 但是…...

微信小程序(van-tabs) 去除横向滚动条样式(附加源码解决方案+报错图)
问题描述 今天第一次接触vant组件库。 ant官网地址适用于Vue3 支持Vue2、Vue3、微信小程序等 我在使用van-tabs组件时遇到了一个问题,如下图所示: 从图片上可以看到有个灰色的横向滚动条,一开始领导给我说这个问题,我反反复复都…...

激光切割机所发出的辐射是否会对人体产生危害呢
激光切割设备所发出的激光作为一种特殊的能量光源,在一定程度上是存在辐射的。由于光纤激光器的功率通常大于半导体激光器,因此其辐射安全性也受到我们的关注。那么这种辐射的危害究竟有多大呢? 第一级:在正常操作下,不会发出对人…...
Redis 高可用:主从复制、哨兵模式、集群模式
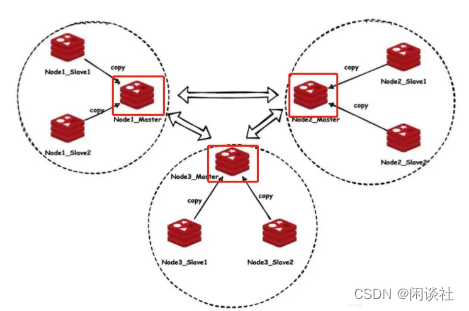
文章目录 一、redis高可用性概述二、主从复制2.1 主从复制2.2 数据同步的方式2.2.1 全量数据同步2.2.2 增量数据同步 2.3 实现原理2.3.1 服务器 RUN ID2.3.2 复制偏移量 offset2.3.3 环形缓冲区 三、哨兵模式3.1 原理3.2 配置3.3 流程3.4 使用3.5 缺点 四、cluster集群4.1 原理…...

在GitHub上管理和协作的完全指南
介绍 GitHub 是一个强大的版本控制和协作平台,它不仅可以帮助你管理和跟踪项目的变化,还可以与他人进行协作。本文将详细介绍如何使用 GitHub 的各种功能来管理和协作项目。 目录 注册GitHub账号创建和管理仓库 创建仓库添加和管理文件分支管理合并请…...

git管理工具学习(图解使用git工作流程)
目录 GIT 简介一个最简单的GIT操作流程git的工作流程&命令 GIT 简介 git是什么,在维基百科上是这么介绍的:git是一个分布式的版本控制软件 分布式是相对于集中式而言的,分布式即每一个git库都是一个完整的库。 每个库的地位都是平等的&am…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...
