数据结构 | 递归
目录
一、何谓递归
1.1 计算一列数之和
1.2 递归三原则
1.3 将整数转换成任意进制的字符串
二、栈帧:实现递归
三、递归可视化
四、谢尔平斯基三角形
五、复杂的递归问题
六、动态规划
一、何谓递归
递归是解决问题的一种办法,它将问题不断地分成更小的子问题,直到子问题可以用普通的方法解决。
1.1 计算一列数之和
假设需要计算数字列表[1,3,5,7,9]的和。
循环求和函数如下:
def listsum(numList):theSum=0for i in numList:theSum=theSum+ireturn theSum递归求和函数如下:(递归调用)
def listsum(numList):if len(numList)==1:return numList[0]else:return numList[0]+listsum(numList[1:])1.2 递归三原则
所有的递归算法都要遵守的三个重要原则如下:
(1)递归算法必须有基本情况;
(2)递归算法必须改变其状态并向基本情况靠近;
(3)递归算法必须递归地调用自己。
基本情况是指使算法停止递归的条件,这通常是小到足以直接解决的问题。
为了遵守第二条原则,必须设法改变算法的状态,从而使其向基本情况靠近。改变状态是指修改算法所用的某些数据,这通常意味着代表问题的数据以某种方式变得更小。
最后一条原则是递归算法必须对自身进行调用。
1.3 将整数转换成任意进制的字符串
利用递归将整数转换成以2~16为进制基数的字符串的代码如下:
def toStr(n,base):converString="0123456789ABCDEF"if n<base:return converString[n]else:return toStr(n//base,base)+converString[n%base]二、栈帧:实现递归
假设不拼接递归调用toStr的结果和converString的查找结果,而是在进行递归调用之前把字符串压入栈中。
rStack=Stack()def toStr(n,base):converString="0123456789ABCDEF"if n<base:rStack.push(converString[n])else:rStack.push(converString[n%base])toStr(n//base,base)当调用函数时,Python分配一个栈帧来处理该函数的局部变量。当函数返回时,返回值就在栈的顶端,以供调用者访问。
栈帧限定了函数所用变量的作用域。尽管反复调用相同的函数,但是每一次调用都会为函数的局部变量创建新的作用域。
三、递归可视化
我们将使用Python的turtle模块来绘制图案。
使用turtle模块绘制螺旋线的代码如下。先导入turtle模块,然后创建一个小乌龟对象,同时也会创建用于绘制图案的窗口。接下来定义drawSpiral函数。这个简单函数的基本情况是,要画的线的长度(参数len)降为0。如果线的长度大于0,就让小乌龟向前移动len个单位距离,然后向右转90度。递归发生在用缩短后的距离再一次调用drawSpiral函数时。在结尾处调用了myWin.exitonclick()函数,这使小乌龟进入等待模式,直到用户在窗口内再次点击之后,程序清理并退出。
from turtle import *myTurtle=Turtle()
myWin=myTurtle.getscreen()def drawSpiral(myTurtle,lineLen):if lineLen>0:myTurtle.forward(lineLen)myTurtle.right(90)drawSpiral(myTurtle,lineLen-5)drawSpiral(myTurtle,100)
myWin.exitonclick()
接下来绘制一颗分形树。分形是数学的一个分支,它与递归有很多共同点。分形的定义是,不论放大多少倍来观察分形图,它总是有相同的基本形状。
绘制分形图的代码如下:
def tree(branchLen,t):if branchLen>5:t.forward(branchLen)t.right(20)tree(branchLen-15,t)t.left(40)tree(branchLen-10,t)t.right(20)t.backward(branchLen)from turtle import *
t=Turtle()
myWin=t.getscreen()
t.left(90)
t.up()
t.backward(300)
t.down()
t.color('green')
tree(110,t)
myWin.exitonclick()
四、谢尔平斯基三角形
from turtle import *def drawTriangle(points,color,myTurtle):myTurtle.fillcolor(color)myTurtle.up()myTurtle.goto(points[0])myTurtle.down()myTurtle.begin_fill()myTurtle.goto(points[1])myTurtle.goto(points[2])myTurtle.goto(points[0])myTurtle.end_fill()def getMid(p1,p2):return ((p1[0]+p2[0])/2,(p1[1]+p2[1])/2)def sierpinski(points,degree,myTurtle):colormap=['blue','red','green','white','yellow','violet','orange']drawTriangle(points,colormap[degree],myTurtle)if degree>0:sierpinski([points[0],getMid(points[0],points[1]),getMid(points[0],points[2])],degree-1,myTurtle)sierpinski([points[1], getMid(points[0], points[1]), getMid(points[1], points[2])], degree - 1, myTurtle)sierpinski([points[2], getMid(points[2], points[1]), getMid(points[0], points[2])], degree - 1, myTurtle)myTurtle=Turtle()
myWin=myTurtle.getscreen()
myPoints=[(-500,250),(0,500),(500,-250)]
sierpinski(myPoints,5,myTurtle)
myWin.exitonclick()五、复杂的递归问题
汉诺塔问题
假设一共有三根柱子,第一根柱子起初有5个盘子,任务是将5个盘子从一根柱子移动到另一根柱子,同时有两个重要的限制条件:每次只能移动一个盘子,并且大盘子不能放在小盘子之上。
如果我们知道如何把上面4个盘子移动到第二根柱子上,那么久轻易地把最底下的盘子移动到第三根柱子上,然后将4个盘子从第二根柱子移动到第三根柱子。但是如果不知道如何移动4个盘子,该怎么办呢?如果我们知道如何把上面的3个盘子移动到第三根柱子上,那么就轻易地把第4个盘子移动到第二根柱子上,然后再把3个盘子从第三个柱子上移动到第二根柱子上。但是如果不知道如何移动3个盘子,该怎么办呢?移动两个盘子到第二根柱子上,然后把第3个盘子移动到第三个柱子上,最后把两个盘子移过来,怎么样?但是如果还是不知道如何移动两个盘子,该怎么办呢?把一个盘子移动到第三个柱子并不难,甚至太简单了。这看上去就是这个问题的基本情况。
以下概述如何借助一根中间柱子,将高度为height的一叠盘子从起点柱子移到终点柱子:
(1)借助终点柱子,将高度为height-1的一叠盘子移到中间柱子;
(2)将最后一个盘子移到终点柱子;
(3)借助起点柱子,将高度为height-1的一叠盘子从中间柱子移到终点柱子。
def moveTower(height,fromPole,toPole,withPole):if height>=1:moveTower(height-1,fromPole,withPole,toPole)moveDisk(fromPole,toPole)moveTower(height-1,withPole,toPole,fromPole)def moveDisk(fp,tp):print("moving disk from %d to %d\n"%(fp,tp))汉诺塔问题的详细讲解(python版)![]() https://blog.csdn.net/wistonty11/article/details/123563309
https://blog.csdn.net/wistonty11/article/details/123563309
六、动态规划
在解决优化问题时,一个策略是动态规划。
优化问题的一个经典例子就是在找零时使用最少的硬币。假设某个自动售货机制造商希望在每笔交易中给出最少的硬币。一个顾客使用一张一美元的纸币购买了价值37美元的物品,最少需要找给该顾客多少硬币呢?答案是6枚:25美分的2枚,10美分的1枚,1美分的3枚。该如何计算呢?从面值最大的硬币(25美分)开始,使用尽可能多的硬币,然后尽可能地使用面值第2大的硬币。这种方法叫做贪婪算法——试图最大程度地解决问题。
算法基础:贪婪算法(基于Python)![]() https://blog.csdn.net/leowinbow/article/details/88140107让我们来考察一种必定能得到最优解的方法。这是一种递归方法。首先确定基本情况:如果要找的零钱金额与硬币面值相同,那么只需找1枚硬币即可。
https://blog.csdn.net/leowinbow/article/details/88140107让我们来考察一种必定能得到最优解的方法。这是一种递归方法。首先确定基本情况:如果要找的零钱金额与硬币面值相同,那么只需找1枚硬币即可。
如果要找的零钱硬币和硬币的面值不同,则有多种选择:1枚1分的硬币加上找零钱金额减去1分之后所需的硬币;1枚5分的硬币加上找零金额减去5分之后所需的硬币;1枚10分的硬币加上找零金额减去10分之后所需的硬币;1枚25分的硬币加上找零金额减去25分之后所需的硬币。我们需要从中找到硬币数最少的情况,如下所示:
numCoins=min(1+numCoins(originalamount-1),1+numCoins(originalamount-5),1+numCoins(originalamount-10),1+numCoins(originalamount-20))找零问题的递归解决方案如下:
def recMC(coinValueList,change):minCoins=changeif change in coinValueList:return 1else:for i in [c for c in coinValueList if c<=change]:numCoins=1+recMC(coinValueList,change-i)if numCoins<minCoins:minCoins=numCoinsreturn minCoinsrecMC([1,5,10,25],63)显然,该算法将大量时间和资源浪费在了重复计算已有的结果上。
减少计算量的关键在于记住已有的结果。简单的做法是把最少硬币数的计算结果存储在一张表中,并在计算新的最少硬币数之前,检查结果是否已在表中。如果是,就直接使用结果,而不是重新计算。
添加查询表之后的找零算法:
def recDC(coinValueList,change,knownResults):minCoins=changeif change in coinValueList:knownResults[change]=1return 1elif knownResults[change]>0:return knownResults[change]else:for i in [c for c in coinValueList if c<=change]:numCoins=1+recDC(coinValueList,change-i,knownResults)if numCoins<minCoins:minCoins=numCoinsknownResults[change]=minCoinsreturn minCoinsrecDC([1,5,10,25],63,[0]*64)上面所做的优化并不是动态规划,而是通过记忆化(或者叫作缓存)的方法来优化程序的性能。
真正的动态规划算法会用更系统化的方法来解决问题。在解决找零问题时,动态规划算法会从1分找零开始,然后系统地一直计算到所需的找零金额。这样做可以保证在每一步都已经知道任何小于当前值的找零金额所需的最少硬币数。
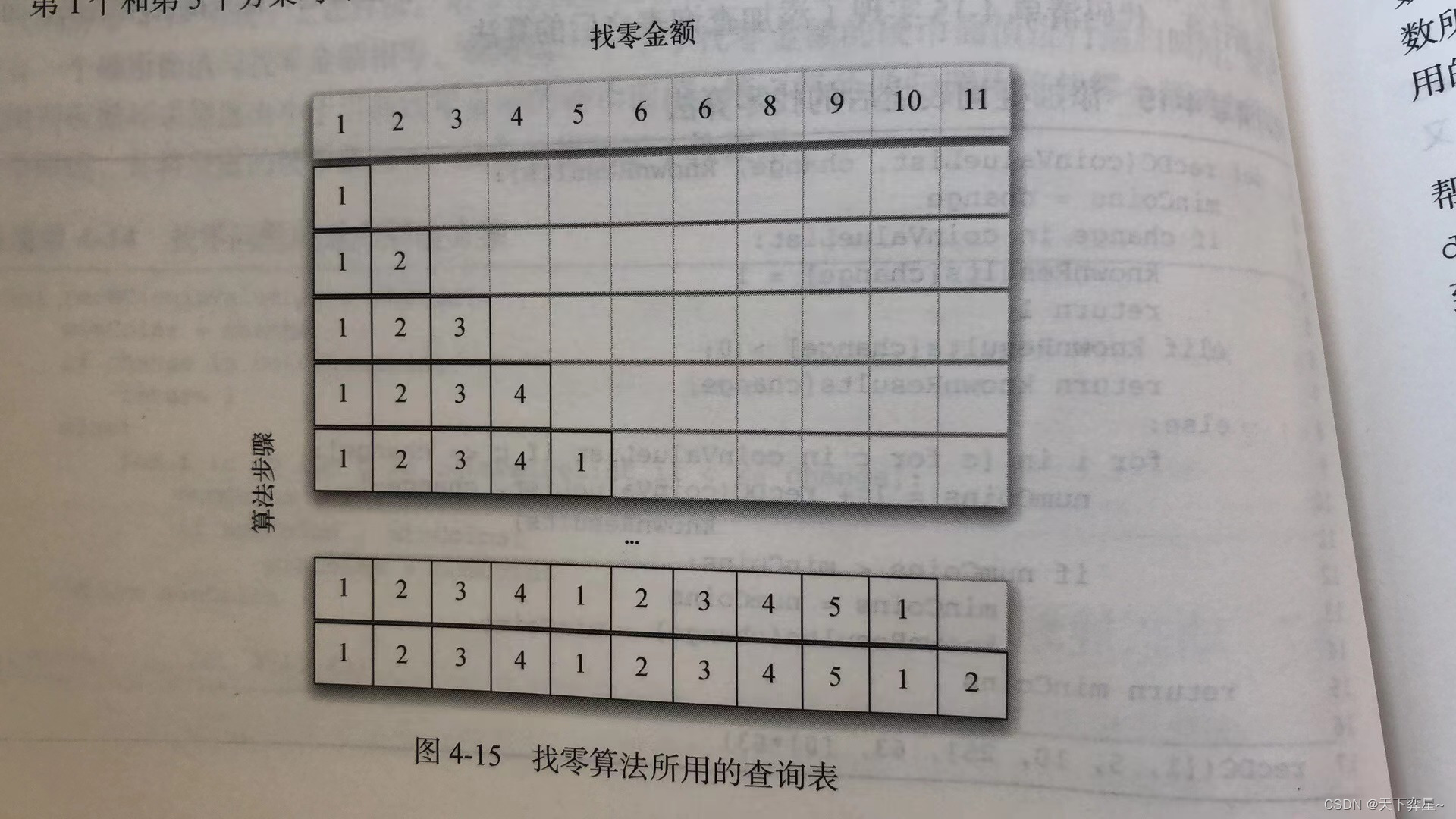
 在这个过程中,从1分开始,只需找1枚1分的硬币。第2行展示了1分和2分所需的最少硬币数。同理,2分只需找2枚1分的硬币。第5行开始变得有趣起来,此时我们有2个可选方案:要么找5枚1分的硬币,要么找1枚5分的硬币。哪个方案更好呢?查表后发现,4分所需的最少硬币数是4,再加上1枚1分的硬币就得到5分(共需要5枚硬币);如果直接找1枚5分的硬币,则最少硬币数是1.由于1比5小,因此我们把1存入表中。接着来看11分的情况,我们有3个可选方案:
在这个过程中,从1分开始,只需找1枚1分的硬币。第2行展示了1分和2分所需的最少硬币数。同理,2分只需找2枚1分的硬币。第5行开始变得有趣起来,此时我们有2个可选方案:要么找5枚1分的硬币,要么找1枚5分的硬币。哪个方案更好呢?查表后发现,4分所需的最少硬币数是4,再加上1枚1分的硬币就得到5分(共需要5枚硬币);如果直接找1枚5分的硬币,则最少硬币数是1.由于1比5小,因此我们把1存入表中。接着来看11分的情况,我们有3个可选方案:
(1)1枚1分的硬币加上找10分零钱(11-1)最少需要的硬币(1枚)。
(2)1枚5分的硬币加上找6分零钱(11-5)最少需要的硬币(2枚)。
(3)1枚10分的硬币加上找1分零钱(11-10)最少需要的硬币(1枚)。
第1个和第3个方案均可得到最优解,即共需要2枚硬币。
找零问题的动态规划解法代码如下所示。dpMakeChange接受3个参数:硬币面值列表、找零金额,以及由每一个找零金额所需的最少硬币数构成的列表。当函数运行结束时,minCoins将包含找零金额从0到change的所有最优解。
def dpMakeChange(coinValueList,change,minCoins):for cents in range(change+1):coinCount=centsfor j in [c for c in coinValueList if c<=cents]:if minCoins[cents-j]+1<coinCount:coinCount=minCoins[cents-j]+1minCoins[cents]=coinCountreturn minCoins[change]dpMakeChange并不是递归函数。
修改后的动态规划解法:
def dpMakeChange(coinValueList,change,minCoins,coinsUsed):for cents in range(change+1):coinCount=centsnewCoin=1for j in [c for c in coinValueList if c<=cents]:if minCoins[cents-j]+1<coinCount:coinCount=minCoins[cents-j]+1newCoin=jminCoins[cents]=coinCountcoinsUsed[cents]=newCoinreturn minCoins[change]def printCoins(coinsUsed,change):coin=changewhile coin>0:thisCoin=coinsUsed[coin]print(thisCoin)coin=coin-thisCoincl=[1,5,10,21,25]
coinsUsed=[0]*64
coinCount=[0]*64
dpMakeChange(cl,63,coinCount,coinsUsed)
print(printCoins(coinsUsed,63))
print(printCoins(coinsUsed,52))
print(coinsUsed)运行结果如下:
21
21
21
None
10
21
21
None
[1, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 21, 1, 1, 1, 25, 1, 1, 1, 1, 5, 10, 1, 1, 1, 10, 1, 1, 1, 1, 5, 10, 21, 1, 1, 10, 21, 1, 1, 1, 25, 1, 10, 1, 1, 5, 10, 1, 1, 1, 10, 1, 10, 21]动态规划(Dynamic programming)详解![]() https://blog.csdn.net/qq_37771475/article/details/126855564
https://blog.csdn.net/qq_37771475/article/details/126855564
相关文章:
数据结构 | 递归
目录 一、何谓递归 1.1 计算一列数之和 1.2 递归三原则 1.3 将整数转换成任意进制的字符串 二、栈帧:实现递归 三、递归可视化 四、谢尔平斯基三角形 五、复杂的递归问题 六、动态规划 一、何谓递归 递归是解决问题的一种办法,它将问题不断地分…...

微信发视频怎么不压缩画质?试试这几招
微信是我们常用的社交工具了,很多朋友都会用它跟好友分享视频,但想必大家都知道,微信为了节省宽带和存储空间,会自动对上传的视频进行压缩处理,甚至过大的视频会被限制发送,怎么才能让微信不自动压缩画质呢…...
【网络安全带你练爬虫-100练】第16练:使用session发送请求
目录 一、目标1:使用seesion进去请求 二、网络安全O 一、目标1:使用seesion进去请求 (1)应用: 通过创建会话(session)对象来请求并爬取返回的数据包 情景:需要登录才能爬取的网…...

论文代码学习—HiFi-GAN(3)——模型损失函数loss解析
文章目录 引言正文生成器损失函数最小二乘损失函数梅尔频谱图损失函数特征匹配损失函数生成器最终损失函数loss生成器loss对应代码 鉴定器损失函数鉴定器损失函数代码 总结引用 引言 这里翻译了HiFi-GAN这篇论文的具体内容,具体链接。这篇文章还是学到了很多东西&a…...
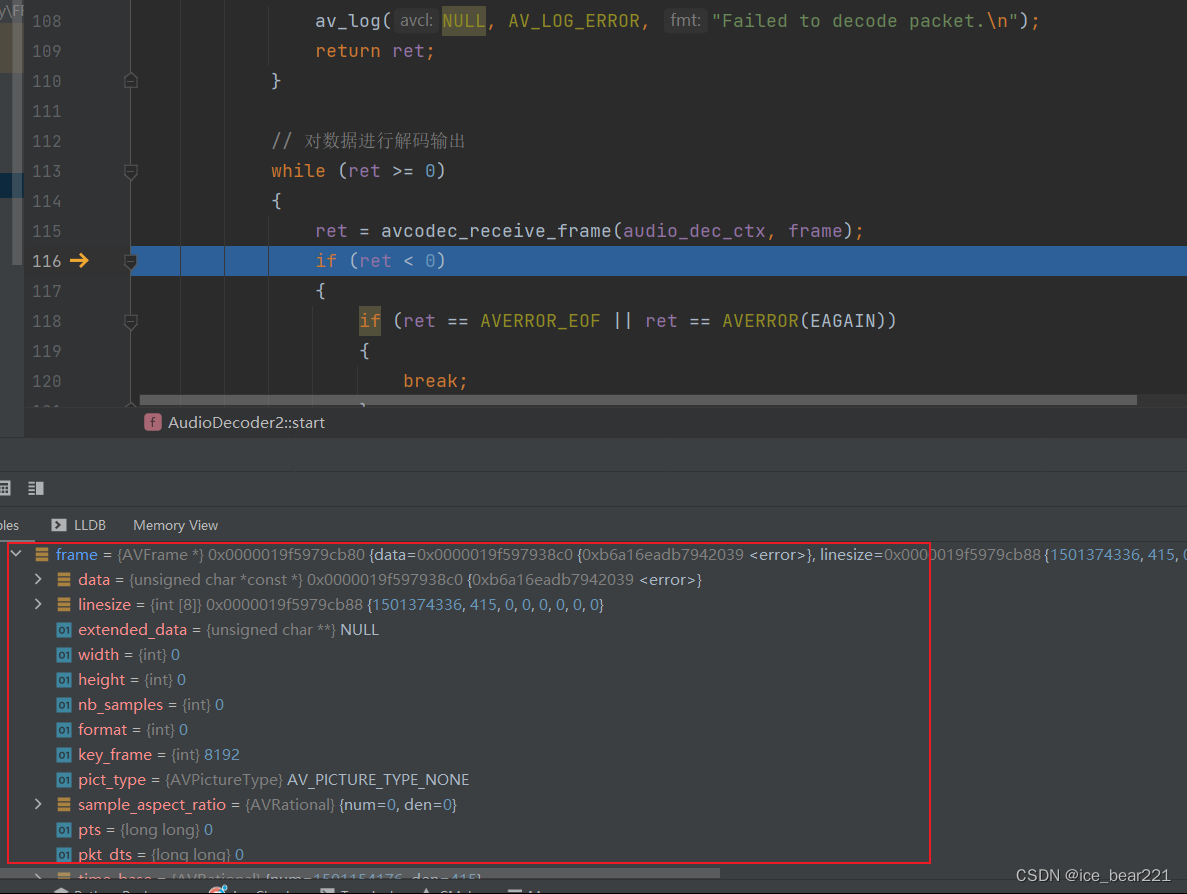
CLion中avcodec_receive_frame()问题
1. 介绍 在提取音视频文件中音频的PCM数据时,使用avcodec_receive_frame()函数进行解码时,遇到了一些问题,代码在Visual Studio 2022中运行结果符合预期,但是在CLion中运行时,获取的AVFrame有错误,和VS中获…...
Linux安装操作(Mac版本)
Parallels Desktop的简介 Parallels Desktop是Mac平台上的虚拟机软件,也是Mac平台最好的虚拟机软件之一。它允许用户在Mac OS X系统上同时运行其他操作系统,例如Windows、Linux等。Parallels Desktop为Mac用户提供了使用其他操作系统和软件的便利性&…...
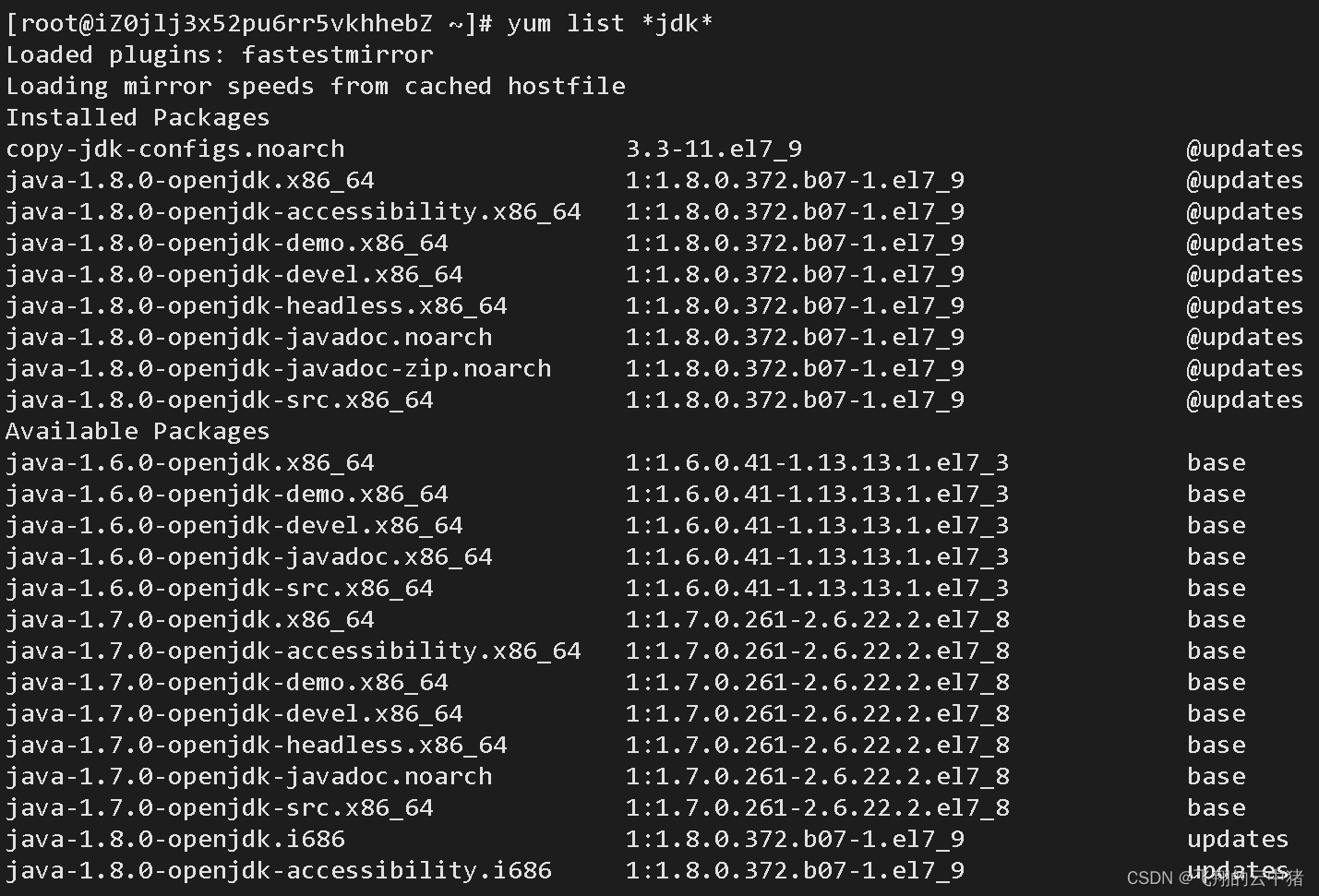
Linux(四)--包软件管理器与Linux上软件的下载示例
一.包软件管理器【yum和apt】 1.先来学习使用yum命令。yum:RPM包软件管理器,用于自动化安装配置Linux软件,并可以自动解决依赖问题。通过yum命令我们可以轻松实现软件的下载,查找,卸载与更新等管理软件的操作。 最常用…...

HTML <param> 标签
实例 向 HTML 代码添加一个对象: <object classid="clsid:F08DF954-8592-11D1-B16A-00C0F0283628" id="Slider1" width="100" height="50"><param name="BorderStyle" value="1" /><param nam…...
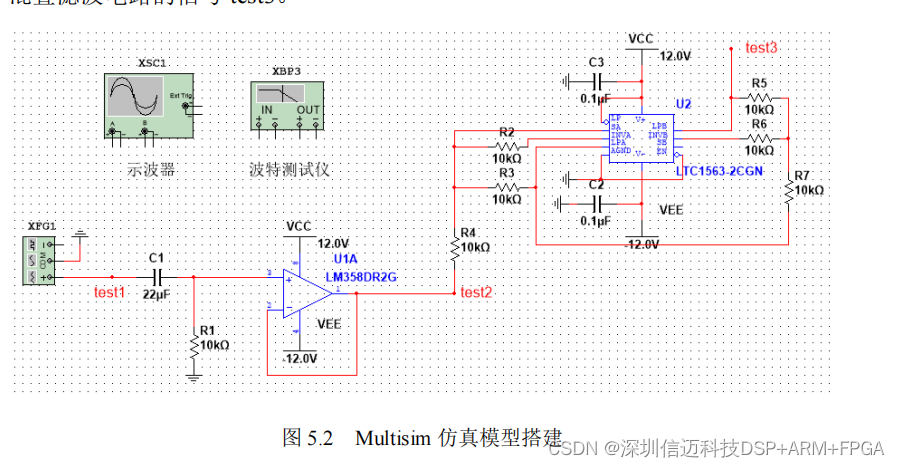
基于ARM+FPGA (STM32+ Cyclone 4)的滚动轴承状态监测系统
状态监测系统能够在故障早期及时发现机械设备的异常状态,避免故障的 进一步恶化造成不必要的损失,滚动轴承是机械设备的易损部件,本文对以滚动 轴承为研究对象的状态监测系统展开研究。现有的监测技术多采用定时上传监 测数据,…...

二、数据结构10:堆 模板题+算法模板(堆排序,模拟堆)
文章目录 算法模板堆题目代码模板堆的原理down操作理解:up操作理解建堆操作关于heap_swap中存的映射数组理解(模拟堆题目中用到) 模板题堆排序原题链接题目思路题解 模拟堆原题链接题目思路题解 算法模板 堆题目代码模板 // h[N]存储堆中的…...
W6100-EVB-PICO做DNS Client进行域名解析
前言 在上一章节中我们用W6100-EVB-PICO通过dhcp获取ip地址(网关,子网掩码,dns服务器)等信息,给我们的开发板配置网络信息,成功的接入网络中,那么本章将教大家如何让我们的开发板进行DNS域名解…...

【linux-网络】4层转发方法-iptable以及nginx
1.背景 有时候远程或者某些业务需要做转发就会用到iptables或者nginx,或者ss都可以 根据自己的情况去适配。 2.方法: 1)iptables -把linux内核转发功能打开 echo "net.ipv4.ip_forward1" >> /etc/sysctl.conf -出入转发…...

vue复制文案,复制图片,黏贴图片
vue 实现复制文案,复制图片,在微信聊天框,黏贴为图片 //安装 cnpm i clipboard-all //引用 import clipboard from clipboard-all<!-- row.url 图片路径 --><div ref"foo" class"hidden"><img :src"…...

Web应急思路
Web应急思路 找到webshell --> 确定攻击者IP --> 回溯攻击者操作 --> 梳理整个攻击过程 1.寻找webshell方法 1.文件内容中的恶意函数 2.web日志中的webshell特征 3.贴合web业务中的URL来分析web日志 4.源码版本管理对比,注重修改或新增的脚本文件 5.统计…...
shell脚本清理redis模糊匹配的多个key,并计算释放内存大小
#!/bin/bash# 定义Redis服务器地址和端口 REDIS_HOST"localhost" REDIS_PORT6380# 获取Redis当前内存使用量(以字节为单位) function get_redis_memory_usage() {redis-cli -h $REDIS_HOST -p $REDIS_PORT INFO memory | grep "used_memo…...

python-MySQL数据库建表语句(需要连接数据库)转存为Excel文档-工作小记
将create table XXXXXX 转为指定Excel文档。该脚本适用于数据库表结构本地文档记录 呈现效果 代码 # -*- coding:utf-8 -*- # Time : 2023/8/2 15:14 # Author: 水兵没月 # File : MySQL建表_2_excel.py import reimport mysql.connector import pandas as pd db 库名 mydb …...

iOS Block介绍
文章目录 一、Block定义二、block为什么用copy修饰三、block使用时的注意事项四、使用 block时什么情况会发生引用循环,如何解决?五、在block内如何修改block外部变量?六、__block与__weak的区别 一、Block定义 目的就是能够直接存储一个代码…...

小程序安全性加固:如何保护用户数据和防止恶意攻击
第一章:引言 在当今数字化时代,移动应用程序的使用已经成为人们日常生活中的重要组成部分。小程序作为一种轻量级的应用程序形式,受到了广泛的欢迎。然而,随着小程序的流行,安全性问题也日益凸显。用户数据泄露和恶意攻…...

Ubuntu的tar命令详解
在 Ubuntu 中压缩文件夹可以使用 tar 命令。tar 可以将多个文件或文件夹打成一个包,并可选是否进行压缩,最常用的压缩方式是 gzip 和 bzip2。 常用的 tar 命令参数如下: -c:创建新的 tar 包; -x:解压 tar…...
使用elementplus实现文本框的粘贴复制
需求: 文本框仅用于显示展示数据并且用户可以进行复制,并不会进行修改和编辑, 注意点: 1.首先且文本为多行。所以不能使用普通的el-input,这种一行超出就会隐藏了,如果多行超出行数也会隐藏(…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
