刷题记录:牛客NC14402求最大值
传送门:牛客
题目描述:
给出一个序列,你的任务是求每次操作之后序列中 (a[j]-a[i])/(j-i)【1<=i<j<=n】的最大值。
操作次数有Q次,每次操作需要将位子p处的数字变成y.
输入:
5
2 4 6 8 10
2
2 5
4 9
输出:
3.00
3.00
对于本题,首先我们得分析出这道题的式子的巧妙之处才能动手
对于区间内任意的i,ji,ji,j,假设i,ji,ji,j直接没有夹杂其他的数字,那么此处我们的式子的值就是a[j]−a[i]a[j]-a[i]a[j]−a[i],假设我们的i,ji,ji,j之间存在a1,a2,a3,a4a1,a2,a3,a4a1,a2,a3,a4,此时我们的式子就可以表示为
(a[j]−a4+a4−a3+a3−a2+a2−a1+a1−a[i])/6(a[j]-a4+a4-a3+a3-a2+a2-a1+a1-a[i])/6(a[j]−a4+a4−a3+a3−a2+a2−a1+a1−a[i])/6,此时我们会显然的发现这个式子就是我们i,ji,ji,j之间的所有相邻的数字的差的和的平均值.对于这个平均值来说,显然取最大的差是我们的这个式子最大的时候.
那么此时这道题就变成了如何维护区间内相邻两个数的差的最大值
我们可以线段树来维护这个值.考虑使用mxmxmx来表示区间内相邻两个数的差的最大值
使用lnumlnumlnum来表示区间的左端点的数字,为了区间合并方便
使用rnumrnumrnum来表示区间的右端点的数字,为了区间合并方便
对于区间合并,我们会发现显然我们的大区间的mxmxmx有三种情况,1.左区间的mxmxmx 2.右区间的mxmxmx 3.有区间的lnumlnumlnum-左区间的rnumrnumrnum 三者取一个maxmaxmax维护即可
对于updateupdateupdate,queryqueryquery,简单的单点修改和区间查询,此处就不再赘述了
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 200100
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{int l,r;int mx;int lnum,rnum;
}tree[maxn*4];
int n,m;int a[maxn];
void pushup(Segment_tree &u,Segment_tree &l,Segment_tree &r) {u.l=l.l;u.r=r.r;u.lnum=l.lnum;u.rnum=r.rnum;u.mx=max(l.mx,r.mx);u.mx=max(u.mx,r.lnum-l.rnum);
}
void pushup(int rt) {pushup(tree[rt],tree[ls],tree[rs]);
}
void build(int l,int r,int rt) {tree[rt].l=l;tree[rt].r=r;tree[rt].mx=-int_INF;if(l==r) {tree[rt].lnum=tree[rt].rnum=a[l];return ;}int mid=(l+r)>>1;build(lson);build(rson);pushup(rt);
}
void update(int pos,int v,int rt) {if(tree[rt].l==pos&&tree[rt].r==pos) {tree[rt].lnum=tree[rt].rnum=v;return ;}int mid=(tree[rt].l+tree[rt].r)>>1;if(pos<=mid) update(pos,v,ls);else update(pos,v,rs);pushup(rt);
}
int main() {while(scanf("%d",&n)!=EOF) {for(int i=1;i<=n;i++) a[i]=read();build(root);m=read();for(int i=1;i<=m;i++) {int pos=read(),v=read();update(pos,v,1);printf("%.2lf\n",(double)tree[1].mx);}}return 0;
}
相关文章:

刷题记录:牛客NC14402求最大值
传送门:牛客 题目描述: 给出一个序列,你的任务是求每次操作之后序列中 (a[j]-a[i])/(j-i)【1<i<j<n】的最大值。 操作次数有Q次,每次操作需要将位子p处的数字变成y. 输入: 5 2 4 6 8 10 2 2 5 4…...

javaEE 初阶 — 传输层 TCP 协议 中的延迟应答与捎带应答
文章目录1. 延迟应答2. 捎带应答TCP 工作机制:确认应答机制 超时重传机制 连接管理机制 滑动窗口 流量控制与拥塞控制 1. 延迟应答 延时应答 也是提升效率的机制,也是在滑动窗口基础上搞点事情。 滑动窗口的关键是让窗口大小大一点,传输…...
STM32单片机初学8-SPI flash(W25Q128)数据读写
当使用单片机进行项目开发,涉及大量数据需要储存时(例如使用了屏幕作为显示设备,常常需要存储图片、动画等数据),单靠单片机内部的Flash往往是不够用的。 如STM32F103系列,内部Flash最多只能达到512KByte&a…...

MS-SQL创建查询排序语句总结
重新捡起枪杆子,学习N年没用过的MS-SQL,整理一些学习笔记记录。 一、创建、修改和删除表 在SQL中,表有如下规则: 每张表都有一个名字,通常称为表名或关系名。表名必须以字母开头,最大长度为 30 个字符。一…...

subprocess—Python多进程模块
subprocess—Python多进程模块 1.概述 这篇文章介绍并行运算中的subprocess模块,subprocess 模块允许我们启动一个新进程,并连接到它们的输入/输出/错误管道,从而获取返回值。 subprocess 它可以用来调用第三方工具(例如&#x…...
【APP渗透测试】 Android APP渗透测试技术实施以及工具使用(客户端服务端)
文章目录前言一、安全威胁分析二、主要风险项三、Android测试思维导图四、反编译工具五、Android客户端漏洞一、Jnaus漏洞漏洞二、数据备份配置风险漏洞漏洞三、Activity组件泄露漏洞漏洞四、BroadcastReceiver组件泄露漏洞漏洞五、允许模拟器Root环境登录漏洞漏洞六、未识别代…...
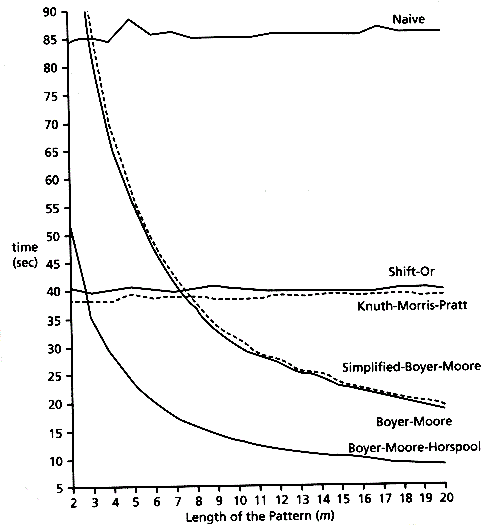
字符串匹配 - Overview
字符串匹配(String Matchiing)也称字符串搜索(String Searching)是字符串算法中重要的一种,是指从一个大字符串或文本中找到模式串出现的位置。字符串匹配概念字符串匹配问题的形式定义:文本(Text)是一个长度为 n 的数组 T[1..n]&…...
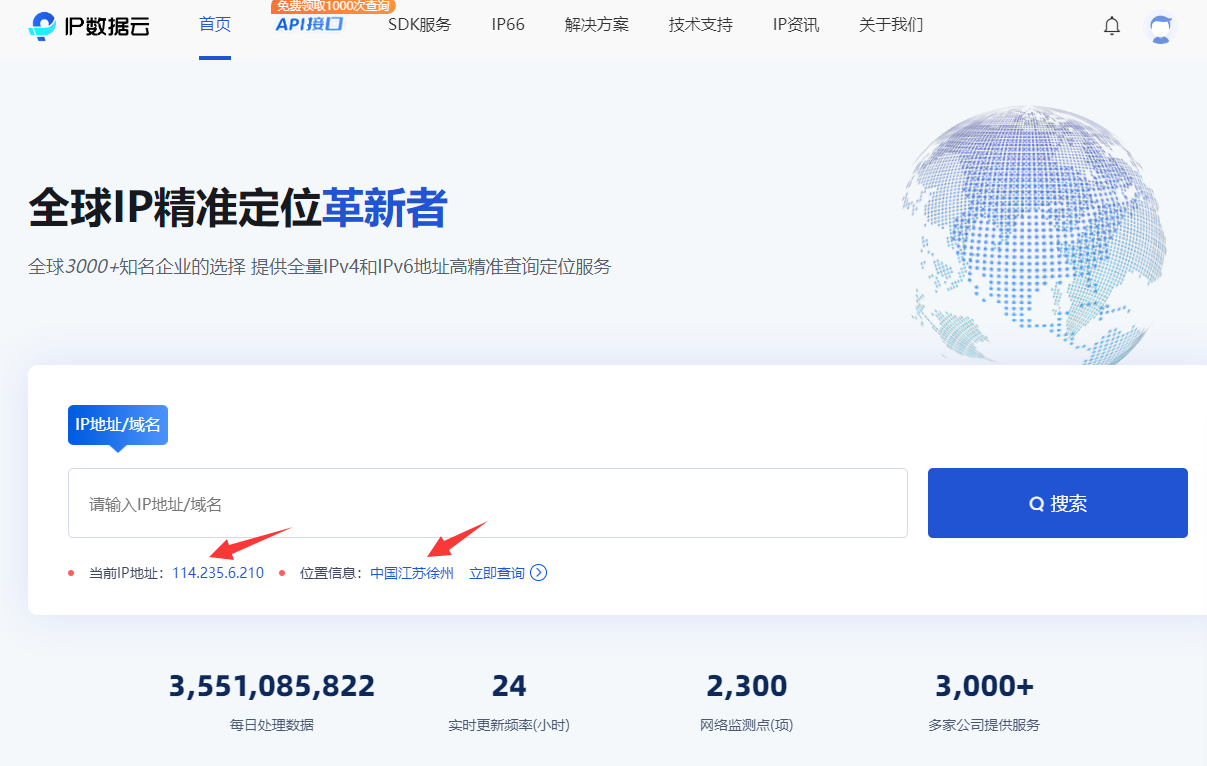
【IP课堂】Ip地址如何进行精准定位?
通过Ip地址定位,是目前网络上最常见的定位方式。当然,也是最简单的定位方式。其实方法大多都是雷同的,通过Ip定位,就目前网上公开的技术。如通过搜索关键词“定位,定位查询,Ip定位”等,只能查询…...

MySQL 临时表相关参数说明区别
MySQL 临时表参数innodb_temp_tablespaces_dir、innodb_temp_data_file_path、innodb_tmpdir、tmpdir 区分 解决方案 innodb_tmpdir: alter table生成中间表文件,innodb_tmpdir有指定效路径,优选选择innodb_tmpdir,没有则选择tm…...

第二章 变量和基本类型
1.string类型数据的另一种初始化方式 语法: string 变量名 (" 初始化内容 "); 2.C中的列表初始化 语法: 数据类型 变量名 { 变量初始化的值 } ; 数据类型 变量名 { 变量初始化的值 } ; 例: 3.引用常量 常量引…...

【Python】循环语句(while,for)、运算符、字符串格式化
一、while循环Python 编程中 while 语句用于循环执行程序,即在某条件下,循环执行某段程序,以处理需要重复处理的相同任务。其基本形式为:while 判断条件(condition):执行语句(statements)执行语句可以是单个语句或语句…...

利用设计模式、反射写代码
软件工程师和码农最大的区别就是平时写代码时习惯问题,码农很喜欢写重复代码而软件工程师会利用各种技巧去干掉重复的冗余代码。 业务同学抱怨业务开发没有技术含量,用不到设计模式、Java 高级特性、OOP,平时写代码都在堆 CRUD,个…...

Spring Cloud Alibaba--seata微服务详解之分布式事务(三)
上篇讲述gateway的部署和使用,gateway统一管理和转发了HTTP请求,在互联网中大型项目一定存在复杂的业务关系,尤其在商城类软件中如淘宝、PDD等商城,尤其在秒杀场景中,并发量可以到达千万级别,此时数据库就会…...

[USACO2023-JAN-Bronze] T3 Moo Operations 题解
一、题目描述因为Bessie觉得玩平时经常玩的只包含C O和W的字符串无聊了,Farmer John 给了她Q个新的字符串(1≤Q≤100),这Q个字符串只包含M和O。很明显,只包含M和O的单词里Bessie最喜欢的是”MOO”,所以她希望按照下面两个规则&…...
OKCC呼叫中心支持哪些接入方式?
使用OKCC系统开展呼叫中心业务,要将电话打通,需要什么样的设备接入到OKCC系统呢? 目前实际广泛使用的接入方式,既有硬件网关接入方式,也有软件接入方式,在生产实践中,我们须根据实际的需求及使…...
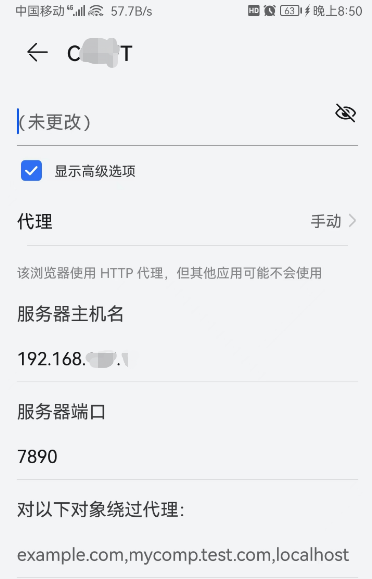
如何让手机共享电脑代理网络的WIFI热点
参考: 手机共享电脑的proxy网络 把电脑的网络代理给安卓设备如何将电脑的代理网络以WIFI热点的方式共享 电脑端设置代理: 打开电脑上的 proxy软件并设置其端口号(例如:7890),且允许局域网(例如…...

渲染有问题?怎么办?6种方法让你渲染无忧
简单点,解决问题的方式简单点。 日常工作中我们总会遇到各种各样的问题,比如渲不出图,速度太慢或效率太低,各种噪点和黑图等等,烦不胜烦,今天我就针对6个常见的问题给大家说下方法,一家之言仅供…...

中国人寿业务稳定性保障:“1+1+N” 落地生产全链路压测
引言 保险业务的数字化转型正如火如荼地进行,产品线上化、投保线上化、承保线上化、核保线上化等业务转型,导致系统的应用范围不断扩大,用户的高频访问也正在成为常态。同时,系统复杂性也呈指数上升,这些因素都增加了…...

2/17考试总结
时间安排 7:40–7:50 读题,T1 貌似是签到,T2,T4 DP,T3看起来很不可做。 7:50–8:00 T1,差分一下然后模拟就行了。 8:00–10:20 T2,注意到值域很小,可以考虑状压,想到一个状压状态数较少的 dp ,然后挂得彻底。发现有一…...
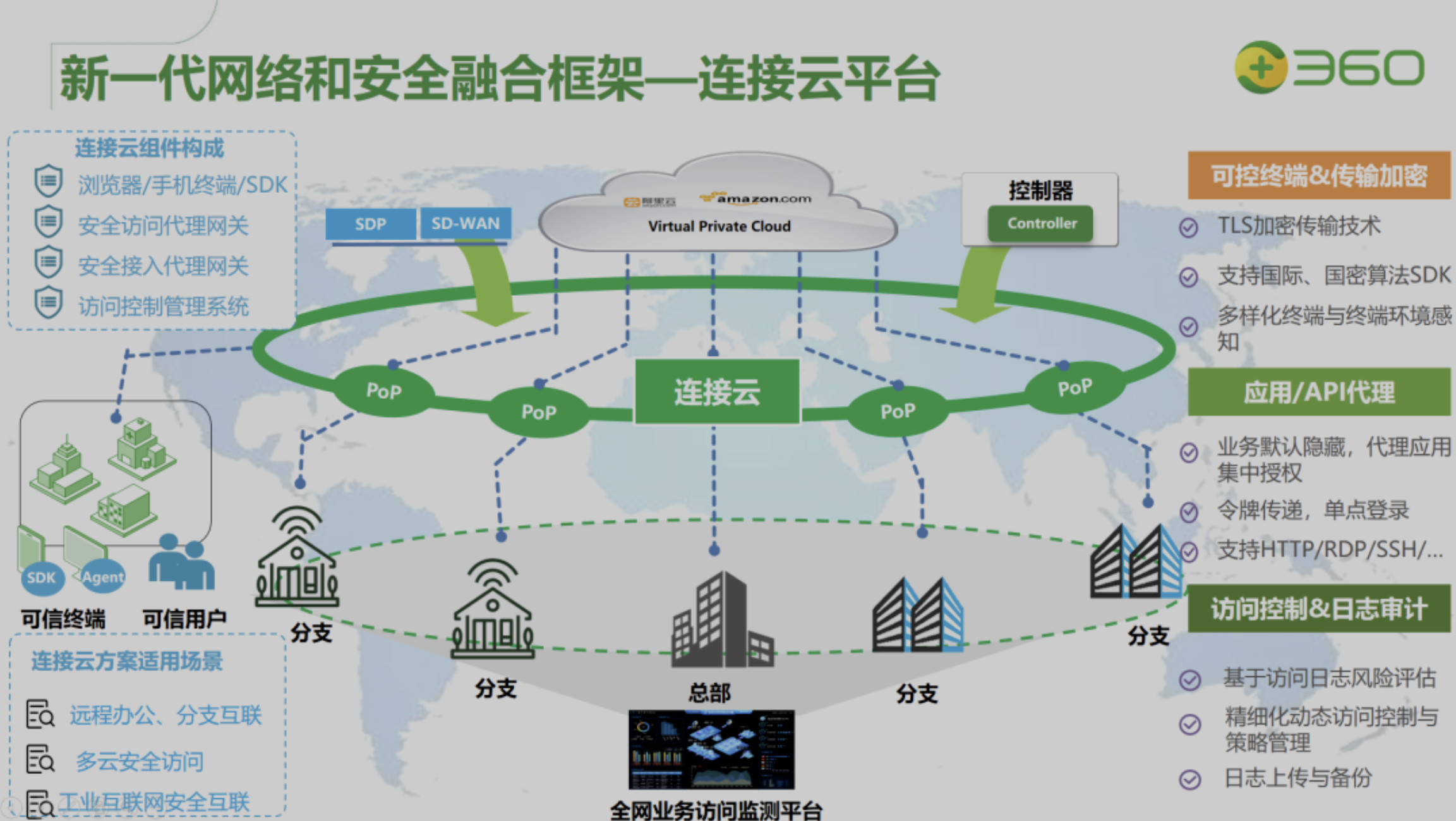
零信任-360连接云介绍(9)
360零信任介绍 360零信任又称360连接云安全访问平台(下文简称为:360连接云),360连接云,是360基于零信任安全理念,以身份为基础、动态访问控制为核心打造的安全访问平台。 通过收缩业务暴露面、自适应增强身份认证、终端持续检…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
