1243. 糖果/状态压缩dp【AcWing】
1243. 糖果
糖果店的老板一共有 M种口味的糖果出售。
为了方便描述,我们将 M种口味编号 1∼M。
小明希望能品尝到所有口味的糖果。
遗憾的是老板并不单独出售糖果,而是 K颗一包整包出售。
幸好糖果包装上注明了其中 K颗糖果的口味,所以小明可以在买之前就知道每包内的糖果口味。
给定 N包糖果,请你计算小明最少买几包,就可以品尝到所有口味的糖果。
输入格式
第一行包含三个整数 N,M,K。
接下来 N行每行 K个整数 T1,T2,⋅⋅⋅,TK,代表一包糖果的口味。
输出格式
一个整数表示答案。
如果小明无法品尝所有口味,输出 −1。
数据范围
1≤N≤100,
1≤M,K≤20,
1≤Ti≤M
输入样例:
6 5 3
1 1 2
1 2 3
1 1 3
2 3 5
5 4 2
5 1 2
输出样例:
2
状态压缩dp
状态压缩dp用位运算实现。
思路:
dp[ i ][ j ]表示前 i 袋糖果集齐 j 种糖果所需要的最少袋数。
可以选择第 i 袋或者不选择第 i 袋。
状态转移方程为:
dp[ i ][ j ]=min( dp[ i - 1 ][ j ] , dp[ i - 1 ][ j & (~ w[ i ])]+1 )
前面那个是不选择第 i 袋,比较好理解,后面那个可以举个例子
例如我们想要 j 为11011,而w[ i ]为 11100,取反后为00011,11011 & 00011 = 10000,故是从10000这个状态转移过来的。
然后要先预处理dp数组为100,dp[0]=0就可以了。
#include<bits/stdc++.h>
using namespace std;
int w[100],dp[1<<20];
int main()
{int n,m,k;cin>>n>>m>>k;int s=(1<<m)-1;for(int i=1;i<=n;i++){for(int j=1;j<=k;j++){int r;cin>>r;w[i]|=1<<r-1;}}for(int i=1;i<(1<<m);i++) dp[i]=100;dp[0]=0;for(int i=1;i<=n;i++){for(int j=(1<<m)-1;j>0;j--){dp[j]=min(dp[j],dp[j&(~w[i])]+1);}}(dp[s]==100)?(cout<<-1<<endl):(cout<<dp[s]<<endl);return 0;
}
相关文章:

1243. 糖果/状态压缩dp【AcWing】
1243. 糖果 糖果店的老板一共有 M种口味的糖果出售。 为了方便描述,我们将 M种口味编号 1∼M。 小明希望能品尝到所有口味的糖果。 遗憾的是老板并不单独出售糖果,而是 K颗一包整包出售。 幸好糖果包装上注明了其中 K颗糖果的口味,所以小…...
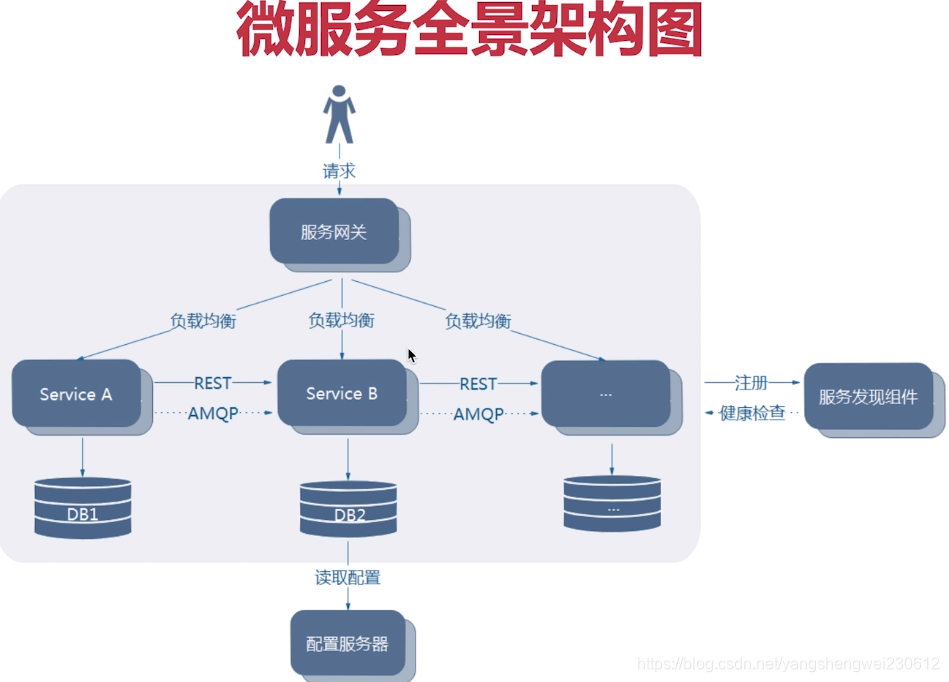
【Spring Cloud Alibaba】001-单体架构与微服务架构
【Spring Cloud Alibaba】001-单体架构与微服务 文章目录【Spring Cloud Alibaba】001-单体架构与微服务一、单体架构1、单体应用与单体架构2、单体应用架构图3、单体架构优缺点优点缺点二、微服务1、微服务的“定义”2、微服务的特性3、微服务架构图4、微服务的优缺点优点缺点…...

Renderer 使用材质分析:materials、sharedMaterials 及 MaterialPropertyBlock
一、materials 与 sharedMaterials 1.1 使用上的区别与差异 Unity 开发时,在 C# 中通过 Renderer 取材质操作是非常常见的操作,Renderer 有两种常规获取材质的方式: sharedMaterials:可以理解这个就是原始材质,所有使…...

java学习----网络编程
网络编程入门 网络编程概述 计算机网络 计算机网络是指地理位置不同的具有独立功能的计算机及其外部设备,通过通信线路连接起来,在网络操作系统,网络管理软件及网络通信协议的管理协调下,实现资源共享和信息传递的计算机系统…...

这些「误区」99%的研发都踩过
意识不到误区的存在最为离谱; 01生活中,职场上,游戏里,都少不了正面对喷过:意识太差; 在个人的认知中意识即思维,意识太差即思维中存在的误区比较多; 每个人或多或少都存在思维上的…...

Bi系统跟数据中台的区别是什么?
随着数据时代的发展,BI分析是当今数据时代必不可少的能力之一。BI系统通过系统化产品化的方法,能够大幅降低数据的获取成本、提升数据使用效率。同时借助可视化、交互式的操作,可以高效支持业务的分析及发展。 BI如此火热,随之而…...
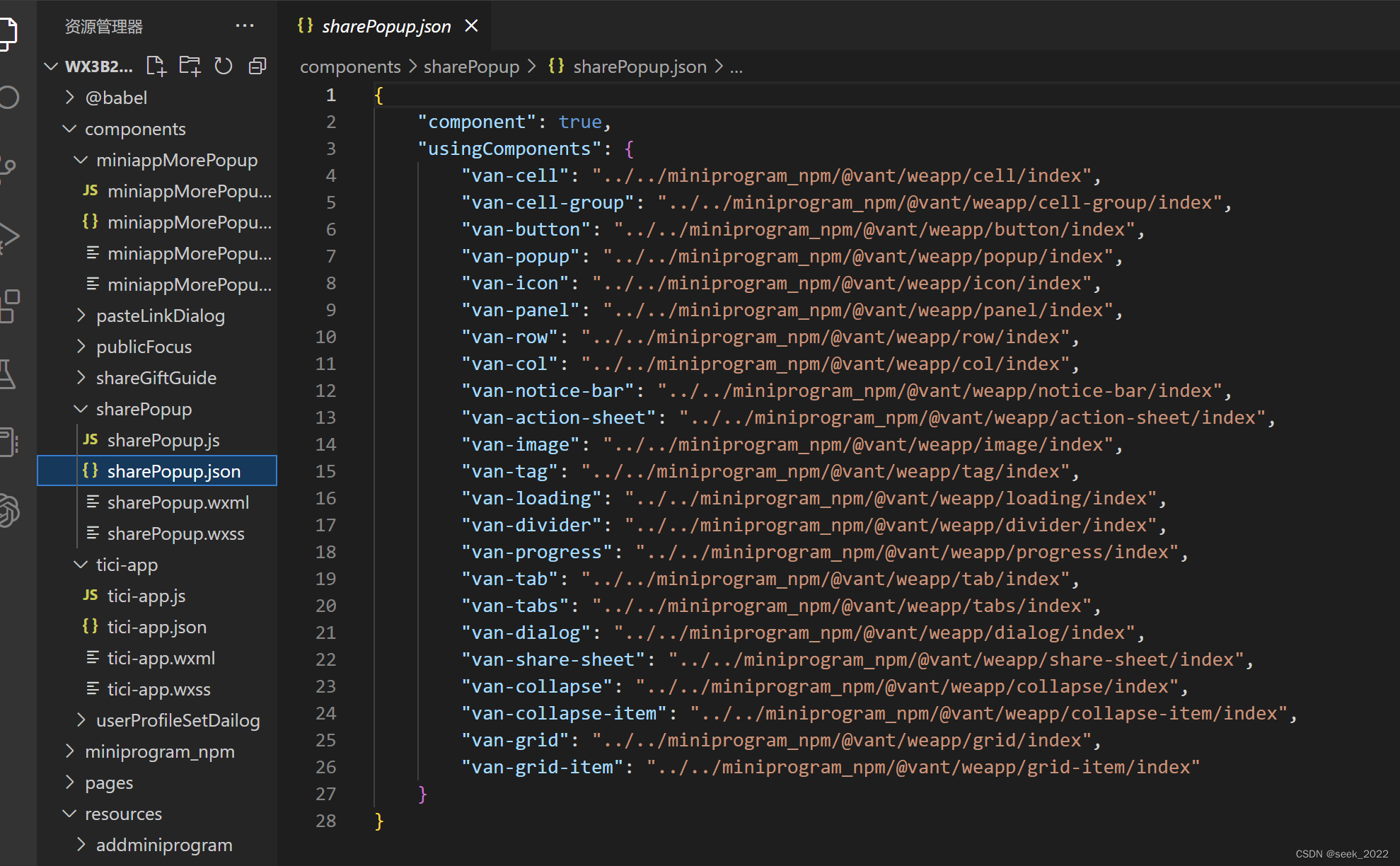
微信小程序反编译方法分享
文章目录一、前言二、准备工作(一)安装Nodejs(二)解密和逆向工具三、小程序缓存文件解密(一)定位小程序缓存路径(二)源码解密(三)源码反编译四、小结一、前言…...
有了这些接口测试用例+工具,测试效率想不提升都难
写在前面:在日常开发过程中,有人做前端开发,有人负责后端开发。接口的主要作用就是连接前后台。但是,由于前端和后端开发的速度可能不一样,尤其是后端开发好了,但前端还未开发。这种时候我们需要做接口测试…...
麒麟 arm架构安装nginx
目录 1、下载nginx安装包并解压 在线安装: 离线安装: 上传nginx安装包(下载地址:https://nginx.org/download/nginx-1.20.2.tar.gz)到指定目录 2、安装系统相关依赖软件、组件包 1、上传或者下载对应的组件包 2、安…...

logrotate失效的排查---selinux开启状态拦截问题及解决方法
首先测试环境selinux 处于关闭状态 disable # getenforce disable重新开启selinux配置与生产环境一致 [rootlocal]# cat /etc/selinux/config # This file controls the state of SELinux on the system. # SELINUX can take one of these three values: # enforcing - S…...

Allegro使用总结-查看Layout基本操作:
好久没用CSDN写过笔记了,没想到无意间打开,编辑器更新啦!以前巨难用的“富文本编辑器”终于改观了😭变的好像语雀,うれしい1. 视图/画面操作a. 画面缩放(Zoom):F11/F12 或 鼠标滚轮b…...

cmd del命令笔记
使用 /s 删除文件夹下所有的 del /s sub # 删除目录下所有文件,这个目录不会删除 /p 确认提示 /q 静默模式,不会提示要不要删除 如过和/p同时使用,那么不提示 /a 根据属性删除,a是attribute的意思 del /a:r 01.jpg # 01.jp…...
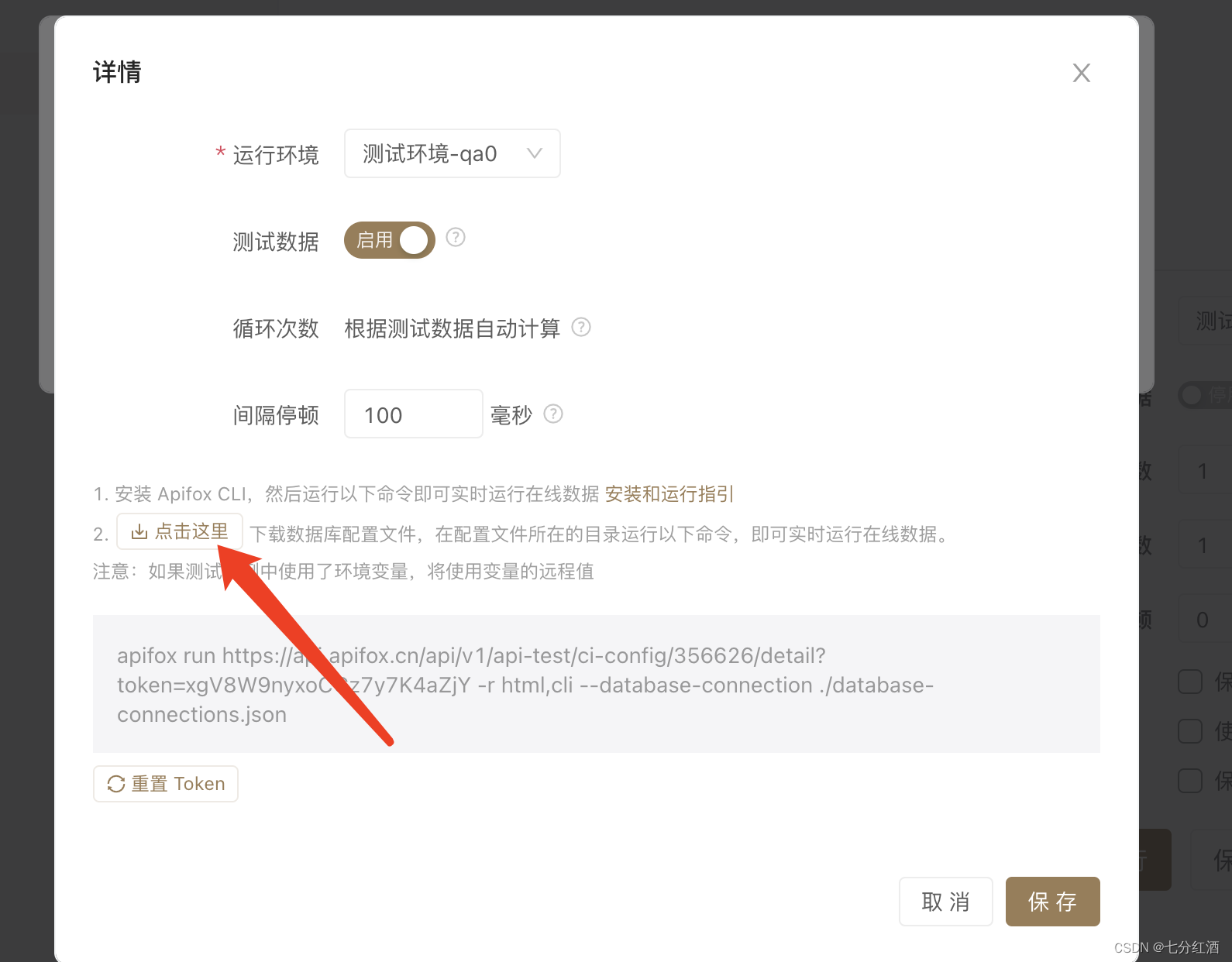
apifox持续集成+java+企微机器人+xxljob定时推送
总览: apifox做接口测试后,把用例合并组装成测试套件,然后apifox-cli通过终端命令实现把套件执行后,输出本地文件的测试报告html或json。本地解析后拿到有用的解决通过定时执行推送到企微群里。 然后把html一起推到群里。 这个…...
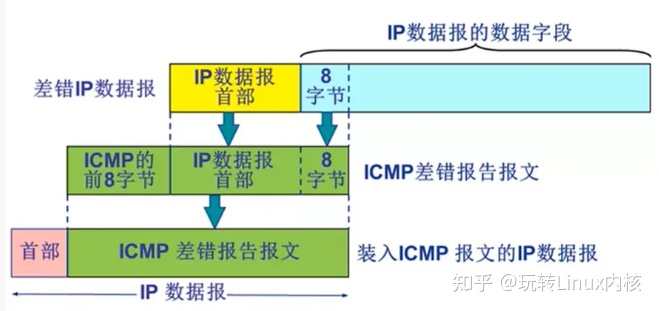
盘点Linux内核网络知识100道题,这篇就够了
计算机网络模型 1、五层因特网协议栈和七层OSI(Open System Interconnections)参考模型分别是什么? 5层:应用层、传输层、网络层、数据链路层、物理层 7层:应用层、表示层、会话层、传输层、网络层、数据链路层、物理…...

数据库敏感字段脱敏
文章目录什么是脱敏脱敏后带来什么问题解决方案一解决方案二具体实施方案一方案二存量数据处理什么是脱敏 如果你有申请过一些软件资质,应该会被要求敏感数据进行加密,比如密码不能明文,用户的手机号,身份证信息,银行…...
--熟悉skynet(网络))
skynet 游戏服务器探索(1)--熟悉skynet(网络)
因为做游戏服务器开发,大多数都跟脚本打交道,要么是lua,要么是python,要么是php,方便热更新的只有lua与php, php相关的游戏服务器开发,参考我另外的文章https://blog.csdn.net/guoyilongedu/article/details/121049511lua脚本相关的ÿ…...

select、poll、epoll
select、poll、epoll select int select(int nfds, fd_set *readfds, fd_set *writefds, fd_set *exceptfds, struct timeval *timeout); int nfds:被select管理的文件描述符的个数,最大描述符编号1fd_set *readfds:读文件描述符集合fd_se…...

rollup的基本使用 基本配置与处理各种文件
rollup rollup是一个javascript的模块化打包工具 可以帮助我们编译小的代码到一个大的负载的代码中 比如一个库或者一个应用 rollup与webpack的区别 rollup主要针对ES Module进行打包 另外webpack通常可以通过各种loader处理各种各样的文件 以及处理他们的依赖关系 rollup更多…...

ubuntu-debian系-redhat系
debian系 包类型:.deb包 本地安装包安装工具:dpkg 本地包管理命令:dpkg -i package 安装包 dpkg -r package 卸载包 dpkg -l package 查看已安装包 远程安装包安装工具:apt / apt-get 远程包管理命令:apt-get apt-cac…...
Altium Designer 18中原理图DRC编译和PCB DRC检查-AD DRC
一、原理图编译 原理图检查的主要内容有: 1、元件位号冲突。也即多个元件编号相同,例如两个电容在原理图中都被命名为C2,显然肯定是无法生成PCB的。 2、网络悬浮。也即网络标号没有附着在电气走线上,一般这种是人操作失误&…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
