归并排序——“数据结构与算法”
各位CSDN的uu们好呀,今天,小雅兰的内容仍然是数据结构与算法专栏的排序呀,下面,让我们进入归并排序的世界吧!!!
归并排序
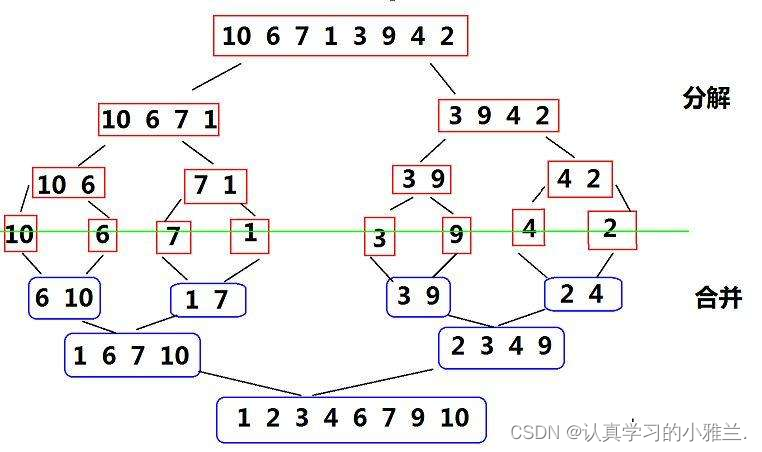
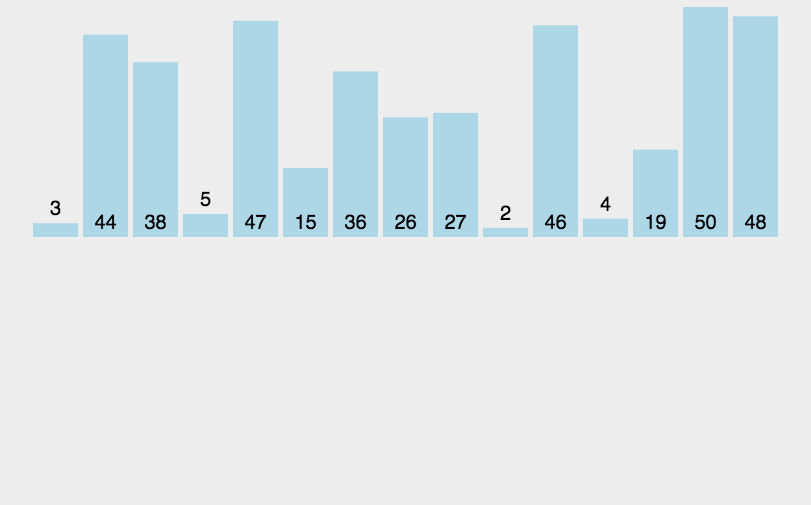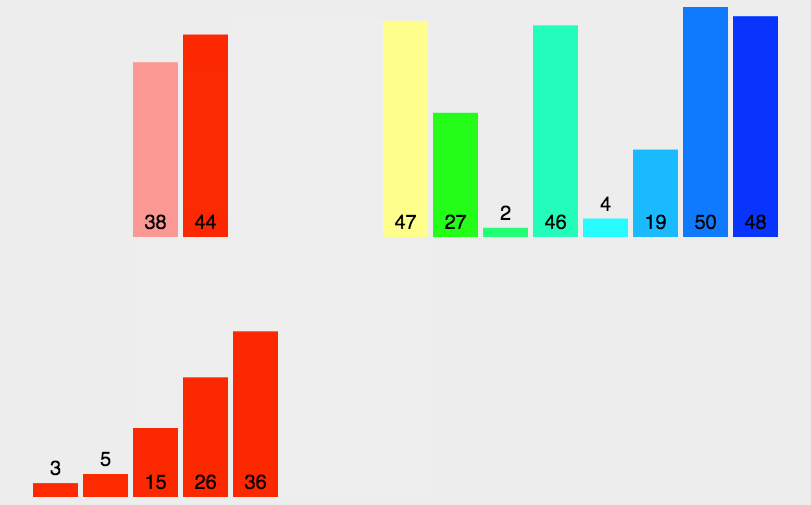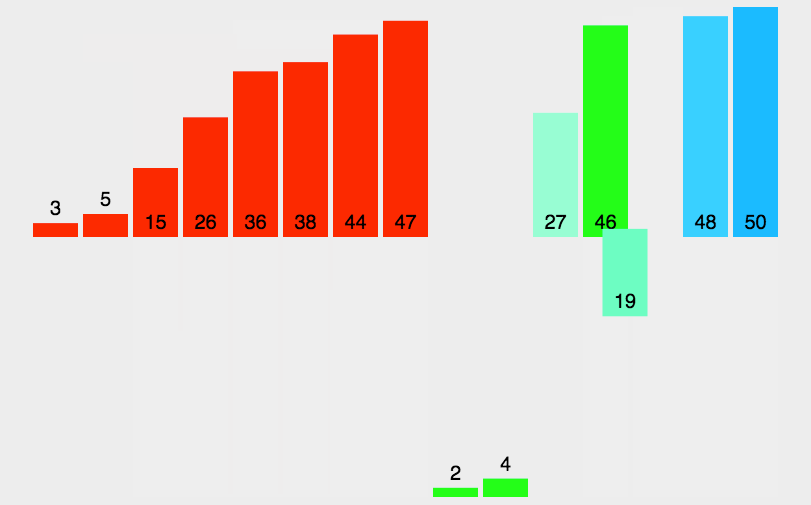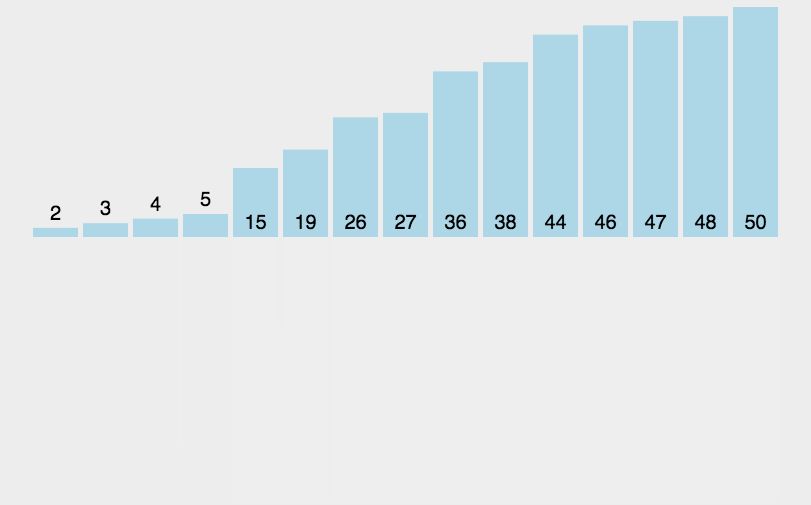
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
void _MergeSort(int* a, int begin, int end, int* tmp) {if (begin >= end){return;}int mid = (begin + end) / 2;//[begin,mid] [mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//归并两个区间int begin1 = begin;int begin2 = mid + 1;int end1 = mid;int end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } //归并排序 void MergeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp); }
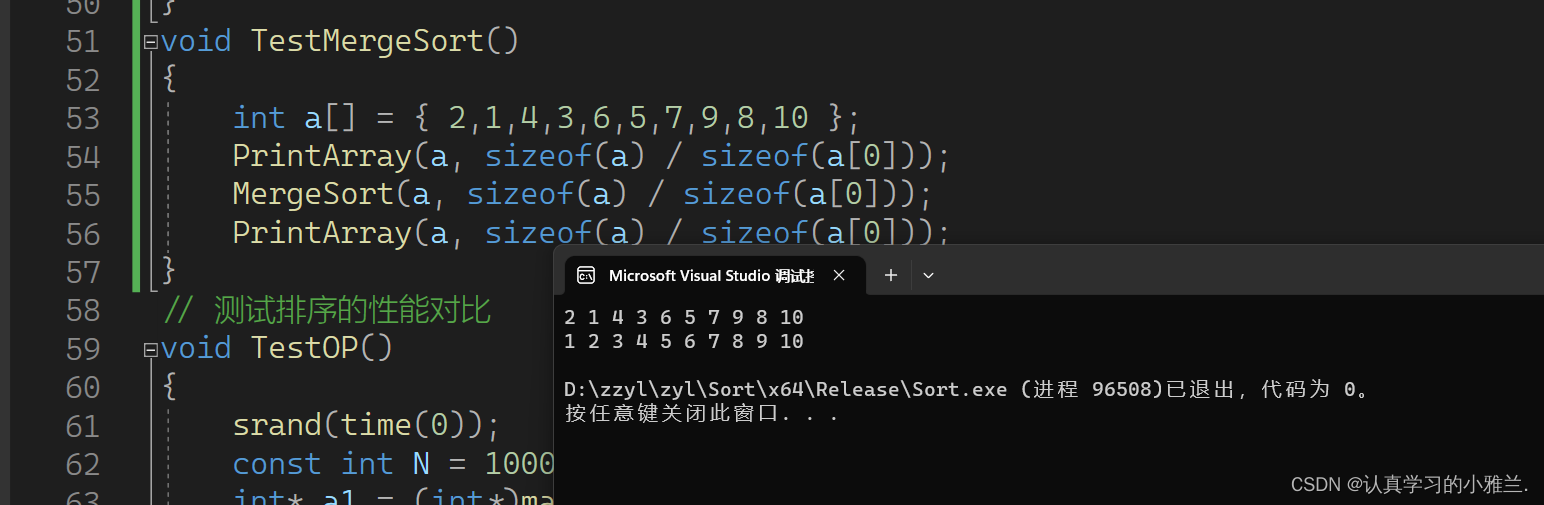
测试一下归并排序:
void TestMergeSort()
{
int a[] = { 2,1,4,3,6,5,7,9,8,10 };
PrintArray(a, sizeof(a) / sizeof(a[0]));
MergeSort(a, sizeof(a) / sizeof(a[0]));
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
归并排序非递归
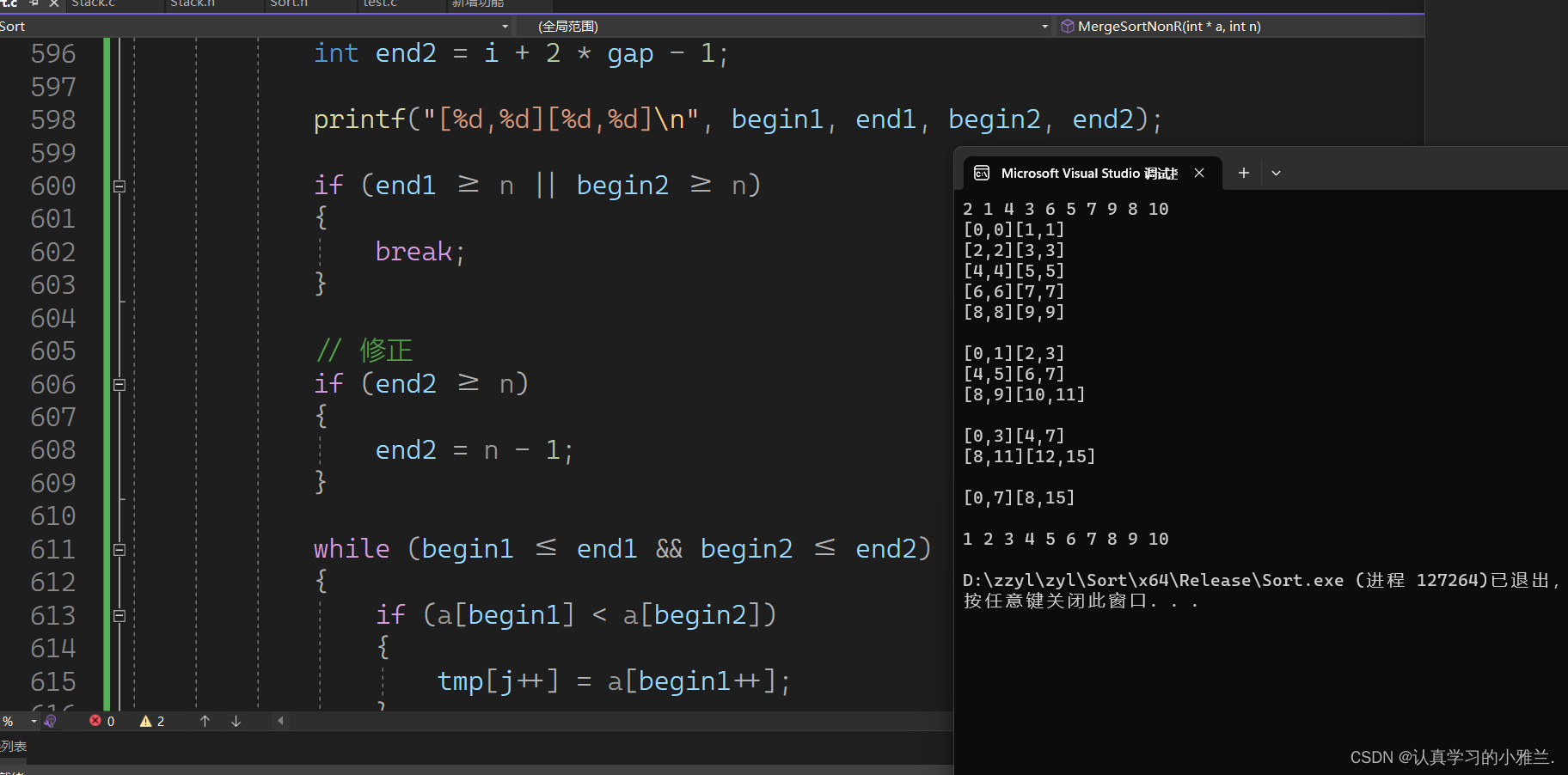
void MergeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc失败!!!");return;}int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += gap){//每组的合并数据int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}}memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp); }但是这个代码是有非常严重的越界问题的,只有有2的次方的数据的时候,才不会越界!!!
小雅兰在这里打印几组数据看得更加清楚:
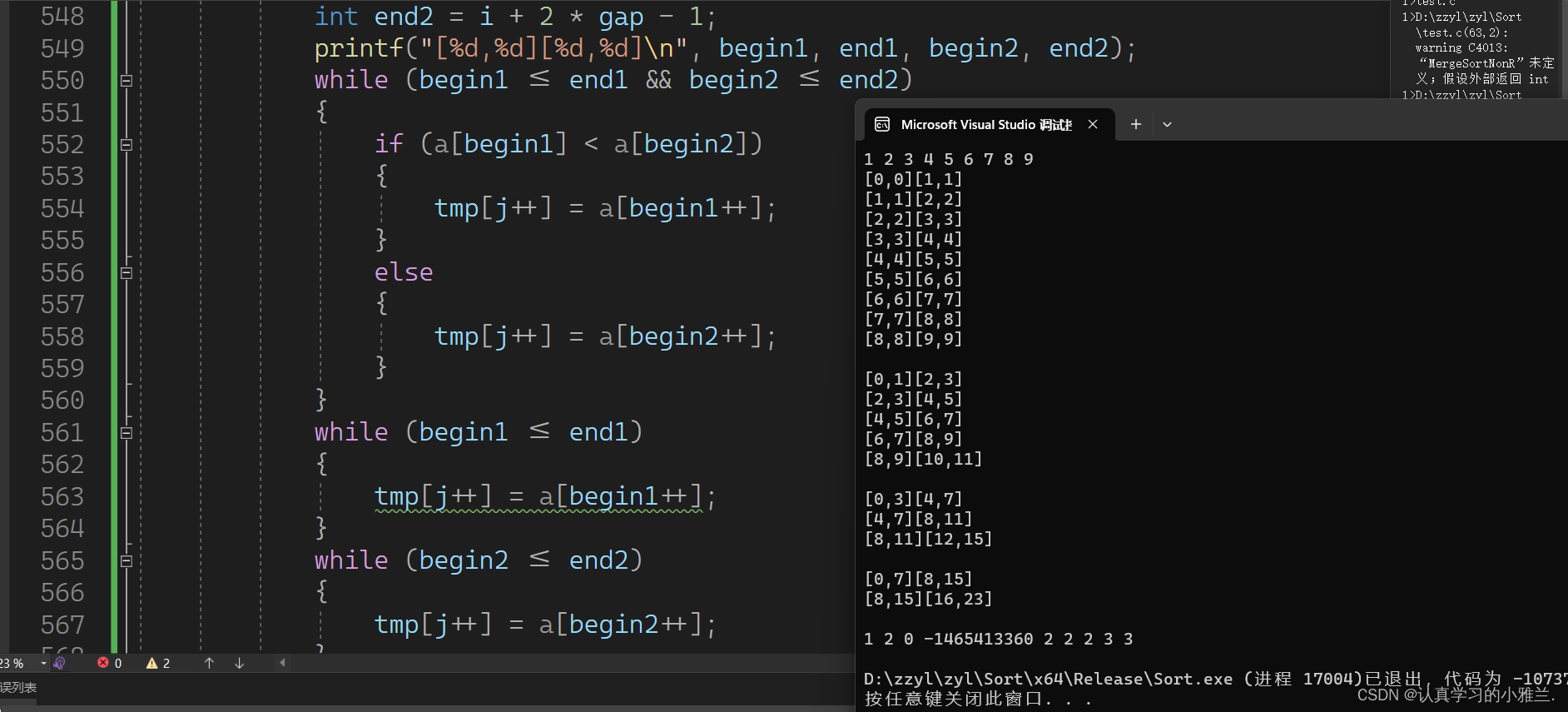
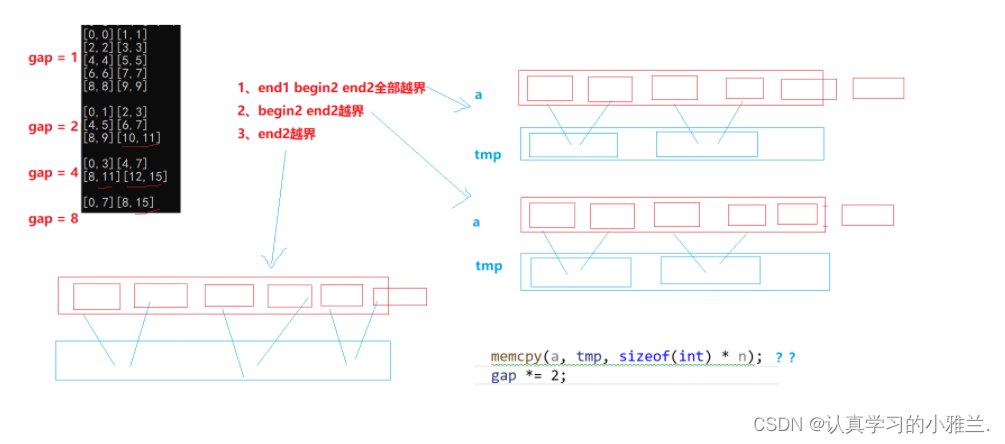
void MergeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc失败!!!");return;}// 1 2 4 ....int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){// 每组的合并数据int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);if (end1 >= n || begin2 >= n){break;}// 修正if (end2 >= n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}// 归并一组,拷贝一组memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}printf("\n");gap *= 2;}free(tmp); }这样修正一下就可以啦!!!
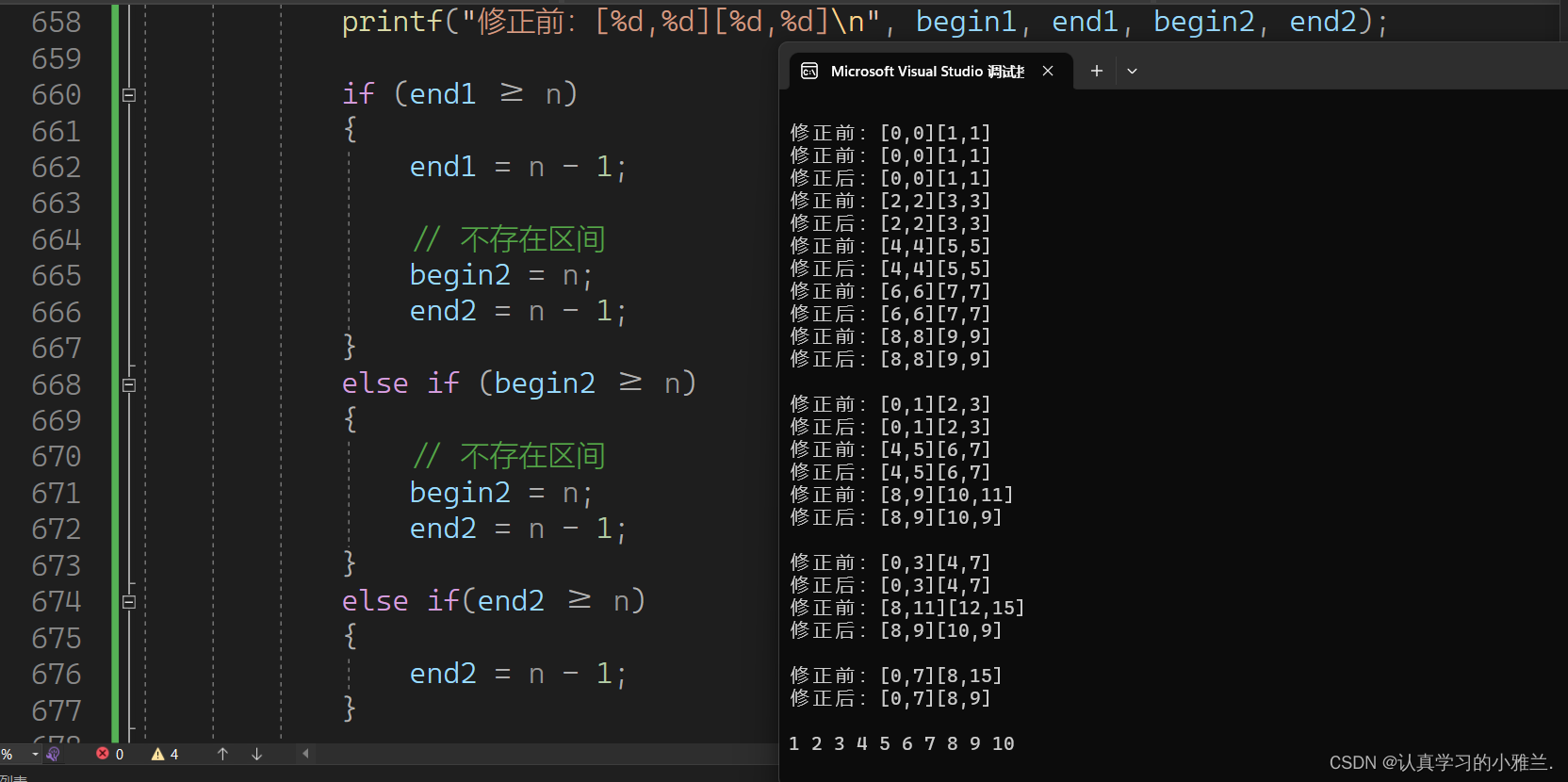
这个越界问题还有第二种解决方案:
void MergeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);// 1 2 4 ....int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){// 每组的合并数据int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;printf("修正前:[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);if (end1 >= n){end1 = n - 1;// 不存在区间begin2 = n;end2 = n - 1;}else if (begin2 >= n){// 不存在区间begin2 = n;end2 = n - 1;}else if(end2 >= n){end2 = n - 1;}printf("修正后:[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}}printf("\n");memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp); }
测试各种排序
// 测试排序的性能对比 void TestOP() {srand(time(0));const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7); }
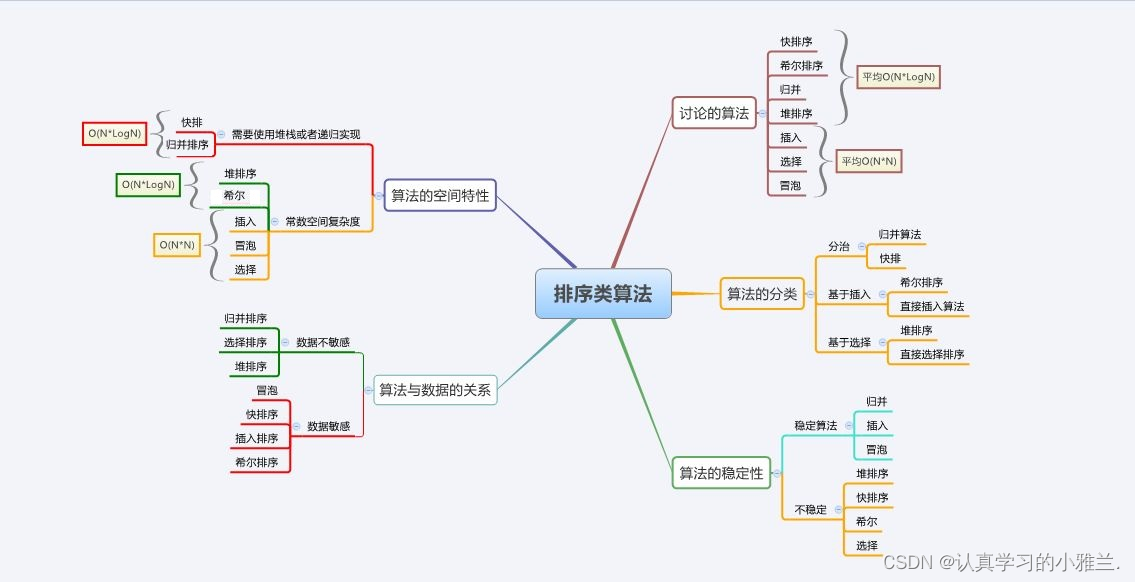

所有排序源代码:
Sort.h的内容:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<stdbool.h>
#include<string.h>
void PrintArray(int* a, int n);
// 直接插入排序
void InsertSort(int* a, int n);// 希尔排序
void ShellSort(int* a, int n);// 直接选择排序
void SelectSort(int* a, int n);// 堆排序
void AdjustDown(int* a, int n, int root);
void HeapSort(int* a, int n);// 冒泡排序
void BubbleSort(int* a, int n);//快速排序
int PartSort1(int* a, int left, int right);
int PartSort2(int* a, int left, int right);
int PartSort3(int* a, int left, int right);
void QuickSort(int* a, int begin, int end);void QuickSortNonR(int* a, int begin, int end);
//归并排序
void MergeSort(int* a, int n);void MergeSortNonR(int* a, int n);
Sort.c的内容:
#include"Sort.h"
#include"Stack.h"
void PrintArray(int* a, int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
//直接插入排序
void InsertSort(int* a, int n)
{
int i = 0;
for (i = 1; i < n; i++)
{
int end = i - 1;
int tmp = a[i];
while (end >= 0)
{
//插入的数据比原来的数据小
if (a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
//希尔排序
void ShellSort(int* a, int n)
{
//1.gap>1,预排序
//2.gap==1,直接插入排序
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
//+1可以保证最后一次一定是1
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
//冒泡排序
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; j++)
{
bool exchange = false;
for (int i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
int tmp = a[i];
a[i] = a[i - 1];
a[i - 1] = tmp;
exchange = true;
}
}
if (exchange == false)
{
break;
}
}
}
void Swap(int* a1, int* a2)
{
int tmp = *a1;
*a1 = *a2;
*a2 = tmp;
}//直接选择排序
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int maxi = begin;
int mini = begin;
for (int i = begin; i <= end; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[begin], &a[mini]);
//如果maxi和begin重叠,修正一下即可
if (begin ==maxi)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
++begin;
--end;
}
}//向下调整算法
void AdjustDown(int* a, int n, int parent)
{
//默认左孩子小
int child = parent * 2 + 1;
while (child < n)//孩子在数组范围内
{
//选出左右孩子中大的那一个
//有可能假设错了
//左孩子不存在,一定没有右孩子——完全二叉树
//左孩子存在,有可能没有右孩子
if (child + 1 < n && a[child + 1] > a[child])
// 右孩子存在 右孩子>左孩子
//不能这么写 if (a[child + 1] > a[chid] && child + 1 < n )
//这样写会有越界的风险 因为是先访问了数组中的元素 再去比较右孩子是否存在
{
++child;
}
//child就是大的那个孩子
//不关心到底是左孩子还是右孩子
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;//默认又算的是左孩子
}
else
{
break;
}}
}
//堆排序
void HeapSort(int* a, int n)
{
//建堆——向下调整建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//升序——建大堆
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}//三数取中
int GetMidIndex(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return right;
}
else
{
return left;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return right;
}
else
{
return left;
}
}
}
// hoare
// [left, right]
int PartSort1(int* a, int left, int right)
{
int midi = GetMidIndex(a, left, right);
Swap(&a[left], &a[midi]);int keyi = left;
while (left < right)
{
// 右边找小
while (left < right && a[right] >= a[keyi])
{
--right;
}// 左边找大
while (left < right && a[left] <= a[keyi])
{
++left;
}Swap(&a[left], &a[right]);
}Swap(&a[keyi], &a[left]);
return left;
}
挖坑法
[left, right]
//int PartSort2(int* a, int left, int right)
//{
// int midi = GetMidIndex(a, left, right);
// Swap(&a[left], &a[midi]);
//
// int key = a[left];
// int hole = left;
// while (left < right)
// {
// // 右边找小
// while (left < right && a[right] >= key)
// {
// --right;
// }
//
// a[hole] = a[right];
// hole = right;
//
// // 左边找大
// while (left < right && a[left] <= key)
// {
// ++left;
// }
//
// a[hole] = a[left];
// hole = left;
// }
//
// a[hole] = key;
//
// return hole;
//}
//
前后指针法
[left, right]
//int PartSort3(int* a, int left, int right)
//{
// int midi = GetMidIndex(a, left, right);
// Swap(&a[left], &a[midi]);
//
// int prev = left;
// int cur = left + 1;
// int keyi = left;
// while (cur <= right)
// {
// if (a[cur] < a[keyi] && ++prev != cur)
// {
// Swap(&a[prev], &a[cur]);
// }
//
// ++cur;
// }
//
// Swap(&a[prev], &a[keyi]);
// keyi = prev;
// return keyi;
//}
//快速排序
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = PartSort1(a, begin, end);
//[begin,keyi-1] keyi [keyi+1,end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
//快速排序非递归
void QuickSortNonR(int* a, int begin, int end)
{
Stack st;
StackInit(&st);
StackPush(&st, end);
StackPush(&st, begin);while (!StackEmpty(&st))
{
int left = StackTop(&st);
StackPop(&st);int right = StackTop(&st);
StackPop(&st);int keyi = PartSort1(a, left, right);
// [left, keyi-1] keyi [keyi+1, right]
if (keyi + 1 < right)
{
StackPush(&st, right);
StackPush(&st, keyi + 1);
}if (left < keyi - 1)
{
StackPush(&st, keyi - 1);
StackPush(&st, left);
}
}StackDestroy(&st);
}
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
//[begin,mid] [mid+1,end]
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
//归并两个区间
int begin1 = begin;
int begin2 = mid + 1;
int end1 = mid;
int end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
//归并排序
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc失败!!!");
return;
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}//归并排序非递归
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);// 1 2 4 ....
int gap = 1;
while (gap < n)
{
int j = 0;
for (int i = 0; i < n; i += 2 * gap)
{
// 每组的合并数据
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;printf("修正前:[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
if (end1 >= n)
{
end1 = n - 1;// 不存在区间
begin2 = n;
end2 = n - 1;
}
else if (begin2 >= n)
{
// 不存在区间
begin2 = n;
end2 = n - 1;
}
else if(end2 >= n)
{
end2 = n - 1;
}printf("修正后:[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
printf("\n");memcpy(a, tmp, sizeof(int) * n);
gap *= 2;
}free(tmp);
}
//void MergeSortNonR(int* a, int n)
//{
// int* tmp = (int*)malloc(sizeof(int) * n);
// if (tmp == NULL)
// {
// perror("malloc失败!!!");
// return;
// }
// // 1 2 4 ....
// int gap = 1;
// while (gap < n)
// {
// int j = 0;
// for (int i = 0; i < n; i += 2 * gap)
// {
// // 每组的合并数据
// int begin1 = i;
// int end1 = i + gap - 1;
// int begin2 = i + gap;
// int end2 = i + 2 * gap - 1;
//
// printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
//
// if (end1 >= n || begin2 >= n)
// {
// break;
// }
//
// // 修正
// if (end2 >= n)
// {
// end2 = n - 1;
// }
//
// while (begin1 <= end1 && begin2 <= end2)
// {
// if (a[begin1] < a[begin2])
// {
// tmp[j++] = a[begin1++];
// }
// else
// {
// tmp[j++] = a[begin2++];
// }
// }
//
// while (begin1 <= end1)
// {
// tmp[j++] = a[begin1++];
// }
//
// while (begin2 <= end2)
// {
// tmp[j++] = a[begin2++];
// }
//
// // 归并一组,拷贝一组
// memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
// }
// printf("\n");
// gap *= 2;
// }
// free(tmp);
//}
Leetcode每日一题——“912.排序数组”
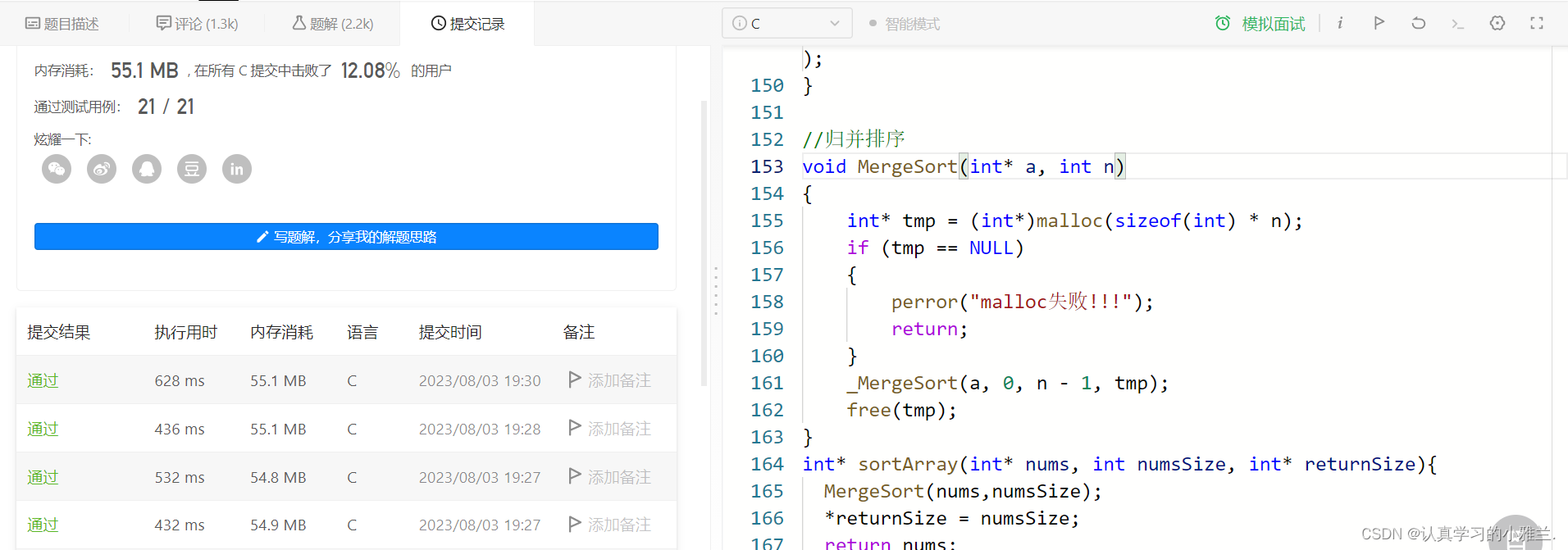
在leetcode上面有一道题,可以用各种排序测试可不可以通过:
小雅兰在这边尝试了一下归并排序,很轻松就过啦!!!
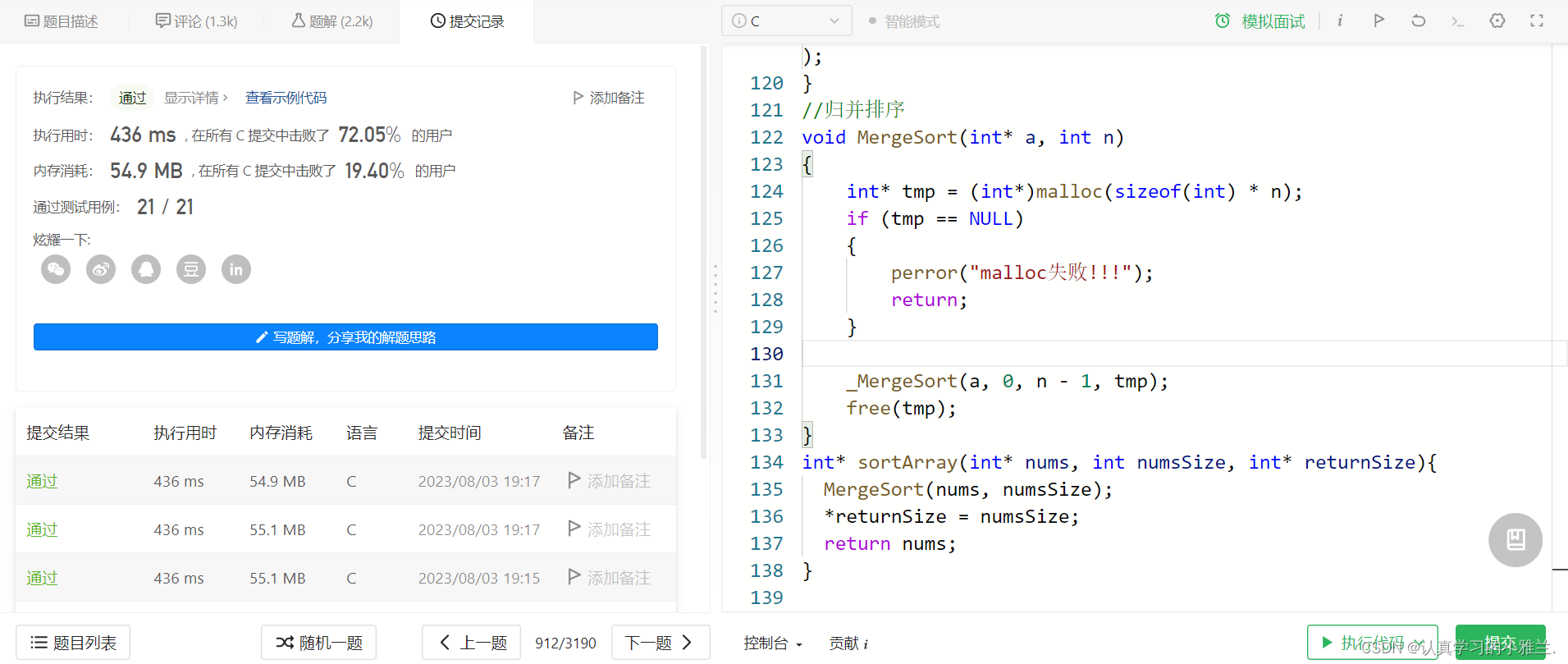
void _MergeSort(int* a, int begin, int end, int* tmp) {if (begin >= end){return;}int mid = (begin + end) / 2;//[begin,mid] [mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//归并两个区间int begin1 = begin;int begin2 = mid + 1;int end1 = mid;int end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } //归并排序 void MergeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc失败!!!");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp); } int* sortArray(int* nums, int numsSize, int* returnSize){MergeSort(nums, numsSize);*returnSize = numsSize;return nums; }
还可以这样写,是进行了小区间优化的版本,相对来说好一点,但leetcode上面测试不了此效果:
//直接插入排序 void InsertSort(int* a, int n) {int i = 0;for (i = 1; i < n; i++){int end = i - 1;int tmp = a[i];while (end >= 0){//插入的数据比原来的数据小if (a[end] > tmp){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;} } void _MergeSort(int* a, int begin, int end, int* tmp) {if (begin >= end){return;}//小区间优化if(end-begin+1<10){InsertSort(a+begin,end-begin+1);return;}int mid = (begin + end) / 2;//[begin,mid] [mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//归并两个区间int begin1 = begin;int begin2 = mid + 1;int end1 = mid;int end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); }//归并排序 void MergeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc失败!!!");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp); } int* sortArray(int* nums, int numsSize, int* returnSize){MergeSort(nums,numsSize);*returnSize = numsSize;return nums; }
但是这道题,用直接插入排序、冒泡排序这种排序就过不了了,会提示:超出时间限制
遗憾的是:快速排序也没过,小雅兰反复测试了好多遍
好啦,小雅兰今天的归并排序的内容就到这里啦,还要继续加油!!!

相关文章:

归并排序——“数据结构与算法”
各位CSDN的uu们好呀,今天,小雅兰的内容仍然是数据结构与算法专栏的排序呀,下面,让我们进入归并排序的世界吧!!! 归并排序 归并排序(MERGE-SORT)是建立在归并操作上的一种…...

C语言笔试题训练【第一天】
目录 第一题 第二题 第三题 第四题 第五题 大家好,我是纪宁。 从今天开始博主会日更一些经典的C语言笔试题,持续20天左右。题目类型为5道选择题加2道编程题,希望能和大家一起进步。 第一题 1.读程序,下面程序正确的输出是&…...

计算语言模型计算每秒钟生成的token数量it/s
在 main() 函数的stream循环中,我们可以计算每秒钟生成的token数量,然后输出 it/s。在流式生成过程中,我们可以使用Python的time模块来计算速度。在测试时,生成速度会受到多个因素的影响,包括设备性能、模型大小、输入…...

Clickhouse调研
1、独立组件个数(按进程) 默认情况下是1个;如果需要使用副本机制,需要依赖zookeeper;如果需要监控功能,还得依赖第三方监控系统。 2、单机部署 很好的支持单机运行,并且单机情况下查询入库性能不错(通过其提供的示例数据进行体验)。 3、窗口函数 Clickhouse没有显示…...

02.Redis实现添加缓存功能
学习目标: 提示:学习如何利用Redis实现添加缓存功能 学习产出: 流程图 1. 准备pom环境 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId&g…...
【1.2】Java微服务:SpringCloud概论
✅作者简介:大家好,我是 Meteors., 向往着更加简洁高效的代码写法与编程方式,持续分享Java技术内容。 🍎个人主页:Meteors.的博客 💞当前专栏: 微服务 ✨特色专栏: 知识分享 &#x…...
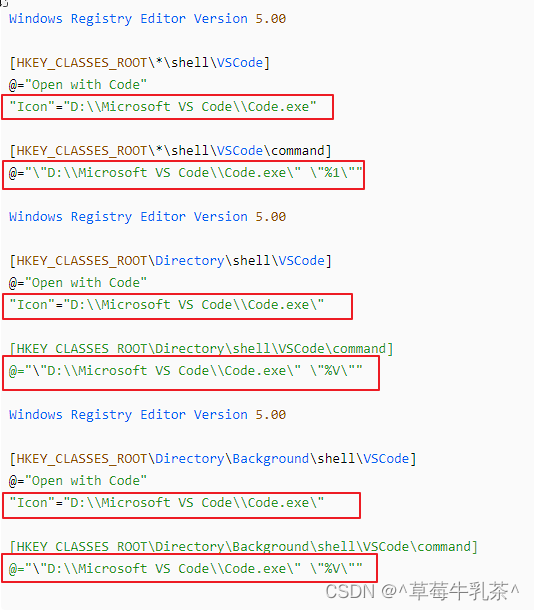
右键文件夹 ------- 打开 vscode的方法
1、右键vscode点击属性 2、这是地址栏,一会复制即可 3、新建一个txt文件,将这个复制进去 Windows Registry Editor Version 5.00[HKEY_CLASSES_ROOT\*\shell\VSCode] "Open with Code" "Icon""D:\\Microsoft VS Code\\Code.exe"[HKE…...

小程序原生实现左右锚点联动
效果 wxml <view classbox><scroll-view scroll-y scroll-with-animation style"width:25%"><view classnav><view wx:for"{{navList}}" wx:keyindex class"title {{index active ?select:}}"data-index{{index}} bin…...
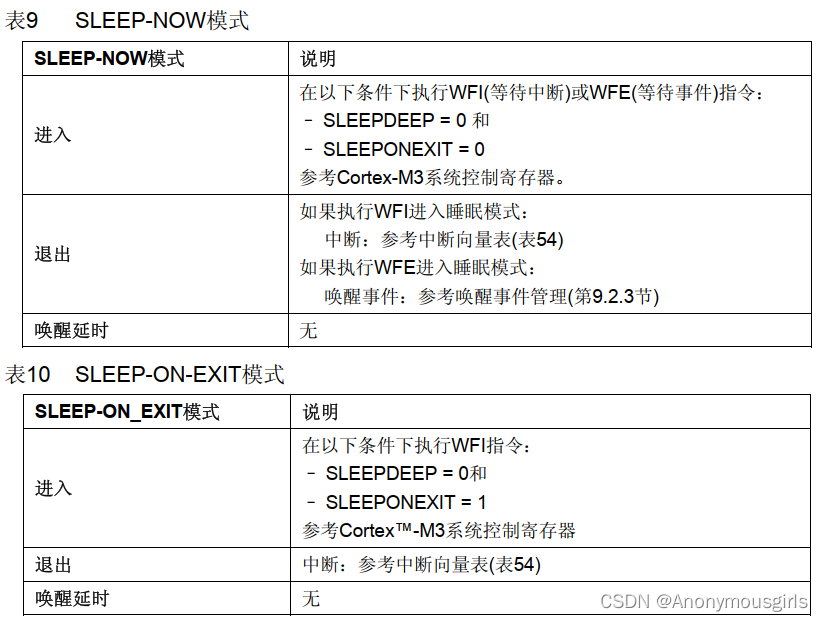
STM32 低功耗-睡眠模式
STM32 睡眠模式 文章目录 STM32 睡眠模式第1章 低功耗模式简介第2章 睡眠模式简介2.1 进入睡眠模式2.1 退出睡眠模式 第3章 睡眠模式代码示例总结 第1章 低功耗模式简介 在 STM32 的正常工作中,具有四种工作模式:运行、睡眠、停止和待机模式。 在系统或…...
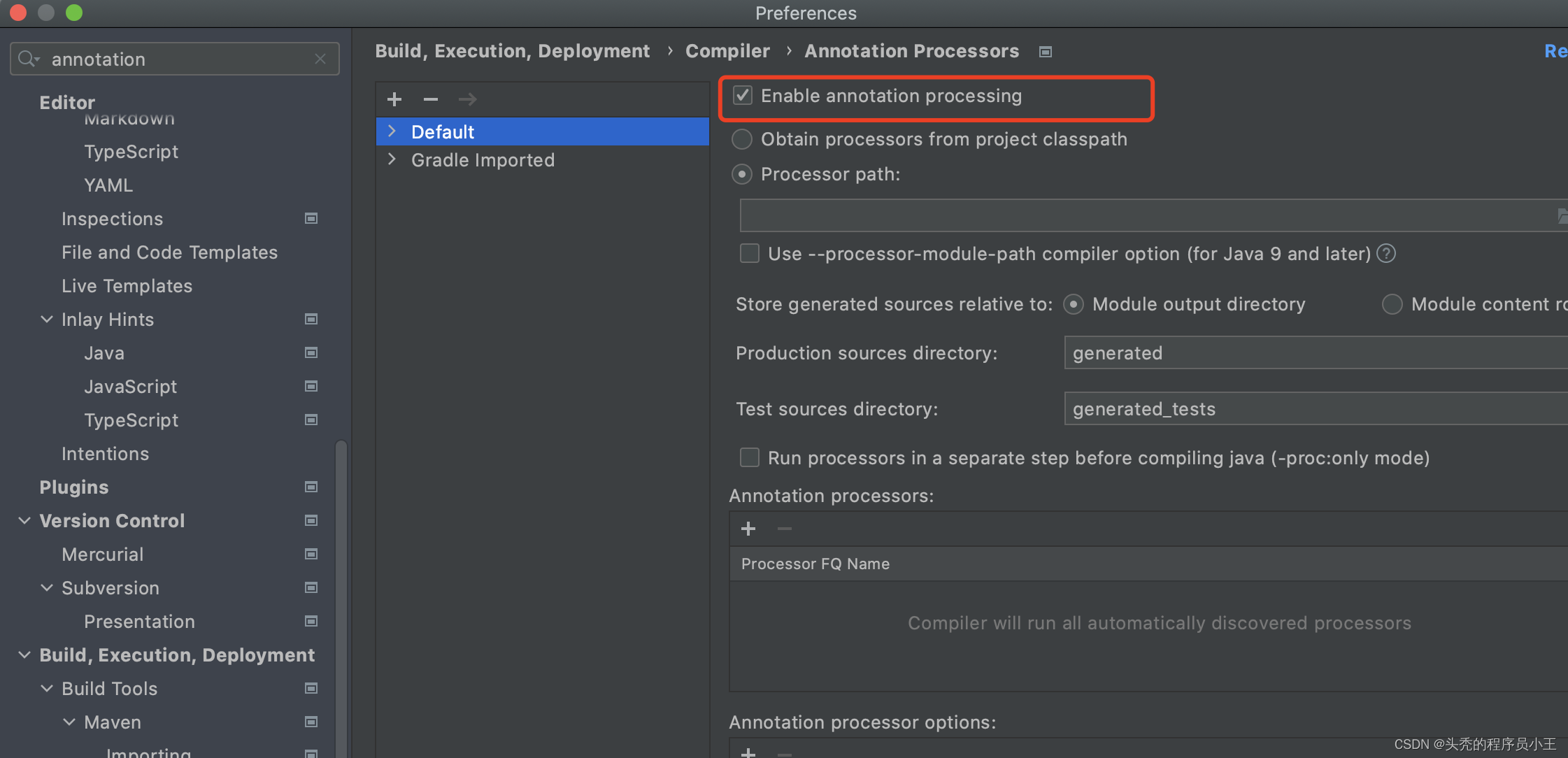
IDEA用Gradle构建项目时,lombok插件无效的解决办法
Lombok 可用来帮助开发人员消除 Java 的重复代码,尤其是对于简单的 Java 对象(POJO),比如说getter/setter/toString等方法的编写。它通过注解实现这一目的。 正确使用姿势 一、安装Lombok插件 菜单栏File -> Settings ->…...
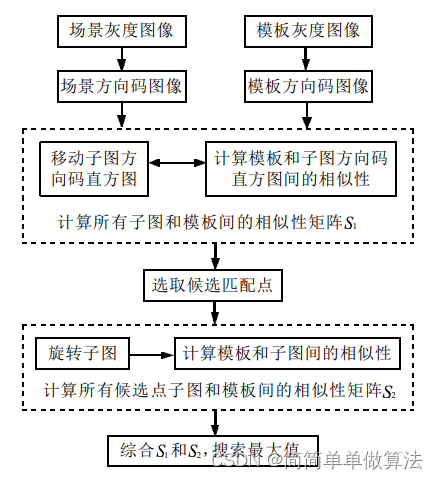
基于方向编码的模板匹配算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 MATLAB2022a 3.部分核心程序 ........................................................................... %选择移动个…...
shell centos 7 一键部署 KVM软件脚本
这个脚本有限地方还需要完善下 设计思路: 1、创建检查内核函数 check_kernel() 2、创建升级内核函数 update_kernel() 3、创建检查是否支持虚拟化函数 check_virtual() 4、创建检查操作系统函数 check_system() 5、创建检查网络函数 check_network() 6…...
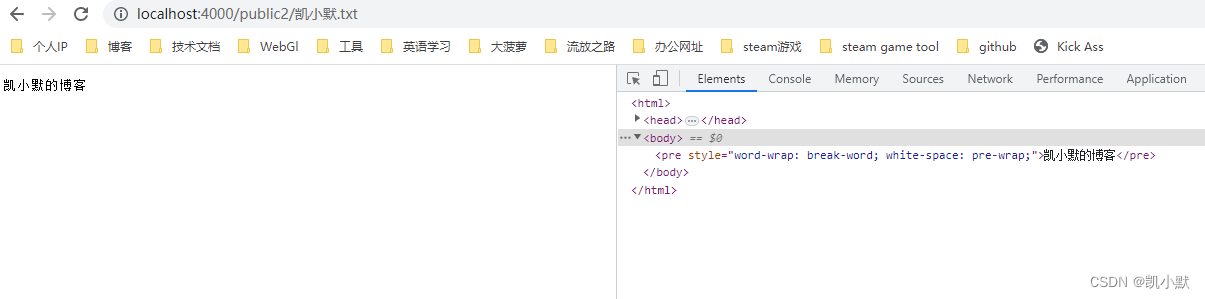
64 # 实现一个 http-server
准备工作 上一节实现了通过 commander 的配置获取到用户的参数,下面完成借用 promise 写成类的方法一节没有完成的任务,实现一个 http-server,https://www.npmjs.com/package/http-server,http-server 是一个简单的零配置命令行静…...
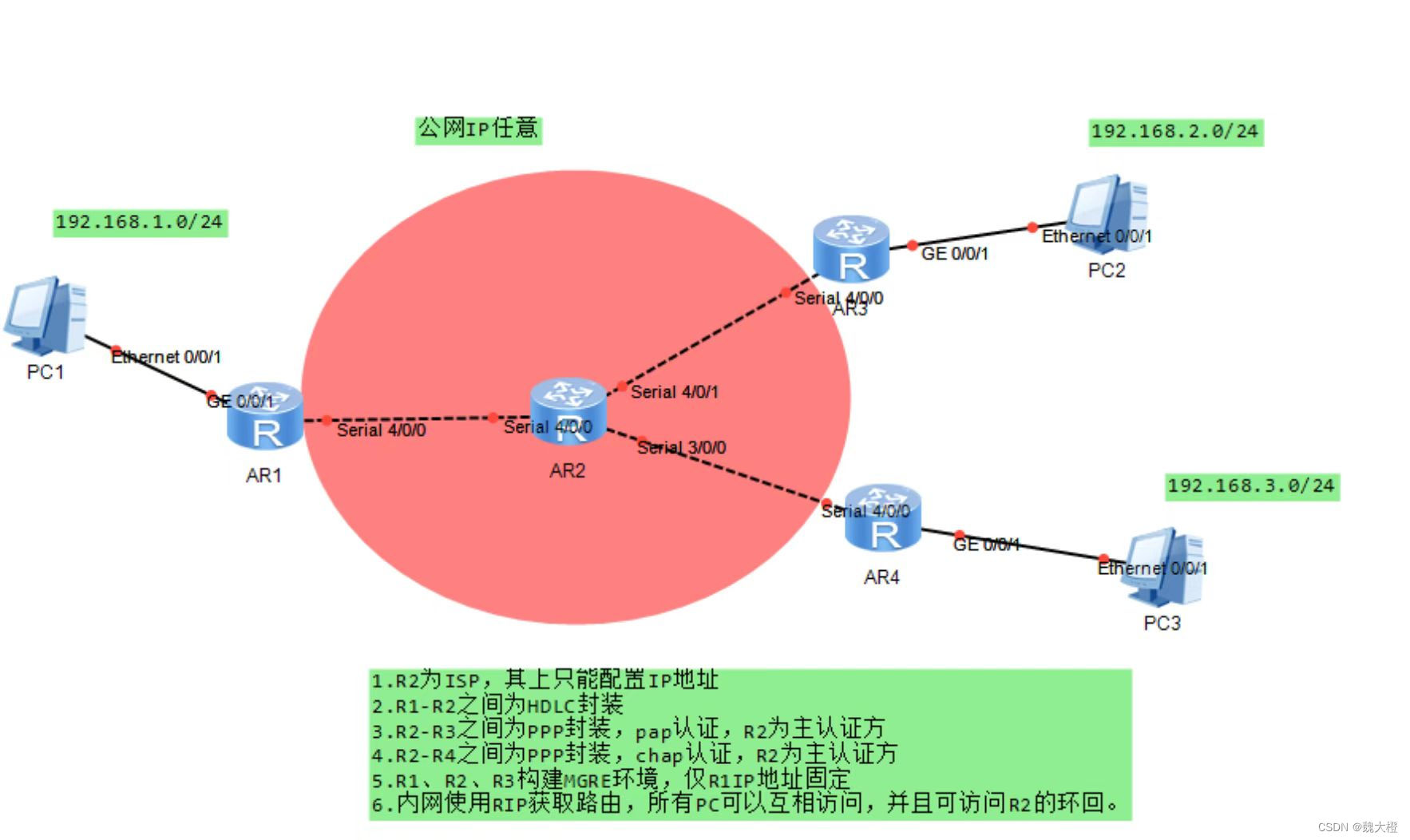
HCIP作业3
题目 配置IP地址 R1 [r1]int g0/0/1 [r1-GigabitEthernet0/0/1]ip add 192.168.1.1 24 [r1-Serial4/0/0]ip add 12.1.1.1 24 R2 [r2]int s4/0/0 [r2-Serial4/0/0]ip add 12.1.1.2 24 [r2-Serial4/0/0]int s4/0/1 [r2-Serial4/0/1]ip add 32.1.1.1 24 [r2-Serial4/0/1]in…...

【测试学习三】软件测试的生命周期 BUG的相关知识
目录 一、软件测试的生命周期(重要) 🍑1、软件的生命周期? 🍑2、软件测试的生命周期? 二、关于BUG 🍑1、如何描述与定义一个BUG?(了解) 🍑2…...

git rebase 的坑儿
1 同步远程仓库 git pull --rebase拉取远程分支之后如果没有冲突直接使用 git rebase --continue若有冲突, 解决冲突, 一般是使用当前的更改, 因为传入的更改是你本地的更改 然后使用 git add 提交冲突 此处千万别使用 git commit --amend 最后使用 git rebase --continu…...
SSM(Vue3+ElementPlus+Axios+SSM前后端分离)【四】
文章目录 SSM(Vue3ElementPlusAxiosSSM前后端分离)--基础环境搭建【四】项目介绍项目功能/界面● SSM 整合项目界面 创建表,使用逆向工程生成Bean、XxxMapper 和XxxMapper.xml1. 创建furns_ssm 数据库和furns 表使用MyBatis Generator 逆向工程生成bean mapper 接口…...

iPhone 8 Plus透明屏应用范围详解
iPhone 8 Plus是苹果公司于2017年推出的一款智能手机,它采用了全新的玻璃机身设计,支持无线充电,并且搭载了更强大的A11仿生芯片。 而透明屏则是一种新型的屏幕技术,可以使手机屏幕呈现出透明的效果。 透明屏是一种将屏幕背后的元…...

【前端面试手撕题】instanceof、Array.map、Array.filter、Array.reduce、_objectCreate
FED6 instanceof 描述 请补全JavaScript代码,要求以Boolean的形式返回第一个实例参数是否在第二个函数参数的原型链上。 <!DOCTYPE html> <html><head><meta charset"UTF-8"><style>/* 填写样式 */</style> </h…...

8.物联网操作系统之事件标志组
。事件标志组定义 FreeRTOS事件标志组介绍 FreeRTOS事件标志组工作原理 一。事件标志组定义 信号量信号量只能实现任务与单个事件或任务间的同步。但是某些任务可能会需要与多个事件或任务进行同步,此时就可以使用事件标志组来解决。事件标志组能够实现某个任务与…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...