方差分析||判断数据是否符合正态分布
方差分析练习题
练习学习笔记:
(1)

标准差和标准偏差、均方差是一个东西。标准误差和标准误是一个东西。这两个东西有区别。
(2)单因素方差分析(MATLAB求解)

(3)使用anova1进行单因素方差分析时,要考虑数据是均衡数据还是不均衡数据。所谓均衡就是要求不同的组别内的统计数据个数必须相同,不均衡反之。如果是均衡数据的话,直接在函数里传入要分析的数据就可以了,但如果是不均衡数据的话,还要加入一个参数,这个参数用来给分析的数据贴上标签,告诉计算机每个数据是属于哪个标签的数据。
例如:对于以下单因素不均衡数据进行方差分析
组一(st):82 86 79 83 84 85 86 87
组二(al1):74 82 78 75 76 77
组三(al2):79 79 77 78 82 79
>> strength = [82 86 79 83 84 85 86 87 74 82 78 75 76 77 79 79 77 78 82 79];
>> alloy = {'st','st','st','st','st','st','st','st','al1','al1','al1','al1','al1','al1','al2','al2','al2','al2','al2','al2'};
>> p = anova1(strength,alloy)
(4)探究不同因素的在不同水平的表现是否有显著差异和探究因素对于某一变量是否有显著影响是两个问题
(5)到底是p<0.05还是p<α才是有显著性差异????????是否符合正态分布,判断因素对于一个元是否有显著性影响(判断因素不同水平在同一变量上的数据是否有显著性差异),判断不同因素在同一元上是否有显著性影响,以及判断不同因素在同一元上是否具有交互效应。是否都是通过判断p和α的大小?????我在知乎上看见了一篇非常值得借鉴的文章以及对话,分享给大家
方差分析(ANOVA)分类、应用举例及matlab代码 - 知乎 (zhihu.com)

题目

解答过程
- 进行单因素方差分析:检验四种广告方式下销售量数据是否服从正态分布方差是否相等; 检验四种广告方式下的销售量是否有显著差异(a = 0.01 );若四广告方式下的销售量有显著差异,指出哪些类型的广告效果有显著的不同?
1.1判断四种广告方式下销售量数据是否符合服从正态分布,方差是否相等。
方法一:利用SPSS进行解题

图1

图2
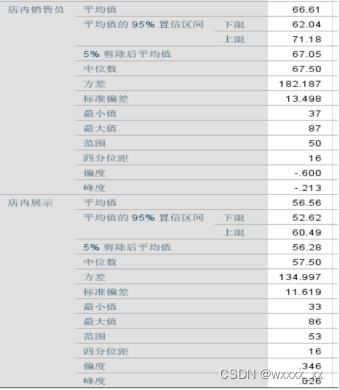
图3
由图1、2、3显示的数据得到,这四种广告形式都服从正态分布,因为显著性都大于α(0.01)。且可看出这四种方式的方差不相等。
方法二:matlab的lillietest()函数
h = 0可以认为数据服从正态分布,h=1则认为不服从正态分布
p >α(0.01)可以认为接受原假设h = 0,则数据服从正态分布
代码:
x=xlsread('表格路径')for i=1:size(x,2)[h,p] = lillietest(x(:,i))end结果:
h1 = 0
p1 = 0.136174630346454
h2 = 0
p2 = 0.413487427029479
h3 = 0
p3 = 0.240288230148084
h4 = 0
p4 = 0.440277544446158
结果表明四种广告方式下销售量的数据都符合正态分布
1.2判断显著差异,使用MATLAB的anova1()函数进行分析
代码如图4
导入表格的数据每一列数据对应以下四种广告
![]()
![]()
图4
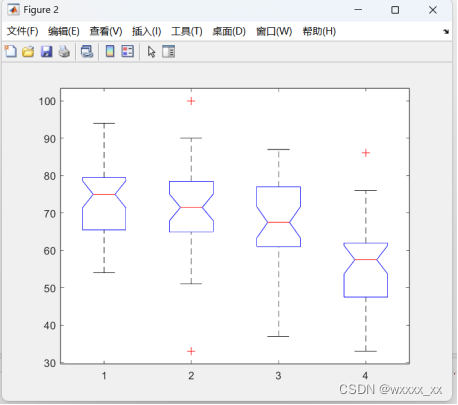
图5
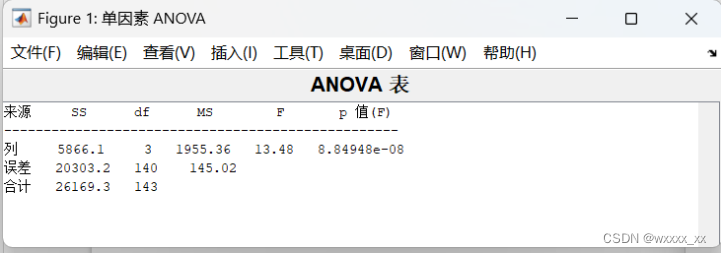
图6

图7

图8
对于anova1()函数输出的表的解读,如图9

图9
如果p值比α要小,那么认为具有显著性差异。图9中的α是以0.05为例进行讲解的。
最终可以通过判断p值判断是否有显著性差异,p<α那么差异是显著的,p<α那么差异是高度显著的,p>α可以认为没有显著性差异。一种方法是直接看p值(F)的信息。另一种方法是比较F真实值和F查表值的大小关系,n是总体 的df,m是列的df。n是143,m是3,可以查表得到F查表值是3.926,因为F查表值<F真实值=13.48,则认为四种广告方式下的销售量有显著性差异。通过图5和图7可以看出,最后一种类型的广告效果是有显著的不同的。
- 在设计广告效果的试验时,虽然地区差异对销售量的影响并不是我们感兴趣的,但希望排除这一因素的影响。数据集 ADS 记录了各个销售点所在的地区 AREA试用双因素方差分析方法分析销售数据,并指出广告方式和地区对销售量是否有显著影响(a=0.01,0.1)? 广告方式(AD)与地区(AREA)之间有无交互效应?
解题:使用matlab的anova2(x,reps)函数,x为要分析的数据,行数必须为reps的倍数。X的不同行是一个因素的不同水平,X的不同列是另外一个因素的不同水平的数据
anova2函数是用来进行双因素一元方差分析的,也就是分析两个因素在同一元上的数据。同样也是通过判断p值来确定不同因素在数据上是否有显著性差异以及不同的因素是否有交互影响。我分析的数据中,行是不同的广告方式,列是不同的地区。代码运行结果如图11,可知,在α=0.01的情况下,地区对销售量没有显著性影响,而广告方式具有,且二者交互效应不显著。在α=0.1的情况下,地区对销售量没有影响,而广告方式具有,且二者交互效应不显著。
代码如图10
![]()
图10

图11
相关文章:

方差分析||判断数据是否符合正态分布
方差分析练习题 练习学习笔记: (1) 标准差和标准偏差、均方差是一个东西。标准误差和标准误是一个东西。这两个东西有区别。 (2)单因素方差分析(MATLAB求解) (3)使用an…...

java linq多字段排序时间比较
public static void main(String[] args) {//100万条数据List<CrmInvestSaleUserCount> waitAssignUserList new ArrayList<>();for (int i 0; i < 1000000; i) {waitAssignUserList.add(new CrmInvestSaleUserCount().setSales_username("test" i…...

【c++】rand()随机函数的应用(二)——舒尔特方格数字的生成
目录 一、舒尔特方格简介 二、如何生成舒尔特方格 (一)线性同余法 1、利用线性同余法生成随机数序列的规律 (1) 当a和c选取合适的数时,可以生成周期为m的随机数序列 (2) 种子seed取值也是有周期的 2、利用线性同余法生成5阶舒尔特方格…...

“深入剖析JVM内部机制:探索Java虚拟机的运行原理“
标题:深入剖析JVM内部机制:探索Java虚拟机的运行原理 摘要:本文将深入探讨Java虚拟机(JVM)的内部机制,包括类加载、内存管理、垃圾回收、即时编译等关键概念和原理,帮助开发者更好地理解JVM的运…...

pandas 新增数据列的几种方式
准备数据 将下面的数据存到csv中 ymd,bWendu,yWendu,tianqi,fengxiang,fengli,aqi,aqiInfo,aqiLevel 2018-01-01,3℃,-6℃,晴~多云,东北风,1-2级,59,良,2 2018-01-02,2℃,-5℃,阴~多云,东北风,1-2级,49,优,1 2018-01-03,2℃,-5℃,多云,北风,1-2级,28,优,1 2018-01-04,0℃,-8℃…...
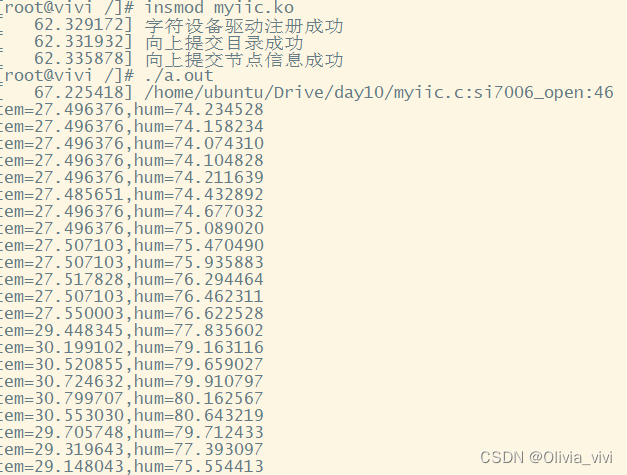
linux_驱动_iic总线获取si7006温湿度
应用层si7006.c #include<stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <unistd.h> #include <stdlib.h> #include <string.h> #include <sys/ioctl.h> #include <arpa/inet.h>…...
虚拟机网络图标不见了
有3台虚拟机之前正常运行的,有一天打开虚拟机发现2台虚拟机的网络连接图标不见了,也ping不通另外两台。 解决:在终端执行以下命令,即可ping通 [roothadoop103 ~]# sudo nmcli network off [roothadoop103 ~]# sudo nmcli network…...
CTF:信息泄露.(CTFHub靶场环境)
CTF:信息泄露.(CTFHub靶场环境) “ 信息泄露 ” 是指网站无意间向用户泄露敏感信息,泄露了有关于其他用户的数据,例如:另一个用户名的财务信息,敏感的商业 或 商业数据 ,还有一些有…...
Redis学习总结
Redis学习总结 文章目录 Redis学习总结Radis基本介绍docker的安装基本数据结构通用命令字符型key的层次结构Hash类型Listset sortedset集合redis的java客户端jedis的使用jedis连接池的配置 SpringDataRedis自定义redistemplate的序列化与反序列化方式stringtemplate的使用 redi…...
云原生全栈体系(二)
Kubernetes实战入门 第一章 Kubernetes基础概念 一、是什么 我们急需一个大规模容器编排系统kubernetes具有以下特性: 服务发现和负载均衡 Kubernetes 可以使用 DNS 名称或自己的 IP 地址公开容器,如果进入容器的流量很大,Kubernetes 可以负…...

C++设计模式之建造者设计模式
C建造者设计模式 什么是建造者设计模式 建造者设计模式是一种创建型设计模式,它是一种将复杂对象的分解为多个独立部分的模式,以便于构建对象的过程可以被抽象出来并独立变化。 该模式有什么优缺点 优点 灵活性:建造者设计模式允许对象的…...

HDFS Erasure coding-纠删码介绍和原理
HDFS Erasure coding-纠删码介绍和原理 三副本策略弊端Erasure Coding(EC)简介Reed- Solomon(RS)码 EC架构 三副本策略弊端 为了提供容错能力,hdfs回根据replication factor(复制因子)在不同的…...
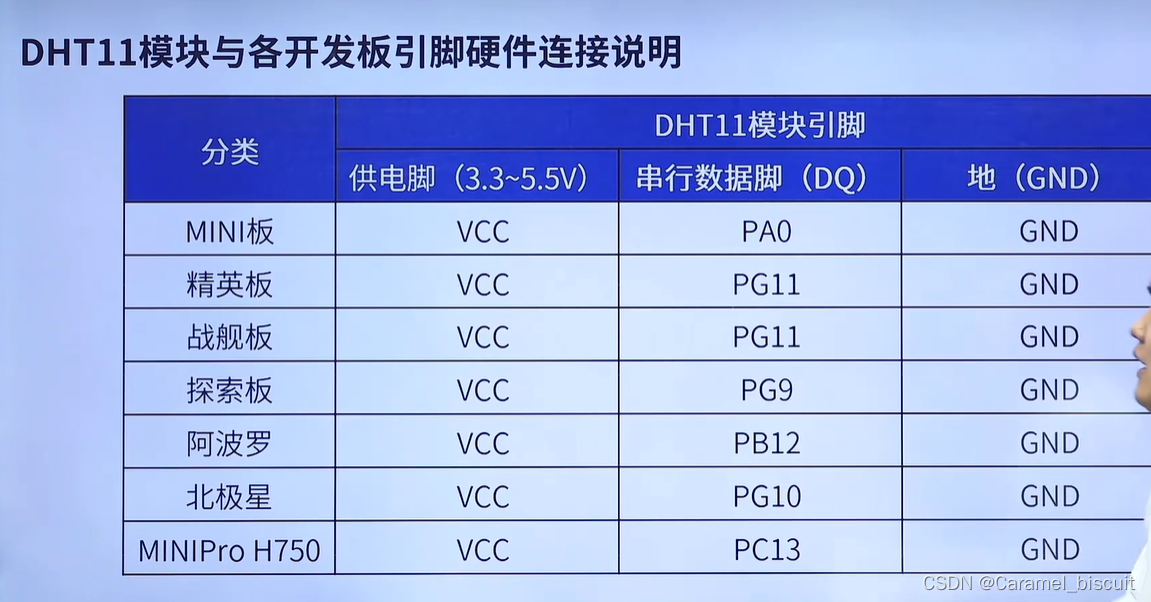
STM32 DHT11
DHT11 DHT11数字温湿度传感器是一款含有已校准数字信号输出的温湿度复合传感器。 使用单总线通信 该传感器包括一个电容式感湿元件和一个NTC测温元件,并于一个高性能8位单片机相连(模数转换)。 DHT11引脚说明 开漏模式下没有输出高电平的能…...

词法分析器
词法分析器 在早期编译1.0时代,我们的目标是完成程序语言到机器语言的翻译,所以重点在编译器前端,于是我们花费大量时间研究词法分析、语法分析、语义分析等内容。如今的本科编译原理课程,基本上也就到这一层面吧。 在编译2.0时…...

【Spring】Spring之启动过程源码解析
概述 我们说的Spring启动,就是构造ApplicationContext对象以及调用refresh()方法的过程。 Spring启动过程主要做了这么几件事情: 构造一个BeanFactory对象解析配置类,得到BeanDefinition,并注册到BeanFactory中 解析ComponentS…...
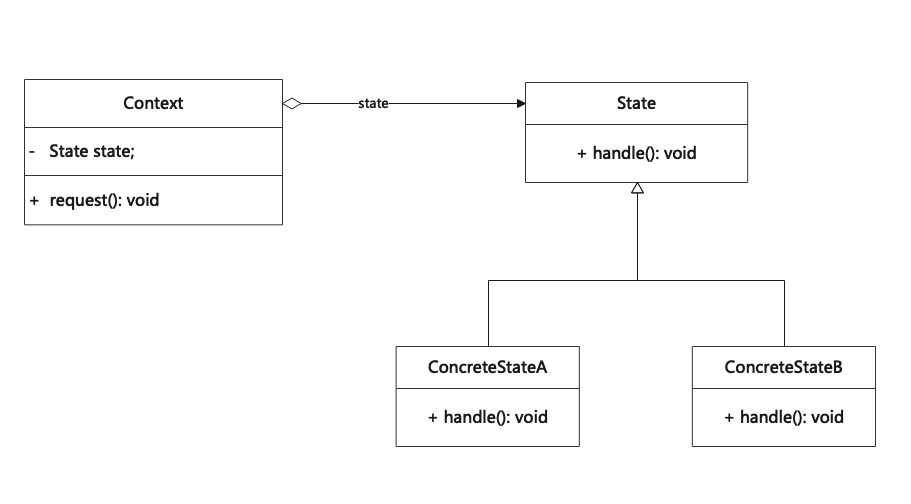
状态模式(State)
状态模式是一种行为设计模式,允许一个对象在其内部状态改变时改变它的行为,使其看起来修改了自身所属的类。其别名为状态对象(Objects for States)。 State is a behavior design pattern that allows an object to change its behavior when its inter…...

【uniapp】样式合集
1、修改uni-data-checkbox多选框的样式为单选框的样式 我原先是用的单选,但是单选并不支持选中后,再次点击取消选中;所以我改成了多选,然后改变多选样式,让他看起来像单选 在所在使用的页面上修改样式即可 <uni-d…...
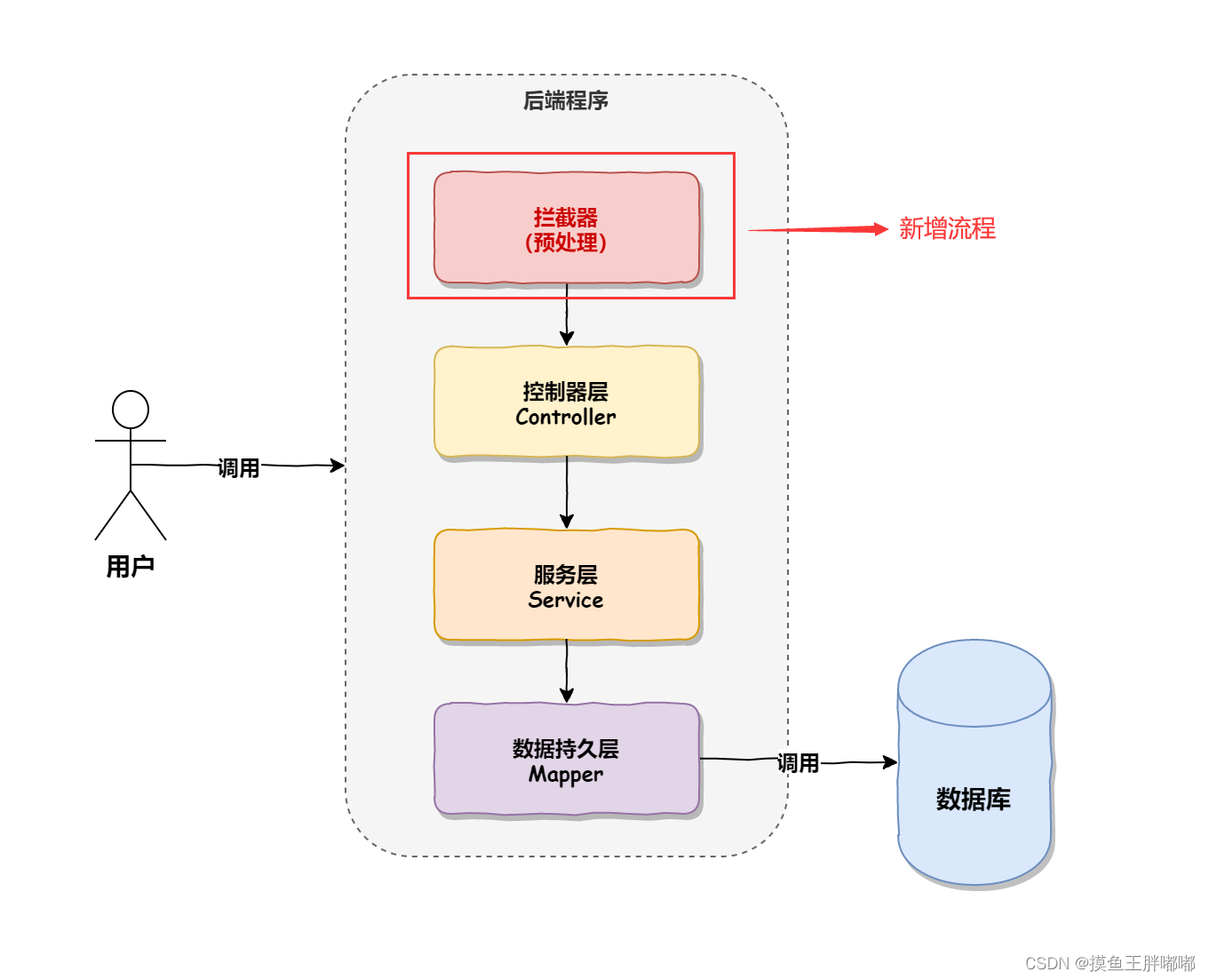
【Spring框架】SpringBoot统一功能处理
目录 用户登录权限校验用户登录拦截器排除所有静态资源练习:登录拦截器拦截器实现原理 统一异常处理统一数据返回格式为什么需要统⼀数据返回格式?统⼀数据返回格式的实现 用户登录权限校验 用户登录拦截器 1.自定义拦截器 package com.example.demo.…...

51单片机学习--按键控制流水灯模式定时器时钟
TMOD负责确定T0和T1的工作模式,TCON控制T0和T1的启动或停止计数,同时包含定时器状态 TF1:定时器1溢出标志 TF0:定时器0溢出标志 0~65535 每隔1微秒计数器1,总时间65535微秒,赋上初值64535,则只…...

Django教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 Django是一个开放源代码的Web应用框架,由Python写成。采用了MTV的框架模式,即模型M,视图V和模版T。它最初是被开发来用于管理劳伦斯出版集团旗下的一些以新闻内容为主的网站的,即是CMS(内容管理系统…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
