数据结构 | 搜索和排序——搜索
目录
一、顺序搜索
二、分析顺序搜索算法
三、二分搜索
四、分析二分搜索算法
五、散列
5.1 散列函数
5.2 处理冲突
5.3 实现映射抽象数据类型
搜索是指从元素集合中找到某个特定元素的算法过程。搜索过程通常返回True或False,分别表示元素是否存在。有时,可以修改搜索过程,使其返回目标元素的位置。
Python提供了运算符in,通过它可以方便地检查元素是否在列表中。
>>> 15 in [3,5,2,4,1]
False
>>> 3 in [3,5,2,4,1]
True一、顺序搜索
存储在列表等集合中的数据项彼此存在线性或顺序关系,每个数据项的位置与其他数据项相关。在Python列表中,数据项的位置就是它的下标。因为下标是有序的,所以能够顺序访问,由此可以进行顺序搜索。
顺序搜索的原理:从列表中的第一个元素开始,沿着默认的顺序逐个查看,直到找到目标元素或者查完列表。如果查完列表后仍没有找到目标元素,则说明目标元素不在列表中。
无序列表的顺序搜索:
def sequentialSearch(alist,item):pos=0found=Falsewhile pos<len(alist) and not found:if alist[pos]==item:found=Trueelse:pos=pos+1return found二、分析顺序搜索算法
| 最好情况 | 最坏情况 | 普通情况 | |
|---|---|---|---|
| 存在目标元素 | 1 | n | n/2 |
| 不存在目标元素 | n | n | n |
有序列表的顺序搜索:
def orderedSequentialSearch(alist,item):pos=0found=Falsestop=Falsewhile pos<len(alist) and not found and not stop:if alist[pos]==item:found=Trueelse:if alist[pos]>item:stop=Trueelse:pos=pos+1return found只有当列表不存在目标元素时,有序排列元素才会提高顺序搜索的效率。
| 最好情况 | 最坏情况 | 普通情况 | |
|---|---|---|---|
| 存在目标元素 | 1 | n | n/2 |
| 不存在目标元素 | 1 | n | n/2 |
三、二分搜索
在顺序搜索时,如果第一个元素不是目标元素,最多还要比较n-1次。但二分搜索不是从第一个元素开始搜索,而是从中间的元素着手。如果这个元素是目标元素,那就立即停止搜索;如果不是,则可以利用列表有序的特性,排除一半的元素。如果目标元素比中间的元素大,就可以直接排除列表左半部分和中间的元素。这是因为,如果列表包含目标元素,它必定位于右半部分。
有序列表的二分搜索:
def binarySearch(alist,item):first=0last=len(alist)-1found=Falsewhile first<=last and not found:midpoint=(first+last)//2if alist[midpoint]==item:found=Trueelse:if item<alist[midpoint]:last=midpoint-1else:first=midpoint+1return found这个算法是分治策略的好例子。分治是指将问题分解成小问题,以某种方式解决小问题,然后整合结果,以解决最初的问题。对列表进行二分搜索时,先查看中间的元素。如果目标元素小于中间的元素,就只需要对列表的左半部分进行二分搜索。同理,如果目标元素更大,则只需对右半部分进行二分搜索。两种情况下,都是针对一个更小的列表递归调用二分搜索函数。
二分搜索的递归版本:
def binarySearch(alist,item):if len(alist)==0:return Falseelse:midpoint=len(alist)//2if alist[midpoint]==item:return Trueelse:if item<alist[midpoint]:return binarySearch(alist[:midpoint],item)else:return binarySearch(alist[midpoint+1:],item)四、分析二分搜索算法
二分搜索算法的时间复杂度是O(logn)。
尽管二分搜索通常优于顺序搜索,但当n较小时,排序引起的额外开销可能并不划算。实际上应该始终考虑,为了提高搜索效率,额外排序是否值得。如果排序一次后能够搜索多次,那么排序的开销不值一提。然而,对于大型列表而言,只排序一次也会有昂贵的计算成本,因此从头进行顺序排序可能是更好的选择。
五、散列
通过散列可以构建一个时间复杂度为O(1)的数据结构。
散列表是元素集合,其中的元素以一种便于查找的方式存储。散列表中的每个位置通常被称为槽,其中可以存储一个元素。槽用一个从0开始的整数标记,例如0号槽、1号槽、2号槽,等等。初始情形下,散列表中没有元素,每个槽都是空的。可以用列表来实现散列表,并将每个元素初始化为Python中的特殊值None。
散列函数将散列表中的元素与其所属位置对应起来。对散列表中的任一元素,散列函数返回一个介于0和m-1之间的整数。首先来看第一个散列函数,它有时被称作“取余函数”,即用一个元素除以表的大小,并将得到的余数作为散列值。取余函数是一个很常见的散列函数,这是因为结果必须在槽编号范围内。
计算出散列值后,就可以将每个元素插入到相应的位置。在11个槽中,有六个被占用。占用率被称为载荷因子,记作,定义如下:
=元素个数/散列表大小。
搜索目标元素时,仅需使用散列函数计算出该元素的槽编号,并查看对应的槽中是否有值。因为计算散列值并找到相应位置所需的时间是固定的,所以搜索操作的时间复杂是O(1)。
如果两个元素的散列值相同,散列函数会将两个元素都放入同一个槽,这种情况叫作冲突,也叫做“碰撞”。显然,冲突给散列函数带来了问题。
5.1 散列函数
给定一个元素集合,能将每个怨怒是映射到不同的槽,这种散列函数称作完美散列函数。
我们的目标是创建这样一个散列函数:冲突数最少,计算方便,元素均匀分布于散列表中。有多种常见的方法来扩展取余函数,下面介绍其中的几种。
折叠法先将元素切成等长的部分(最后一部分的长度可能不同),然后将这些部分相加,得到散列值。假设元素是电话号码436-555-4601,以2位为一组进行切分,得到43、65、55、46和01,将这些数字相加后,得到210.假设散列表有11个槽,接着需要用210除以1,并保留余数1,所以,电话号码436-555-4601被映射到散列表的1号槽。有些折叠法更进一步,在加总前每隔一个数反转一次。就本例而言,反转后的结果是:43+56+55+64+01=219,219%11=10。
另一个构建散列函数的数学技巧是平方取中法:先将元素取平方,然后提取中间几位数。如果元素是44,先计算44*44=1936,然后提取中间两位93,继续进行取余的步骤,得到5(93%11)。
我们也可以为基于字符的元素(比如字符串)创建散列函数。可以将单词"cat"看作序数值序列,如下所示:
>>> ord('c')
99
>>> ord('a')
97
>>> ord('t')
116因此,可以将这些序数值相加,并采用取余法得到散列值。
def hash(astring,tablesize):sum=0for pos in range(len(astring)):sum=sum+ord(astring[pos])return sum%tablesize有趣的是,针对异序词,这个散列函数总是得到相同的散列值。要弥补这一点,可以同字符位置作为权重因子。
def hash(astring,tablesize):sum=0for pos in range(len(astring)):sum=sum+ord(astring[pos])*(pos+1)return sum%tablesize5.2 处理冲突
当两个元素被分到同一个槽中时,必须通过一种系统化方法在散列表中安置第二个元素。这个过程被称为处理冲突。
一种方法是在散列表中找到另一个空槽,用于放置引起冲突的元素。简单的做法是从起初的散列值开始,顺序遍历散列表,知道找到一个空槽。注意,为了遍历散列表,可能需要往回检查第一个槽。这个过程被称为开放定址法,它尝试在散列表中寻找下一个空槽或地址。由于是逐个访问槽,因此这个做法被称作线性探测。
线性探测有个缺点,那就是会使散列表中的元素出现聚集现象。也就是说,如果一个槽发生太多冲突,线性探测会填满附近的槽,而这会影响后续插的元素。要避免元素聚集,一种方法是扩展线性探测,不再依次顺序查找空槽,而是跳过一些槽,这样做能使引起冲突的元素分布得更均匀。采用“加3”探测策略处理冲突后的元素是指发生冲突时,为了找到空槽,该策略每次跳两个槽。
再散列泛指在发生冲突后寻找另一个槽的过程。采用线性探测时,再散列函数是newhashvalue=rehash(oldhanshvalue),并且rehash(pos)=(pos+1)%sizeoftable。“加3”探测策略的再散列函数可以定义为rehash(pos)=(pos+3)%sizeoftable。也就是说,可以将再散列函数定义为rehash(pos)=(pos+skip)%sizeoftable。注意,“跨步(skip)的大小要能够保证表中所有的槽最终都被访问到,否则就会浪费槽资源。要保证这一点,常常建议散列表的大小为素数。
平方探测是线性探测的一个变体,它不采用固定的跨步,而是通过再散列函数递增散列值。如果第一个散列值是h,后续的散列值就是h+1、h+4、h+9、h+16,等等。换句话说,平方探测的跨步是一系列完全平方数。
另一种处理冲突的方法就是让每个槽有一个指向元素集合(或链表)的引用。链接法允许散列表中的同一个位置上存在多个元素。发生冲突时,元素仍然被插入其散列值对应的槽中。不过,随着同一个位置上的元素越来越多,搜索变得越来越困难。
5.3 实现映射抽象数据类型
字典是最有用的Python集合之一。字典是存储键-值对的数据类型。键用来查找关联的值,这个概念常常被称作映射。
映射抽象数据类型定义如下。它是将键和值关联起来的无序集合,其中的键是不重复的,键和值之间是一一对应的关系。映射支持以下操作。
- Map()创建一个空的映射,它返回一个空的映射集合。
- put(key,val)往映射中加入一个新的键值对。如果键已经存在,就用新值替换旧值。
- get(key)返回key对应的值。如果key不存在,则返回None。
- del通过del map[key]这样的语句从映射中删除键-值对。
- len()返回映射中存储的键-值对的数目。
- in通过key in map这样的语句,在键存在时返回True,否则返回False。
class HashTable:def __init__(self):self.size=11self.slots=[None]*self.sizeself.data=[None]*self.sizedef put(self,key,data):hashvalue=self.hashfunction(key,len(self.slots))if self.slots[hashvalue]==None:self.slots[hashvalue]=keyself.data[hashvalue]=dataelse:if self.slots[hashvalue]==key:self.data[hashvalue]=data #替换else:nextslot=self.rehash(hashvalue,len(self.slots))while self.slots[nextslot]!=None and self.slots[nextslot]!=key:nextslot=self.rehash(nextslot,len(self.slots))if self.slots[nextslot]==None:self.slots[nextslot]=keyself.data[nextslot]=dataelse:self.data[nextslot]=data #替换def hashfunction(self,key,size):return key%sizedef rehash(self,oldhash,size):return (oldhash+1)%sizedef get(self,key):startslot=self.hashfunction(key,len(self.slots))data=Nonestop=Falsefound=Falseposition=startslotwhile self.slots[position]!=None and not found and not stop:if self.slots[position]==key:found=Truedata=self.data[position]else:position=self.rehash(position,len(self.slots))if position==startslot:stop=Truereturn datadef __getitem__(self, key):return self.get(key)def __setitem__(self, key, data):self.put(key,data)if __name__=="__main__":H=HashTable()H[54]="cat"H[26]="dog"H[93]="lion"H[17]="tiger"H[77]="bird"H[31]="cow"H[44]="goat"H[55]="pig"H[20]="chicken"print(H.slots)print(H.data)print(H[20])print(H[17])H[20]="duck"print(H[20])print(H.data)print(H[99])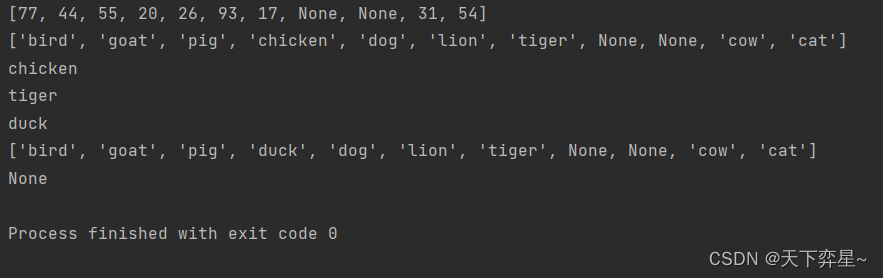
HashTable类的最后两个方法提供了额外的字典功能。我们重载__getitem__和__settiem__ ,以通过[ ]进行访问。这意味着创建HashTable类之后,就可以使用熟悉的索引运算符了。
相关文章:

数据结构 | 搜索和排序——搜索
目录 一、顺序搜索 二、分析顺序搜索算法 三、二分搜索 四、分析二分搜索算法 五、散列 5.1 散列函数 5.2 处理冲突 5.3 实现映射抽象数据类型 搜索是指从元素集合中找到某个特定元素的算法过程。搜索过程通常返回True或False,分别表示元素是否存在。有时&a…...

【python】对象
对象 初识对象成员方法类和对象构造方法其它内置方法封装继承类型注释多态综合案例二级目录三级目录 初识对象 设计表格-生产表格-填写表格 对应于程序中:设计类-创建对象-对象属性赋值 class Student:nameNonegenderNone # 基于类创建对象 stu_1Student() stu_2S…...

k8s概念-污点与容忍
k8s 集群中可能管理着非常庞大的服务器,这些服务器可能是各种各样不同类型的,比如机房、地理位置、配置等,有些是计算型节点,有些是存储型节点,此时我们希望能更好的将 pod 调度到与之需求更匹配的节点上。 此时就需要…...

“从零开始学习Spring Boot:构建高效、可扩展的Java应用程序“
标题:从零开始学习Spring Boot:构建高效、可扩展的Java应用程序 简介: Spring Boot是一种用于简化Java应用程序开发的开源框架,它提供了一种快速、高效的方式来构建可扩展的应用程序。本文将介绍如何从零开始学习Spring Boot&…...
通向架构师的道路之tomcat集群
一、为何要集群 单台App Server再强劲,也有其瓶劲,先来看一下下面这个真实的场景。 当时这个工程是这样的,tomcat这一段被称为web zone,里面用springws,还装了一个jboss的规则引擎Guvnor5.x,全部是ws没有se…...

结构体,枚举,联合大小的计算规则
目录 1.结构体大小的计算 补充(位段) 2.枚举的大小(4个字节) 3.联合大小的计算 1.结构体大小的计算 (1)结构体内存对齐的规则 1. 第一个成员在与结构体变量偏移量为 0 的地址处。 2. 其他成员变量要对…...
Vue2 第十七节 Vue中的Ajax
1.Vue脚手架配置代理 2.vue-resource 一.Vue脚手架配置代理 1.1 使用Ajax库 -- axios ① 安装 : npm i axios ② 引入: import axios from axios ③ 使用示例 1.2 解决开发环境Ajax跨域问题 跨域:违背了同源策略,同源策略规定协议名࿰…...

ES6 - 字符串新增的一些常用方法
文章目录 0,新增的一些方法1,includes()、startsWith()、endsWith()2,repeat()3,padStart()、padEnd()4,trimStart()、trimEnd()5,replaceAll()6,at() 0,新增的一些方法 介绍一些ES6…...

最新SQLMap安装与入门技术
点击星标,即时接收最新推文 本文选自《web安全攻防渗透测试实战指南(第2版)》 五折购买链接:u.jd.com/3ibjeF6 SQLMap详解 SQLMap是一个自动化的SQL注入工具,其主要功能是扫描、发现并利用给定URL的SQL注入漏洞。SQLMa…...
Java 使用 Google Guava 实现接口限流
一、引入依赖 <dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>30.0-jre</version> </dependency>二、自定义注解及限流拦截器 自定义注解:Limiter package com.haita…...
帮助中心的价值是什么?怎样才能在线搭建官网网站帮助中心?
帮助中心(Help Center)是一个提供公司或组织产品或服务相关信息的在线平台。它的价值在于为用户提供便捷的自助服务和解决问题的渠道,同时也能减轻客服人员的负担。 如何在线搭建官网网站帮助中心的步骤 确定需求:在搭建帮助中心…...
Kubernetes——理论基础
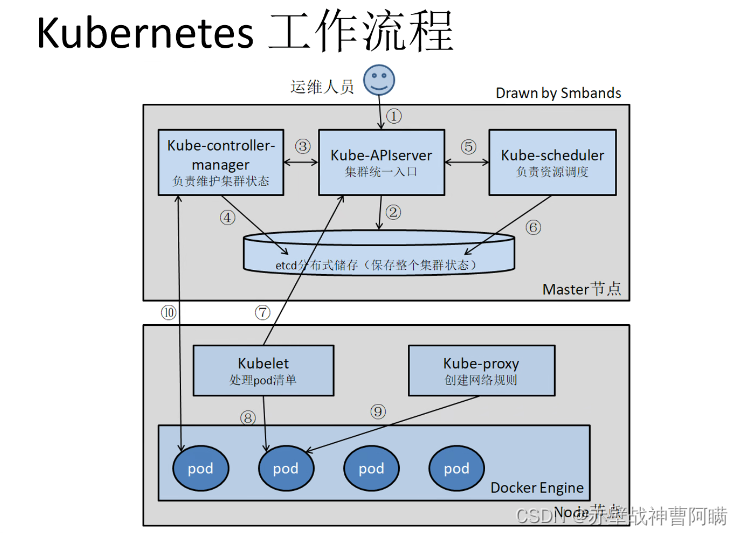
Kubernetes——理论基础 一、Kubernetes 概述1.K8S 是什么?2.为什么要用 K8S?3.Kubernetes 主要功能 二、Kubernetes 集群架构与组件三、Master 组件1.Kube-apiserver2.Kube-controller-manager3.Kube-scheduler4.配置存储中心——etcd 四、Node 组件1.Kubelet2.Ku…...

【VUE3】
Vue 3 是当下最流行的前端框架之一,其主要特点是性能更好、体积更小、更易于维护。下面是 Vue 3 的一些重要知识点和代码示例: 创建 Vue 实例 import { createApp } from vueconst app createApp({data() {return {message: Hello, Vue 3!}} })app.mo…...

《金融数据保护治理白皮书》发布(137页)
温馨提示:文末附完整PDF下载链接 导读 目前业界已出台数据保护方面的治理模型,但围绕金融数据保护治理的实践指导等尚不成熟,本课题围绕数据保护治理的金融实践、发展现状,探索和标准化相关能力要求,归纳总结相关建…...
上海亚商投顾:沪指震荡微涨 金融、地产午后大幅走强
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 市场情绪 三大指数早盘震荡,午后集体拉升反弹,创业板指涨超1%。券商等大金融板块午后再度走强&#…...

Linux文件管理知识:查找文件
前几篇文章一一介绍了LINUX进程管理控制命令及网络层面的知识体系,综所周知,一个linux系统是由很多文件组成的,那么既然有那么多文件,那我们该如何管理这些文件呢? Linux中的所有数据都是以文件形式存在的,…...

【TypeScript】安装的坑!
TypeScript安装 安装TypeScript安装时候可能报错这样开头的数据(无法枚举容器中的对象)——原因:没权限先解决没权限的问题如果发现无法修改-高级-修改继续安装想使用tsc-发现,tsc不能用解决方法:配置环境变量最后的最…...

spring boot 2.x 使用 jpa 映射 json mysql列数据映射乱码
通过下面的依赖,可以将 mysql 的 json 列字段(mysql 5.7及以上的版本支持),映射成 Java Bean <dependency><groupId>com.vladmihalcea</groupId><artifactId>hibernate-types-52</artifactId><v…...

创建Helm脚本
一、创建脚本 Helm 是 Kubernetes 的包管理工具,它可以帮助您简化和自动化 Kubernetes 应用程序的部署和管理。使用 Helm,您可以创建和管理称为 Helm Chart 的应用程序打包,这些 Chart 包含了 Kubernetes 资源和配置信息,可以在不…...
2.05 购物车后台刷新并显示
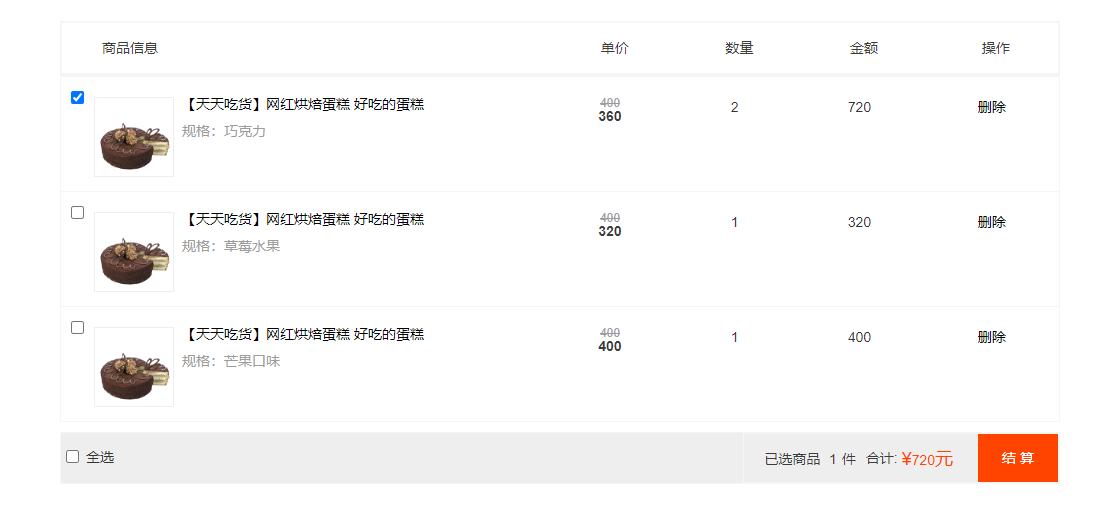
一.用户登录添加商品使用cookie存入购物车,并把购物车商品传入到后台 步骤1:创建购物车BO对象 public class ShopcartBO {private String itemId;private String itemImgUrl;private String itemName;private String specId;private String specName;p…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
