【LinearAlgebra】Chapter 12 - Linear Algebra in Probability Statistics

文章目录
- Chapter 12 - Linear Algebra in Probability & Statistics
- Variance (around athe mean) 方差(接近均值)
- Continuous Probability Distributions 连续概率分布
- Mean and Variance of p ( x ) p(x) p(x) p ( x ) p(x) p(x) 的均值和方差
- Normal Distribution: Bell-shaped Curve
- N Coin Flips and N → ∞ N \rightarrow \infty N→∞
- Monte Carlo Estimation Methods
- Review: Three Formulas for the Mean and the Variance
- 12.2 Covariance Matrices and Joint Probabilities
- 12.3 Multivariate Gaussian and Weighted Least Squares
- Ref
Chapter 12 - Linear Algebra in Probability & Statistics
我们从本章的三个基本词汇开始:均值(mean)、方差(variance)和概率(probability)。在写公式之前,让我先粗略地解释一下它们的含义:
平均值指平均值或期望值
方差 σ 2 \sigma^2 σ2 衡量与平均值 m m m 的平均平方距离
n n n 种不同结果的概率都是正数 p 1 , ⋯ , p n p_1, \cdots, p_n p1,⋯,pn 相加为 1 1 1。
当然,平均数很容易理解。我们从这里开始。但是现在我们有两种不同的情况,你们必须弄清楚。一方面,我们可以从完成的试验中得到结果(样本值)。另一方面,我们可能从未来的试验中得到预期的结果(期望值)。让我举几个例子:
样本值 随机抽取 5 5 5 名新生,年龄分别为 18 、 17 、 18 、 19 、 17 18、17、18、19、17 18、17、18、19、17
样本均值 1 5 ( 18 + 17 + 18 + 19 + 17 ) = 17.8 \frac{1}{5}(18 + 17 + 18 + 19 + 17) = 17.8 51(18+17+18+19+17)=17.8
概率 大一新生的年龄分别是 17 17 17 岁( 20 % 20\% 20%)、 18 18 18 岁( 50 % 50\% 50%)、 19 19 19 岁( 30 % 30\% 30%)。
随机选择一个大一新生的预期年龄 E [ x ] = ( 0.2 ) 17 + ( 0.5 ) 18 + ( 0.3 ) 19 = 18.1 \text{E}[x] = (0.2) 17 + (0.5) 18 + (0.3) 19 = 18.1 E[x]=(0.2)17+(0.5)18+(0.3)19=18.1
17.8 17.8 17.8 和 18.1 18.1 18.1 都是正确的平均值。样本均值 N N N 个采样点 x 1 , ⋯ , x N x_1, \cdots, x_N x1,⋯,xN 从一个完成的试验开始。它们的平均值是 N N N 个观测样本的平均值:
样本均值 m = μ = 1 N ( x 1 + x 2 + ⋯ + x N ) (1) m = \mu = \frac{1}{N} (x_1 + x_2 + \cdots + x_N) \tag{1} m=μ=N1(x1+x2+⋯+xN)(1)
x x x 的期望值开始于年龄 x 1 , ⋯ , x n x_1, \cdots, x_n x1,⋯,xn 的概率 p 1 , ⋯ , x n p_1, \cdots, x_n p1,⋯,xn:
期望值 m = E [ x ] = p 1 x 1 + p 2 x 2 + ⋯ + p n x n (2) m = \text{E}[x] = p_1 x_1 + p_2 x_2 + \cdots + p_n x_n \tag{2} m=E[x]=p1x1+p2x2+⋯+pnxn(2)
这就是 p ⋅ x p \cdot x p⋅x。注意 m = E [ x ] m = \text{E}[x] m=E[x] 告诉了我们期望什么, m = μ m= μ m=μ 告诉我们得到什么。
通过取很多样本(比如说一个很大的 N N N),样本结果将接近概率。“大数定律(Law of Large Numbers)”认为,随着样本量 N N N 的增加,样本均值以 1 1 1 的概率收敛于其期望值 E [ x ] \text{E}[x] E[x]。一枚均匀硬币出现背面的概率为 p 0 = 1 2 p_0=\frac{1}{2} p0=21,出现正面的概率为 p 1 = 1 2 p_1=\frac{1}{2} p1=21。然后 E [ x ] = ( 1 2 ) 0 + ( 1 2 ) 1 \text{E} [x] = (\frac{1}{2}) 0 + (\frac{1}{2}) 1 E[x]=(21)0+(21)1。 N N N 次抛硬币中正面出现的比例是样本均值,接近期望 E [ x ] = 1 2 \text{E}[x] =\frac{1}{2} E[x]=21。
这并不意味着如果我们看到的反面多于正面,那么下一个样本很可能是正面。几率仍然是 50 % 50\% 50%。前 100 100 100 次或 1000 1000 1000 次投掷确实会影响样本均值。但是 1000 1000 1000 次抛硬币不会影响它的极限——因为你要除以 N → ∞ N \rightarrow \infty N→∞。
Variance (around athe mean) 方差(接近均值)
方差 σ 2 \sigma^2 σ2 表示到期望均值 E [ x ] \text{E}[x] E[x] 的期望距离(平方)。样本方差 S 2 S^2 S2 表示离样本均值的实际距离(平方)。平方根是标准差 σ σ σ 或 S S S。
样本方差 S 2 = 1 N − 1 [ ( x 1 − m ) 2 + ⋯ + ( x N − m ) 2 ] (3) S^2 = \frac{1}{N-1} [(x_1-m)^2 + \cdots + (x_N-m)^2] \tag{3} S2=N−11[(x1−m)2+⋯+(xN−m)2](3)
样本年龄 x = 18 , 17 , 18 , 19 , 17 x=18,17,18,19,17 x=18,17,18,19,17 有均值 m = 17.8 m = 17.8 m=17.8。样本有方差 0.7 0.7 0.7:
S 2 = 1 5 − 1 [ ( . 2 ) 2 + ( − . 8 ) 2 + ( . 2 ) 2 + ( 1.2 ) 2 + ( − . 8 ) 2 ] = 1 4 ( 2.8 ) = 0.7 S^2 = \frac{1}{5-1} [(.2)^2 + (-.8)^2 + (.2)^2 + (1.2)^2 + (-.8)^2] = \frac{1}{4}(2.8) = 0.7 S2=5−11[(.2)2+(−.8)2+(.2)2+(1.2)2+(−.8)2]=41(2.8)=0.7
当我们计算平方时,负号消失了。请注意!统计学家除以 N − 1 = 4 N - 1 = 4 N−1=4(而不是 N = 5 N = 5 N=5),因此 S 2 S^2 S2 是 σ 2 \sigma^2 σ2 的无偏估计。样本均值中已经包含了一个自由度。
一个重要的恒等式来自于将每个 ( x − m ) 2 (x-m)^2 (x−m)2 分成 x 2 − 2 m x + m 2 x^2- 2mx + m^2 x2−2mx+m2:
sum of ( x i − m ) 2 = ( sum of x i 2 ) + 2 m ( sum of x i ) + ( sum of m 2 ) = ( sum of x i 2 ) + 2 m ( N m ) + N m 2 sum of ( x i − m ) 2 = ( sum of x i 2 ) − N m 2 (4) \begin{aligned} \text{sum of } (x_i - m)^2 &= (\text{sum of } x_i^2) + 2m(\text{sum of } x_i) + (\text{sum of } m^2) \\ &= (\text{sum of } x_i^2) + 2m(Nm) + N m^2 \\ \text{sum of } (x_i - m)^2 &= (\text{sum of } x_i^2) - N m^2 \end{aligned} \tag{4} sum of (xi−m)2sum of (xi−m)2=(sum of xi2)+2m(sum of xi)+(sum of m2)=(sum of xi2)+2m(Nm)+Nm2=(sum of xi2)−Nm2(4)
这是一个通过添加 x 1 2 + ⋯ + x N 2 x_1^2 + \cdots + x_N^2 x12+⋯+xN2 来找寻 ( x 1 − m ) 2 + ⋯ + ( x N − m ) (x_1-m)^2+\cdots+(x_N-m) (x1−m)2+⋯+(xN−m) 的等价方式。
现在从概率 p i p_i pi (绝不会是负值)开始,而不再是样本。我们找到期望值而不是样本值。方差 σ 2 \sigma^2 σ2 是统计学中的关键数字。
方差 σ 2 = E [ ( x − m ) 2 ] = p 1 ( x 1 − m ) 2 + ⋯ + p n ( x n − m ) 2 (5) \sigma^2 = \text{E} [(x-m)^2] = p_1 (x_1-m)^2 + \cdots + p_n (x_n-m)^2 \tag{5} σ2=E[(x−m)2]=p1(x1−m)2+⋯+pn(xn−m)2(5)
我们对期望值 m = E [ x ] m = \text{E}[x] m=E[x] 的距离进行平方。我们没有样本,只期望。我们知道概率,但我们不知道实验结果。
Continuous Probability Distributions 连续概率分布
到目前为止,我们有 n n n 种可能的结果 x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn。如果样本年龄为 17 、 18 、 19 17、18、19 17、18、19 岁时,只有 n = 3 n = 3 n=3。如果我们用天而不是年来衡量年龄,那么就会有一千种可能的年龄(太多了)。最好允许 17 17 17 到 20 20 20 岁之间的每个数字——一个可能年龄的连续体。那么年龄 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3 岁的概率 p 1 , p 2 , p 3 p_1, p_2, p_3 p1,p2,p3 必须移动到概率分布(probability distribution) p ( x ) p(x) p(x) 在 17 ≤ x ≤ 20 17 \le x \le 20 17≤x≤20 的连续范围内。
解释概率分布的最好方法是举两个例子。它们是均匀分布(uniform distribution)和正态分布(normal distribution)。均匀分布很容易。正态分布非常重要。
均匀分布
假设年龄均匀分布在 17.0 17.0 17.0 到 20.0 20.0 20.0 之间。这些数字之间的所有年龄都是“同等可能的”。当然,任何一个确切的年龄都没有机会。你得到 x = 17.1 x = 17.1 x=17.1 或 x = 17 + 2 x=17+ \sqrt{2} x=17+2 的概率为零。你可以真实地提供(假设我们的均匀分布)一个新生年龄小于 x x x 的概率 F ( x ) F(x) F(x):
年龄小于 x = 17 x=17 x=17 的概率为 F ( 17 ) = 0 F(17)=0 F(17)=0, x ≤ 17 x\le 17 x≤17 永远不会发生
年龄小于 x = 20 x=20 x=20 的概率为 F ( 20 ) = 1 F(20)=1 F(20)=1, x ≤ 20 x\le 20 x≤20 会发生
年龄小于 x x x 的概率为 F ( x ) = 1 3 ( x − 17 ) F(x)=\frac{1}{3}(x-17) F(x)=31(x−17), F F F 从 0 0 0 到 1 1 1
公式 F ( x ) = 1 3 ( x − 17 ) F(x) = \frac{1}{3}(x-17) F(x)=31(x−17) 给出在 x = 17 x= 17 x=17 处 F = 0 F = 0 F=0;那么 x < 17 x < 17 x<17 就不会发生。它给出在 x = 20 x= 20 x=20 处 F ( x ) = 1 F(x)=1 F(x)=1;那么 x ≤ 20 x \le 20 x≤20 是肯定的。在 17 17 17 和 20 20 20 之间,这个均匀模型的累积分布(cumulative distribution) F ( x ) F(x) F(x) 的图呈线性增长。
画出 F ( x ) F(x) F(x) 的图和它的导数 p ( x ) = p(x) = p(x)= 概率密度函数(probability density function)。

你可以说 p ( x ) d x p(x) \text{d}x p(x)dx 是样本落在 x x x 和 x + d x x+\text{d}x x+dx 之间的概率。这是极其真实的(infinitesimally true): p ( x ) d x p(x) \text{d}x p(x)dx 等于 F ( x + d x ) − F ( x ) F(x+\text{d}x) - F(x) F(x+dx)−F(x)。以下是完整描述:
F = integral of p Probability of a ≤ x ≤ b = ∫ a b p ( x ) d x = F ( b ) − F ( a ) (6) F = \text{integral of } p \quad \text{ Probability of} a \le x \le b = \int_{a}^{b} p(x) \text{d}x = F(b) - F(a) \tag{6} F=integral of p Probability ofa≤x≤b=∫abp(x)dx=F(b)−F(a)(6)
F ( b ) F(b) F(b) 是 x ≤ b x \le b x≤b 的概率。我减去 F ( a ) F(a) F(a) 使 x ≥ a x \ge a x≥a 保持不变。这样有 a ≤ x ≤ b a \le x \le b a≤x≤b。
Mean and Variance of p ( x ) p(x) p(x) p ( x ) p(x) p(x) 的均值和方差
一个概率分布的均值 m m m 和方差 σ 2 \sigma^2 σ2 是多少?之前我们添加了 p i x i p_i x_i pixi 来获得均值(期望均值)。对于一个连续分布我们对 x p ( x ) x p(x) xp(x) 积分:
均值 m = E [ x ] = ∫ x p ( x ) d x = ∫ x = 17 20 ( x ) ( 1 3 ) d x = 18.5 m = \text{E}[x] = \int x p(x) \text{d} x = \int_{x=17}^{20} (x) (\frac{1}{3}) \text{d}x = 18.5 m=E[x]=∫xp(x)dx=∫x=1720(x)(31)dx=18.5
对于均匀分布,均值 m m m 介于 17 17 17 和 20 20 20 之间。那么随机值 x x x 低于中点 m = 18.5 m = 18.5 m=18.5 的概率为 F ( m ) = 1 2 F(m) = \frac{1}{2} F(m)=21。
Normal Distribution: Bell-shaped Curve
N Coin Flips and N → ∞ N \rightarrow \infty N→∞
Monte Carlo Estimation Methods
Review: Three Formulas for the Mean and the Variance
12.2 Covariance Matrices and Joint Probabilities
12.3 Multivariate Gaussian and Weighted Least Squares
\begin{aligned} \end{aligned}
Ref
- Introduction to Linear Algebra - GILBERT STRANG
- 为什么分母从n变成n-1之后,就从【有偏估计】变成了【无偏估计】?
相关文章:

【LinearAlgebra】Chapter 12 - Linear Algebra in Probability Statistics
文章目录 Chapter 12 - Linear Algebra in Probability & StatisticsVariance (around athe mean) 方差(接近均值)Continuous Probability Distributions 连续概率分布Mean and Variance of p ( x ) p(x) p(x) p ( x ) p(x) p(x) 的均值和方差Norm…...

webshell详解
Webshell详解 一、 Webshell 介绍二 、 基础常见webshell案例 一、 Webshell 介绍 概念 webshell就是以asp、php、jsp或者cgi等网页文件形式存在的一种命令执行环境,也可以将其称做为一种网页后门。黑客在入侵了一个网站后,通常会将asp或php后门文件与…...
数据结构 | 搜索和排序——搜索
目录 一、顺序搜索 二、分析顺序搜索算法 三、二分搜索 四、分析二分搜索算法 五、散列 5.1 散列函数 5.2 处理冲突 5.3 实现映射抽象数据类型 搜索是指从元素集合中找到某个特定元素的算法过程。搜索过程通常返回True或False,分别表示元素是否存在。有时&a…...

【python】对象
对象 初识对象成员方法类和对象构造方法其它内置方法封装继承类型注释多态综合案例二级目录三级目录 初识对象 设计表格-生产表格-填写表格 对应于程序中:设计类-创建对象-对象属性赋值 class Student:nameNonegenderNone # 基于类创建对象 stu_1Student() stu_2S…...

k8s概念-污点与容忍
k8s 集群中可能管理着非常庞大的服务器,这些服务器可能是各种各样不同类型的,比如机房、地理位置、配置等,有些是计算型节点,有些是存储型节点,此时我们希望能更好的将 pod 调度到与之需求更匹配的节点上。 此时就需要…...

“从零开始学习Spring Boot:构建高效、可扩展的Java应用程序“
标题:从零开始学习Spring Boot:构建高效、可扩展的Java应用程序 简介: Spring Boot是一种用于简化Java应用程序开发的开源框架,它提供了一种快速、高效的方式来构建可扩展的应用程序。本文将介绍如何从零开始学习Spring Boot&…...
通向架构师的道路之tomcat集群
一、为何要集群 单台App Server再强劲,也有其瓶劲,先来看一下下面这个真实的场景。 当时这个工程是这样的,tomcat这一段被称为web zone,里面用springws,还装了一个jboss的规则引擎Guvnor5.x,全部是ws没有se…...

结构体,枚举,联合大小的计算规则
目录 1.结构体大小的计算 补充(位段) 2.枚举的大小(4个字节) 3.联合大小的计算 1.结构体大小的计算 (1)结构体内存对齐的规则 1. 第一个成员在与结构体变量偏移量为 0 的地址处。 2. 其他成员变量要对…...
Vue2 第十七节 Vue中的Ajax
1.Vue脚手架配置代理 2.vue-resource 一.Vue脚手架配置代理 1.1 使用Ajax库 -- axios ① 安装 : npm i axios ② 引入: import axios from axios ③ 使用示例 1.2 解决开发环境Ajax跨域问题 跨域:违背了同源策略,同源策略规定协议名࿰…...

ES6 - 字符串新增的一些常用方法
文章目录 0,新增的一些方法1,includes()、startsWith()、endsWith()2,repeat()3,padStart()、padEnd()4,trimStart()、trimEnd()5,replaceAll()6,at() 0,新增的一些方法 介绍一些ES6…...

最新SQLMap安装与入门技术
点击星标,即时接收最新推文 本文选自《web安全攻防渗透测试实战指南(第2版)》 五折购买链接:u.jd.com/3ibjeF6 SQLMap详解 SQLMap是一个自动化的SQL注入工具,其主要功能是扫描、发现并利用给定URL的SQL注入漏洞。SQLMa…...
Java 使用 Google Guava 实现接口限流
一、引入依赖 <dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>30.0-jre</version> </dependency>二、自定义注解及限流拦截器 自定义注解:Limiter package com.haita…...
帮助中心的价值是什么?怎样才能在线搭建官网网站帮助中心?
帮助中心(Help Center)是一个提供公司或组织产品或服务相关信息的在线平台。它的价值在于为用户提供便捷的自助服务和解决问题的渠道,同时也能减轻客服人员的负担。 如何在线搭建官网网站帮助中心的步骤 确定需求:在搭建帮助中心…...
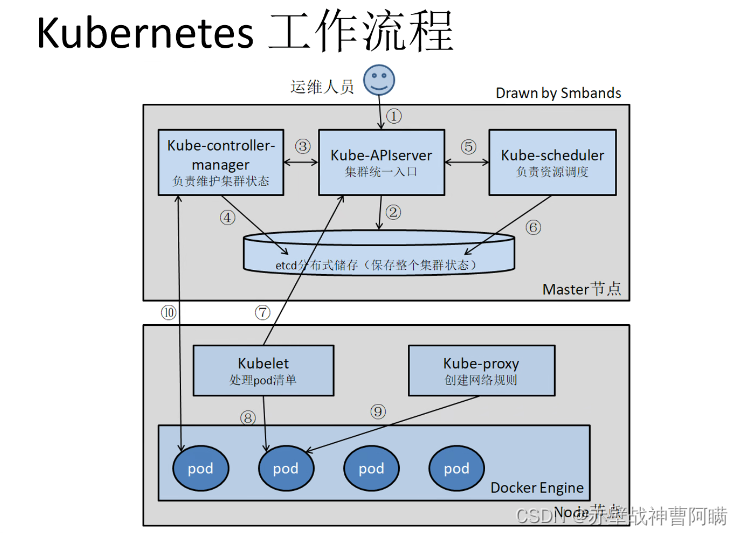
Kubernetes——理论基础
Kubernetes——理论基础 一、Kubernetes 概述1.K8S 是什么?2.为什么要用 K8S?3.Kubernetes 主要功能 二、Kubernetes 集群架构与组件三、Master 组件1.Kube-apiserver2.Kube-controller-manager3.Kube-scheduler4.配置存储中心——etcd 四、Node 组件1.Kubelet2.Ku…...

【VUE3】
Vue 3 是当下最流行的前端框架之一,其主要特点是性能更好、体积更小、更易于维护。下面是 Vue 3 的一些重要知识点和代码示例: 创建 Vue 实例 import { createApp } from vueconst app createApp({data() {return {message: Hello, Vue 3!}} })app.mo…...

《金融数据保护治理白皮书》发布(137页)
温馨提示:文末附完整PDF下载链接 导读 目前业界已出台数据保护方面的治理模型,但围绕金融数据保护治理的实践指导等尚不成熟,本课题围绕数据保护治理的金融实践、发展现状,探索和标准化相关能力要求,归纳总结相关建…...
上海亚商投顾:沪指震荡微涨 金融、地产午后大幅走强
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 市场情绪 三大指数早盘震荡,午后集体拉升反弹,创业板指涨超1%。券商等大金融板块午后再度走强&#…...

Linux文件管理知识:查找文件
前几篇文章一一介绍了LINUX进程管理控制命令及网络层面的知识体系,综所周知,一个linux系统是由很多文件组成的,那么既然有那么多文件,那我们该如何管理这些文件呢? Linux中的所有数据都是以文件形式存在的,…...

【TypeScript】安装的坑!
TypeScript安装 安装TypeScript安装时候可能报错这样开头的数据(无法枚举容器中的对象)——原因:没权限先解决没权限的问题如果发现无法修改-高级-修改继续安装想使用tsc-发现,tsc不能用解决方法:配置环境变量最后的最…...

spring boot 2.x 使用 jpa 映射 json mysql列数据映射乱码
通过下面的依赖,可以将 mysql 的 json 列字段(mysql 5.7及以上的版本支持),映射成 Java Bean <dependency><groupId>com.vladmihalcea</groupId><artifactId>hibernate-types-52</artifactId><v…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
