[PyTorch][chapter 46][LSTM -1]
前言:
长短期记忆网络(LSTM,Long Short-Term Memory)是一种时间循环神经网络,是为了解决一般的RNN(循环神经网络)存在的长期依赖问题而专门设计出来的。
目录:
- 背景简介
- LSTM Cell
- LSTM 反向传播算法
- 为什么能解决梯度消失
- LSTM 模型的搭建
一 背景简介:
1.1 RNN
RNN 忽略 模型可以简化成如下
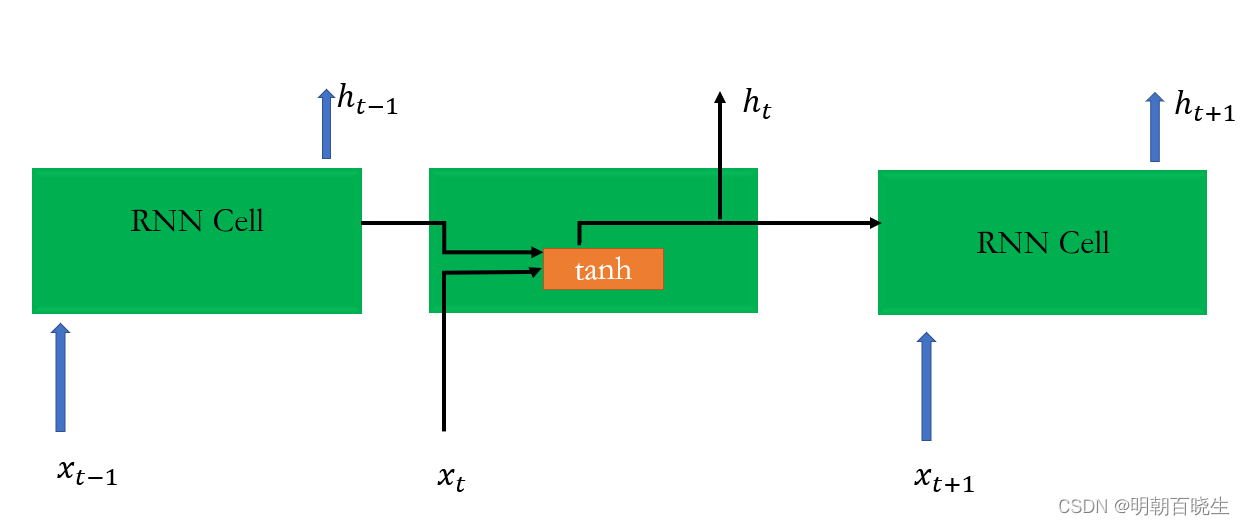
图中Rnn Cell 可以很清晰看出在隐藏状态。
得到 后:
一方面用于当前层的模型损失计算,另一方面用于计算下一层的
由于RNN梯度消失的问题,后来通过LSTM 解决
1.2 LSTM 结构

二 LSTM Cell
LSTMCell(RNNCell) 结构

前向传播算法 Forward
2.1 更新: forget gate 忘记门
将值朝0 减少, 激活函数一般用sigmoid
输出值[0,1]
2.2 更新: Input gate 输入门
决定是不是忽略输入值
2.3 更新: 候选记忆单元
2.4 更新: 记忆单元
2.5 更新: 输出门
决定是否使用隐藏值
2.6. 隐藏状态
2.7 模型输出
LSTM 门设计的解释一:
输入门 ,遗忘门,输出门 不同取值组合的时候,记忆单元的输出情况
三 LSTM 反向传播推导
3.1 定义两个
3.2 定义损失函数
损失函数分为两部分:
时刻t的损失函数
时刻t后的损失函数
3.3 最后一个时刻的

这里面要注意这里的
证明一下第二项,主要应用到微分的两个性质,以及微分和迹的关系:
... 公式1: 微分和迹的关系
因为
带入上面公式1:
所以
3.4 链式求导过程
求导结果:

这里详解一下推导过程:
这是一个符合函数求导:先把h 写成向量形成
------------------------------------------------------------
第一项:
设
则
其中:(利用矩阵求导的定义法 分子布局原理)
是一个对角矩阵
几个连乘起来就是第一项
第二项
参考:
其中:
其它也是相似,就有了上面的求导结果

四 为什么能解决梯度消失
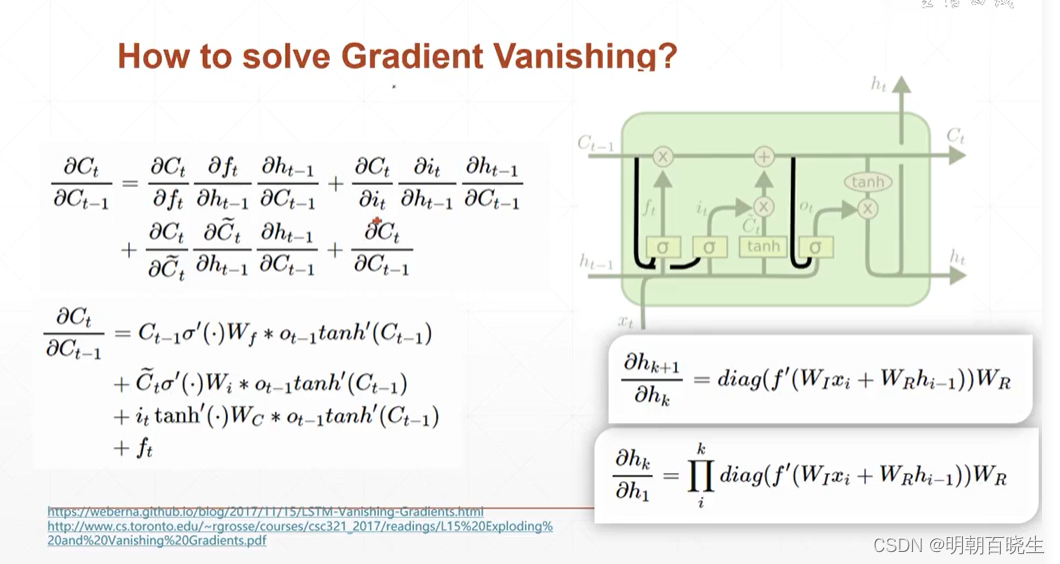
4.1 RNN 梯度消失的原理
,复旦大学邱锡鹏书里面 有更加详细的解释,通过极大假设:
在梯度计算中存在梯度的k 次方连乘 ,导致 梯度消失原理。
4.2 LSTM 解决梯度消失 解释1:
通过上面公式发现梯度计算中是加法运算,不存在连乘计算,
极大概率降低了梯度消失的现象。
4.3 LSTM 解决梯度 消失解释2:
记忆单元c 作用相当于ResNet的残差部分.
比如 时候,
,不会存在梯度消失。
五 模型的搭建

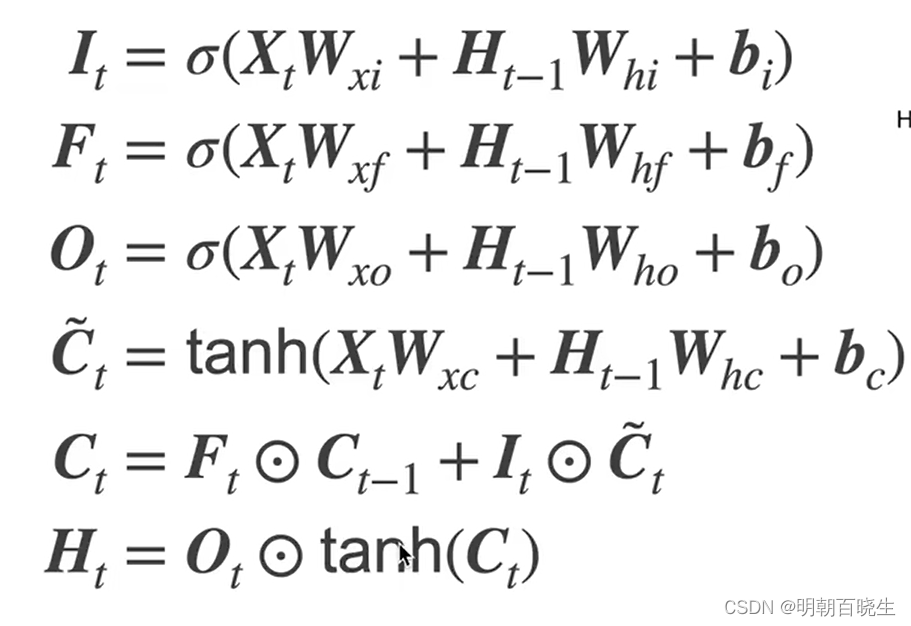
我们最后发现:
的维度必须一致,都是hidden_size
通过,则
最后一个维度也必须是hidden_size
# -*- coding: utf-8 -*-
"""
Created on Thu Aug 3 15:11:19 2023@author: chengxf2
"""# -*- coding: utf-8 -*-
"""
Created on Wed Aug 2 15:34:25 2023@author: chengxf2
"""import torch
from torch import nn
from d21 import torch as d21def normal(shape,devices):data = torch.randn(size= shape, device=devices)*0.01return datadef get_lstm_params(input_size, hidden_size,categorize_size,devices):#隐藏门参数W_xf= normal((input_size, hidden_size), devices)W_hf = normal((hidden_size, hidden_size),devices)b_f = torch.zeros(hidden_size,devices)#输入门参数W_xi= normal((input_size, hidden_size), devices)W_hi = normal((hidden_size, hidden_size),devices)b_i = torch.zeros(hidden_size,devices)#输出门参数W_xo= normal((input_size, hidden_size), devices)W_ho = normal((hidden_size, hidden_size),devices)b_o = torch.zeros(hidden_size,devices)#临时记忆单元W_xc= normal((input_size, hidden_size), devices)W_hc = normal((hidden_size, hidden_size),devices)b_c = torch.zeros(hidden_size,devices)#最终分类结果参数W_hq = normal((hidden_size, categorize_size), devices)b_q = torch.zeros(categorize_size,devices)params =[W_xf,W_hf,b_f,W_xi,W_hi,b_i,W_xo,W_ho,b_o,W_xc,W_hc,b_c,W_hq,b_q]for param in params:param.requires_grad_(True)return paramsdef init_lstm_state(batch_size, hidden_size, devices):cell_init = torch.zeros((batch_size, hidden_size),device=devices)hidden_init = torch.zeros((batch_size, hidden_size),device=devices)return (cell_init, hidden_init)def lstm(inputs, state, params):[W_xf,W_hf,b_f,W_xi,W_hi,b_i,W_xo,W_ho,b_o,W_xc,W_hc,b_c,W_hq,b_q] = params (H,C) = stateoutputs= []for x in inputs:#input gateI = torch.sigmoid((x@W_xi)+(H@W_hi)+b_i)F = torch.sigmoid((x@W_xf)+(H@W_hf)+b_f)O = torch.sigmoid((x@W_xo)+(H@W_ho)+b_o)C_tmp = torch.tanh((x@W_xc)+(H@W_hc)+b_c)C = F*C+I*C_tmpH = O*torch.tanh(C)Y = (H@W_hq)+b_qoutputs.append(Y)return torch.cat(outputs, dim=0),(H,C)def main():batch_size,num_steps =32, 35train_iter, cocab= d21.load_data_time_machine(batch_size, num_steps)if __name__ == "__main__":main()参考
CSDN
https://www.cnblogs.com/pinard/p/6519110.html
57 长短期记忆网络(LSTM)【动手学深度学习v2】_哔哩哔哩_bilibili
相关文章:
[PyTorch][chapter 46][LSTM -1]
前言: 长短期记忆网络(LSTM,Long Short-Term Memory)是一种时间循环神经网络,是为了解决一般的RNN(循环神经网络)存在的长期依赖问题而专门设计出来的。 目录: 背景简介 LSTM C…...
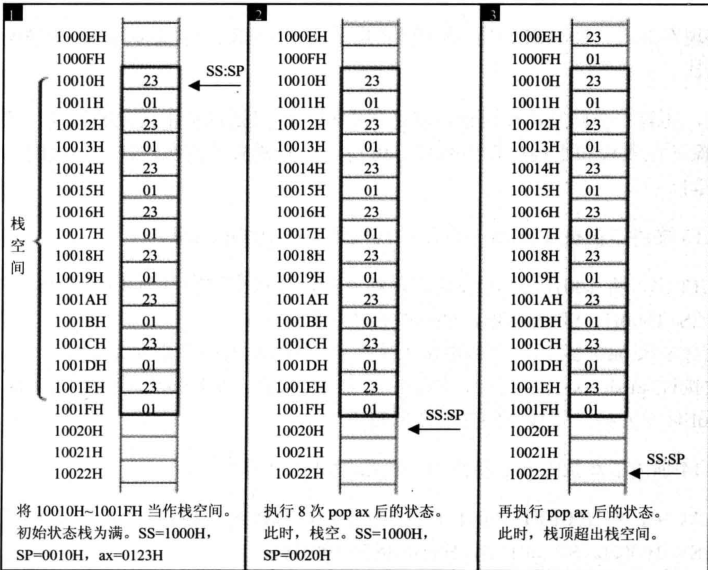
寄存器详解(二)
目录 内存中字的存储 示例: 数据段寄存器DS与[address] 字的传送 数据段简介 CPU提供的栈机制 栈段寄存器SS和栈顶指针寄存器SP PUSH AX指令的完整描述 示例图 POP AX指令的完整描述 示例图 栈顶超界问题 示例一: 示例二: 内存中字…...

Java AIO
在Java中,AIO代表异步I/O(Asynchronous I/O),它是Java NIO的一个扩展,提供了更高级别的异步I/O操作。AIO允许应用程序执行非阻塞I/O操作,而无需使用Selector和手动轮询事件的方式。 与传统的NIO和Java NIO…...

java集合总结
1.常见集合 Collection List:有序可重复集合,可直接根据元素的索引来访问 Vector-StackArrayListLinkedList Queue:队列集合 Deque-LinkedList、ArrayDequePriorityQueue Set:无序不可重复集合,只能根据元素本身来访问…...

list交并补差集合
list交并补差集合 工具类依赖 <dependency><groupId>org.apache.commons</groupId><artifactId>commons-lang3</artifactId><version>3.8.1</version> </dependency><dependency><groupId>commons-collections&…...

【微信小程序】父组件修改子组件数据或调用子组件方法
一、使用场景 页面中用到了自定义组件形成父子组件关系,在父组件某个特定时期想要操作子组件中的数据或方法,比如离开页面的时候清空子组件的数据。 二、方法 父组件可以通过this.selectComponent方法获取子组件实例对象,这样就可以直接访…...

frp通过nginx映射multipart/x-mixed-replace; boundary=frame流媒体出外网访问
要通过Nginx访问multipart/x-mixed-replace流媒体协议,并通过FRP进行映射访问,你可以按照以下步骤进行操作: 配置Nginx以支持multipart/x-mixed-replace流媒体协议。你需要编辑Nginx的配置文件(通常是nginx.conf)&…...
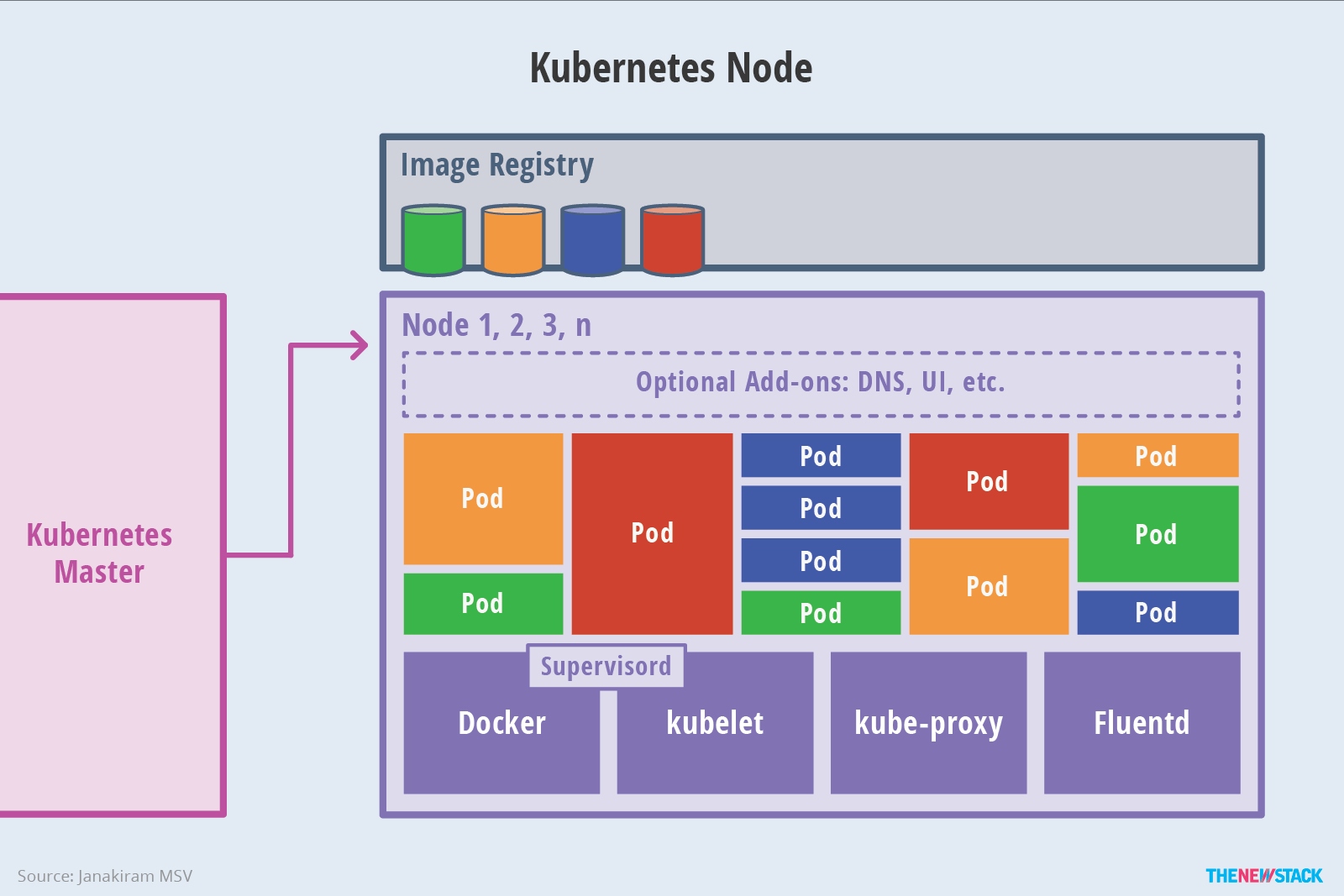
Kubernetes概述
Kubernetes概述 使用kubeadm快速部署一个k8s集群 Kubernetes高可用集群二进制部署(一)主机准备和负载均衡器安装 Kubernetes高可用集群二进制部署(二)ETCD集群部署 Kubernetes高可用集群二进制部署(三)部署…...

Jmeter教程
目录 安装与配置 一:下载jdk——配置jdk环境变量 二:下载JMeter——配置环境变量 安装与配置 一:下载jdk——配置jdk环境变量 1.新建环境变量变量名:JAVA_HOME变量值:(即JDK的安装路径) 2.编辑Path%J…...

用Rust实现23种设计模式之建造者模式
当使用 Rust 实现建造者模式时,我们可以通过结构体和方法链来实现。建造者模式是一种创建型设计模式,它允许你按照特定的顺序构建复杂对象,同时使你能够灵活地构建不同的变体。下面是一个使用 Rust 实现建造者模式的示例, 在示例中…...

聚观早报 | 腾讯字节等企业驰援防汛救灾;新能源车7月销量单出炉
【聚观365】8月4日消息 腾讯字节等企业驰援防汛救灾新能源车7月销量成绩单出炉Model Y等车型低温续航衰减严重华为Mate60系列猜想图曝光支付宝做短视频引来羊毛党 腾讯字节等企业驰援防汛救灾 近日,京津冀地区遭遇极端降雨天气,引发洪涝和地质灾害&…...
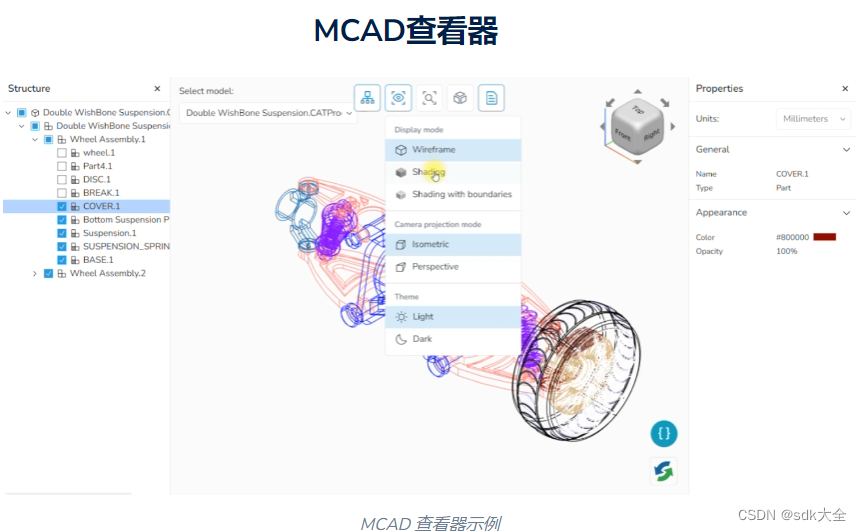
Crack:CAD Exchanger SDK 3.20 Web Toolkit 应用
在CAD Exchanger SDK 版本 3.20.0中,我们在 Web Toolkit 中包含了绘图、BIM 和 MCAD 查看器的示例,以展示如何使用每个工具可视化数据。这些查看器具有显示不同类型数据的特定功能,允许用户根据自己的需求单独使用它们。我们将继续增强每个查…...

改造 ChatGPT-Next-Web 项目重新生成 Docker 镜像
改造 ChatGPT-Next-Web 项目重新生成 Docker 镜像 0.背景1. 修改代码2. 生成 Docker 镜像3. 上传 Docker 镜像4. 运行 Docker 镜像 0.背景 需要通过 ChatGPT-Next-Web 使用自己搭建的 OpenAI API 兼容的服务器,需要对 ChatGPT-Next-Web 项目的少量代码进行改造。 …...

git修改commit日志
由于公司对版本提交日志进行检查,如果不符合要求,则push失败。 以下是修改commit日志的方法: 1.进入到提交代码文件所在目录,即git所在目录下 cd app-repository 2.git log git log commit bf29e3e5e799d364fe2975677baf18c9…...
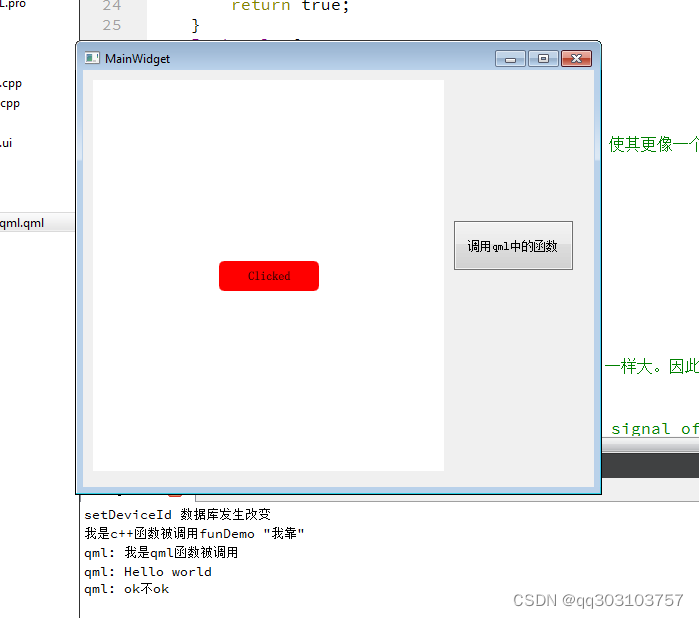
Qt之qml和widget混合编程调用
首先是创建一个widget项目 然后需要添加qml和quick的插件使用 QT quickwidgets qml 接着要在界面上创建一个quickwidget和按钮 创建一个c对象类 QObjectQml #ifndef QOBJECTQML_H #define QOBJECTQML_H#include <QObject> #include <QDebug> class QObjectQml …...

深度学习torch基础知识
torch. detach()拼接函数torch.stack()torch.nn.DataParallel()np.clip()torch.linspace()PyTorch中tensor.repeat()pytorch索引查找 index_select detach() detach是截断反向传播的梯度流 将某个node变成不需要梯度的Varibale。因此当反向传播经过这个node时,梯度…...
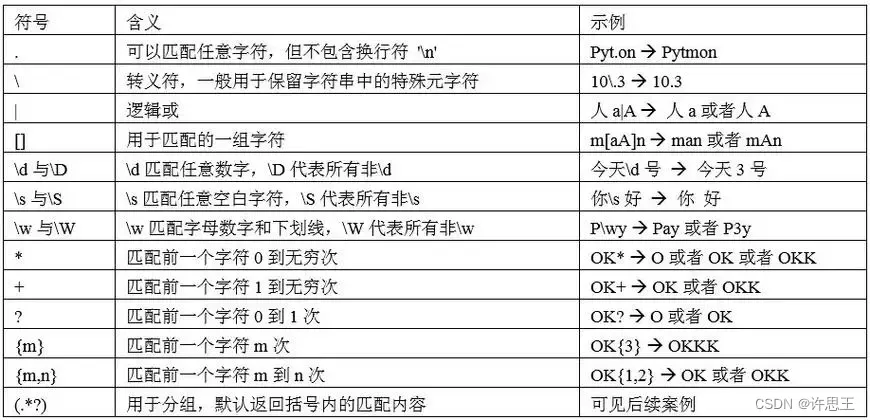
【JAVA】正则表达式是啥?
个人主页:【😊个人主页】 系列专栏:【❤️初识JAVA】 文章目录 前言正则表达式正则表达式语法正则表达式的特点捕获组实例 前言 如果我们想要判断给定的字符串是否符合正则表达式的过滤逻辑(称作“匹配”),…...
网络安全之原型链污染
目录: 目录: 一、概念 二、举例 三、 实操了解 总结 四、抛出原题,历年原题复现 第一题: 五、分析与原理 第二题: 八、分析与原理 九、具体操作,payload与结果 结果: 一、概念 Java…...

【腾讯云Cloud Studio实战训练营】使用Cloud Studio迅捷开发一个3D家具个性化定制应用
目录 前言: 一、腾讯云 Cloud Studio介绍: 1、接近本地 IDE 的开发体验 2、多环境可选,或连接到云主机 3、随时分享预览效果 4、兼容 VSCode 插件 5、 AI代码助手 二、腾讯云Cloud Studio项目实践(3D家具个性化定制应用&…...

【计算机网络】第四章 网络层(一)
文章目录 第四章 网络层4.1 网络层概述4.2 网络层提供的两种服务4.2.1 小结 第四章 网络层 网络层是计算机网络体系结构中的一个关键层,位于传输层上方、数据链路层下方。它负责将传输层提供的数据分割成适当大小的数据包,并在不同网络之间进行路由选择和…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...

C/Python/Go示例 | Socket Programing与RPC
Socket Programming介绍 Computer networking这个领域围绕着两台电脑或者同一台电脑内的不同进程之间的数据传输和信息交流,会涉及到许多有意思的话题,诸如怎么确保对方能收到信息,怎么应对数据丢失、被污染或者顺序混乱,怎么提高…...

uni-app学习笔记二十三--交互反馈showToast用法
showToast部分文档位于uniapp官网-->API-->界面:uni.showToast(OBJECT) | uni-app官网 uni.showToast(OBJECT) 用于显示消息提示框 OBJECT参数说明 参数类型必填说明平台差异说明titleString是提示的内容,长度与 icon 取值有关。iconString否图…...

如何让非 TCP/IP 协议驱动屏蔽 IPv4/IPv6 和 ARP 报文?
——从硬件过滤到协议栈隔离的完整指南 引言 在现代网络开发中,许多场景需要定制化网络协议(如工业控制、高性能计算),此时需确保驱动仅处理特定协议,避免被标准协议(如 IPv4/IPv6/ARP)干扰。本文基于 Linux 内核驱动的实现,探讨如何通过硬件过滤、驱动层拦截和协议栈…...




