数学建模学习(7):Matlab绘图
一、二维图像绘制
1.绘制曲线图
最基础的二维图形绘制方法:plot
-plot命令自动打开一个图形窗口Figure; 用直线连接相邻两数据点来绘制图形
-根据图形坐标大小自动缩扩坐标轴,将数据标尺及单位标注自动加到两个坐标轴上,可自定坐标轴,可把x, y 轴用对数坐标表示
-如果已经存在一个图形窗口,plot命令则清除当前图形,绘制新图形
可单窗口单曲线绘图;可单窗口多曲线绘图;可单窗口多曲线分图绘图;可多窗口绘图
-可任意设定曲线颜色和线型;可给图形加坐标网线和图形加注功能


绘制单条曲线
x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y)
绘制多条曲线
x = linspace(-2*pi,2*pi);
y1 = sin(x);
y2 = cos(x);
plot(x,y1,x,y2)

绘制多条曲线(利用矩阵)
将矩阵的每一列绘制为单独的线条
Y = magic(4);
plot(Y)
指定线型
x = 0:pi/100:2*pi;
y1 = sin(x);
y2 = sin(x-0.25);
y3 = sin(x-0.5);
plot(x,y1,x,y2,'--',x,y3,':')
指定标记
x = 0:pi/10:2*pi;
y1 = sin(x);
y2 = sin(x-0.25);
y3 = sin(x-0.5);
plot(x,y1,'g',x,y2,'b--o',x,y3,'c*')
指定标记(在特定的点处)
x = linspace(0,10);
y = sin(x);
plot(x,y,'-o','MarkerIndices',1:5:length(y))
指定线宽、标记大小和标记颜色
x = -pi:pi/10:pi;
y = tan(sin(x)) - sin(tan(x));
plot(x,y,'--gs',...
'LineWidth',2,...
'MarkerSize',10,...
'MarkerEdgeColor','b',...
'MarkerFaceColor',[0.5,0.5,0.5])
线型查找表
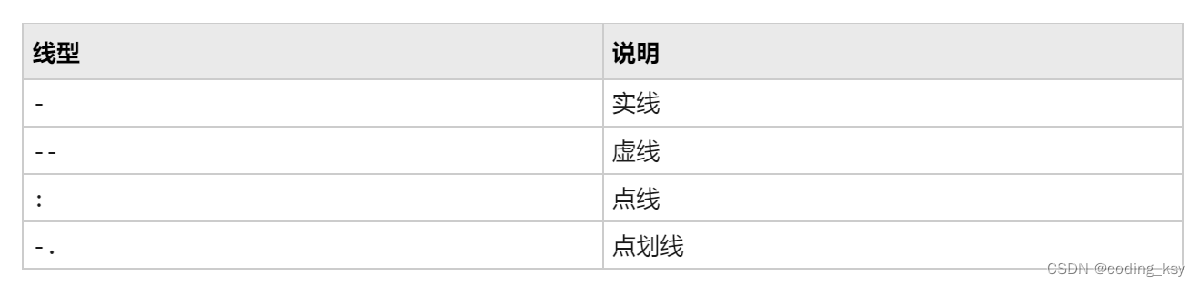
标记查找表

颜色查找表
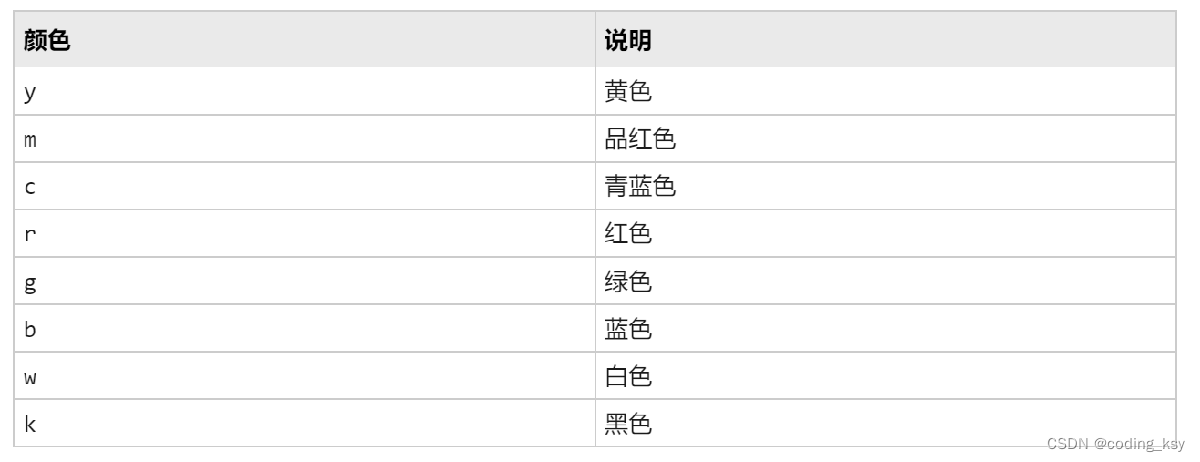
*交叉知识-更改颜色的Color方法
对于自定义颜色,请指定 RGB 三元组或十六进制颜色代码。
1.RGB 三元组是包含三个元素的行向量,其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于 [0,1] 范围内,例如 [0.4 0.6 0.7]。
2.十六进制颜色代码是字符向量或字符串标量,以井号 (#) 开头,后跟三个或六个十六进制数字,范围可以是 0 到 F。这些值不区分大小写。因此,颜色代码 '#FF8800' 与 '#ff8800'、'#F80' 与 '#f80' 是等效的。
组合标记
在 LineSpec 中可对线性/颜色/标记进行同时指定
对于线性/颜色/标记的组合,其是顺序无关的,可随意排列
注意上述参数都是对曲线进行操作的,如果想更改标记颜色,需利用 Marker 系列参数
添加标题和轴标签
x = linspace(0,10,150);
y = cos(5*x);
plot(x,y,'Color',[0,0.7,0.9])
title('2-D Line Plot')
xlabel('x')
ylabel('cos(5x)')
绘制持续时间并指定刻度格式
t = 0:seconds(30):minutes(3);
y = rand(1,7);
plot(t,y,'DurationTickFormat','mm:ss')
*交叉知识-hold方法
hold on 保留当前坐标区中的绘图,从而使新添加到坐标区中的绘图不会删除现有绘图。MATLAB将调整坐标区的范围、刻度线和刻度标签以显示完整范围的数据。如果不存在坐标区,hold 命令会创建坐标区。
hold off 将保留状态设置为 off,从而使新添加到坐标区中的绘图清除现有绘图并重置所有的坐标区属性。添加到坐标区的下一个绘图基于坐标区的 ColorOrder 和 LineStyleOrder 属性使用第一个颜色和线型。此选项为默认行为。
x = linspace(-pi,pi);
y1 = sin(x);
plot(x,y1)
hold on
y2 = cos(x);
plot(x,y2)
hold off
2. 绘制散点图

创建散点图
x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);
scatter(x,y)
改变点的大小
x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);
sz = linspace(1,100,200);
scatter(x,y,sz)
scatter(x,y,1)
scatter(x,y,10)
scatter(x,y,abs(y))
改变点的颜色
x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);
c = linspace(1,10,length(x));
scatter(x,y,[],c)

改变点的填充
x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);
sz = 25;
c = linspace(1,10,length(x));
scatter(x,y,sz,c,'filled')
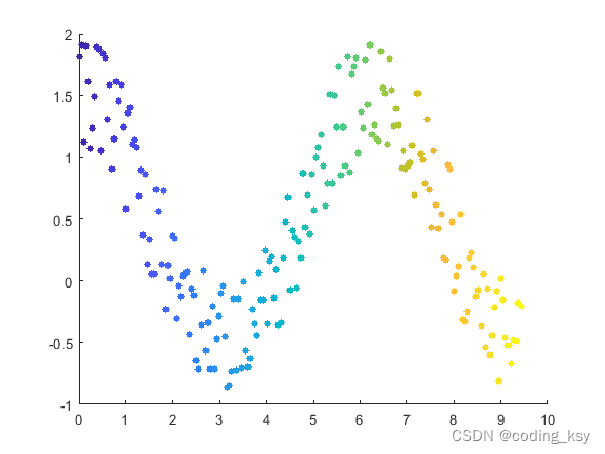
改变标记符号
theta = linspace(0,2*pi,150);
x = sin(theta) + 0.75*rand(1,150);
y = cos(theta) + 0.75*rand(1,150);
sz = 140;
scatter(x,y,sz,'d')
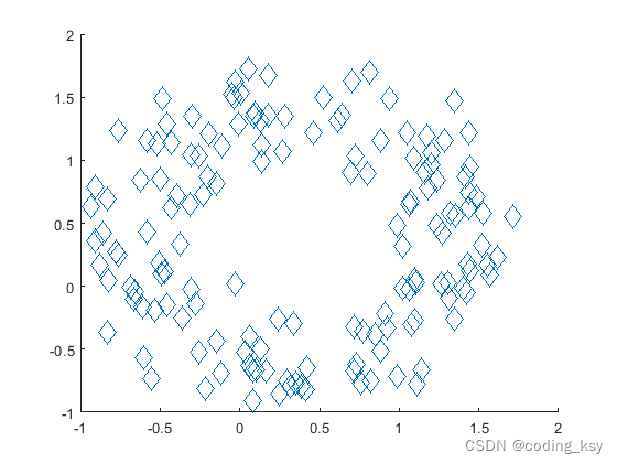
3. 绘制直方图

创建直方图
y = [75 91 105 123.5 131 150 179 203 226 249 281.5];
bar(y)
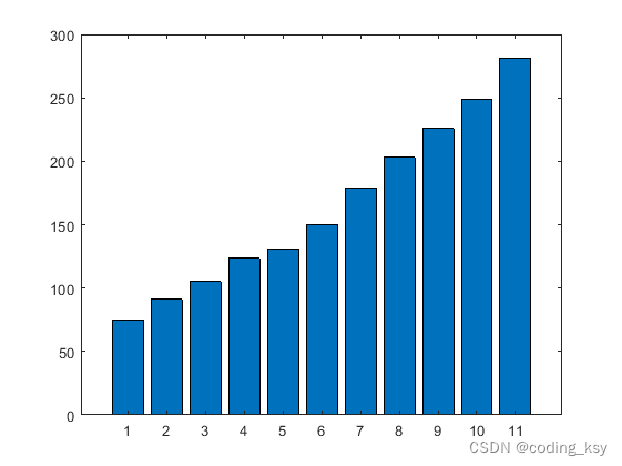
堆叠直方图
x = [1980 1990 2000];
y = [15 20 -5; 10 -17 21; -10 5 15];
bar(x,y,'stacked')
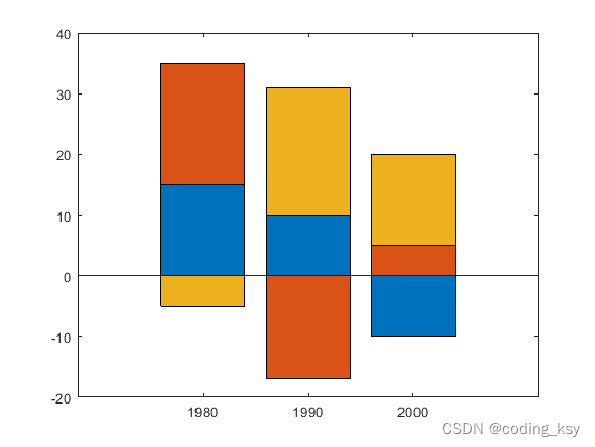
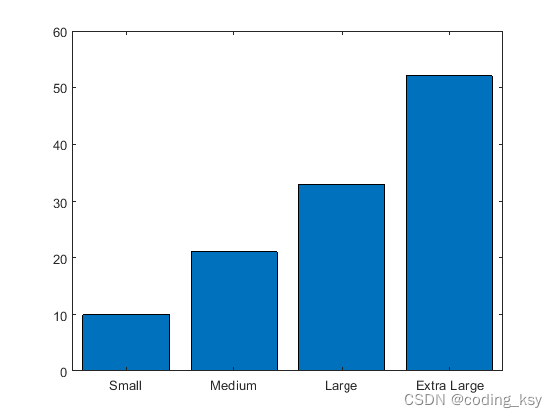
更改横坐标
X = categorical({'Small','Medium','Large','Extra Large'});
X = reordercats(X,{'Small','Medium','Large','Extra Large'});
Y = [10 21 33 52];
bar(X,Y)
4. 绘制统计图
根据数据的分布做统计直方图(老版本为hist,新版本为histogram)

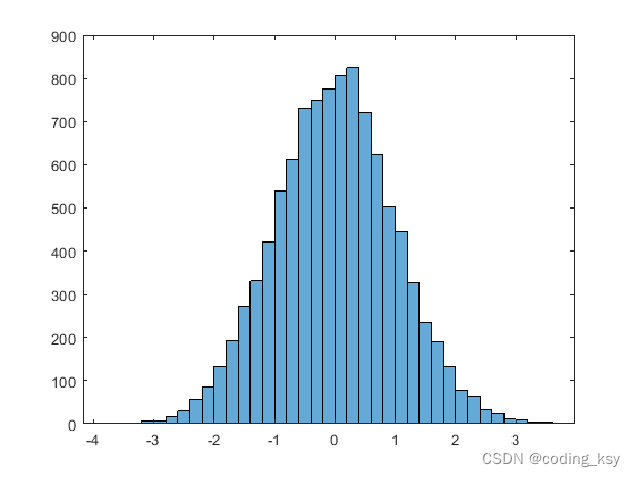
创建统计图
x = randn(10000,1);
histogram(x)
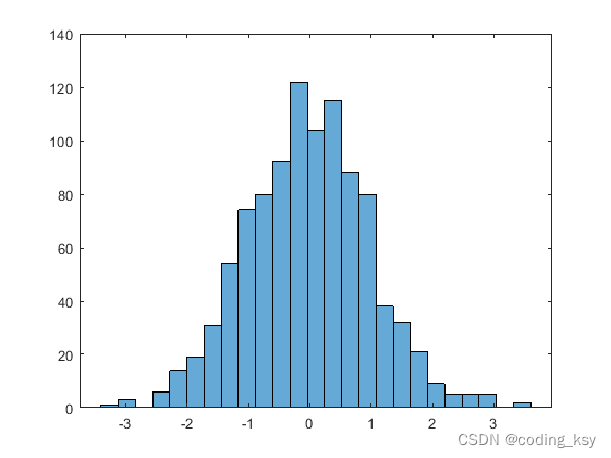
更改直方个数
x = randn(1000,1);
nbins = 25;
histogram(x,nbins
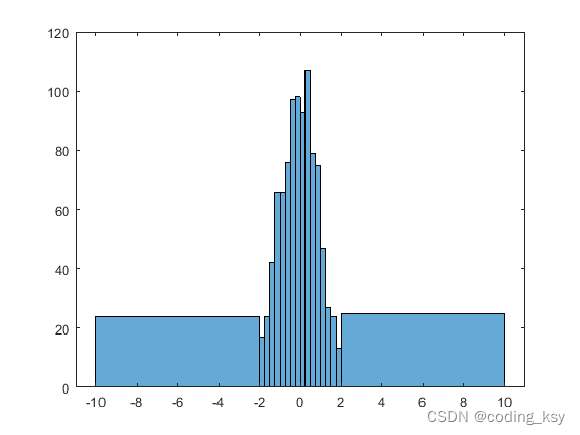
指定每个直方柱对应的范围
x = randn(1000,1);
edges = [-10 -2:0.25:2 10];
histogram(x,edges);
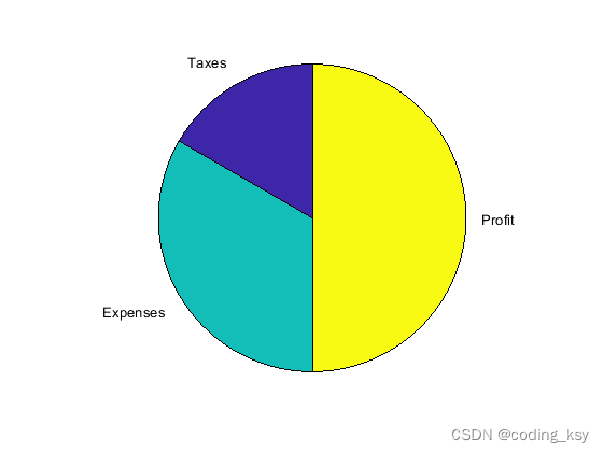
5. 绘制饼状图

创建饼状图
X = 1:3;
labels = {'Taxes','Expenses','Profit'};
pie(X,labels)
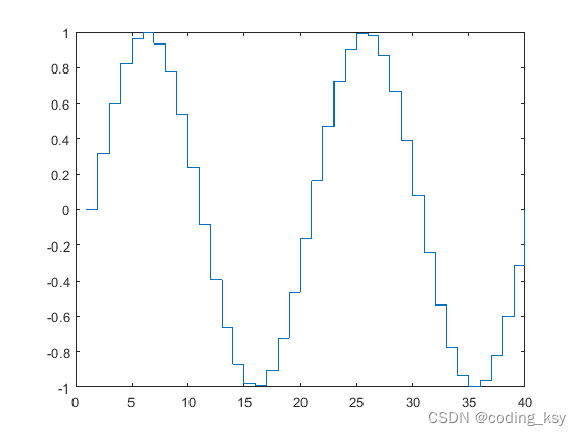
6. 绘制阶梯图

创建阶梯图
X = linspace(0,4*pi,40);
Y = sin(X);
stairs(Y)
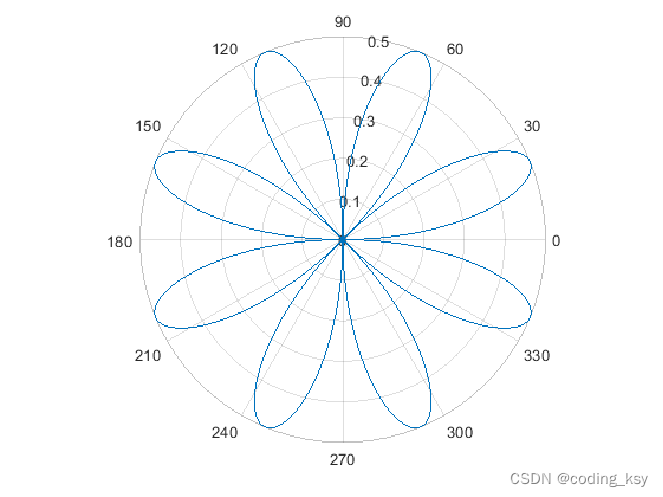
7. 绘制极坐标图

创建极坐标图
theta = 0:0.01:2*pi;
rho = sin(2*theta).*cos(2*theta);
polarplot(theta,rho)
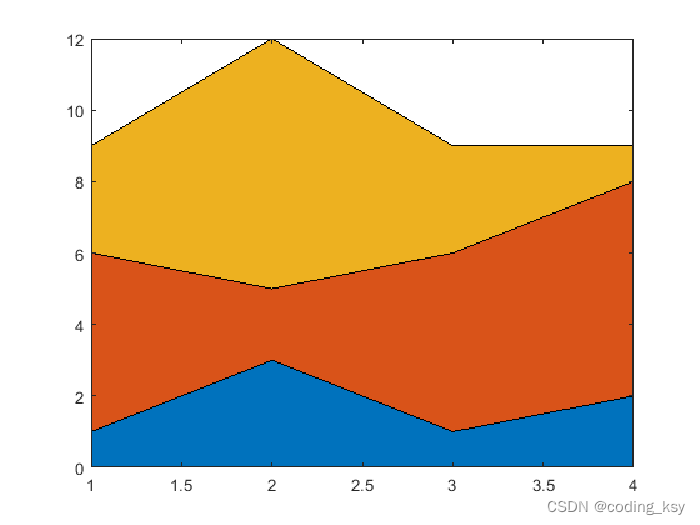
8. 绘制区域图

创建极区域图
Y = [1 5 3; 3 2 7; 1 5 3; 2 6 1];
area(Y)
*交叉知识-子窗口
subplot(m,n,p) 将当前图窗划分为 m×n 网格,并在 p 指定的位置创建坐标区。MATLAB 按行号对子图位置进行编号。第一个子图是第一行的第一列,第二个子图是第一行的第二列,依此类推。如果指定的位置已存在坐标区,则此命令会将该坐标区设为当前坐标区。
*若mnp均为一位数时,逗号可忽略
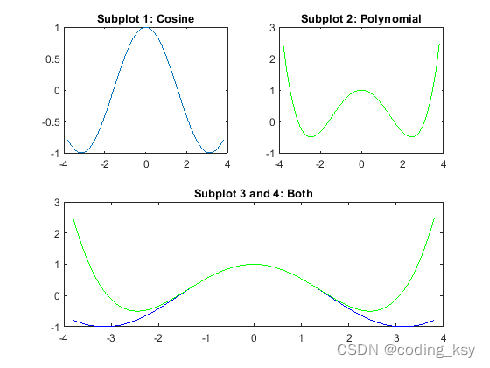
subplot(2,2,1);
x = linspace(-3.8,3.8);
y_cos = cos(x);
plot(x,y_cos);title('Subplot 1: Cosine')
subplot(2,2,2);
y_poly = 1 - x.^2./2 + x.^4./24;
plot(x,y_poly,'g');title('Subplot 2: Polynomial')
subplot(2,2,[3,4]);
plot(x,y_cos,'b',x,y_poly,'g');title('Subplot 3 and 4: Both')
二、三维图像的绘制
0. 从二维延拓
大部分二维图形提供了像三维延拓的方法

1. 绘制曲线图(3d)

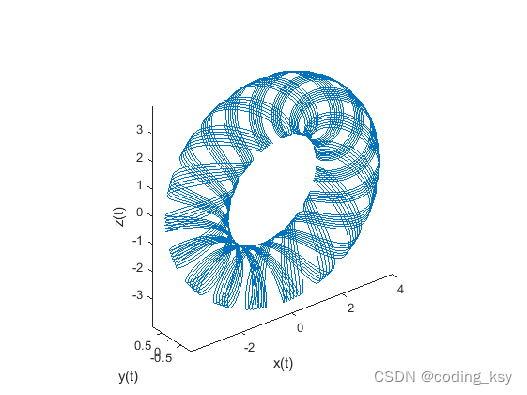
创建三维曲线图
t = 0:pi/500:40*pi;
xt = (3 + cos(sqrt(32)*t)).*cos(t);
yt = sin(sqrt(32) * t);
zt = (3 + cos(sqrt(32)*t)).*sin(t);
plot3(xt,yt,zt)
axis equal
xlabel('x(t)')
ylabel('y(t)')
zlabel('z(t)')
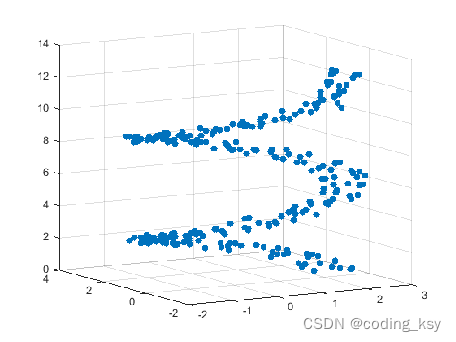
创建三维散点图
z = linspace(0,4*pi,250);
x = 2*cos(z) + rand(1,250);
y = 2*sin(z) + rand(1,250);
scatter3(x,y,z,'filled')
scatter3(x,y,z,'filled')
scatter3(x,y,z,abs(z)+1,'filled')
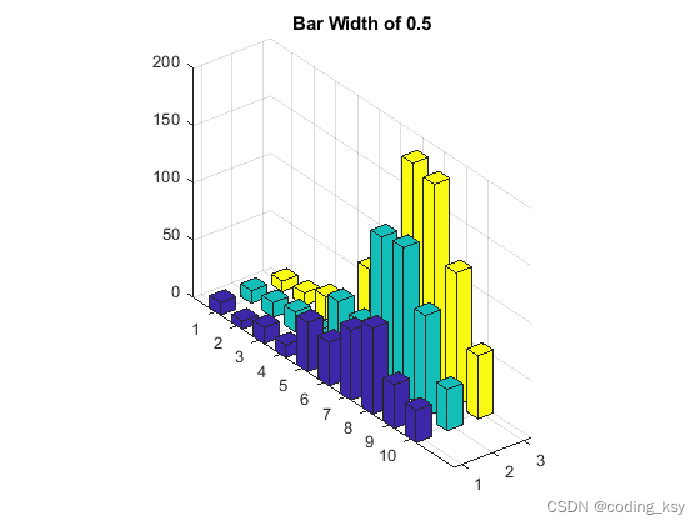
3. 绘制直方图(3d)

创建三维直方图
load count.dat
Z = count(1:10,:);
width = 0.5;
bar3(Z,width)
title('Bar Width of 0.5')

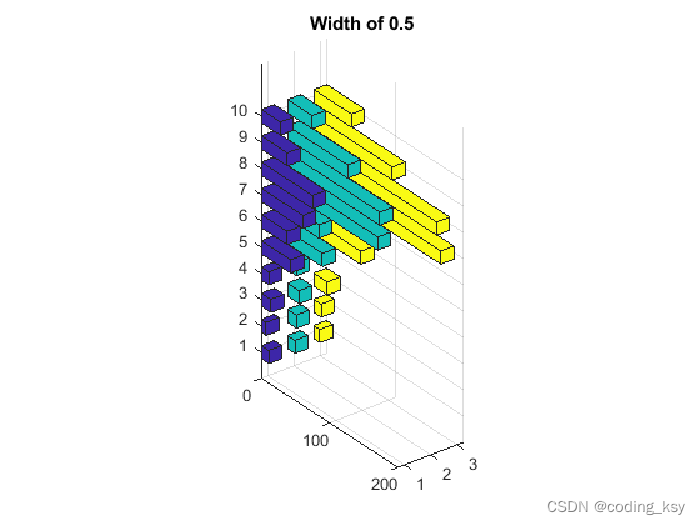
创建水平三维直方图
load count.dat;
Y = count(1:10,:);
width = 0.5;
figure
bar3h(Y,width)
title('Width of 0.5')
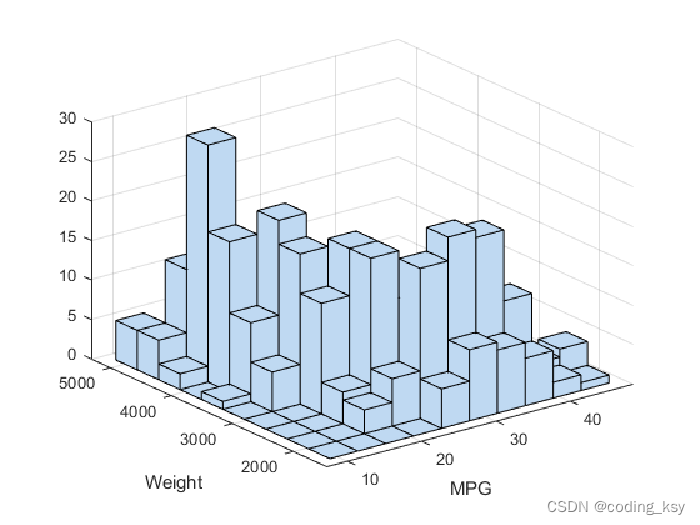
4. 绘制统计图(3d)

创建三维统计图
load carbig
X = [MPG,Weight];
hist3(X)
xlabel('MPG')
ylabel('Weight')
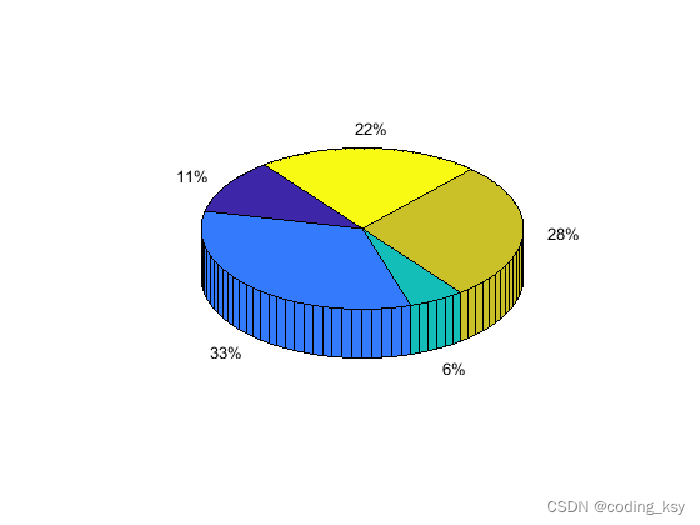
5. 绘制饼状图(3d)

创建三维饼状图
x = [1,3,0.5,2.5,2];
pie3(x)
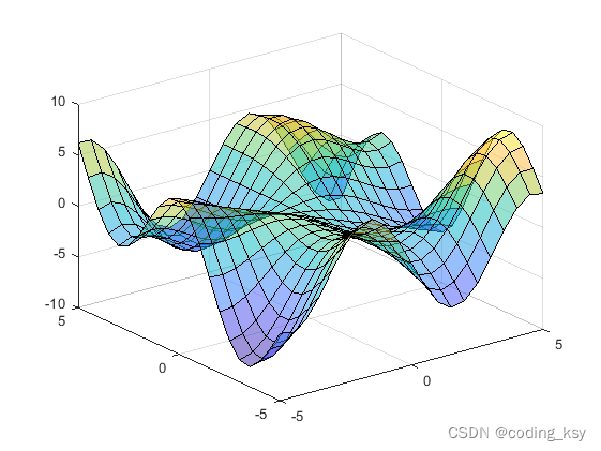
6. 绘制曲面图

创建三维曲面图
[X,Y] = meshgrid(-5:.5:5);
Z = Y.*sin(X) - X.*cos(Y);
s = surf(X,Y,Z,'FaceAlpha',0.5)
7. 绘制网格曲面图

修改边界
[X,Y] = meshgrid(-8:.5:8);
R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R)./R;
mesh(X,Y,Z)
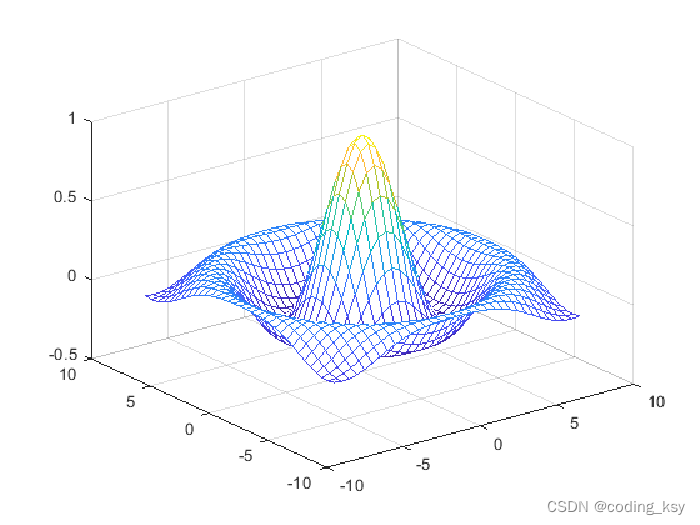
*交叉知识-mesh/surf
[X,Y] = meshgrid(-8:.5:8);R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R)./R;
subplot(121)
mesh(X,Y,Z)
subplot(122)
surf(X,Y,Z)
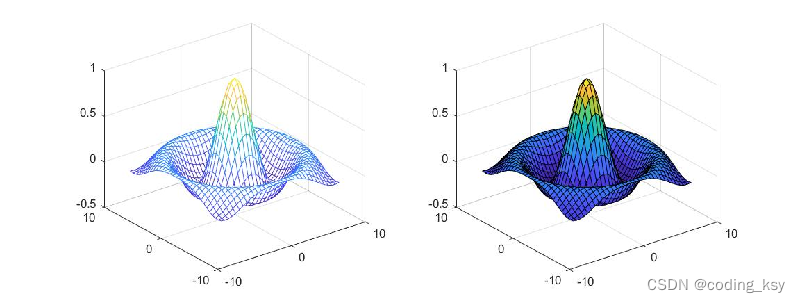
mesh:采用彩色的线条为基础,在其中填补白色的面
surf: 采用彩色的面为基础,在其中填补黑色的线条
*交叉知识-任意散点作图
利用griddata函数拟合均匀曲面
load('Point.mat')
x=A(:,1);y=A(:,2);z=A(:,3);
[X,Y,Z]=griddata(x,y,z,linspace(min(x),max(x))',linspace(min(y),max( y)),'v4’);
surf(X,Y,Z)
8. 绘制等高线图

创建三维曲面图
x = -2:0.2:2;
y = -2:0.2:3;
[X,Y] = meshgrid(x,y);
Z = X.*exp(-X.^2-Y.^2);
contour(X,Y,Z,'ShowText','on')
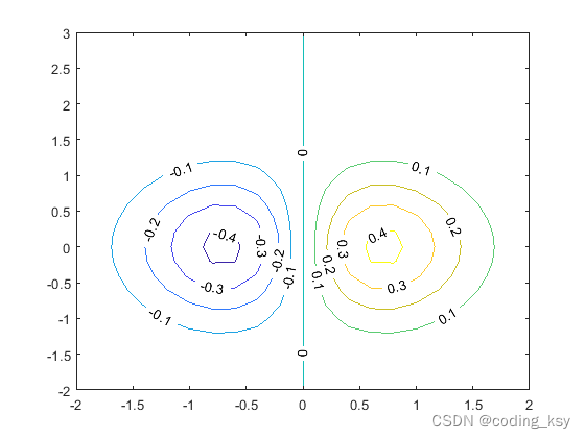
*交叉知识-view方法
当等高线图无法反映出图像的全部细节时,可采用view方法进行投影
[X,Y,Z] = peaks;
subplot(121)
surf(X,Y,Z)
subplot(122)
surf(X,Y,Z)
view(2)

View可在保留色彩的同时,将三维图投影至X-Y平面
*交叉知识-绘图常用指令

三、句柄/窗口控制
1. 句柄方法
通过句柄可以对图像的参数进行一些后期修改
x = linspace(-2*pi,2*pi);
y1 = sin(x);
y2 = cos(x);
p = plot(x,y1,x,y2);
p(1).LineWidth = 2;
p(2).Marker = '*';
通过建立图像句柄,对第一条曲线的线宽与第二条曲线的标识进行修改
*句柄能调用的特性,必须是图像所拥有的特性
- gcf 返回当前Figure 对象的句柄值
- gca 返回当前axes 对象的句柄值
- gco 返回当前鼠标单击的句柄值
plot(0:0.01:10,sin(0:0.01:10))
xlabel('x(mm)')
ylabel('y(mm)')
set(gca,'FontName','Times New Roman','FontSize',14)
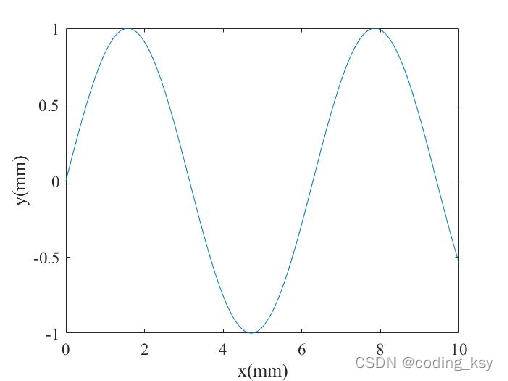
通过建立图像句柄,对图像中的文字进行修改
*注意gca区分子窗口,若采用subplot需对每个sub获取句柄进行操作
*交叉知识-matlab动画
利用gcf读取当前图像窗口,添加至gif
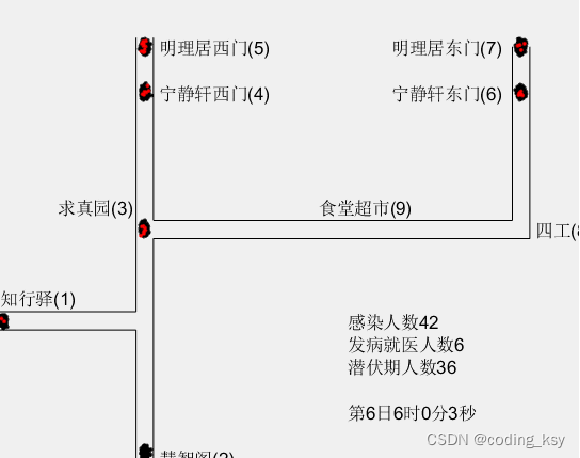
*利用plot绘制直线作为道路
*关闭坐标轴(axis ff)
*利用scatter绘制点作为人员
*利用text添加文字
![]()
clear;clc;
writerObj=VideoWriter('W3','MPEG-4'); loc_exis=zeros(1,7);
writerObj.FrameRate=100;
open(writerObj);
filenames='test.gif';
D=randn(1,100);
for ii = 1:100
scatter(1:ii,D(1:ii))
xlim([1 100])
ylim([-5,5])
drawnow
frame = getframe;
im=frame2im(frame);
[A,mao]=rgb2ind(im,256);
writeVideo(writerObj,frame);
if ii==1
imwrite(A,mao,filenames,'gif','LoopCount',Inf,'DelayTime',0.01);
else
imwrite(A,mao,filenames,'gif','WriteMode','append','DelayTime',0.01);
end
end
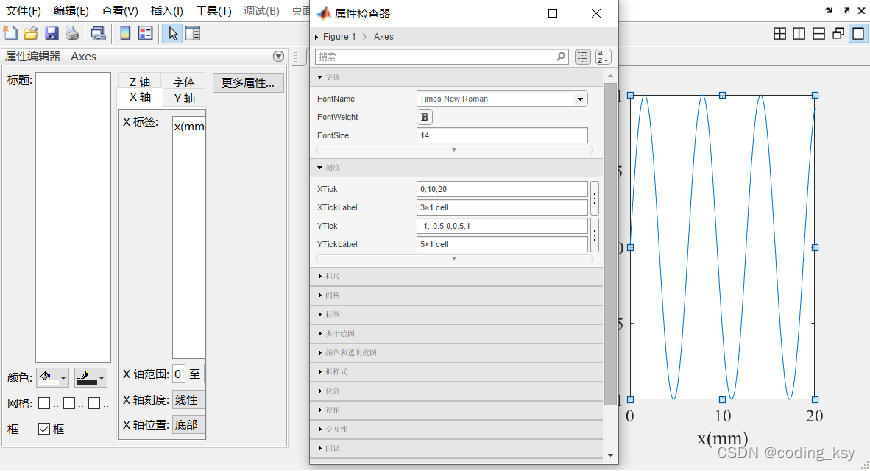
2. 窗口控制
直接通过图像窗口对图像进行修改
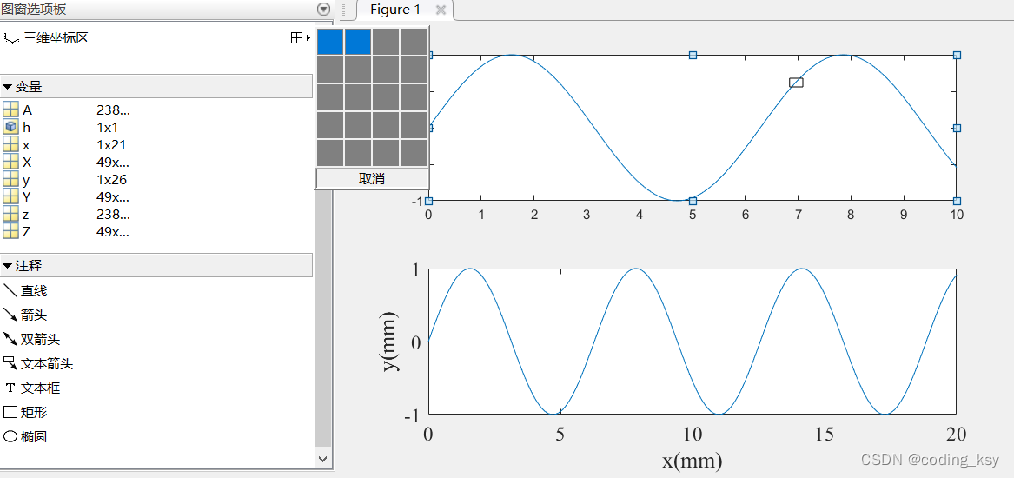
图窗选项板:可进行子图控制,添加箭头等特殊标识
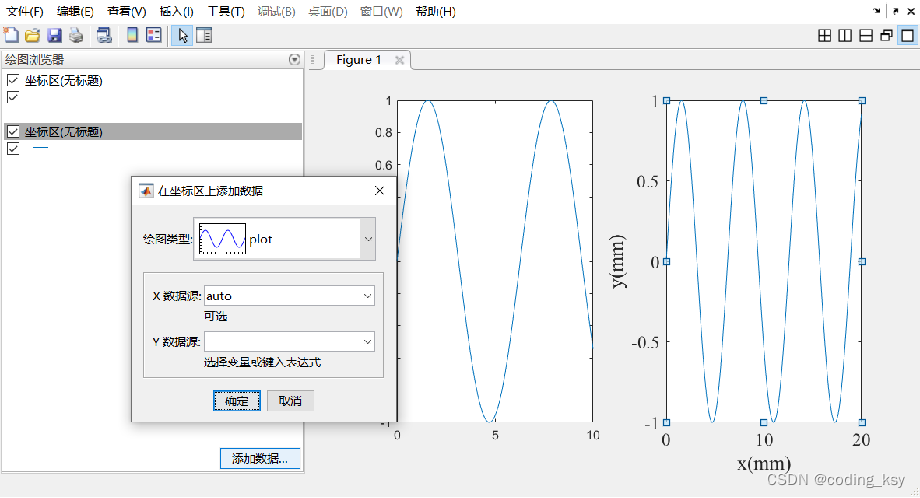
绘图浏览器:可直接添加和删除绘图曲线或点云等元素
属性编辑器:对图像所拥有的元素(线宽、颜色等)手动修改
图窗选项板
相关文章:

数学建模学习(7):Matlab绘图
一、二维图像绘制 1.绘制曲线图 最基础的二维图形绘制方法:plot -plot命令自动打开一个图形窗口Figure; 用直线连接相邻两数据点来绘制图形 -根据图形坐标大小自动缩扩坐标轴,将数据标尺及单位标注自动加到两个坐标轴上,可自定…...
CSS中所有选择器详解
文章目录 一、基础选择器1.标签选择器2.类选择器3.id选择器4.通配符选择器 二、复合选择器1.交集选择器2.并集选择器 三、属性选择器1.[属性]2.[属性属性值]3.[属性^属性值]4.[属性$属性值]5.[属性*属性值] 四、关系选择器1.父亲>儿子2.祖先 后代3.兄弟4.兄~弟 五、伪类选择…...

STM32 低功耗学习
STM32 电源系统结构介绍 电源系统:VDDA供电区域、VDD供电区域、1.8V供电区域、后备供电区域。 器件的工作电压(VDD)2.0~3.6V 为了提高转换精度,给模拟外设独立供电。电压调节器为1.8V供电区域供电,且1.8V供电区域是电…...

HCIP--云计算题库 V5.0版本
在国家政策的支持下,我国云计算应用市场发展明显加快,越来越多的企业开始介入云产业,出现了大量的应用解决方案,云应用的成功案例逐渐丰富,用户了解和认可程度不断提高,云计算产业发展迎来了“黄金机遇期”…...
小白到运维工程师自学之路 第六十五集 (docker-compose)
一、概述 Docker Compose 的前身是 Fig,它是一个定义及运行多个 Docker 容器的工具。可以使用YAML文件来配置应用程序的服务。然后,使用单个命令,您可以创建并启动配置中的所有服务。Docker Compose 会通过解析容器间的依赖关系(…...

量子机器学习
量子机器学习(QML)是结合量子计算和机器学习的交叉领域,旨在利用量子计算的优势来改进机器学习算法的性能。下面是一些有关量子机器学习的学习资源和技术应用: 学术论文和研究资料: ArXiv.org:在ArXiv的量子物理和机器学习类别中&…...
WEB集群——tomcat
1. 简述静态网页和动态网页的区别。 2. 简述 Webl.0 和 Web2.0 的区别。 3. 安装tomcat8,配置服务启动脚本,部署jpress应用。 一、简述静态网页和动态网页的区别 (1)静态网页 1.什么是静态网页 请求响应信息,发…...
Vulnhub: blogger:1靶机
kali:192.168.111.111 靶机:192.168.111.176 信息收集 端口扫描 nmap -A -sC -v -sV -T5 -p- --scripthttp-enum 192.168.111.176 在80端口的/assets/fonts/目录下发现blog目录,访问后发现为wordpress 利用wpscan发现wordpress插件wpdisc…...

老版MFC工程迁移到VC2019编译EXE太大的问题
有个老版静态链接MFC库的MFC程序需要迁移到VC2019编译,直接用VC2019打开就会自动迁移过去,然后编译一下,生成的EXE大小将近3MB,老版的工程编译出来也就600多KB。 肯定哪里不对劲! 好一顿研究之后发现原来默认会把MFC…...
Curve深陷安全事件,OKLink如何破局
出品|欧科云链研究院 作者|Matthew Lee 7月31号,Curve 在平台表示 Vyper 0.2.15 的稳定币池由于编译器的漏洞所以遭到攻击。具体因为重入锁功能的失效,所以黑客可以轻易发动重入攻击,即允许攻击者在单次交易中执行某…...

2023华数杯数学建模思路A题B题C题模型代码分析
目录 一.2023华数杯数学建模最新思路:比赛开始后第一时间更新 更新查看文末名片 二.往年华数杯赛题简介分析: 一.2023华数杯数学建模最新思路:比赛开始后第一时间更新 更新查看文末名片 二.往年华数杯赛题简介分析: 2022华数杯…...
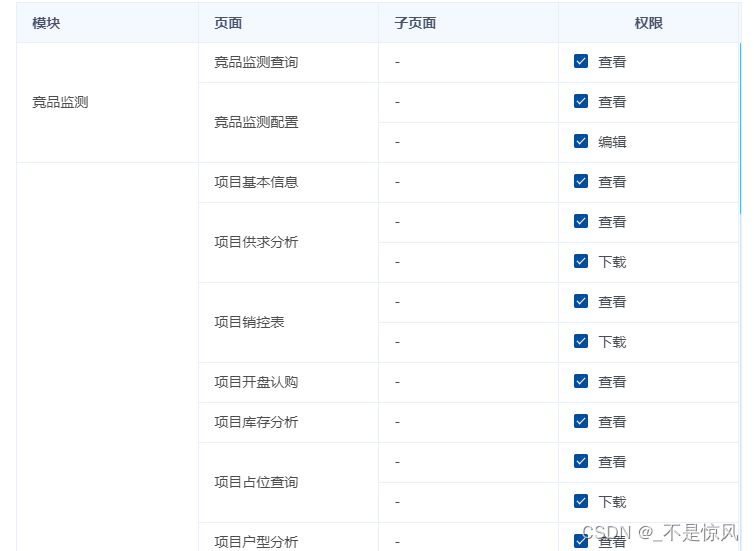
el-table合并单元格
el-tabel数据结构 此处为this.rolePermitItemList 合并后的样式: el-table-column 需要添加property字段,属性值同props,用来判断需要合并的字段 <el-table :data"rolePermitItemList" style"width: calc(100% );margi…...

html5设置不缓存
<meta http-equiv"Cache-Control" content"no-cache, no-store, must-revalidate"> <meta http-equiv"Pragma" content"no-cache"> <meta http-equiv"Expires" content"0"> 使用meta元素的htt…...

kotlin 的函数参数
https://blog.csdn.net/yoonerloop/article/details/123241451 一、无参数的函数参数 1、回调 //定义 interface OnClickListener { fun onClick() } private fun setOnClickListener(listener: OnClickListener) { } //使用 setOnClickListener(object : OnClickLi…...

谈谈 Kafka 的幂等性 Producer
使用消息队列,我们肯定希望不丢消息,也就是消息队列组件,需要保证消息的可靠交付。消息交付的可靠性保障,有以下三种承诺: 最多一次(at most once):消息可能会丢失,但绝…...

Doris(三)-集群部署3个FE+3个BE
前置 1)配置java环境 1st 解压jdk包 unzip jdk1.8.0_171-amd64.zip 2nd 配置环境变量 vim /etc/profile#文末添加JAVA_HOME/data/jdk1.8.0_171-amd64 PATH$JAVA_HOME/bin:$PATHexport PATH JAVA_HOME3rd 启用配置 source /etc/profile 4th 验证 java -versi…...

js沙箱逃逸
目录 一、什么是沙箱(sandbox) 二、沙箱技术的实现 & node.js 2.1简单沙箱程序示例 2.2this.tostring S1: S2: 三、arguments.callee.caller 一、什么是沙箱(sandbox) 在计算机安全性方面,沙箱(沙盒、sanboxÿ…...

振弦传感器信号转换器应用山体滑坡安全监测
振弦传感器信号转换器应用山体滑坡安全监测 随着人类文明的进步,自然灾害对人们的生活和财产安全造成的威胁也越来越大。山体滑坡作为自然灾害中的一种,给人们的生活和财产安全带来了极大的威胁。因此,进行山体滑坡的安全监测显得尤为重要。振…...

Moonbeam新增强大的互操作性功能至波卡生态
波卡上的领先多链开发平台Moonbeam发布适用于平行链间活动的新版本互操作性功能。最新的链更新Runtime 2401,是自Moonbeam上线后的最大更新,其中包括三个针对开发者于链上的里程碑式更新: 用于访问消息传递功能的预编译智能合约从其他波卡平…...
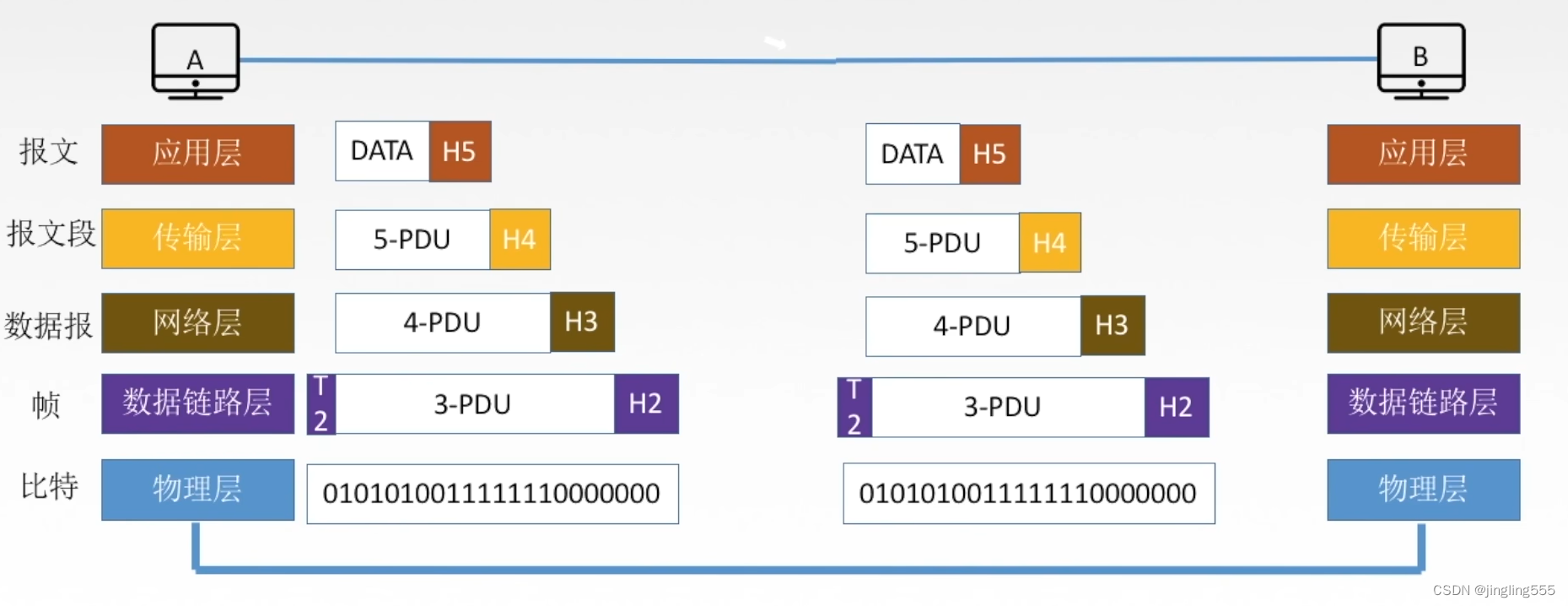
考研408 | 【计算机网络】概述
计算机网络体系结构 计算机网络概述:1.概念,组成,功能,分类2.标准化工作及相关组织3.性能指标体系结构&参考模型:1.分层结构2.协议,接口,服务3.ISO/OSI模型4.TCP/IP模型 目录 计算机网络体…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
