计数排序算法
计数排序
计数排序说明:
计数排序(Counting Sort)是一种非比较性的排序算法,它通过统计元素出现的次数,然后根据元素出现的次数将元素排列在正确的位置上,从而实现排序。计数排序适用于非负整数或者具有确定范围的元素排序,其核心思想是利用一个辅助的计数数组来统计元素出现的次数,并根据次数将元素放置到正确的位置。
以下是计数排序的详细算法原理:
- 找到最大值:首先,我们需要遍历待排序的数组,找到其中的最大值,假设最大值为 k。
- 创建计数数组:接下来,我们创建一个长度为 k+1 的计数数组 count,并将数组中所有元素初始化为 0。计数数组的索引范围是 0 到 k,每个索引对应一个待排序元素的值。
- 统计元素出现次数:遍历待排序的数组,统计每个元素出现的次数,并将统计结果存储在计数数组 count 中。例如,如果数组中有两个元素的值都是 3,那么 count[3] 的值将变为 2。
- 计算累加次数:遍历计数数组 count,计算每个元素在排序后的数组中的累加次数。累加次数表示小于或等于当前元素值的元素个数。具体计算方法是通过累加前一个元素的次数得到当前元素的累加次数。这样,count[i] 就表示在排序后的数组中,小于或等于元素 i 的元素个数。
- 排序:创建一个与待排序数组相同长度的临时数组 sortedArr,用于存储排序结果。然后,遍历待排序数组,根据计数数组 count 中对应元素的累加次数,将每个元素放到正确的位置上。具体做法是找到当前元素在排序后数组中的索引位置,将其放入 sortedArr 数组的相应位置。同时,更新计数数组 count 中对应元素的累加次数,使其减少 1。这样,相同元素的相对顺序会保持不变。
- 完成排序:当遍历完待排序数组后,sortedArr 中就存储了排好序的结果。
计数排序是一种稳定的排序算法,因为相同元素的相对顺序不会改变。它适用于非负整数或者具有确定范围的元素排序,且时间复杂度为 O(n + k),其中 n 是元素个数,k 是待排序元素的最大值。
图解演示:
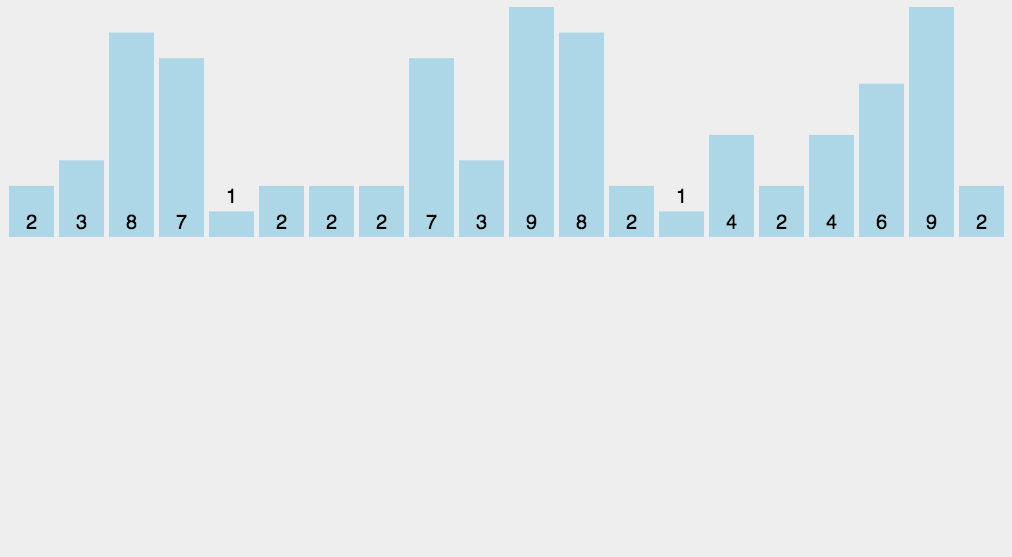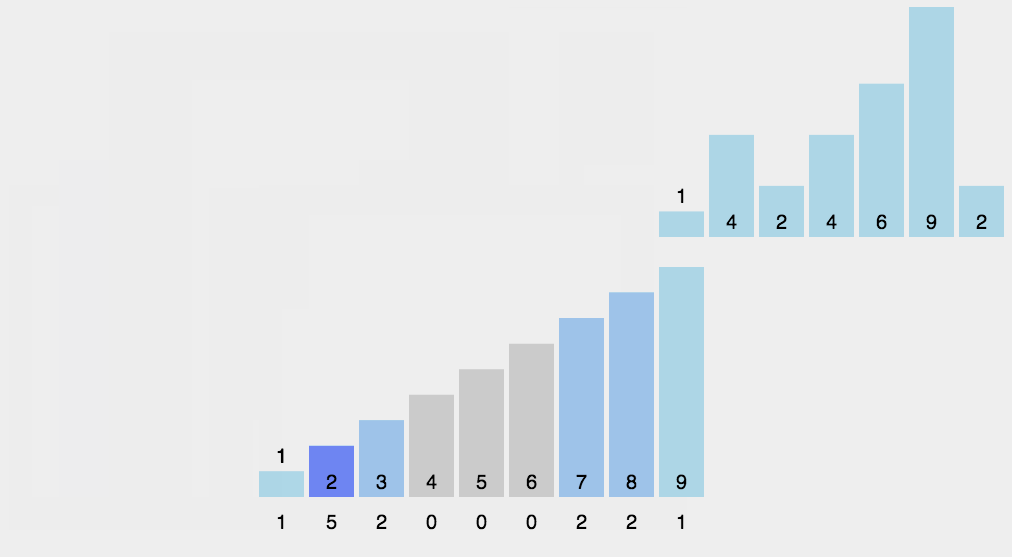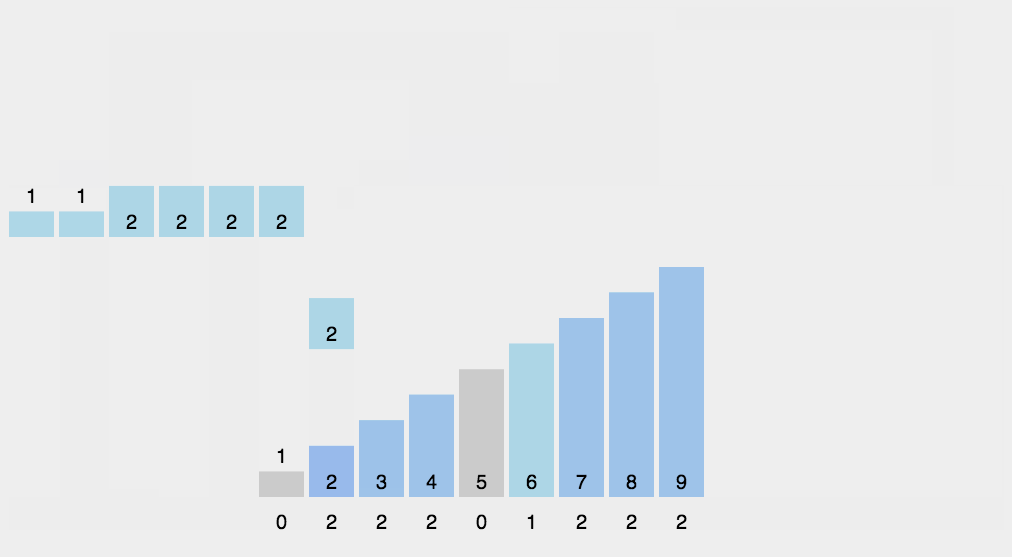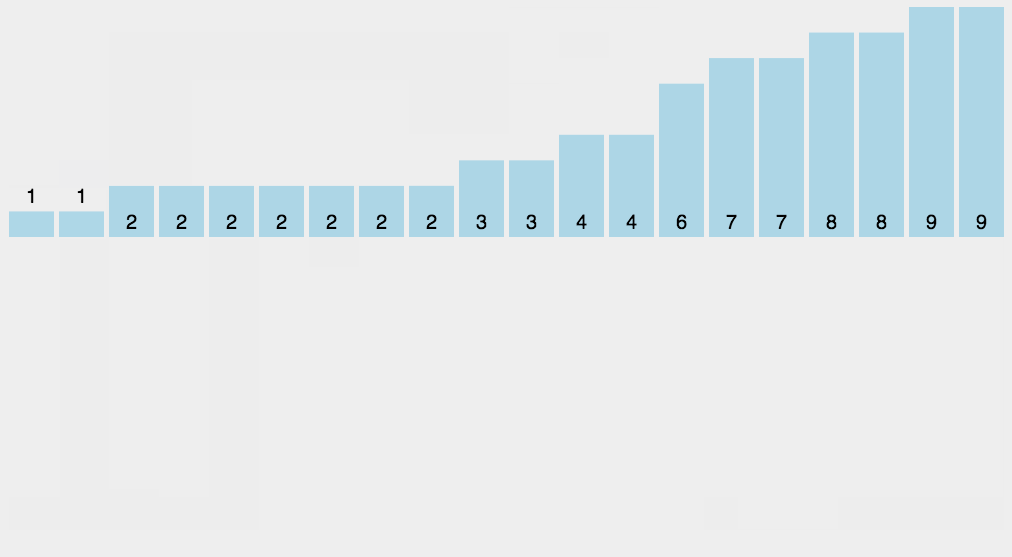
当使用计数排序时,需要注意以下几点情况:
- 计数排序适用于非负整数或者具有确定范围的元素排序。如果待排序的元素包含负数,计数排序不适用。
- 计数排序的时间复杂度为 O(n + k),其中 n 是元素个数,k 是待排序元素的最大值。当元素个数 n 较大,且最大值 k 较小时,计数排序是一个高效的排序算法。但如果 k 过大,导致计数数组非常庞大,可能会造成内存的浪费。
- 计数排序是稳定的排序算法,相同元素的相对顺序在排序后保持不变
下面是使用 Go 语言实现计数排序的代码示例:
package mainimport "fmt"func countingSort(arr []int) []int {// 找到最大值,确定计数数组的长度max := arr[0]for _, num := range arr {if num > max {max = num}}// 创建计数数组并统计元素出现次数count := make([]int, max+1)sortedArr := make([]int, len(arr))for _, num := range arr {count[num]++}// 计算累加次数for i := 1; i <= max; i++ {count[i] += count[i-1]}// 排序并构建 sortedArrfor i := len(arr) - 1; i >= 0; i-- {sortedArr[count[arr[i]]-1] = arr[i]count[arr[i]]--}return sortedArr
}func main() {arr := []int{4, 2, 2, 8, 3, 3, 1}fmt.Println("Unsorted array:", arr)arr = countingSort(arr)fmt.Println("Sorted array:", arr)
}在这个示例中,我们使用计数排序对列表 [4, 2, 2, 8, 3, 3, 1] 进行排序。根据元素范围较小(最大值为 8)且元素均为非负整数,计数排序是一个合适的选择。
总的来说,计数排序适用于非负整数或具有确定范围的元素排序,且适用于元素范围较小、均匀分布的情况。如果待排序元素范围较大或者元素分布不均匀,计数排序可能不是最优选择。在实际使用时,应根据数据的特点来选择合适的排序算法。
相关文章:
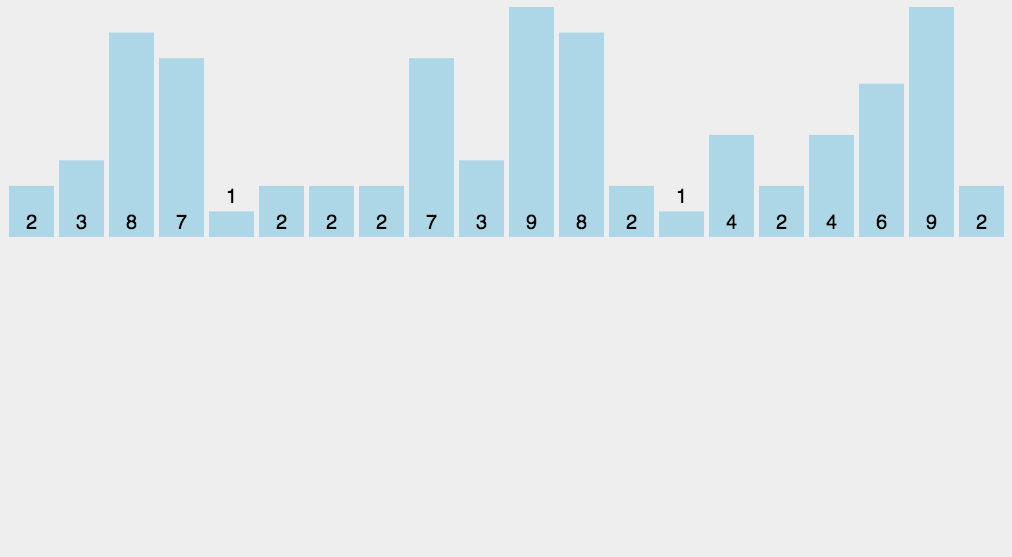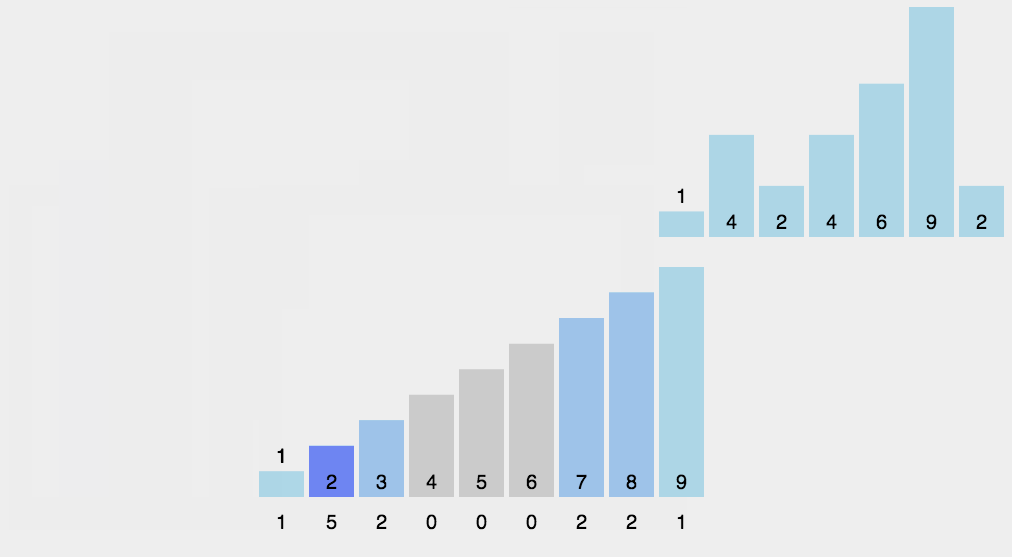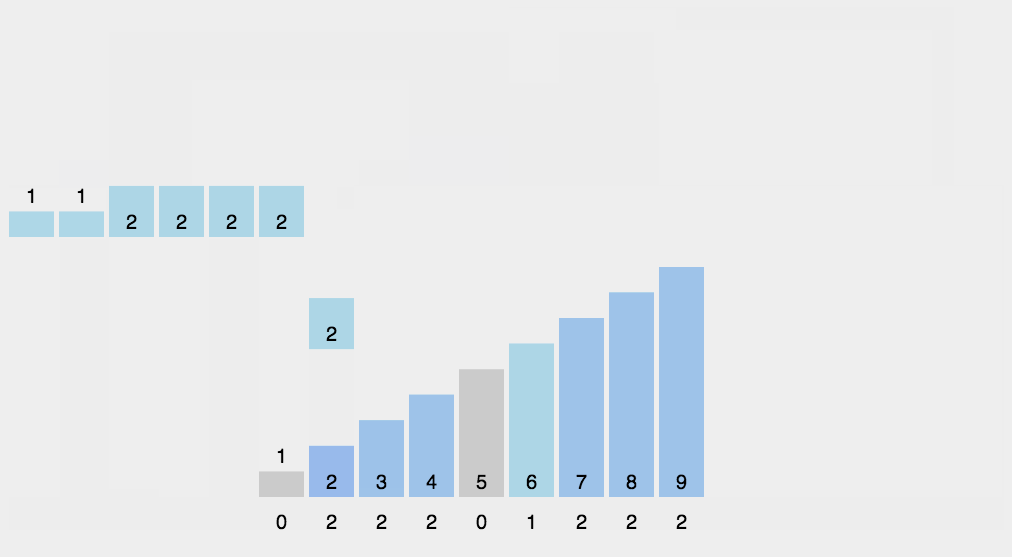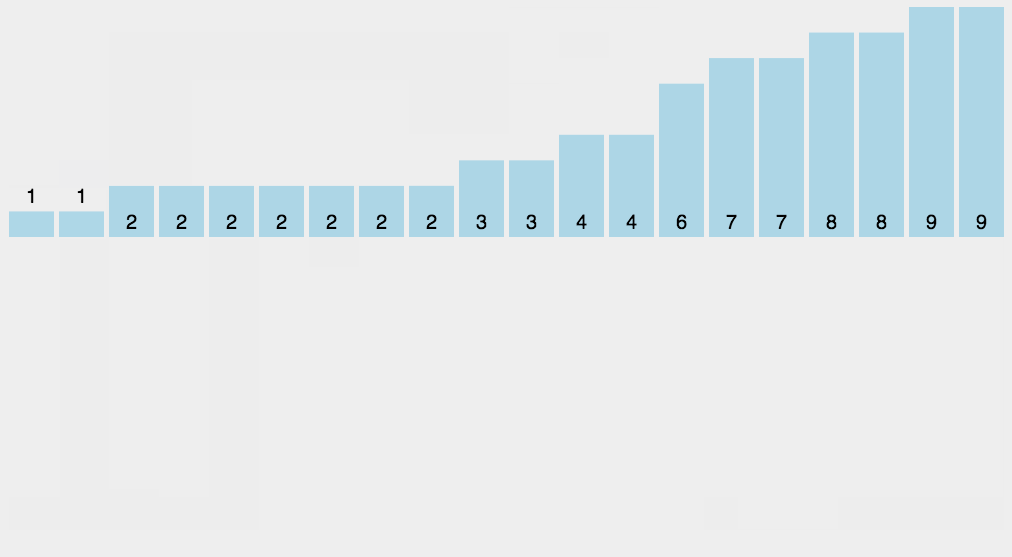
计数排序算法
计数排序 计数排序说明: 计数排序(Counting Sort)是一种非比较性的排序算法,它通过统计元素出现的次数,然后根据元素出现的次数将元素排列在正确的位置上,从而实现排序。计数排序适用于非负整数或者具有确…...

企业高性能web服务器-nginx
1.nginx简介: nginx是企业高可用的web服务器,nginx也可用来做反向代理服务器器,具有高并发,占用资源少,功能丰富,也可以作为简单的负载均衡。 nginx在企业中的功能: web服务软件 反向代理服务器…...
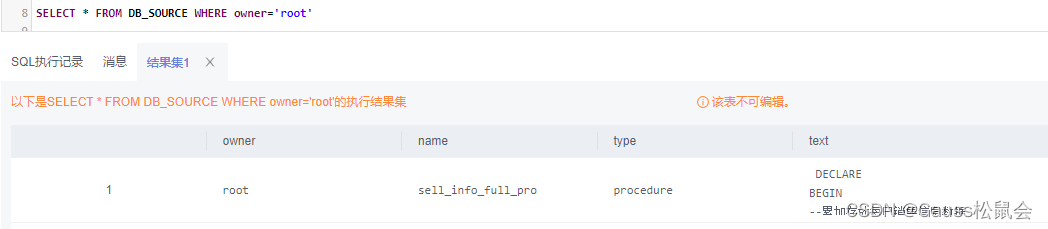
GaussDB数据库的元数据及其管理简介
目录 一、前言 二、元数据简介 1、元数据定义 2、元数据分类 3、数据库元数据管理 三、GaussDB数据库的元数据管理 1、GaussDB数据库的元数据管理 2、通过“SQL 系统表/系统视图/系统函数”的方式管理(采集)元数据 1)获取表、视图及…...

合并两个有序链表 LeetCode热题100
题目 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 思路 遍历两个链表比较大小,按从小到大添加到链表即可。 代码 /*** Definition for singly-linked list.* struct ListNode {* int val;* List…...
【C++】模拟实现string
目录 🌞专栏导读 🌛定义string类 🌛构造函数 🌛拷贝构造函数 🌛赋值函数 🌛析构函数 🌛[]操作符重载 🌛c_str、size、capacity函数 🌛比较运算符重载 &#…...

AI智慧安监视频监控汇聚平台EasyCVR调用接口出现跨域现象该如何解决?
视频监控汇聚EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有GB28181、RTSP/Onvif、RTMP等,以及厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等,能对外分发RTSP、RTMP、FLV、HLS、WebRTC等格式的视…...

无人机机巢有哪些,无人机机场/机场的主要分类
随着无人机技术的飞速发展,无人机已经渗透到了物流、农业、救援、公共安全等多个领域。而为了使这些无人机能更加高效、灵活地运行,一个新的概念应运而生,那就是无人机机巢(UAV Nest)。复亚智能无人机机巢是一种供无人…...

联想存储 HH0305_DE4000H 划分卷组、卷、主机
创建卷组 可使用卷组来创建可供主机访问的一个或多个卷。卷组是具有共同特性(如 RAID 级别和容量)的卷的容器。 关于本任务 如果拥有容量较大的驱动器且可以在控制器之间分发卷,则为每个卷组创建多个卷可以很好地利用存储容量和保护数据。…...
【Python机器学习】实验08 决策树
文章目录 决策树1 创建数据2 定义香农信息熵3 条件熵4 信息增益5 计算所有特征的信息增益,选择最优最大信息增益的特征返回6 利用ID3算法生成决策树7 利用数据构造一颗决策树Scikit-learn实例决策树分类决策树回归Scikit-learn 的决策树参数决策树调参 实验1 通过sk…...

MySQL的innoDB存储引擎如何解决幻读的问题?
MySQL的innoDB存储引擎如何解决幻读的问题 基本情况 MySQL有四种事务隔离级别,这四种隔离级别代表当存在多个事务并发冲突时,可能出现的脏读、不可重复读、幻读的问题InnoDB 在 RR 的隔离级别下 ,解决了幻读的问题幻读是指在同一个事务中&a…...

Web3.0:重新定义互联网的未来
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! Web3.0:重新定义互联网的未来 Web3.0是指下一代互联网,也称为“分布式互联网”。相比于Web1.0和Web2.0,Web3.0具有更强的去中心化、…...

2023年还能选择前端吗?
前言 在Github2022的 Octoverse年度报告上,稳居最多使用榜首的语言可以看到是JavaScript,作为前端中最为关键的一部分,这说明即使现在,前端这一块仍然是大量的人涌进来,依然是火热,但是,一门语…...
sheetJs / xlsx-js-style 纯前端实现导出 excel 表格及自定义单元格样式
文章目录 一、安装二、创建基础工作表三、设置单元格宽度/高度/隐藏单元格四、分配数字格式五、超链接六、单元格注释七、公式八、合并单元格九、自定义单元格样式十、项目地址 一、安装 xlsx 地址:https://www.npmjs.com/package/xlsxSheetJs 地址:htt…...
Redis 报错 RedisConnectionException: Unable to connect to x.x.x.x:6379
文章目录 Redis报错类型可能解决方案 Redis报错类型 org.springframework.data.redis.connection. spingboot调用redis出错 PoolException: Could not get a resource from the pool; 连接池异常:无法从池中获取资源; nested exception is io.lettuce.core. 嵌套异常 RedisConn…...

Stable Diffusion - 真人照片的高清修复 (StableSR + GFPGAN) 最佳实践
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/132032216 GFPGAN (Generative Facial Prior GAN) 算法,用于实现真实世界的盲脸恢复的算法,利用预训练的面部 GAN…...
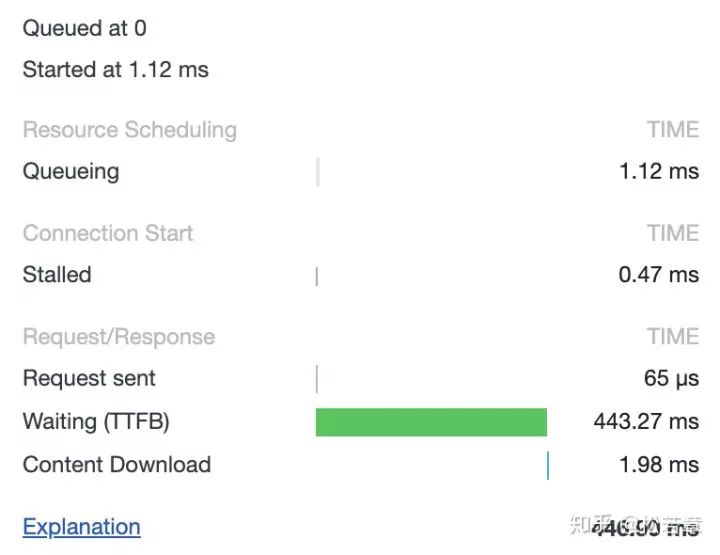
细讲一个 TCP 连接能发多少个 HTTP 请求(一)
一道经典的面试题是从 URL 在浏览器被被输入到页面展现的过程中发生了什么,大多数回答都是说请求响应之后 DOM 怎么被构建,被绘制出来。但是你有没有想过,收到的 HTML 如果包含几十个图片标签,这些图片是以什么方式、什么顺序、建…...

了解 CVSS:通用漏洞评分系统的应用
漏洞威胁管理至关重要,因为网络犯罪是一种持续存在的全球风险。网络犯罪分子愿意利用软件中的任何漏洞来访问网络和设备。对使用该软件的软件开发人员和组织的影响可能很严重。用户必须处理攻击的结果,例如赎金或数据盗窃,并且还可能面临法律…...
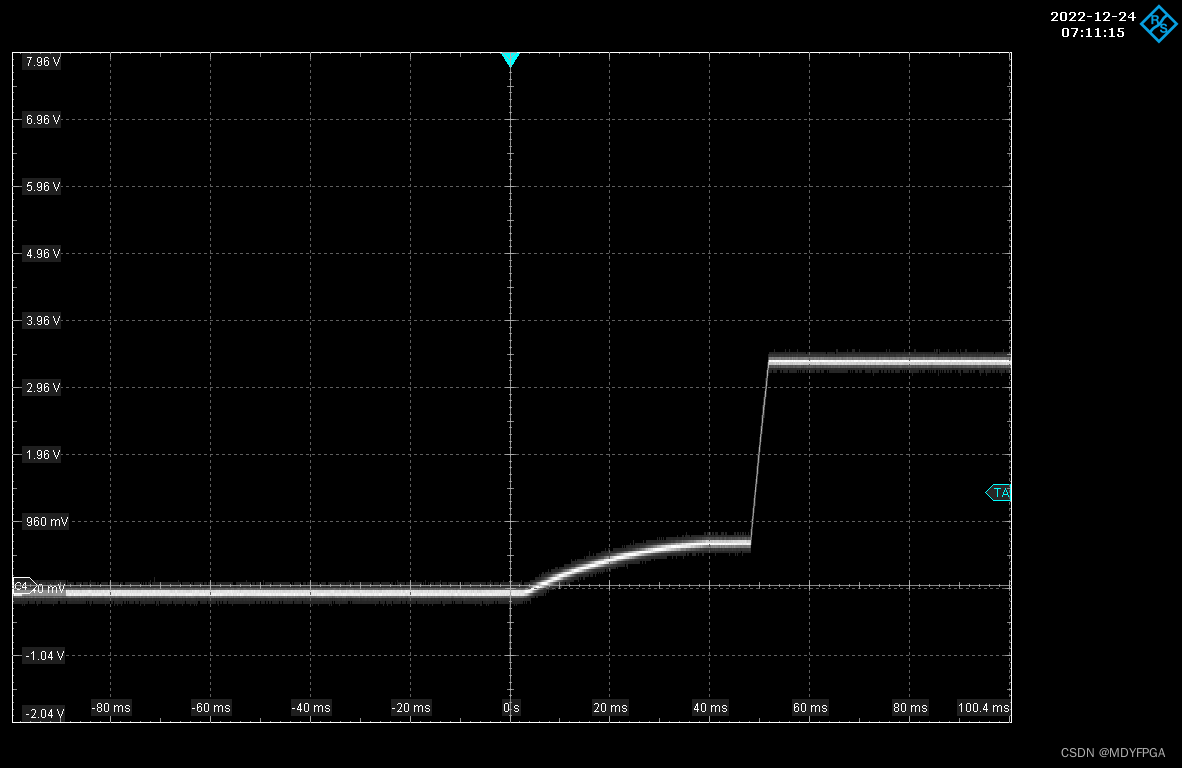
Xilinx FPGA电源设计与注意事项
1 引言 随着半导体和芯片技术的飞速发展,现在的FPGA集成了越来越多的可配置逻辑资源、各种各样的外部总线接口以及丰富的内部RAM资源,使其在国防、医疗、消费电子等领域得到了越来越广泛的应用。当采用FPGA进行设计电路时,大多数FPGA对上电的…...
前端:地图篇(一)
1、前言 在很多的出行程序中,都会使用到地图这一个功能,在实际的开发中我们也不会去开发一个自己的地图模型。如果自己开发一个地图模型,那么需要投入的成本、人力都是非常巨大的。所以我们很多网站和APP中使用的都是第三方的接口和JS&#…...
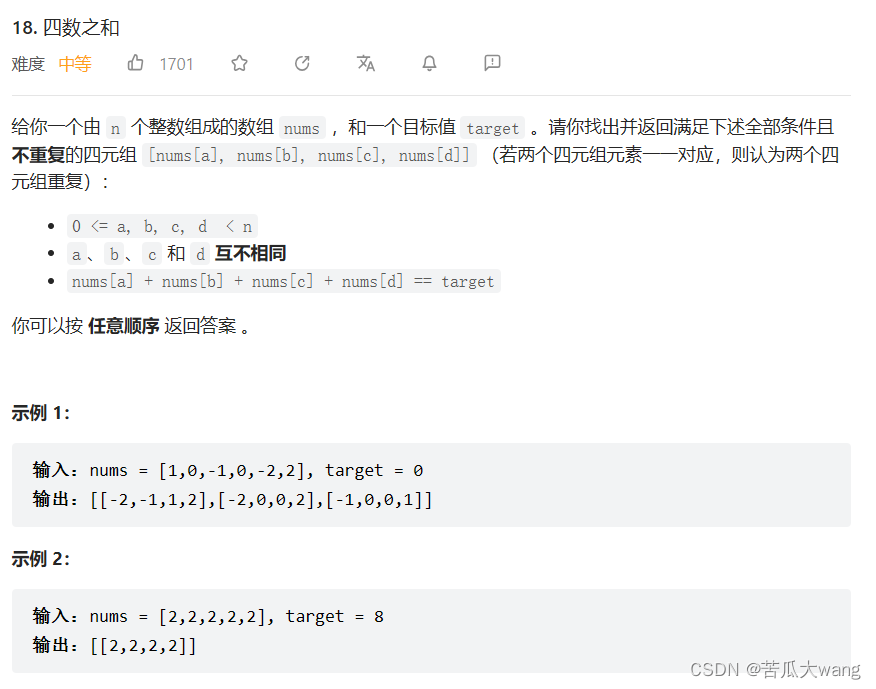
刷题笔记 day6
力扣 57 和为s的两个整数 class Solution { public:vector<int> twoSum(vector<int>& nums, int target) {vector<int> v;int i 0 , j nums.size()-1;while(i < j){if(nums[i] nums[j] > target){--j;}else if(nums[i] nums[j] < target){i…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
