2022牛客寒假算法基础集训营1
B题 炸鸡块君与FIFA22
题目大意:
给出胜负序列,每次询问区间 (l,r,s) ,回答在经历 (l-r) 之后积分是多少,初始积分为 (s)
胜 (+1) 积分,平 (+0) 积分,败的时候如果此时积分为 (3) 的倍数则 (-0) ,否则 (-1)
思路解析:
(ST) 表,预处理出 (st[k][i][j]) 表示表示在初始分数为k的情况下经历了 ([i,i+2^j-1]) 一段后分数的变化量
查询倍增查询即可
AC代码:
#include<bits/stdc++.h>
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#pragma GCC optimize(2)
#pragma GCC optimize(3,“Ofast”,“inline”)
#define endl ‘\n’
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int maxn=1e6+5;
int n,q;
char a[maxn];
int st[3][maxn][20],lg[maxn];
void init(){
lg[1]=0;lg[2]=1;
for(int i=3;i<=n;i++)lg[i]=lg[i/2]+1;for(int j=0;j<20;j++){for(int i=1;i+(1<<j)-1<=n;i++){if(!j){if(a[i]=='W')st[0][i][j]=st[1][i][j]=st[2][i][j]=1;if(a[i]=='L')st[0][i][j]=0,st[1][i][j]=st[2][i][j]=-1;if(a[i]=='D')st[0][i][j]=st[1][i][j]=st[2][i][j]=0;}else {int p=i+(1<<(j-1));st[0][i][j]=st[0][i][j-1]+st[(0+st[0][i][j-1]+3)%3][p][j-1];st[1][i][j]=st[1][i][j-1]+st[(1+st[1][i][j-1]+3)%3][p][j-1];st[2][i][j]=st[2][i][j-1]+st[(2+st[2][i][j-1]+3)%3][p][j-1];}}
}
}
int query(int s,int l,int r){
int pos=l;
while(pos<=r){int j=0;while(pos+(1<<j)-1<=r)j++;j--;s+=st[s%3][pos][j];pos+=(1<<j);
}
return s;
}
int main(){
IOScin>>n>>q;cin>>a+1;init();while(q--){int l,r,s;cin>>l>>r>>s;cout<<query(s,l,r)<<endl;
}
}
C题 Baby’s first attempt on CPU
题目大意:
给出 (n) 个句子和每个句子与前三句的关系,如果两句之间有关系的话,那么你必须在他们添加空语句使得有关系的两句话中间至少隔了三句话,问最少需要插入多少空语句使得所有语句合法
思路解析:
模拟,在另一个数组中插入,如果有关系的语句就从后往前看隔了几个,需要插入几个,计算即可
AC代码:
#include<bits/stdc++.h>
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#pragma GCC optimize(2)
#pragma GCC optimize(3,“Ofast”,“inline”)
#define endl ‘\n’
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int maxn=505;
int n;
int a[maxn][maxn];
int b[maxn*10],top;
int main(){
IOScin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=3;j++){cin>>a[i][j];if(a[i][j]){int now=i-j,sum=0;for(int k=top;k>0;k--){if(b[k]==now)break;sum++;}if(sum<3){for(int k=1;k<=3-sum;k++)b[++top]=0;}}}b[++top]=i;
}
cout<<top-n<<endl;
}
D题 牛牛做数论
题目大意&思路解析:
首先我们要知道取得最大值和最小值实质是让我们求什么:
第一个是让我们计算素数序列的前缀积不超过 (n) 的最大值
第二个是让我们求 ([2,n]) 中最大的质数
前缀积不需要很多素数,因为一小部分的前缀积就已经很大了,超过了 (1e9)
试除法判断素数即可求最大
AC代码:
#include<bits/stdc++.h>
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#pragma GCC optimize(2)
#pragma GCC optimize(3,“Ofast”,“inline”)
#define endl ‘\n’
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int maxn=1e6+5;
bool pd(int x){
for(int i=2;i<=x/i;i++){
if(x%i==0)return false;
}
return true;
}
ll prime[maxn],st[maxn],tot;
ll sum[maxn];
void get_primes(int n){
for(int i=2;i<=n;i++){
if(!st[i])prime[++tot]=i;
for(int j=1;prime[j]<=n/i;j++){
st[prime[j]*i]=1;
if(i%prime[j]==0)break;
}
}
}
int main(){
IOSint t;
cin>>t;get_primes(100);sum[0]=1;
for(int i=1;i<=100;i++)sum[i]=sum[i-1]*prime[i];while(t--){int n;cin>>n;if(n==1){cout<<-1<<endl;continue;}for(int i=1;i<=n;i++){if(sum[i+1]>n){cout<<sum[i]<<" ";break;}}while(!pd(n))n--;cout<<n<<endl;
}
}
E题 炸鸡块君的高中回忆
题目大意:
有 (n) 个人 (m) 张卡,每一次进去 (m) 个然后回来一个带回 (m) 张卡,重复操作,进来和出去都需要一个单位时间,问最短时间,若无解,输出 (-1)
思路解析:
无解情况:只有一张卡并且总人数大于 (1)
特殊情况:卡的数量大于等于人数,答案为 (1)
一般情况:模拟即可(相当于除了第一次每一次可以带走 (m-1) 个人)
AC代码:
#include<bits/stdc++.h>
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#pragma GCC optimize(2)
#pragma GCC optimize(3,“Ofast”,“inline”)
#define endl ‘\n’
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int maxn=1e6+5;
int main(){
IOSint t;
cin>>t;while(t--){ll n,m,ans=0;cin>>n>>m;if(m>=n)cout<<1<<endl;else if(m==1)cout<<-1<<endl;else {n-=m;ans++;ans+=n/(m-1)*2;if(n%(m-1))ans+=2;cout<<ans<<endl;}
}
}
F题 中位数切分
题目大意:
给出序列 (a[]) ,和一个正整数 (m) ,问最多可以把序列分成几段,使得每一段的中位数都大于等于 (m) ,(偶数个数的中位数是中间较小的那一个),若无解,输出 (-1)
思路解析:
我们考虑一个合法序列的中位数满足什么条件:序列中大于等于 (m) 的数量大于小于 (m) 的数量。
所以我们可以贪心的去选择:
从前往后枚举,如果当前位置的左边合法并且右边的序列是可分割的,那么就把这一段分割出去
用后缀维护区间大于等于 (m) 的数量即可
AC代码:
#include<bits/stdc++.h>
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#pragma GCC optimize(2)
#pragma GCC optimize(3,“Ofast”,“inline”)
#define endl ‘\n’
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int maxn=1e6+5;
int n,m;
int a[maxn];
int up[maxn],dn[maxn];
int main(){
IOSint t;
cin>>t;while(t--){cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];up[i]=0;dn[i]=0;}for(int i=1;i<=n+50;i++){up[i]=0;dn[i]=0;}for(int i=n;i>=1;i--){up[i]=up[i+1];dn[i]=dn[i+1];if(a[i]>=m)up[i]++;else dn[i]++;}ll ans=0;int l=1;for(int i=1;i<=n;i++){if(i==n){if(up[l]>dn[l])ans++;break;}if((up[l]-up[i+1]>dn[l]-dn[i+1])&&up[i+1]>dn[i+1]){ans++;l=i+1;}}if(ans==0)cout<<"-1"<<endl;else cout<<ans<<endl;
}
}
G题 ACM is all you need
题目大意:
给出序列 (f[]) ,你可以选择一个数 (b) ,使每个 (f_i=|f_i-b|+b) ,问有多少个 (local minimum)
(local minimum) 定义:(f_i<min(f_i-1,f_i+1))
思路解析:
首先 (+b) 是没有用的,可以直接去掉
然后,对与绝对值,我们可以看作是 (f_i) 与 (b) 的距离,对于 (2<=i<=n-1) 的 (f) 来说,我们可以计算出当前数变化后不满足条件是 (b) 的取值范围,可以得到一个 (b) 的区间,那么我们就会得到若干 (b) 的区间,每一个区间代表着使得某一个 (f) 不成立
这样问题就转化为了在数轴上区间覆盖问题,(map) 维护差分即可
AC代码:
#include<bits/stdc++.h>
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#pragma GCC optimize(2)
#pragma GCC optimize(3,“Ofast”,“inline”)
#define endl ‘\n’
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int maxn=1e6+5;
const int inf=1e9+7;
int n;
int a[maxn];
map<int,int>q;
int main(){
IOSint t;
cin>>t;while(t--){q.clear();cin>>n;for(int i=1;i<=n;i++)cin>>a[i];int tot=0;for(int i=2;i<n;i++){if(a[i]==a[i-1]||a[i]==a[i+1])continue;tot++;if(a[i]<a[i-1]&&a[i]<a[i+1]){int x=min(a[i-1],a[i+1]);q[-1]++;q[(x+a[i]-1)/2+1]--;}else if(a[i]>a[i+1]&&a[i]>a[i-1]){int x=max(a[i-1],a[i+1]);q[(x+a[i])/2+1]++;}else{int x=max(a[i-1],a[i+1]);q[(x+a[i]-1)/2+1]--;int r=(x+a[i]-1)/2;x=min(a[i-1],a[i+1]);q[(x+a[i])/2+1]++;}}ll now=0,ans=q[-1];for(auto &i:q){now+=i.second;ans=min(ans,now);}cout<<ans<<endl;
}
}
H题 牛牛看云
题目大意:
给出序列 (a[]) ,求(\sum_{i=1}n\sum_{j=i}n|a_i+a_j-1000|)
思路解析:
我们可以在值域上枚举,我们会发现每一个数都会和其他任何一个数计算一次(包括自己),所以我们只需要在值域上枚举计算即可,注意我们枚举计算的时候会多计算一次自己与自己的计算结果,单独计算即可
AC代码:
#include<bits/stdc++.h>
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#pragma GCC optimize(2)
#pragma GCC optimize(3,“Ofast”,“inline”)
#define endl ‘\n’
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int maxn=1e6+5;
int n;
ll a[maxn];
ll sum[maxn];
int main(){
IOScin>>n;for(int i=1;i<=n;i++){cin>>a[i];sum[a[i]]++;
}
ll ans=0;
for(int i=0;i<=1000;i++){if(sum[i]==0)continue;ll tot=0;for(int j=0;j<=1000;j++){ans+=sum[i]*sum[j]*abs(i+j-1000);}ans+=sum[i]*abs(i+i-1000);
}
cout<<ans/2<<endl;
}
I题 B站与各唱各的
题目大意:
(n) 个人 (m) 句歌词,每个人每一句都可以选择唱或者不唱,如果有一句歌词数所有人都唱了或者都没唱,那么就失败了,否则成功,问期望成功句子的数量
思路解析:
我们可以发现 (m) 句歌词是独立的,所以可以计算每一句成功的期望然后乘以 (m)
可得出结论:(ans=m*\frac{2n-2}{2n})
AC代码:
#include<bits/stdc++.h>
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#pragma GCC optimize(2)
#pragma GCC optimize(3,“Ofast”,“inline”)
#define endl ‘\n’
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int maxn=1e6+5;
const int mod=1e9+7;
ll ksm(ll a, ll b)
{
ll ans=1,base=a%mod;
while(b)
{
if(b&1)
ans=ansbase%mod;
base=basebase%mod;
b>>=1;
}
return ans;
}
ll inv(ll x){
return ksm(x,mod-2)%mod;
}
int main(){
IOSint t;
cin>>t;while(t--){ll n,m;cin>>n>>m;if(n==1){cout<<0<<endl;continue;}ll p=ksm(2,n)%mod;cout<<m*(p+mod-2)%mod*inv(p)%mod<<endl;
}
}
J题 小朋友做游戏
题目大意:
给出 (A) 个安静小朋友, (B) 个调皮小朋友,每个人有一个权值,选出 (n) 个人围成一个圈并且满足没有两个调皮小朋友是挨着的,问最大权值和。如果没有任何方案可行,输出 (-1)
思路解析:
首先我们判断无解情况:
在 (n) 个人中,必须选出 ((n+1)/2) 个小朋友来把调皮隔开,所以安静小朋友必须大于等于 ((n+1)/2)
然后我们先从安静小朋友里选择最大的 ((n+1)/2) 个,剩下的和调皮小朋友一起排序,从大到小贪心去选,直到凑成 (n) 个人
AC代码:
#include<bits/stdc++.h>
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#pragma GCC optimize(2)
#pragma GCC optimize(3,“Ofast”,“inline”)
#define endl ‘\n’
#define pii pair<int,int>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int maxn=1e6+5;
vectora;
ll b[maxn],q[maxn];
int main(){
IOSint t;
cin>>t;while(t--){int x,y,n;cin>>x>>y>>n;a.clear();for(int i=1;i<=x;i++)cin>>b[i];for(int i=1;i<=y;i++)cin>>q[i];if(x<(n+1)/2){cout<<-1<<endl;continue;}sort(b+1,b+x+1);ll ans=0;for(int i=x-(n+1)/2+1;i<=x;i++){ans+=b[i];}for(int i=1;i<=x-(n+1)/2;i++){a.push_back({b[i],1});}for(int i=1;i<=y;i++){a.push_back({q[i],0});}sort(a.begin(),a.end());int tot=n-(n+1)/2;int sum=(n+1)/2;for(int i=a.size()-1;i>=0;i--){if(sum==n)break;if(tot&&a[i].second==0){ans+=a[i].first;tot--;}else {ans+=a[i].first;}sum++;}cout<<ans<<endl;
}
}
相关文章:

2022牛客寒假算法基础集训营1
B题 炸鸡块君与FIFA22 题目大意: 给出胜负序列,每次询问区间 (l,r,s) ,回答在经历 (l-r) 之后积分是多少,初始积分为 (s) 胜 (1) 积分,平 (0) 积分,败的时候如果此时积分为 (3) 的倍数则 (-0) ,…...

API对接:构建连接不同系统的技术桥梁
API(Application Programming Interface)是一种用于不同软件系统之间进行通信和数据交换的技术。本文将介绍API对接的基本概念和原理,并通过代码示例演示如何使用API对接不同系统,解决数据传输与通信的难题。 在当今数字化时代&a…...
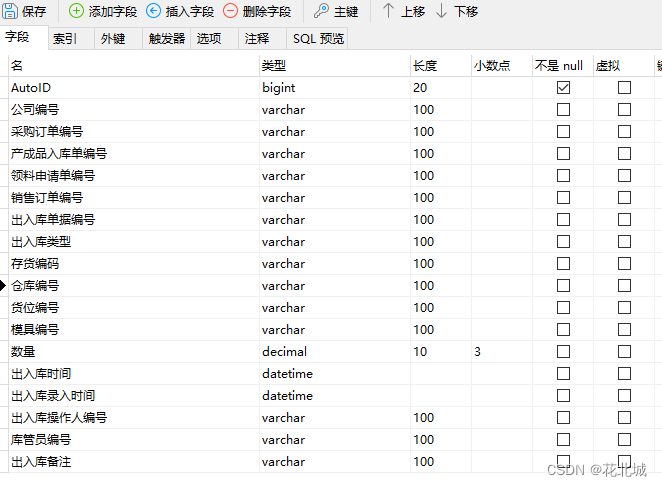
【MySQL】仓储--维护出入库流水、库存,去重数量逻辑修正
系列文章 C#底层库–MySQLBuilder脚本构建类(select、insert、update、in、带条件的SQL自动生成) 本文链接:https://blog.csdn.net/youcheng_ge/article/details/129179216 C#底层库–MySQL数据库操作辅助类(推荐阅读࿰…...

用Log4j 2记录日志
说明 maven工程中增加对Log4j 2的依赖 下面代码示例的maven工程中的pom.xml文件中需要增加对Log4j 2的依赖: <dependency><groupId>org.apache.logging.log4j</groupId><artifactId>log4j-core</artifactId><version>2.20.0&…...

【Java面试】Paxos和Raft协议的区别?
面试官:你简历上说了解Paxos和Raft协议,说一下你对这两个协议的了解? 我:Paxos算法和Raft算法都是用于实现分布式系统中的一致性的算法,确保不同节点之间的数据一致。 我:Paxos算法它的目标是使多个节点能…...

手机浏览器H5打开微信小程序支付,自定义传参
微信官方提供的开放文档如下: 静态网站 H5 跳小程序 | 微信开放文档 想必大家都能看懂官网提供的文档,但实战时却遇到很多问题,博主总结一下遇到的坑,如果您也有遇到,希望可以帮到您。 1.小程序已经发布上线了&…...
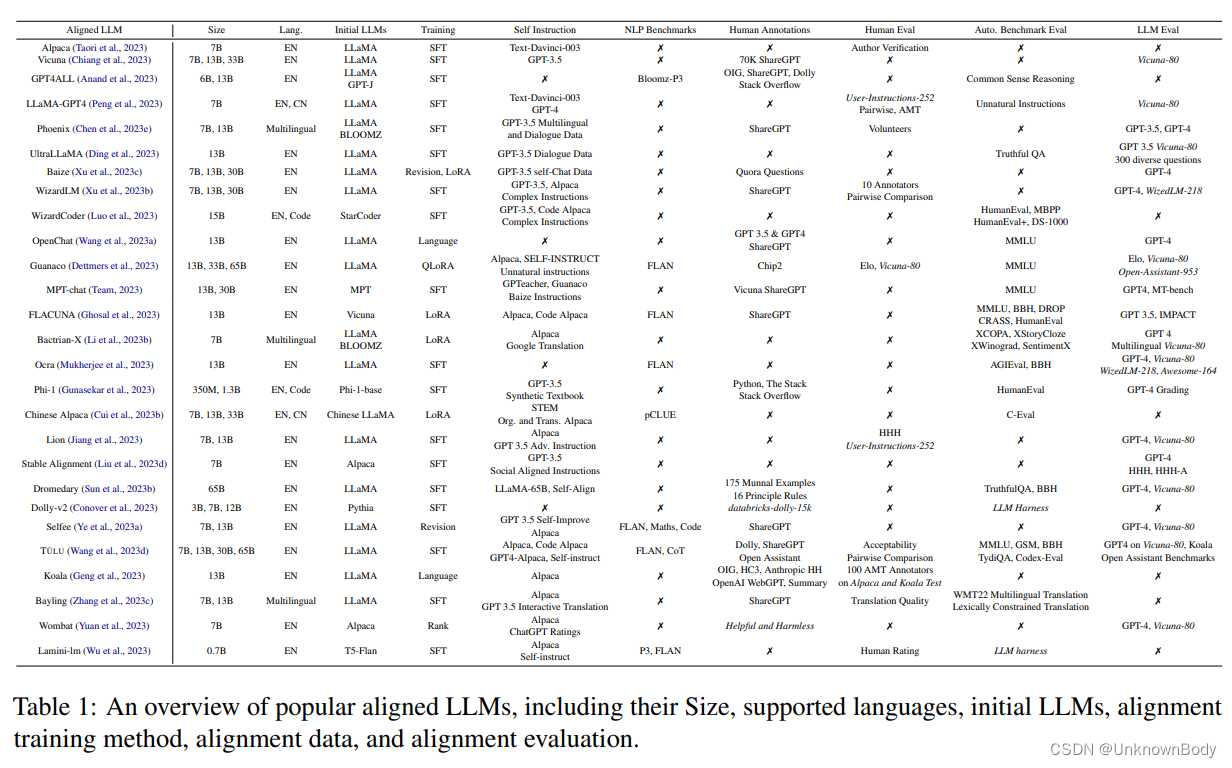
Aligning Large Language Models with Human: A Survey
本文也是LLM相关的综述文章,针对《Aligning Large Language Models with Human: A Survey》的翻译。 对齐人类与大语言模型:综述 摘要1 引言2 对齐数据收集2.1 来自人类的指令2.1.1 NLP基准2.1.2 人工构造指令 2.2 来自强大LLM的指令2.2.1 自指令2.2.2 …...
windows图标白了,刷新图标
1.进入C盘,user(用户文件夹),进入当前用户文件夹,再进入隐藏文件夹(AppDada),最后进入Local 2.删除Local文件夹里的IconCache.db文件 3.重启资源管理器 -------------------------------------------- 或者创建bat文件…...
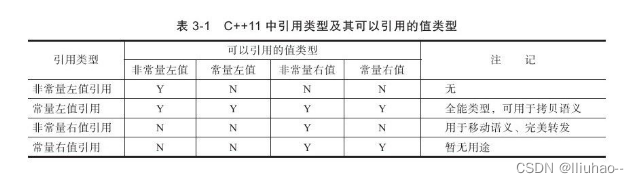
C++ 左值和右值
C 左值和右值 左值、右值左值引用、右值引用std::move()std::move()的实现引用折叠 完美转发forward()的实现函数返回值是左值还是右值如何判断一个值是左值还是右值 左值、右值 在C11中所有的值必属于左值、右值两者之一,右值又可以细分为纯右值、将亡值。在C11中…...

c++学习(智能指针)[29]
RALL RALL(Resource Acquisition Is Initialization)是一种 C 的编程技术,用于管理资源的获取和释放。它的基本思想是在对象的构造函数中获取资源,在对象的析构函数中释放资源,从而确保资源的正确获取和释放。 RALL 的…...
B站高播放又涨粉的带货UP主怎么做?
飞瓜数据(B站版)上线新功能【带货达人榜】,由榜单显示,B站7月带货达人中,平均播放量最高的是UP主下个月一定中100万。 带货视频仅1支,播放量已经高达679万,值得一提的是,6月他也是带…...
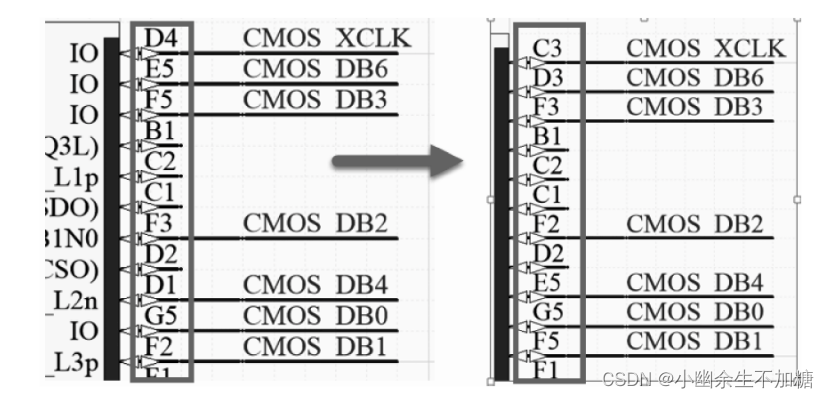
AD21 PCB设计的高级应用(四)FPGA的管脚交换功能
(四)FPGA的管脚交换功能 高速 PCB 设计过程中,涉及的 FPGA等可编程器件管脚繁多,也因此导致布线的烦琐与困难,Altium Designer 可实现 PCB 中 FPGA 的管脚交换,方便走线。 1.FPGA管脚交换的要求 (1)一般情况下,相同电压的 Bank之…...

超低功耗LCD段码屏驱动显示芯片VK1621原厂芯片
型 号:VK1621 / 品 牌:VINKA/永嘉微电 最新年份 VK1621 是一个324的LCD驱动器,可软体程式控制使其适用于多样化的LCD应用线路,仅用到3至4条信号线便可控制LCD驱动器,除此之外也可介由指令使其進入省电模式 M1855 …...

【深入探索Docker】:开启容器化时代的技术奇迹
深入探索Docker 深入探索Docker:开启容器化时代的技术奇迹前言1. 容器化:实现快速部署和可移植性2. 虚拟化:提高安全性和可靠性3. 映像:打包应用及依赖项的模板4. 网络管理:连接容器和主机5. 持久化数据:保…...

【Ajax】笔记-JQuery发送jsonp请求
前端 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>jQuery-jsonp</title><style>#re…...

docker更换数据存储路径
1. 先停掉docker服务 sudo systemctl stop docker 可能会出现的问题: 这样会导致docker关闭失败,解决办法:systemctl stop docker.socket 确保docker关闭: 2.备份现在的 Docker 数据存储目录 /var/lib/docker(默认路径) mv /var/lib/docker /var/lib/…...

GPT告诉你如何延长周末体验
对于常常感到疲劳的打工人和学生党,过周末需要找到一种平衡,既能够休息放松,又能够提升身心能量。以下是一些建议,希望对你有所帮助: 制定休息计划:在周末前,制定一个休息计划,明确…...
一百四十一、Kettle——kettle8.2在Windows本地开启carte服务以及配置子服务器
一、目的 在kettle建好共享资源库后,为了给在服务器上部署kettle的carte服务躺雷,先在Windows本地测试一下怎么玩carte服务 二、Kettle版本以及在Windows本地安装路径 kettle版本是8.2 pdi-ce-8.2.0.0-342 kettle本地安装路径是D:\j…...

你知道充电桩控制主板的结构吗?
你知道充电桩控制主板的结构吗? 你是否曾经遇到过电动车行驶途中突然没电的情况?不用担心,解决这个问题的方法之一就是使用充电桩。那么,控制主板是如何控制充电桩的呢?让我们一起来探究一下。 充电桩控制主板由多种元件组成,包括主控芯片…...
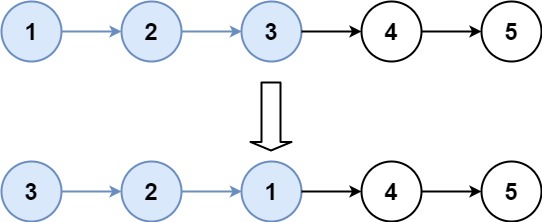
LeetCode 25题:K个一组翻转链表
题目: 给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。 k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。 你不能只是单纯…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
