【学会动态规划】最佳买卖股票时机含冷冻期(15)
目录
动态规划怎么学?
1. 题目解析
2. 算法原理
1. 状态表示
2. 状态转移方程
3. 初始化
4. 填表顺序
5. 返回值
3. 代码编写
写在最后:
动态规划怎么学?
学习一个算法没有捷径,更何况是学习动态规划,
跟我一起刷动态规划算法题,一起学会动态规划!
1. 题目解析
题目链接:309. 最佳买卖股票时机含冷冻期 - 力扣(Leetcode)
这道题很好理解,其实就是买股票的时候多了一个冷冻期。
2. 算法原理
1. 状态表示
因为他有三种情况,所以我们也有三种状态表示:
dp[ i ][ 0 ] 表示第 i 天是 “买入” 状态,此时的最大利润。
dp[ i ][ 1 ] 表示第 i 天是 “可卖出” 状态,此时的最大利润。
dp[ i ][ 2 ] 表示第 i 天是 “冷冻” 状态,此时的最大利润。
2. 状态转移方程
我们一个一个分析状态表示:
首先是买入状态,怎么样让第 i 天进入买入状态?
如果 i - 1 天结束是买入状态(买过股票)那就已经是买入状态,
如果 i - 1 天结束是可交易状态(可以卖股票但没买)那只要这天买入,就可以进入买入状态,
如果 i - 1 天结束是冷冻状态(就是卖出的后一天)这样就不能进入买入状态。
然后是冷冻状态,怎么样让第 i 天进入冷冻状态?
如果 i - 1 天结束是买入状态,那只要这天卖出,就能进入冷冻状态,
如果 i - 1 天结束是可交易状态,那只要这天卖了,也能进入冷冻状态,
如果 i - 1 天结束是冷冻状态,那第 i 天结束不可能是冷冻状态,因为没东西可以卖了。
然后是可交易状态,怎么样让第 i 天进入可交易状态?
如果 i - 1 天结束是买入状态,那就不是可交易状态,而是买入状态。
如果 i - 1 天结束是可交易状态,那也只需要啥都不干就是可交易状态,
如果 i - 1 天结束是冷冻状态,那也只需要啥都不干就是可交易状态。
所以我们根据上面的分析来写状态转移方程:
dp[ i ][ 0 ] = max( dp[ i - 1 ][ 0 ],dp[ i - 1 ][ 1 ] - p[ i ] )
dp[ i ][ 1 ] = max( dp[ i - 1 ][ 1 ],dp[ i - 1 ][ 2 ] )
dp[ i ][ 2 ] = dp[ i - 1 ][ 0 ] + p[ i ]
3. 初始化
我们只需要把 dp[ 0 ][ 0 ] 初始化成 -p[ 0 ] 即可,因为买入了所以最大利润就是一个负值。
4. 填表顺序
从左往右,依次填写三个表即可。
5. 返回值
其实就是:max( dp[ n - 1 ][ 1 ],dp[ n - 1 ][ 2 ] )
第一种买入的情况不考虑,因为都买入了,肯定不会是最大利润。
3. 代码编写
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(3));dp[0][0] = -prices[0];for(int i = 1; i < n; i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);dp[i][2] = dp[i - 1][0] + prices[i];}return max(dp[n - 1][1], dp[n - 1][2]);}
};写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果感到有所收获的话可以给博主点一个赞哦。
如果文章内容有遗漏或者错误的地方欢迎私信博主或者在评论区指出~
相关文章:

【学会动态规划】最佳买卖股票时机含冷冻期(15)
目录 动态规划怎么学? 1. 题目解析 2. 算法原理 1. 状态表示 2. 状态转移方程 3. 初始化 4. 填表顺序 5. 返回值 3. 代码编写 写在最后: 动态规划怎么学? 学习一个算法没有捷径,更何况是学习动态规划, 跟我…...

随机RSI震荡指标公式(StochRSI),RSI和KDJ二合一
随机RSI震荡指标(StochRSI)是由图莎尔钱德和斯坦利克罗发明的一种摆动指标,结合了相对强弱指标(RSI)和随机指标(KDJ)的原理,目的是提高灵敏度,解决RSI难以达到超买超卖区的问题,以便…...
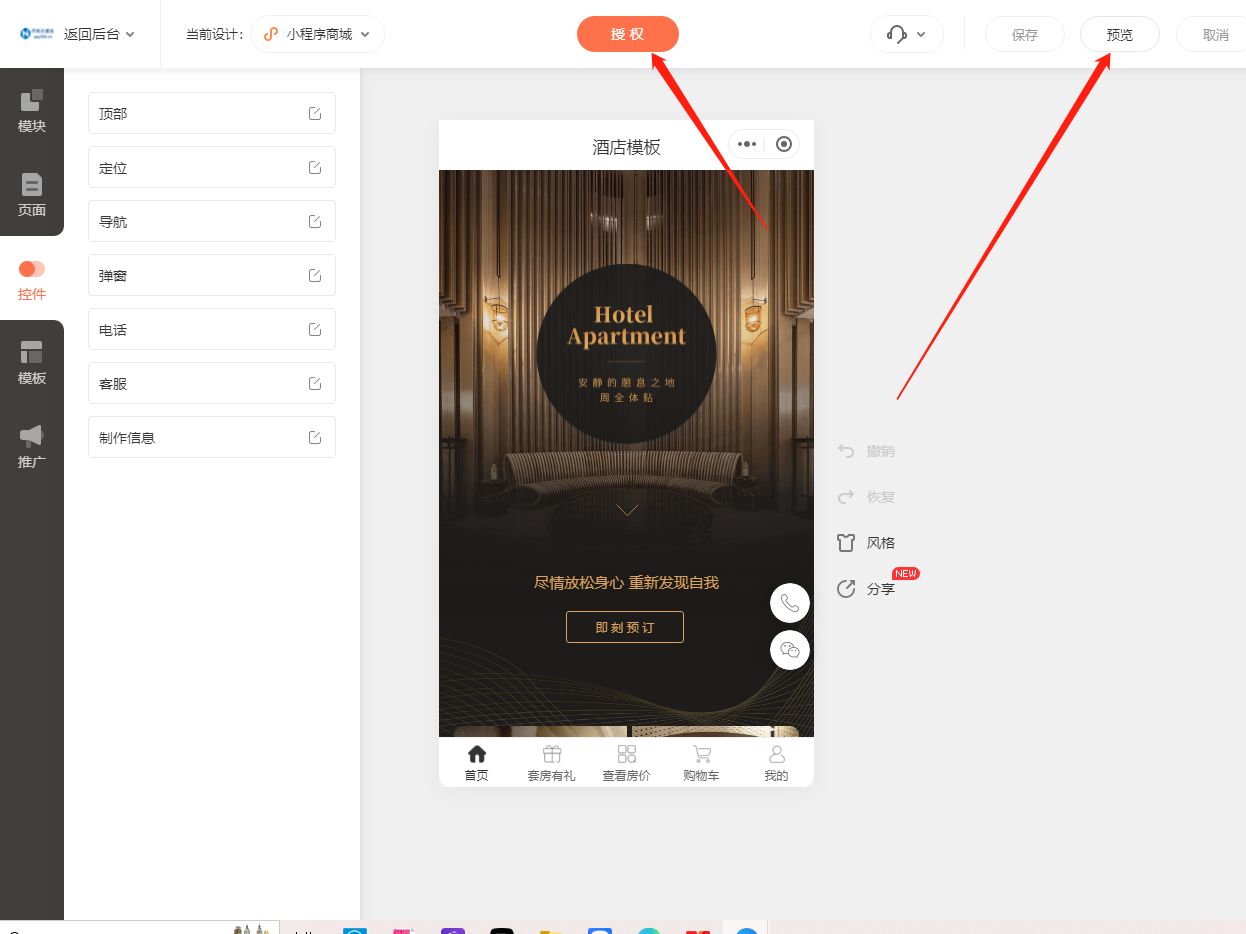
轻松搭建酒店小程序
酒店小程序的制作并不需要编程经验,只需要按照以下步骤进行操作,就能很快地搭建自己的小程序商城。 第一步,注册登录账号进入操作后台,找到并点击【商城】中的【去管理】进入商城的后台管理页面,然后再点击【小程序商城…...
算法通过村——Hash和队列问题解析
算法的备胎Hash和找靠山的队列 备胎Hash Hash,不管是算法,还是在工程中都会大量使用。很多复杂的算法问题都用Hash能够轻松解决,也正是如此,在算法例就显得没什么思维含量,所以Hash是应用里的扛把子,但在算…...
租赁类小程序定制开发|租赁管理系统源码|免押租赁系统开发
随着互联网的发展,小程序成为了一种重要的移动应用开发方式。租赁小程序作为其中的一种类型,可以为很多行业提供便利和创新。下面我们将介绍一些适合开发租赁小程序的行业。 房屋租赁行业:租房小程序可以帮助房东和租户快速找到合适的租赁…...

后端进阶之路——浅谈Spring Security用户、角色、权限和访问规则(三)
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 「推荐专栏」: ★java一站式服务 ★ ★前端炫酷代码分享 ★ ★ uniapp-从构建到提升★ ★ 从0到英雄,vue成神之路★ ★ 解决算法,一个专栏就够了★ ★ 架…...

Mac 安装不在 Apple 商店授权的应用程序
文章目录 一、场景介绍二、实操说明 一、场景介绍 在日常的工作生活中,发现一些好用的应用程序,但是出于某些原因,应用程序的开发者并没有将安装包上架到苹果商店。 那么这些优秀的应用程序下载安装以后就会出现如下弹框被拒之门外 二、实操…...

【MyBatis】MyBatis把空字符串转换成0的问题处理方案(96)
先看问题: Postman入参: MyBatis采用map循环插入: // Mapper接口层void addPar(Param(value "question") Map<String, Object> paramMap);<!-- 新增:参数 --><insert id"addPar" parameterType"map">INSERT IGNO…...

OpenLayers实战,OpenLayers获取移动端精确定位,OpenLayers适配App混合H5方式调用手机定位位置并定位到指定点
专栏目录: OpenLayers实战进阶专栏目录 前言 本章讲解OpenLayers如何获取移动端精确定位位置。不使用任何native本地方法,只使用纯js实现。 本篇文章适用于App混合H5方式调用手机精确定位,打包时需要选择GPS位置权限,手机获取定位过程中会弹出是否允许定位的权限提示。 …...

Go指针取址问题:循环后每次都拿到相同内容
例子: func main() {yourList : [...]int{1, 2, 3}yourMap1 : make(map[int]*int)yourMap2 : make(map[int]*int)for key, value : range yourList {// 修改前yourMap1[key] &value// 修改后tmp : valueyourMap2[key] &tmpfmt.Println(value, &value…...

用Rust实现23种设计模式之简单工厂
在 Rust 中,可以使用结构体和 trait 来实现工厂方法模式。工厂方法模式是一种创建型设计模式,通过定义一个创建对象的接口,让子类决定实例化哪个类。下面是一个简单的示例,展示了如何使用 Rust 实现工厂方法模式: // …...

SpringBoot + minio实现分片上传、秒传、续传
什么是minio MinIO是一个基于Go实现的高性能、兼容S3协议的对象存储。它采用GNU AGPL v3开源协议,项目地址是https://github.com/minio/minio。 引用官网: MinIO是根据GNU Affero通用公共许可证v3.0发布的高性能对象存储。它与Amazon S3云存储服务兼容…...

logback 里面设置 自动删除3天之前的日志
目录 1 实现 1 实现 要实现达到一定大小后将日志文件压缩,并删除三天前的日志数据,可以结合使用 SizeAndTimeBasedRollingPolicy 滚动策略和 DeleteOlderThan 选项来配置。下面是一个示例配置,实现日志文件达到一定大小后进行滚动和压缩&…...
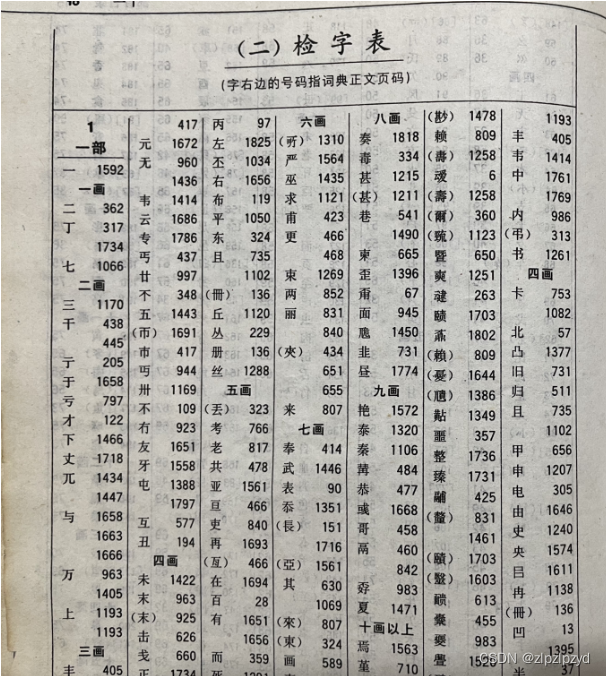
对于数据库查询索引和查字典索引的理解
之前面试问过我对于数据库索引的理解,这个问题不是具体的问题太宽泛,面试官也没进行引导,我不知道怎么回答,下面是结合查字典进行理解。 查字典 拿查字典举例,知道一个字怎么写但是不知道具体的意思以及发音ÿ…...
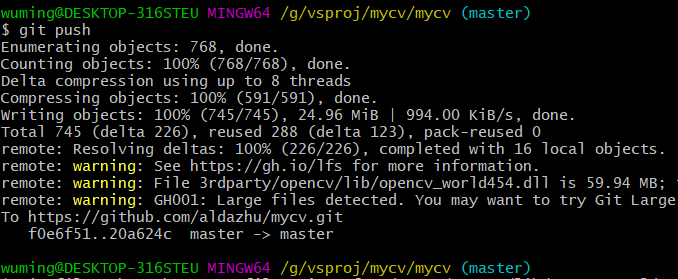
git删除已经提交的大文件
当你不小心把一个巨大的二进制文件提交到git仓库的时候,此时删除再提交也没有用了,大文件已经在仓库中留底了。另外比如需要删除某个需要保密的文件,都是相同的解决办法。 我本来想着把dll放在三方库里面提交到仓库里,省得在不同…...

【数据分析】pandas 一
目录 一,pandas简介: 二,pandas数据结构Series简介: 2.1 data为ndarray 2.2 data为字典 三,Serise切片操作: 四,Series性质: 4.1 Series类似于numpy,字典 4.2 矢量化操作和标…...

题解 | #G.Gcd# 2023牛客暑期多校6
G.Gcd 数论 题目大意 给定一个包含两个非负数的初始集合 S { x , y } S\{x,y\} S{x,y} 每次操作可以选定其中不相等的两个数 a , b a,b a,b ,并将 a − b a-b a−b 或 g c d ( a , b ) gcd(a,b) gcd(a,b) 置入集合 S S S ,其中 g c d ( 0 , a …...
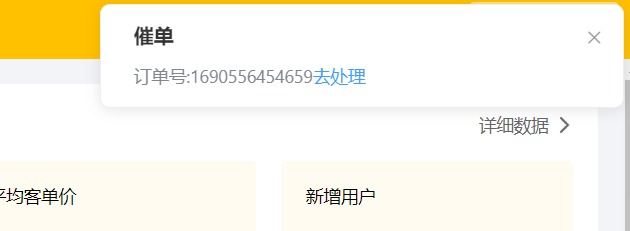
苍穹外卖day10——订单状态定时处理(Spring Task)、来单提醒和客户催单(WebSocket)
预期效果 对于超时没处理的需要定时程序处理。基于SpringTask实现。 来单提醒和客户催单。基于WebSocket实现。 Spring Task 介绍 Cron表达式 周几通常不能和日一起指定。 cron表达式在线生成器 在线Cron表达式生成器 入门案例 创建定时任务类 /*** 定义定时任务类*/ Slf4j…...
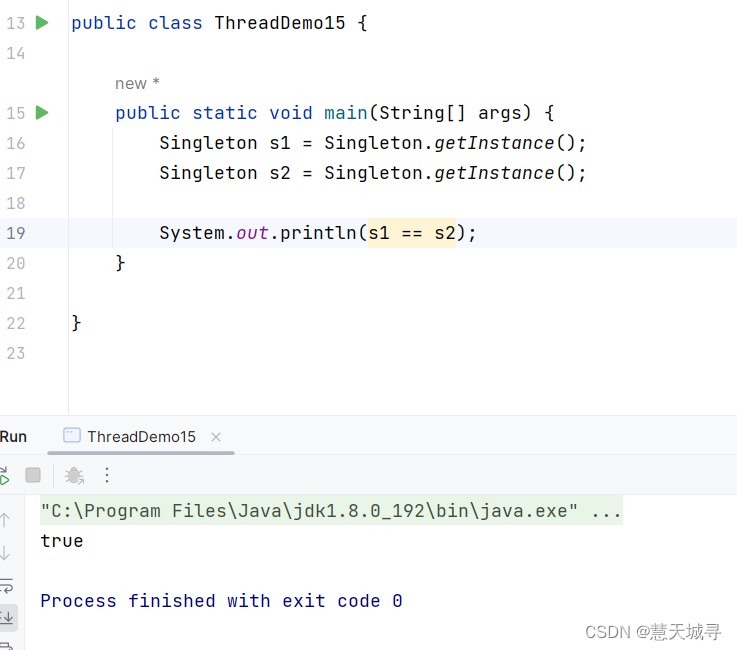
【多线程初阶】多线程案例之单例模式
文章目录 前言1. 什么是单例模式2. 饿汉模式3. 懒汉模式 --- 单线程版4. 懒汉模式 --- 多线程版5. 懒汉模式 --- 多线程改进版总结 前言 本文主要给大家讲解多线程的一个重要案例 — 单例模式. 关注收藏, 开始学习吧🧐 1. 什么是单例模式 单例模式是一种很经典的…...

跨境选品怎么选?建议独立站卖家收下这份利基产品查找攻略!
跨境电商平台现在可谓是火热发展中,独立站出海风口,其实选择的机会还真不少,相比国内电商的发展势头,看得出来,未来跨境电商的大门,对你而言,敞开着。选品这事儿,就像你上战场前挑选…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
