题解 | #G.Gcd# 2023牛客暑期多校6
G.Gcd
数论
题目大意
给定一个包含两个非负数的初始集合 S = { x , y } S=\{x,y\} S={x,y}
每次操作可以选定其中不相等的两个数 a , b a,b a,b ,并将 a − b a-b a−b 或 g c d ( a , b ) gcd(a,b) gcd(a,b) 置入集合 S S S ,其中 g c d ( 0 , a ) = a gcd(0,a)=a gcd(0,a)=a
可以操作任意次,问能否使得集合 S S S 包含非负数 z z z
前置知识点
裴蜀定理
解题思路
根据裴蜀定理,两个正整数辗转相减只能得到他们最大公约数的倍数//
因此对于 z z z ,判断其是否是 g c d ( x , y ) gcd(x,y) gcd(x,y) 的倍数即可
如果 z z z 是 g g g 的倍数,则可以通过以下操作得到 z z z :
- 将 g = g c d ( x , y ) g=gcd(x,y) g=gcd(x,y) 置入集合
- x x x 作为 g g g 的倍数,其加减任意次 g g g 便可得到任意 g g g 的倍数。
只能减不能加怎么办呢//先把 x x x 减到 − g -g −g 就好了
值得注意的是,本题的数据约束为非负数,这意味着需要对 0 0 0 的情况进行特判//
- 对于 z = 0 z=0 z=0 ,仅当 x , y x,y x,y 有 0 0 0 时有解
- 对于 x = 0 x=0 x=0 或 y = 0 y=0 y=0 ,仅当 z z z 与其中之一相等时有解(实际上这条也满足裴蜀定理//只是懒得重写 g c d gcd gcd 了)
参考代码
参考代码为已AC代码主干,其中部分功能需读者自行实现
void solve()
{ll x,y,z;cin >> x >> y >> z;if(x&&y&&z==0) {cout << NO;return;}if((x==0)||(y==0)) if(z==x||z==y) {cout << YES;return;} else {cout << NO;return;}ll g=gcd(x,y);if(z%g) cout << NO;else cout << YES;
}
相关文章:

题解 | #G.Gcd# 2023牛客暑期多校6
G.Gcd 数论 题目大意 给定一个包含两个非负数的初始集合 S { x , y } S\{x,y\} S{x,y} 每次操作可以选定其中不相等的两个数 a , b a,b a,b ,并将 a − b a-b a−b 或 g c d ( a , b ) gcd(a,b) gcd(a,b) 置入集合 S S S ,其中 g c d ( 0 , a …...
苍穹外卖day10——订单状态定时处理(Spring Task)、来单提醒和客户催单(WebSocket)
预期效果 对于超时没处理的需要定时程序处理。基于SpringTask实现。 来单提醒和客户催单。基于WebSocket实现。 Spring Task 介绍 Cron表达式 周几通常不能和日一起指定。 cron表达式在线生成器 在线Cron表达式生成器 入门案例 创建定时任务类 /*** 定义定时任务类*/ Slf4j…...
【多线程初阶】多线程案例之单例模式
文章目录 前言1. 什么是单例模式2. 饿汉模式3. 懒汉模式 --- 单线程版4. 懒汉模式 --- 多线程版5. 懒汉模式 --- 多线程改进版总结 前言 本文主要给大家讲解多线程的一个重要案例 — 单例模式. 关注收藏, 开始学习吧🧐 1. 什么是单例模式 单例模式是一种很经典的…...

跨境选品怎么选?建议独立站卖家收下这份利基产品查找攻略!
跨境电商平台现在可谓是火热发展中,独立站出海风口,其实选择的机会还真不少,相比国内电商的发展势头,看得出来,未来跨境电商的大门,对你而言,敞开着。选品这事儿,就像你上战场前挑选…...

[C++项目] Boost文档 站内搜索引擎(1): 项目背景介绍、相关技术栈、相关概念介绍...
项目背景 Boost库是C中一个非常重要的开源库. 它实现了许多C标准库中没有涉及的特性和功能, 一度成为了C标准库的拓展库. C新标准的内容, 很大一部分脱胎于Boost库中. Boost库的高质量代码 以及 提供了更多实用方便的C组件, 使得Boost库在C开发中会被高频使用 为方便开发者学…...

opencv-32 图像平滑处理-高斯滤波cv2.GaussianBlur()
在进行均值滤波和方框滤波时,其邻域内每个像素的权重是相等的。在高斯滤波中,会将中心点的权重值加大,远离中心点的权重值减小,在此基础上计算邻域内各个像素值不同权重 的和。 基本原理 在高斯滤波中,卷积核中的值不…...

Windows 环境Kubernetes安装
目录 前言 安装 Docker 安装 Kubernetes Windows 安装 kubectl 介绍 安装 开启 Kubernetes 前言 Docker作为当前最流行的容器化平台,为Kubernetes提供了强大的容器化技术基础。Kubernetes与Docker的结合,使得容器化应用程序在大规模集群中得以简…...
自建类ChatGPT服务:本地化部署与远程访问教程
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

常用SQL语句总结
SQL语句 文章目录 SQL语句1 SQL语句简介2 DQL(数据查询语句)3 DML(数据操纵语句)4 DDL(数据定义语句)5 DCL(数据控制语句)6 TCL(事务控制语句) 1 SQL语句简介…...
arm交叉编译lmbench
一、下载lmbench www.bitmover.com/lmbench 官网下载,http://www.bitmover.com/lmbench/lmbench3.tar.gz 我没有下载下来,找的别人的百度云下载 链接: https://pan.baidu.com/s/1tGo1clCqY-jQPN8G1eWSsg 提取码: f6jd 二、修改makefile 修改三个文件…...
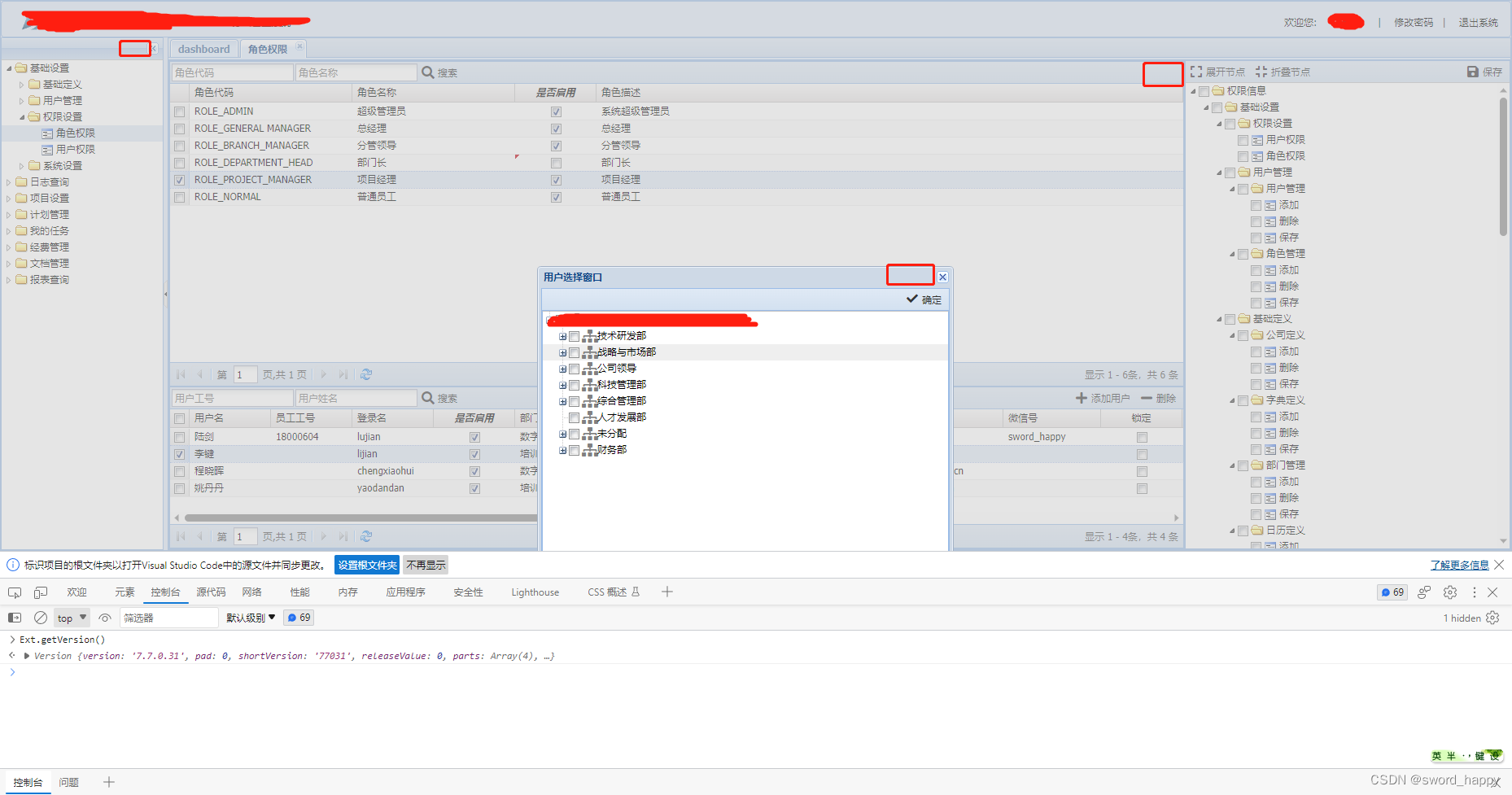
ExtJs 7.7.0 下载方法与去除trial水印
背景 最近发现Sencha ExtJs发布了ExtJs7.7.0版本,立刻下载了SDK包,许多朋友不知如何下载,如何去除右上角的trial水印。本文讲下相关下载技巧与方法。 下载SDK 首先需要申请试用,申请地址如下,需要注意可能需要梯子&…...

Android11开发规划
文章目录 规划总结规划 提示:这里可以添加本文要记录的大概内容: 从本文开始,会介绍如何移植瑞芯微提供的Android11源码到自己的RK3568的板子上 下面是整个Android开发的规划: 包括以下部分: … 一、移植部分 下载编译瑞芯微提供的源码 瑞芯微原厂源码目录介绍...

活动隔断在现在酒店运用的方式
活动隔断是一种在酒店内部划分空间的方式,用于实现不同活动的隔离和隐私。现代酒店常用的活动隔断方式有以下几种: 1. 固定隔断:使用墙体、固定屏风或者板材等材料,将空间划分为不同的房间或区域。这种方式常用于划分客房、会议室…...
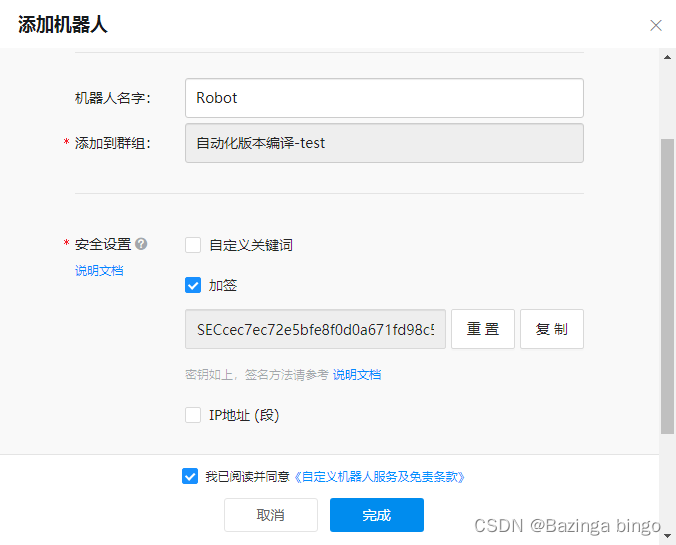
Jenkins工具系列 —— 插件 钉钉发送消息
文章目录 安装插件 Ding TalkJenkins 配置钉钉机器人钉钉APP配置项目中启动钉钉通知功能 安装插件 Ding Talk 点击 左侧的 Manage Jenkins —> Plugins ——> 左侧的 Available plugins Jenkins 配置钉钉机器人 点击 左侧的 Manage Jenkins ,拉到最后 钉…...

LeetCode 26 题:删除有序数组的重复项
思路 在写这一个题时,我突然想到了Python中的 set()函数可能会有大用处,便选择了用Python写。 set()函数可以将列表转化为集合,集合会保证元素的单一性,所以会自动删去相同字符。 …...
)
优雅地切换node版本(windows)
文章目录 1、下载并安装nvm2、nvm的使用3、处理npm版本与nodejs版本不匹配问题(通常不会有这个问题) 1、下载并安装nvm 卸载已安装的node:控制面板-程序-找到node并卸载 通常在控制面板中卸载后,nodejs目录、环境变量、注册表就自…...

反诈:吴明军、黄亮领导的WIN生活资金盘,大家警惕防范此类诈骗
消息已经证实!“米粒”无法变现,数以万计的会员深套“315万民商城”,维权艰难,血汗钱无法讨回。 其实这一点笔者并不感到太意外,因为万民商城资金传销盘的定性之前就已经发文揭露过,并反复提醒大家小心警惕…...
)
shell、bash的关系及bash的特性(一)
一、概念 shell是壳,是运行在终端中的文本互动程序。Shell相当于是一个翻译,把我们在计算机上的操作命令,翻译为计算机可识别的二进制命令,传递给内核,以便调用计算机硬件执行相关的操作;同时,计…...
【问题随记】
ubuntu 14.04源更新(sources.list) deb http://mirrors.aliyun.com/ubuntu/ trusty main restricted universe multiverse deb http://mirrors.aliyun.com/ubuntu/ trusty-security main restricted universe multiverse deb http://mirrors.aliyun.com/ubuntu/ trusty-update…...

Stable Diffusion AI绘画学习指南【常用模型,采样器介绍】
常用采样器、目前有20个采样步骤越多每个步之间的降噪越小,减少采样过程中的截断误差,结果越好 学微分方程求解器 Euler(最简单的采样器,采样过程中不加随机噪声,根据采样计划来执行每个步骤中的噪声,并使…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
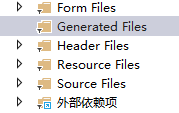
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...
