数学知识(二)
一、裴蜀定理
对于任意整数a,b,一定存在非零整数x,y,使得 ax + by = gcd(a,b)
#include<iostream>
#include<algorithm>using namespace std;int exgcd(int a,int b,int &x,int &y)
{if(!b){x = 1,y = 0;return a;}int d = exgcd(b,a % b,y,x);y -= a / b * x;return d;
}int main()
{int n;scanf("%d",&n);while(n --){int a,b,x,y;scanf("%d%d",&a,&b);exgcd (a,b,x,y);printf("%d%d\n",x,y);}return 0;
}二、高斯消元
步骤:枚举每一列,取列c
- 1、找到绝对值最大的一行
- 2、将该行换到最上面
- 3、将该行第一个数变为1(与该行其它数的比值不改变)
- 4、将下面所有行的第c列消为零
#include<iostream>
#include<cmath>
#include<algorithm>using namespace std;const int N = 110;
const double eps = 1e-6;int n;
double a[N][N];int gauss()
{int c,r;for(c = 0,r = 0; c < n;c ++){//找到绝对值最大的一行int t = r;for(int i = r; i < n; i ++)if(fabs(a[i][c]) > fabs(a[t][c])) t = i;if(fabs(a[t][c]) < eps) continue;//将该行换到最上方for(int i = c;i <= n;i ++) swap(a[t][i],a[r][i]);//将该行第一个数变为1for(int i = n;i >= c; i --) a[r][i] /= a[r][c];//将下面所有行消为0for(int i = r + 1;i < n;i ++)if(fabs(a[i][c]) > eps)for(int j = n;j >= c;j --)a[i][j] -= a[r][j] * a[i][c];r ++;}if(r < n){for(int i = r;i < n;i ++)if(fabs(a[i][n]) > eps)return 2; //无解return 1; //有无穷多组解}for(int i = n - 1;i >= 0;i --)for(int j = i + 1;j < n;j ++)a[i][n] -= a[i][j] * a[j][n];return 0; //存在唯一的解
}三、求组合数
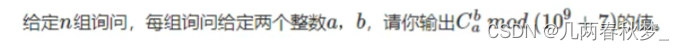
#include<iostream>
#include<cmath>
#include<algorithm>using namespace std;const int N = 2010,mod = 1e9 + 7;
int c[N][N];//初始化
void init()
{for(int i = 0;i < N;i ++)for(int j = 0;j <= i;j ++){if(!j) c[i][j] = 1;else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;}}
int main()
{init();int n;scanf("%d",&n);while(n --){int a,b;scanf("%d%d",&a,&b);printf("%d\n",c[a][b]);}return 0;
}
第二种方法:
#include<iostream>
#include<algorithm>
#include<cmath>using namespace std;typedef long long LL;
const int N = 100010,mod = 1e9 + 7;int fact[N],infact[N];int qmi(int a,int k,int p)
{int res = 1;while(k){if(k & 1) res = (LL) res *a % p;a = (LL)a * a % p;k >>= 1;}return res;
}int main()
{fact[0] = infact[0] = 1;for(int i = 1;i < N;i ++){fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i,mod - 2,mod) % mod;}int n;scanf("%d",&n);while(n --){int a,b;scanf("%d%d",&a,&b);printf("%d\n",(LL)fact[a] * infact[b] % mod * infact[a - b] % mod);}return 0;
}
相关文章:
数学知识(二)
一、裴蜀定理 对于任意整数a,b,一定存在非零整数x,y,使得 ax by gcd(a,b) #include<iostream> #include<algorithm>using namespace std;int exgcd(int a,int b,int &x,int &y) {if(!b){x 1,y 0;return a;}int d exgcd(b,a %…...
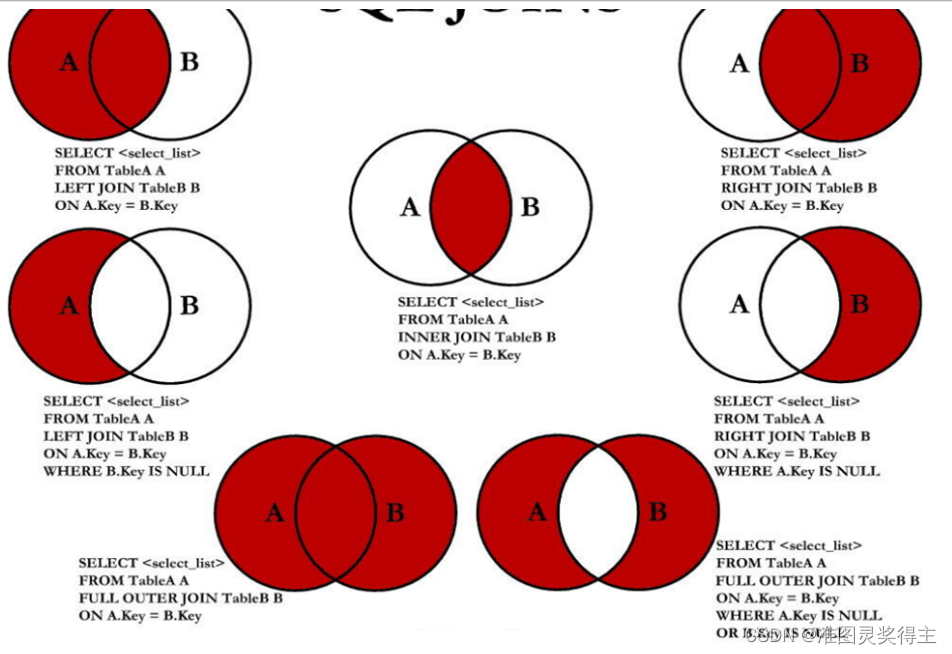
Java实现数据库表中的七种连接【Mysql】
Java实现数据库表中的七种连接【Mysql】 前言版权推荐Java实现数据库表中的七种连接左外连接右外连接其他连接 附录七种连接SQL测试Java测试转换方法类 Cla1类 Cla2类Cla3 最后 前言 2023-8-4 16:51:42 以下内容源自《【Mysql】》 仅供学习交流使用 版权 禁止其他平台发布时…...

452. 用最少数量的箭引爆气球
452. 用最少数量的箭引爆气球452. 用最少数量的箭引爆气球 有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。 一支弓箭可…...

HTML <rp> 标签
实例 一个 ruby 注释: <ruby> 漢 <rt><rp>(</rp>ㄏㄢˋ<rp>)</rp></rt> </ruby>浏览器支持 元素ChromeIEFirefoxSafariOpera<rp>5.05.538.05.015.0 Internet Explorer 9, Firefox, Opera, Chrome 以及 S…...

常见的设计模式(超详细)
文章目录 单例模式饿汉式单例模式懒汉式单例模式双重检索单例模式 工厂模式简单工厂模式工厂(方法)模式抽象工厂模式 原型模式代理模式 单例模式 确保一个类只有一个实例,并且自行实例化并向整个系统提供这个实例。 饿汉式单例模式 饿汉式单…...

Excel 超牛的格式调整汇总——你还在担心你做出来的表不好看吗
Excel格式调整技巧 绘图逆序绘制条形图设置条形图宽度 条件格式透视表上的条件格式 数字格式千分位逗号数字同时显示 K M 数据分列非重复计数区域透视图新增计算列隐藏行列快捷键其他小技巧 绘图 逆序绘制条形图 设置条形图宽度 条件格式 透视表上的条件格式 条件格式随切片…...

hyperf 十二、自动化测试
文档教程:Hyperf 用co-phpunit提供测试,在composer中测试。 "scripts": {"test": "co-phpunit --prepend test/bootstrap.php -c phpunit.xml --colorsalways", } 测试中使用Hyperf\Testing\Client模拟请求,该类调用Hyp…...

dblink简单使用
1.配置tns [oraclepg1 admin]$ cat tnsnames.ora 19c (DESCRIPTION (ADDRESS_LIST (ADDRESS (PROTOCOL TCP)(HOST 192.168.56.100)(PORT 1521)))(CONNECT_DATA (SERVICE_NAME orcl)))11g (DESCRIPTION (ADDRESS_LIST (ADDRESS (PROTOCOL TCP)(HOST 192.168.56…...
)
Typescript 第十一章 与JavaScript互操作(外参变量声明,外参类型声明,外参模块声明)
第十一章 与JavaScript互操作 本章讨论在实际开发中如何编写Typescript。有可能你真正把代码从无类型语言向Typescript迁移。也有可能要使用第三方库。 使用类型声明逐步从JavaScript迁移到Typescript使用第三方JavaScript和Typescript 11.1 类型声明 类型声明文件的扩展名…...

从0到1框架搭建,Python+Pytest+Allure+Git+Jenkins接口自动化框架(超细整理)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 接口测试是对系统…...

在windows配置redis的一些错误及解决方案
目录 Unable to connect to Redis; nested exception is io.lettuce.core.RedisConnectionException:用客户端Redis Desktop Manager一样的密码端口,是可以正常连接的,但是运行java程序之后使用接口请求就会报错 Unable to connect to Redis; nested e…...
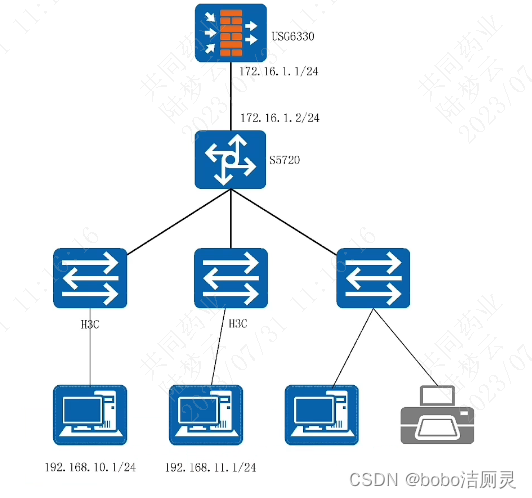
真机搭建中小网络
这是b站上的一个视频,演示了如何搭建一个典型的中小网络,供企业使用 一、上行端口:上行端口就是连接汇聚或者核心层的口,或者是出广域网互联网的口。也可理解成上传数据的端口。 二、下行端口:连接数据线进行下载的端…...
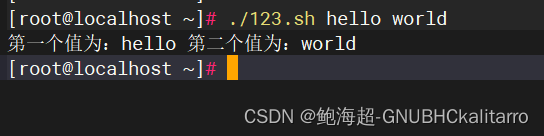
Linux:shell脚本:基础使用(1)
Shell的作用 命令解释器,“翻译官”,介于系统内核与用户之间,负责解释命令行 用户的登录Shell 登录后默认使用的Shell程序,一般为 /bin/bash 不同Shell的内部指令、运行环境等会有所区别 cat /etc/shells 编写第一个Shell脚本 …...
carla中lka实现(一)
前言: 对于之前项目中工作内容进行总结,使用Carla中的车辆进行lka算法调试,整体技术路线: ①在Carla中生成车辆,并在车辆上搭载camera,通过camera采集图像数据; ②使用图像处理lka算法&#…...
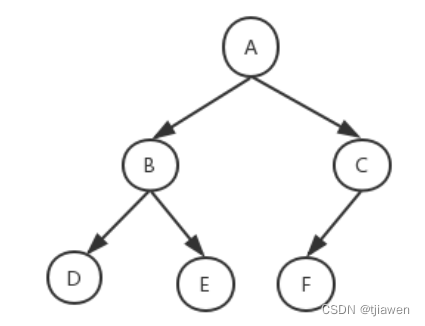
常见的数据结构(顺序表、顺序表、链表、栈、队列、二叉树)
线性表(Linear List) 1.什么是线性表 2.线性表的特点 3.线性表的基本运算 顺序表 1.什么是顺序表 2.时间复杂度: 链表 1.什么是链表 2.单向链表 3. 双向链表 4.ArrayList和LinkedList的使用 栈Stack 1.什么是栈 2.栈的基本方法 队列…...
(12)理解委托,反射,Type,EvenInfo,插件, 组合枚举,BindingFlags,扩展方法及重载,XML认识
一、复习委托事件 1、委托复习。 private delegate int MyDelegate(int a, int b); //1.定义委托类型private static void Main(string[] args){MyDelegate md new MyDelegate(AddDelegate);//2.声明委托变量int result md(1, 2);//3.调用委托Console.WriteLine(result);Cons…...

软件建设方案技术方案实施方案密码评测方案等保测评方案人员培训方案项目建设与运行管理项目招标方案模板目录
第一章 项目概述 1.项目名称(包含项目全称和简称) 2.项目建设单位及负责人、项目责任人 3.项目建设依据 (1)政策依据(主要从国家、省、市、行业部门相关的政策文件要求等方面进行描述) (2)技术标准 4.项目建设目标、建设任务 5.项目主要建设内容、规模、建设周期…...

pytorch中torch.einsum函数的详细计算过程图解
第一次见到 rel_h torch.einsum(“bhwc,hkc->bhwk”, r_q, Rh)这行代码时,属实是懵了,网上找了很多博主的介绍,但都没有详细的说明函数内部的计算过程,看得我是一头雾水,只知道计算结果的维度是如何变化的…...
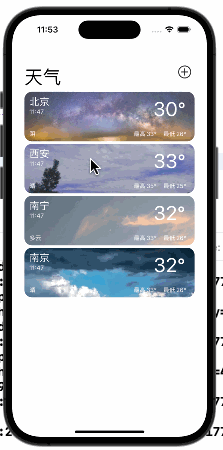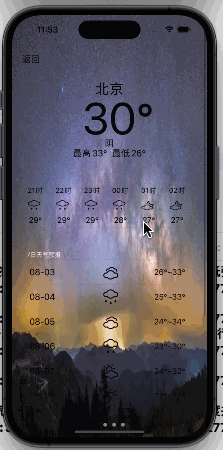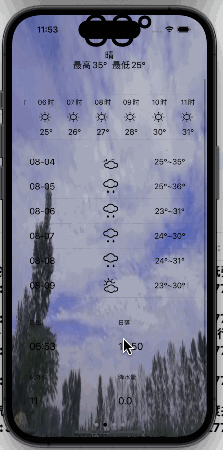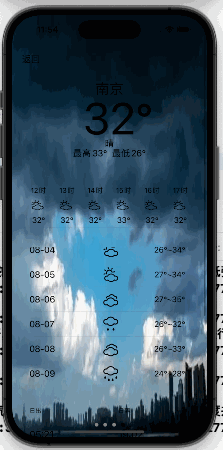
【iOS】App仿写--天气预报
文章目录 前言一、首页二、搜索界面三、添加界面四、浏览界面总结 前言 最近完成了暑假的最后一个任务——天气预报,特此记录博客总结。根据iPhone中天气App的功能大致可以将仿写的App分为四个界面——首页,搜索界面,添加界面,浏…...
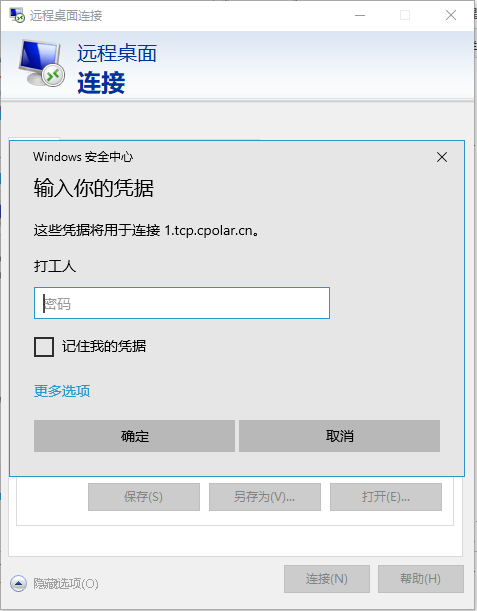
快速远程桌面控制公司电脑远程办公
文章目录 第一步第二步第三步 远程办公的概念很早就被提出来,但似乎并没有多少项目普及落实到实际应用层面,至少在前几年,远程办公距离我们仍然很遥远。但2019年末突如其来的疫情,着实打了大家一个措手不及。尽管国内最初的大面积…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
