静态代码审计插件 snyk 使用教程
目录
1、vscode 插件安装
2、手动生成 token
3、自动分析
1、vscode 插件安装
2、手动生成 token
点击登录链接:
相关文章:

静态代码审计插件 snyk 使用教程
目录 1、vscode 插件安装 2、手动生成 token 3、自动分析 1、vscode 插件安装 2、手动生成 token 点击登录链接:...

从“服务”,到“赋能”,日日顺再次定义供应链生态建设
在众多不确定因素的交织下,当下的供应链企业变革呈现出前所未有的紧迫感。一体化、全链路的趋势,为企业的发展指明方向,与此同时数字化与科技化开始承托供应链管理能力的升级与变革。 2月15日,由日日顺供应链、运联智库联合举办的…...
MySQL(一):B+ Tree,索引以及其优点, 索引实战, 聚簇索引和非聚簇索引, 最左匹配,索引失效
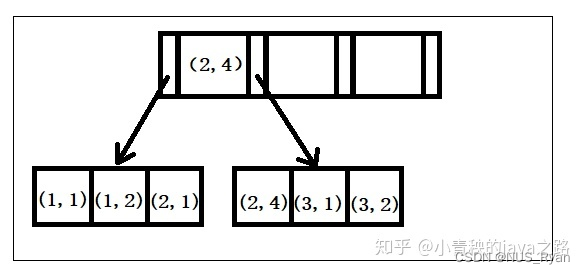
文章目录一、B TreeB Tree相比于红黑树的优点1. B树有更低的树高2. B树更符合磁盘访问原理二、MySQL索引2.1 B Tree索引2.2 哈希索引2.3 全文索引2.4 空间数据索引三、索引的优点以及什么时候需要使用索引什么时候需要使用索引四、索引实战建立普通索引建立唯一索引建立主键索引…...

06:进阶篇 - Hello,CTK!
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 在接触任何语言时,我们总能看到“Hello,World!",它的中文意思是“你好,世界!”。由于简洁、实用,所以非常著名。 为了延续这个优良传统并迎接 CTK,在演示第一个插件时,我们使用“Hello,CTK!&qu…...

SpringCloud(一)注册中心
注册中心eureka服务端客户端负载均衡nacos服务端客户端nacos分级存储模型配置集群属性nacos环境隔离-namespace临时实例和非临时实例Eureka和Nacos的异同负载均衡策略饥饿加载eureka 服务端 依赖 <!-- eureka注册中心服务端依赖--><dependencies><depe…...

centos7环境配置
Python Centos7中自带的python2,如果要是用python3,就需要自己安装了,因为yum源中没有python3,需要下载包进行源码编译安装。 安装步骤 1、安装python3相关依赖包 yum -y install zlib-devel bzip2-devel openssl-devel nc…...
如何解锁华为手机PIN/图案/指纹/人脸锁?
您的手机存储主要数据,因此为您的设备设置安全代码让您高枕无忧。屏幕和生物识别锁可在手机丢失时保护您的手机,并使其在被盗时无法访问。每次您需要密码来解锁手机时,但如果您被锁在密码之外怎么办? 今天的话题将独家帮助华为用…...

物理层基本介绍
corset 0 告诉下行初始带宽是多少 initail DL BWP, 4g 是20M带宽,5G是FR1 如果5G是全带宽的话,手机很快就会没电了。 告诉手机带宽会分布在某一个带宽里面去,将手机的带宽调整就行。 DCI,告诉手机,未来的某一个时刻&a…...

数据库原理及应用期末复习汇总(附某高校期末真题试卷)
文章目录《数据库原理及应用》试题1一、选择题(共35分)二、填空(每空1分,共20分)三、T-SQL综合题(共35分)四、综合应用题(共10分)《数据库原理及应用》试题2一、选择题(共35分)二、填空…...
)
mummerplot gnuplot 安装(nucmer)
可用ref:https://blog.sciencenet.cn/home.php?modspace&uid2970729&doblog&id1174911 下载稳定老版本gnuplot v4.6.2 mkdir gnuplot && cd gnuplot wget https://sourceforge.net/projects/gnuplot/files/gnuplot/4.6.2/gnuplot-4.6.2.tar…...

怎样做校园外卖配送系统创业?打造一体化服务校园平台如何进行?
在大学校园里,兼职赚钱、勤工俭学、自主创业是一种普遍现象。如今,大学校园在大力支持在校生自主创业。比如用校园外卖配送系统创业,不仅可以丰富校园生活,接触人和事,还可以积累经验。 怎样做校园外卖配送系统平台&am…...

MySQL(三):切分,主从复制,读写分离
文章目录一、切分水平切分垂直切分水平切分策略二、主从复制三、读写分离一、切分 水平切分 水平切分又称为sharding,它是将同一个表中的记录拆分到多个结构相同的表中。当一个表的数据不断增多的时候,sharding是必然的选择,它可以将数据分布到集群的不…...
王道考研——计算机网络(第一章 计算机网络体系结构)
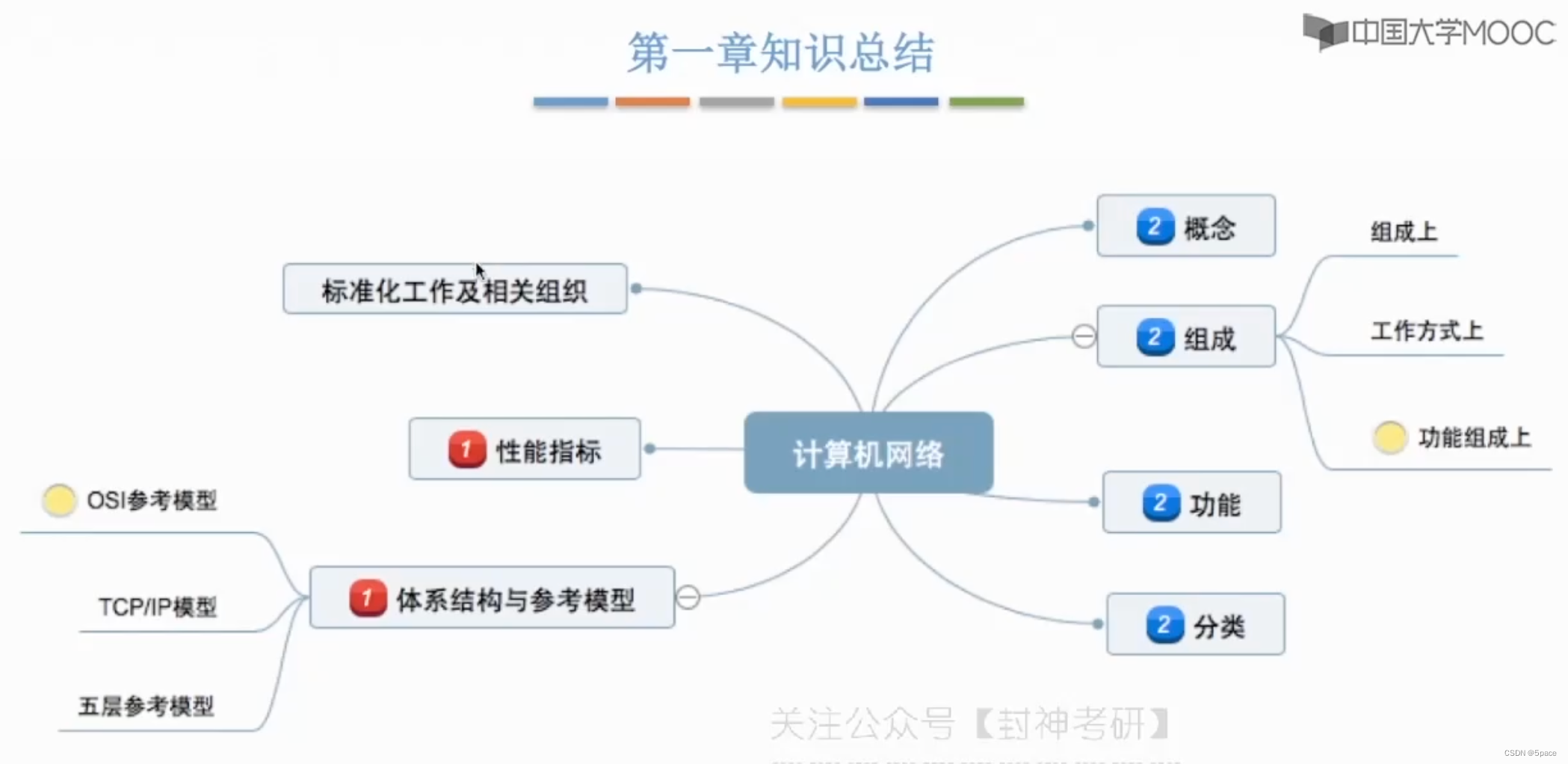
1.0认识计算机网络 在下载电影(不会出现乱序问题)和微信收发消息(比如表情包乱序了)所使用的协议是不同的 1.1-1概念和功能 (1)计算机网络的概念 (2)计算机网络的功能 (…...
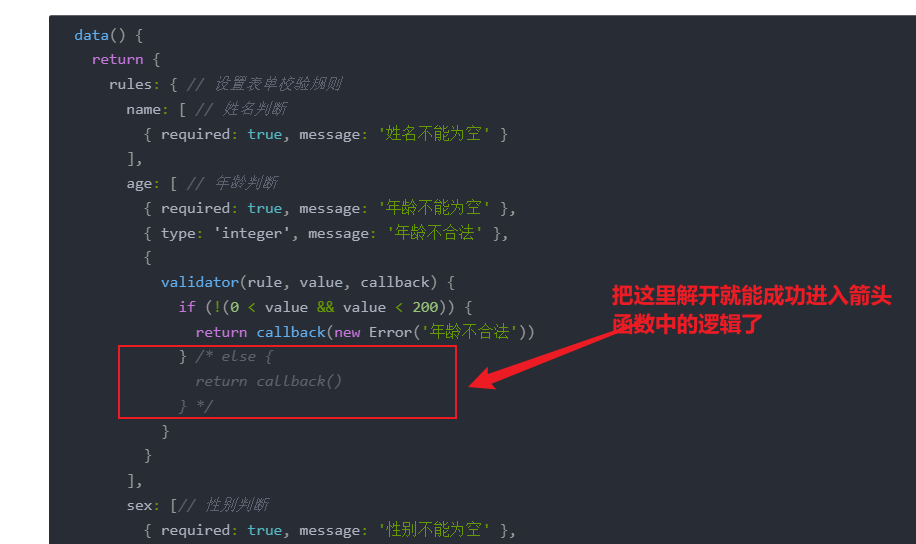
ElementUI中为什么使用this.$refs.form.validate验证成功却直接跳过
ElementUI中为什么使用this.$refs.form.validate验证成功却直接跳过 问题背景 在写一个Vue练手项目时,我使用rulse对表单中用户输入的数据进行校验,但莫名奇妙就发现:当我点击提交表单时,表单中的数据都验证成功了,但是…...

全期望值定理与全方差定理
全期望值定理(law of total expectation)比较熟悉,竟然还有个全方差定理(law of total variance),关于条件期望与条件方差的,总结一下。 1. 全期望值定理 随机变量 XXX 关于另外一个随机变量 …...
)
股票的最大利润 AcWing (JAVA)
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖 一次 该股票可能获得的利润是多少? 例如一只股票在某些时间节点的价格为 [9,11,8,5,7,12,16,14]。 如果我们能在价格为 5 的时候买入并在价格为 16 时卖出,则能收获最大的利润 11。…...

Go 语言函数调用参数传递规则
1. 调试环境Go 版本:1.19.3Gdb 版本:12.1CPU 架构:amd64Linux 发行版:Ubuntu 22.04Linux 内核版本:5.15.0-482. 函数调用参数传递规则版本变化在 Go 中函数间进行调用时,主调(caller)…...

二分查找【零神基础精讲】
来源0x3f:https://space.bilibili.com/206214 文章目录二分查找[34. 在排序数组中查找元素的第一个和最后一个位置](https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/)[162. 寻找峰值](https://leetcode.cn/problems/find-p…...

「计算机组成原理」数据的表示和运算(上)
文章目录一、进位计数制1.1 其他进制转十进制1.2 十进制转其他进制1.3 二进制、八进制和十六进制1.3 真值和机器数二、BCD码2.1 8421码2.2 余3码2.3 2421码三、整数的表示和运算3.1 无符号整数3.1.1 无符号整数的表示3.1.2 无符号整数的运算3.2 有符号整数3.2.1 有符号整数的表…...

分层,均质,稀薄燃烧
均质燃烧: 只能使用火花点燃。 即为普通燃烧方式,燃料和空气混合形成一定浓度的可燃混合气(厂家自配),整个燃烧室内混合气的空燃比是相同的,经火花塞点燃燃烧。这种燃烧方式使燃料和空气充分混合,燃料完全燃烧,从而获得大的输出功率。为使混合…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
