排序进行曲-v4.0
小程一言
这篇文章是在排序进行曲3.0之后的续讲,
这篇文章主要是对快速排序进行细致分析,以及操作。
希望大家多多支持
快速排序
基于分治的思想。它的基本思想是通过一趟排序将待排序的记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,然后再分别对这两部分记录进行排序,从而达到整个序列有序的目的。
步骤
详细解释
选择基准元素:从待排序序列中选择一个元素作为基准元素。一般可以选择第一个元素、最后一个元素或者随
机选择一个元素作为基准元素。分割操作:根据基准元素,将待排序序列分割成两个子序列。一个子序列中的元素都小于基准元素,另一个子
序列中的元素都大于基准元素。这个过程称为分割操作。递归排序:对两个子序列分别进行快速排序,直到子序列的长度为1或者0,即子序列已经有序。合并结果:将排序好的两个子序列合并,即将左子序列、基准元素和右子序列依次拼接起来,得到最终的有序
序列。
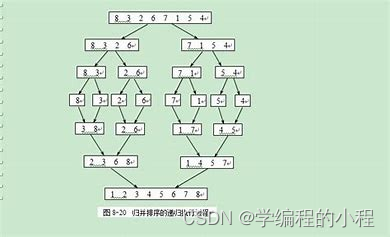
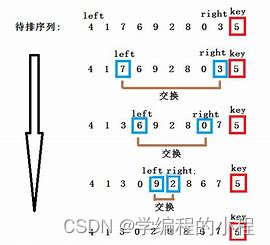
具体步骤
选择基准元素,假设选择第一个元素作为基准元素。设置两个指针,一个指向序列的第一个元素(左指针),一个指向序列的最后一个元素(右指针)。左指针向右移动,直到找到一个大于基准元素的元素。右指针向左移动,直到找到一个小于基准元素的元素。如果左指针小于右指针,则交换这两个元素。重复步骤3到步骤5,直到左指针大于等于右指针。将基准元素与左指针所指的元素进行交换,此时基准元素左边的元素都小于基准元素,右边的元素都大于基准元素。对基准元素左边的子序列和右边的子序列分别进行递归排序。合并结果,即将左子序列、基准元素和右子序列依次拼接起来,得到最终的有序序列。快速排序的时间复杂度为O(nlogn),其中n为待排序序列的长度。
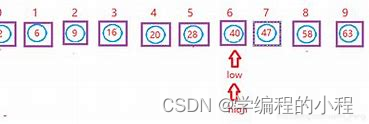
举例
假设有一个待排序序列为[5, 3, 8, 2, 1, 9, 4, 7, 6],下面以此序列为例进行快速排序。选择基准元素:选择第一个元素5作为基准元素。分割操作:根据基准元素5,将序列分割成两个子序列。比5小的元素放在左边,比5大的元素放在右边。分割后的序列为[2, 1, 4, 3] 5 [9, 8, 7, 6]。递归排序:对左右两个子序列进行递归排序。对左子序列[2, 1, 4, 3]进行快速排序,选择基准元素2。分割后的序列为[1] 2 [4, 3]。对右子序列[9, 8, 7, 6]进行快速排序,选择基准元素9。分割后的序列为[8, 7, 6] 9 []。继续对左子序列[4, 3]进行快速排序,选择基准元素4。分割后的序列为[3] 4 []。对右子序列[8, 7, 6]进行快速排序,选择基准元素8。分割后的序列为[6, 7] 8 []。继续对左子序列[3]进行快速排序,选择基准元素3。分割后的序列为[] 3 []。对右子序列[6, 7]进行快速排序,选择基准元素6。分割后的序列为[6] 7 []。合并结果:将排序好的子序列合并。最终的有序序列为[1, 2, 3, 4, 5, 6, 7, 8, 9]。
总结
通过以上步骤,我们可以看到快速排序将原始序列不断分割成两个子序列,并对子序列进行递归排序,最终将所
有子序列合并成一个有序序列。
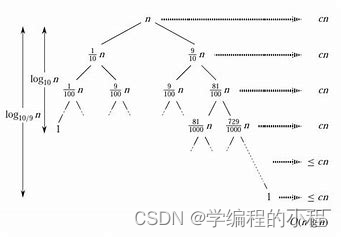
复杂度分析
快速排序的时间复杂度为O(nlogn),其中n为待排序序列的长度。
时间复杂度分析:
在最好情况下,每次分割操作都能将序列均匀地分成两部分,此时快速排序的时间复杂度为O(nlogn)。在最坏情况下,每次分割操作都将序列分成一个较小的子序列和一个较大的子序列,此时快速排序的时间复杂度为O(n^2)。最坏情况发生在待排序序列已经有序或基本有序的情况下。平均情况下,快速排序的时间复杂度仍然为O(nlogn)。这是因为在每一次分割操作中,将序列分成两部分的概率大致相等,每次分割操作的平均时间复杂度为O(n)。根据分治法的思想,快速排序的平均时间复杂度可以近似地看作是每次分割操作的时间复杂度乘以递归的层数,即O(nlogn)。
空间复杂度分析:
快速排序的空间复杂度为O(logn),主要是由于递归调用造成的栈空间使用。在最坏情况下,递归的层数为n,此时空间复杂度为O(n)。在平均情况下,递归的层数为logn,此时空间复杂度为O(logn)。

注意
总结起来,快速排序是一种高效的排序算法,平均情况下的时间复杂度为O(nlogn),空间复杂度为O(logn)。但在最坏情况下,时间复杂度可能达到O(n^2),需要额外的优化措施来避免最坏情况的发生。
应用场景
排序算法:快速排序是一种常用的排序算法,被广泛应用于各种排序任务中。它的时间复杂度较低,适用于处理大规模数据。数据库查询:在数据库中,经常需要对查询结果进行排序。快速排序可以在较短的时间内对查询结果进行排序,提高查询效率。文件系统排序:在文件系统中,需要对文件进行排序,以便更好地组织和管理文件。快速排序可以快速地对文件进行排序,提高文件系统的性能。搜索引擎排序:在搜索引擎中,需要对搜索结果进行排序,以便将相关度较高的结果排在前面。快速排序可以快速地对搜索结果进行排序,提高搜索引擎的效率。数据分析:在数据分析领域,经常需要对大量数据进行排序和统计。快速排序可以快速地对数据进行排序,为数据分析提供支持。

总结
快速排序是一种高效的排序算法,在大规模数据的排序和处理任务中具有广泛的应用场景。它的时间复杂度较低,适用于各种需要排序的场景。
实际举例
假设有一个学生信息表,包含学生的姓名、学号和成绩。我们希望按照成绩对学生进行排序,从高到低。快速排序可以很好地应用于这个场景。下面是一个使用快速排序对学生信息表按成绩排序的实际举例:原始数据:假设有以下学生信息表(按成绩从高到低排列):学生1:姓名-张三,学号-001,成绩-90
学生2:姓名-李四,学号-002,成绩-85
学生3:姓名-王五,学号-003,成绩-95
学生4:姓名-赵六,学号-004,成绩-80
选择基准元素:选择一个基准元素,可以是任意一个学生的成绩。假设选择学生3作为基准元素。分割操作:将学生信息表分割成两个子序列,一个序列包含所有成绩大于等于基准元素的学生,另一个序列包含所有成绩小于基准元素的学生。子序列1:学生3(成绩95)
子序列2:学生1(成绩90)、学生2(成绩85)、学生4(成绩80)
递归排序:对子序列1和子序列2分别进行递归排序,重复上述步骤,直到子序列只包含一个元素或为空。合并操作:将排序后的子序列合并,得到最终的有序序列。结果
排序后的序列:学生3(成绩95)、学生1(成绩90)、学生2(成绩85)、学生4(成绩80)总结
通过快速排序,我们成功将学生信息表按成绩从高到低排序。这个例子展示了快速排序在实际中的应用,通过选择基准元素、分割操作、递归排序和合并操作,可以高效地对大量数据进行排序。
代码实现
public class QuickSort {public static void main(String[] args) {int[] arr = {5, 2, 8, 9, 1, 3};quickSort(arr, 0, arr.length - 1);System.out.println(Arrays.toString(arr));}public static void quickSort(int[] arr, int low, int high) {if (low < high) {int pivotIndex = partition(arr, low, high);quickSort(arr, low, pivotIndex - 1);quickSort(arr, pivotIndex + 1, high);}}public static int partition(int[] arr, int low, int high) {int pivot = arr[high]; // 选择最后一个元素作为基准元素int i = low - 1;for (int j = low; j < high; j++) {if (arr[j] < pivot) {i++;swap(arr, i, j);}}swap(arr, i + 1, high);return i + 1;}public static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}结果
输出排序后的数组。运行结果为[1, 2, 3, 5, 8, 9],说明快速排序算法正确地对数组进行了排序。
解释
在上面的代码中,我们使用了递归的方式实现快速排序。首先定义了一个quickSort方法,接受一个数组和数组的起始位置和结束位置作为参数。在quickSort方法中,首先判断起始位置是否小于结束位置,如果是,则进行以下操作:调用partition方法,将数组分割成两个子序列,并返回基准元素的索引。对子序列1(起始位置到基准元素索引-1)和子序列2(基准元素索引+1到结束位置)分别递归调用quickSort方法,继续进行排序。递归结束后,数组将被排序。在partition方法中,我们选择最后一个元素作为基准元素。然后使用两个指针i和j,从起始位置开始遍历数组。如果遇到比基准元素小的元素,将i指针向后移动一位,并交换i和j指向的元素。遍历结束后,将基准元素与i+1位置的元素交换,确保基准元素的位置正确。
相关文章:

排序进行曲-v4.0
文章目录 小程一言快速排序步骤详细解释具体步骤 举例总结 复杂度分析时间复杂度分析:空间复杂度分析:注意 应用场景总结 实际举例结果总结 代码实现结果解释 小程一言 这篇文章是在排序进行曲3.0之后的续讲, 这篇文章主要是对快速排序进行细…...
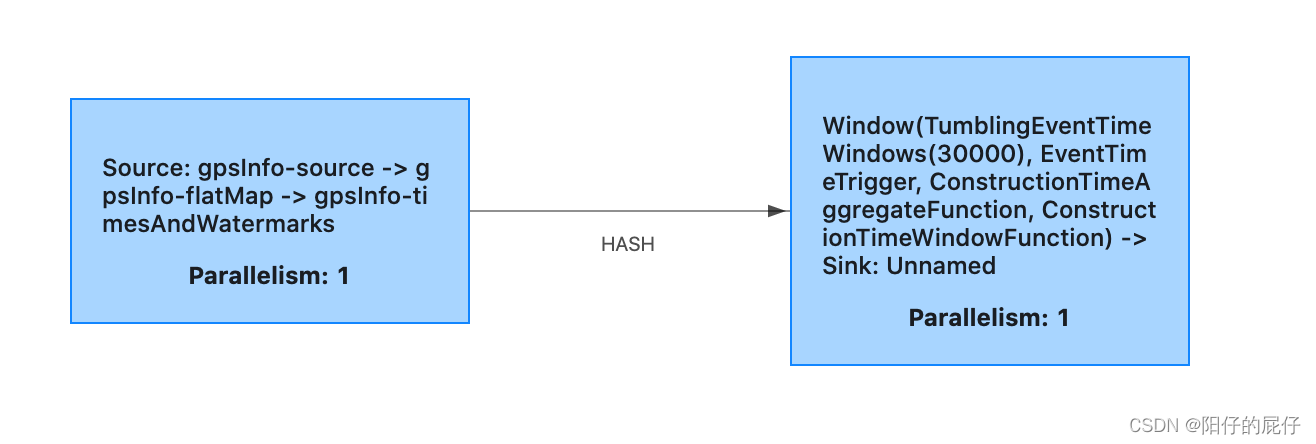
Flink 系列四 Flink 运行时架构
目录 前言 介绍 1、程序结构 1.1、Source 1.2、Transformation 1.3、Sink 1.4、数据流 2、Flink运行时组件 2.1、Dispatcher 2.2、JobManager 2.3、TaskManager 2.4、ResourceManager 3、任务提交流程 3.1、standalone 模式 3.2、yarn 模式 4、任务调度原理 4…...
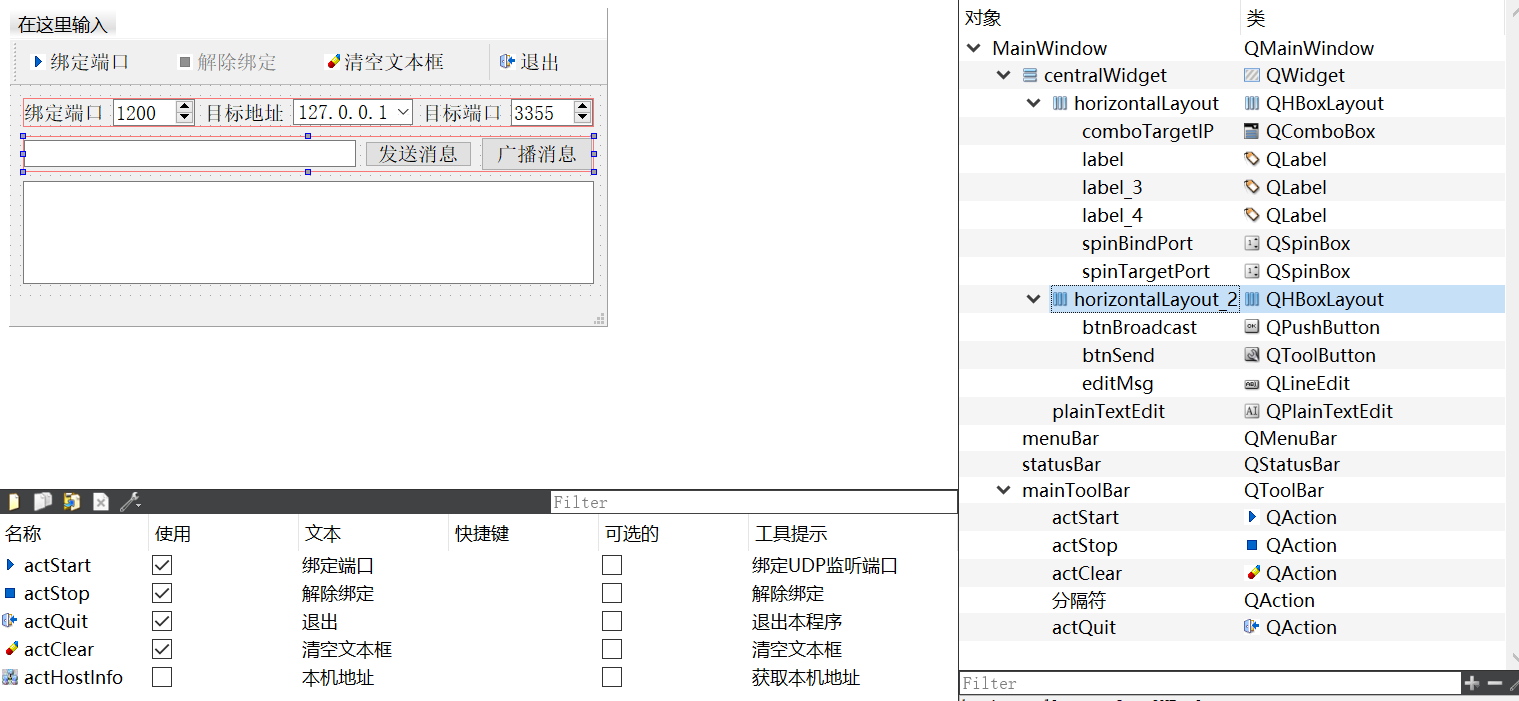
14-3_Qt 5.9 C++开发指南_QUdpSocket实现 UDP 通信_UDP 单播和广播
文章目录 1.UDP通信概述2. UDP 单播和广播2.1 UDP 通信实例程序功能2.2 主窗口类定义和构造函数2.3 UDP通信的实现2.4 源码2.4.1 可视化UI设计2.4.2 mainwindow.h2.4.3 mainwindow.cpp 1.UDP通信概述 UDP(User Datagram Protocol,用户数据报协议)是轻量的、不可靠的…...
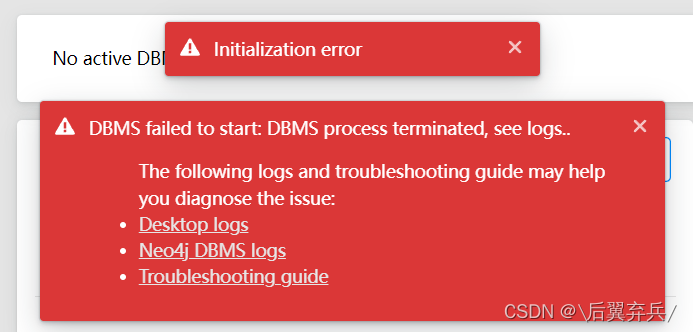
【知识图谱】图数据库Neo4jDesktop的安装图文详解(小白适用)
neo4j 的安装需要有jdk环境的支持。因此在安装Neo4j之前,需要安装Java JDK。 一.安装JDK 参考文章https://blog.csdn.net/weixin_41824534/article/details/104147067?spm1001.2014.3001.5502 二.Neo4j下载 进入Neo4j官网 选择下载中心 下滑选择Neo4j Deskto…...

kafka中幂等性producer和事务性producer
幂等性producer 在Kafka中,“幂等性生产者”的概念是指一种特性,它确保消息在生产者的发送操作被重试时仅发送一次。幂等性是一种重要的特性,因为在分布式系统中,网络问题或其他故障可能导致生产者发送的消息在传输过程中失败,从而需要重新发送。如果生产者没有幂等性保证…...
)
静态路由 (华为设备)
默认路由:当路由器 收到目标地址不在路由表中的数据包时,将会 全部 发送 到 默认路由所定义的吓一跳 ,作为位置地址 数据包的 最后求助方式,这就是默认路由器的功能,默认路由的使用,可以大大的节省系统资源…...
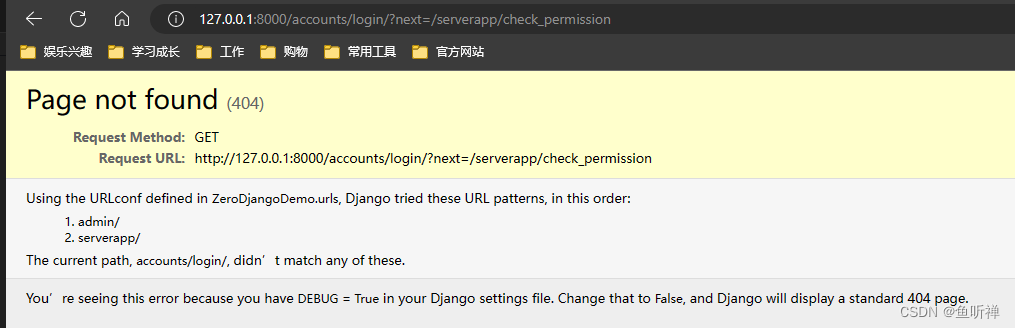
Django学习笔记-默认的用户认证系统(auth)
一、Django默认的用户认证系统 Django 自带一个用户验证系统。它负责处理用户账号、组、权限和基于cookie的用户会话。 Django 验证系统处理验证和授权。简单来说,验证检验用户是否是他们的用户,授权决定已验证用户能做什么。这里的术语验证用于指代这…...

[SQL挖掘机] - 存储过程
介绍: 当你在sql中需要多次执行相同的一组sql语句时,存储过程是一个非常有用的工具。它是一段预先定义好的sql代码块,可以被命名并保存在数据库中,以便重复使用。 存储过程可以包含多个sql语句、逻辑流程、条件判断和循环等,可以…...

MySQL8.0.32详细安装教程(奶妈级手把手教你安装)
MySQL安装详解 前言 对于无论是刚开始接触编程的小伙伴,还是有了几年工作经验的程序猿(程序媛)来讲,数据库的安装一直都是一个比 较复杂的过程,安装完成以后可能会记得一段时间,但是等到我们换了一台电脑或…...
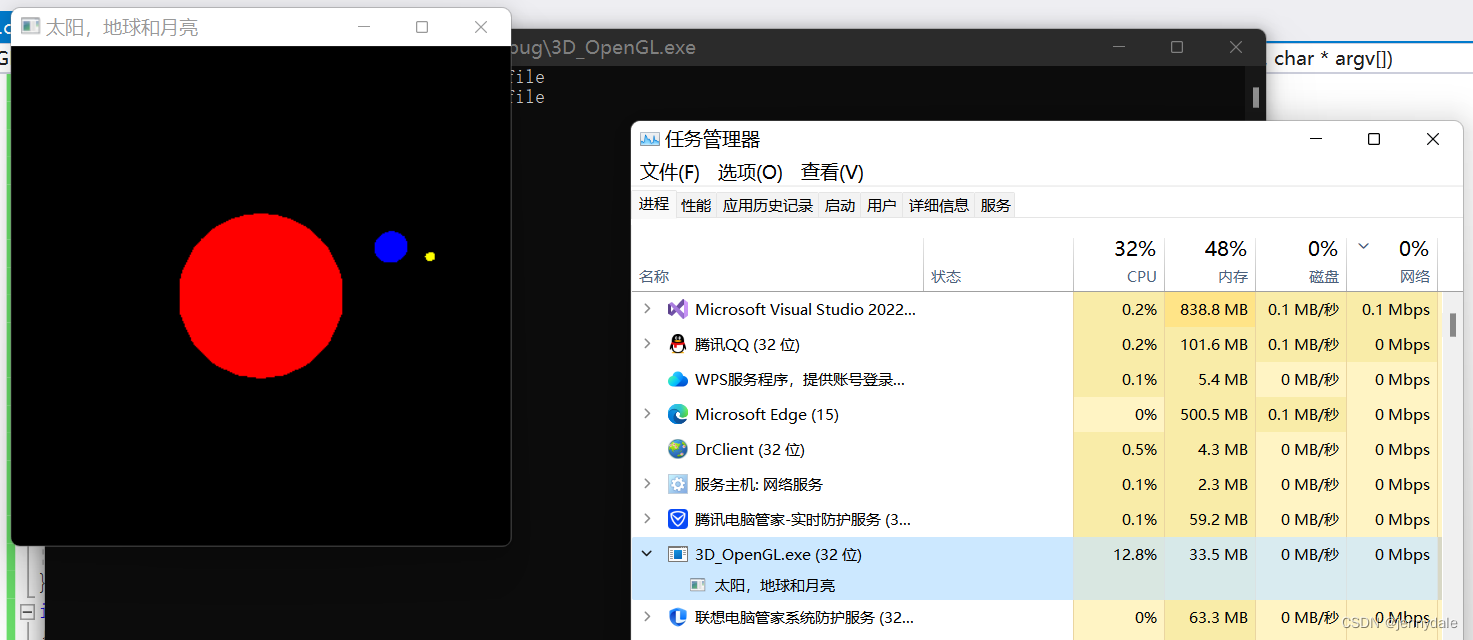
glut太阳系源码修改和对cpu占用观察
#include <GL/glut.h> static int day 100; // day 的变化:从 0 到 359 void myDisplay(void) {//glEnable(GL_DEPTH_TEST);glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluPerspective(75, 1, 1, 40…...

掌握NLTK:Python自然语言处理库中级教程
在之前的初级教程中,我们已经了解了NLTK(Natural Language Toolkit)的基本用法,如进行文本分词、词性标注和停用词移除等。在本篇中级教程中,我们将进一步探索NLTK的更多功能,包括词干提取、词形还原、n-gr…...

Go语言的崛起:探究越来越多公司选择Go语言的原因和优势
🌷🍁 博主猫头虎 带您 Go to Golang Language.✨✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~…...

MongoDB 6.0.8 安装配置
一、前言 MongoDB是一个基于分布式文件存储的数据库。由C语言编写。旨在为WEB应用提供可扩展的高性能数据存储解决方案。在高负载的情况下,添加更多的节点,可以保证服务器性能。 MongoDB 将数据存储为一个文档,数据结构由键值(key>value…...

无涯教程-Lua - nested语句函数
Lua编程语言允许在另一个循环中使用一个循环。以下部分显示了一些示例来说明这一概念。 nested loops - 语法 Lua中嵌套for循环语句的语法如下- for init,max/min value, increment dofor init,max/min value, incrementdostatement(s)endstatement(s) end Lua编程语言中的…...
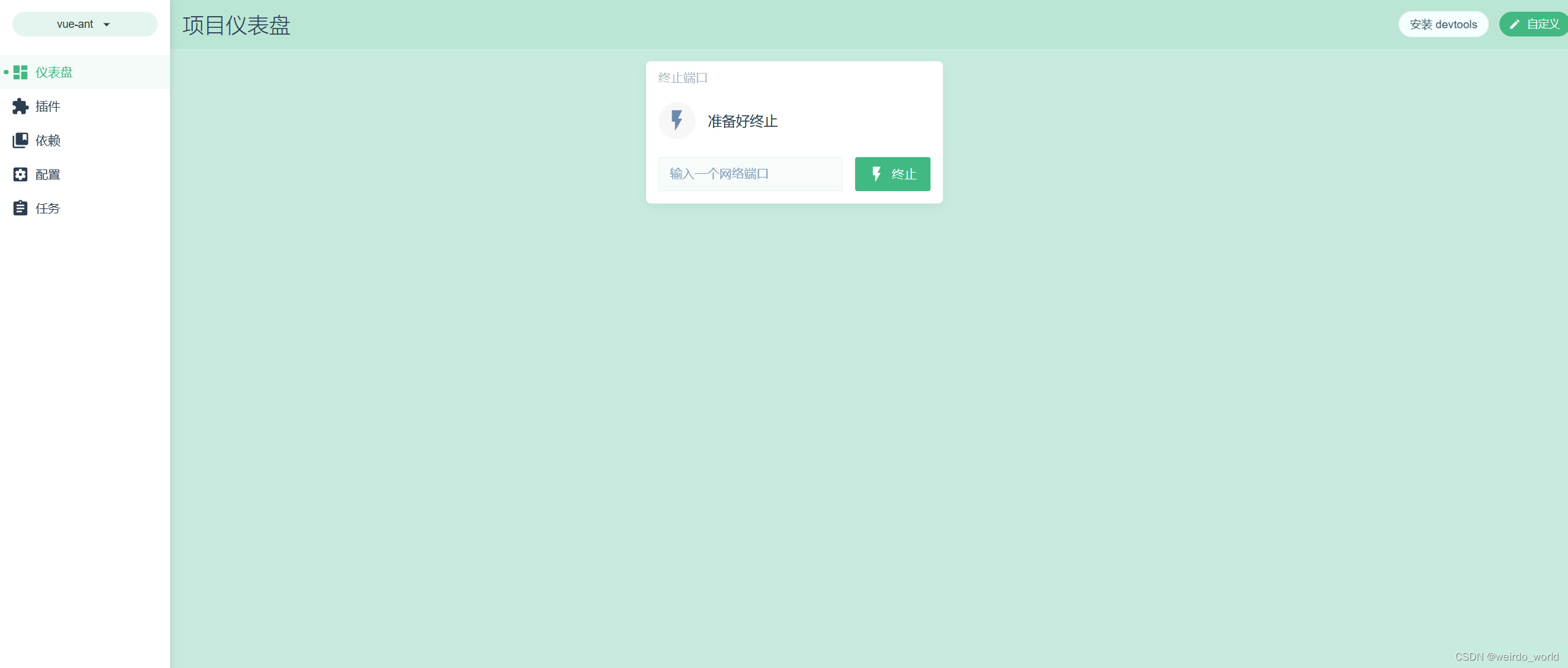
如何使用vue ui创建一个项目?
首先打开cmd 输入vue ui 等待浏览器打开一个窗口,按照下图操作 在"功能页面"中,各个插件代表以下意思: Babel:Babel是一个JavaScript编译器,用于将ES6代码转换为向后兼容的JavaScript版本,以确保…...
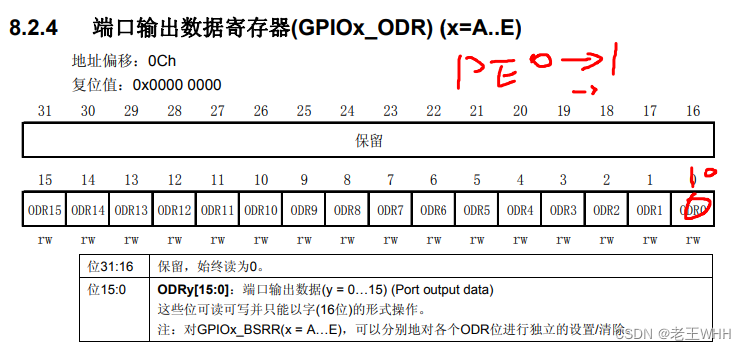
STM32——LED内容补充(寄存器点灯及反转的原理)
文章目录 点灯流程开时钟配置IO关灯操作灯反转宏定义最后给自己说 本篇文章使用的是STM32F103xC系列的芯片,四个led灯在PE2,PE3,PE4,PE5上连接 点灯流程 1.开时钟 2.配置IO口 (1)清零指定寄存器位 (2)设置模式为推挽输…...

使用Spring Boot和EasyExcel的导入导出
在当今信息化社会,数据的导入和导出在各种业务场景中变得越来越重要。为了满足复杂的导入导出需求,结合Java编程语言、Spring Boot框架以及EasyExcel库,我们可以轻松地构建出强大而灵活的数据处理系统。本文将引导您通过一个案例学习如何使用…...
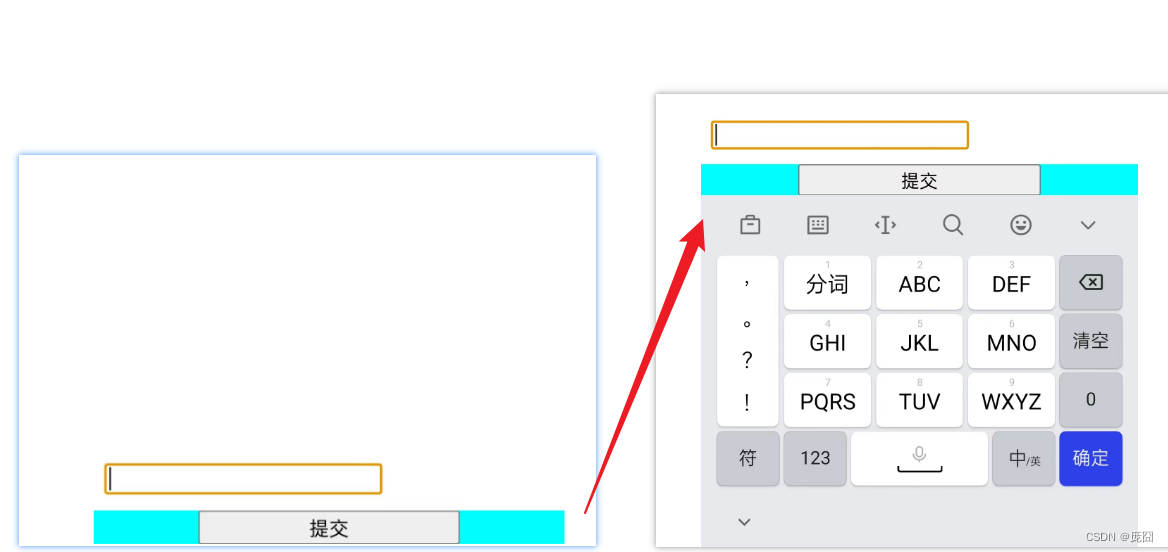
【H5移动端】常用的移动端方案合集-键盘呼起、全面屏适配、图片大小显示、300ms点击延迟、首屏优化(不定期补充~)
文章目录 前言键盘呼起问题靠近底部的输入项被键盘遮挡底部按钮被顶上去 全面屏适配图片大小显示问题解决300ms延迟首屏优化 前言 这篇文章总结了我在工作中做H5遇到的一些问题,包括我是怎么解决的。可能不是当下的最优解,但是能保证解决问题。 单位适…...
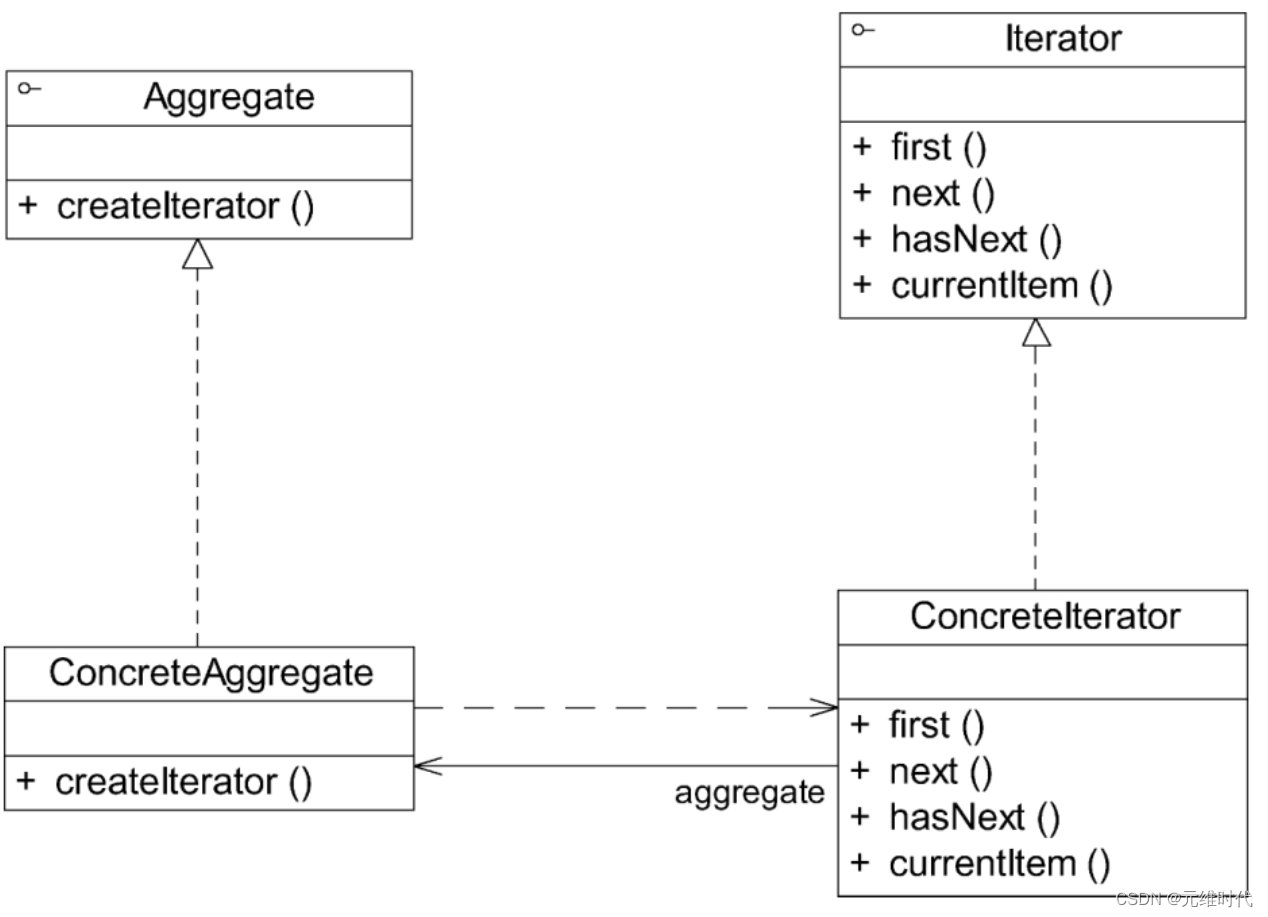
迭代器模式——遍历聚合对象中的元素
1、简介 1.1、概述 在软件开发时,经常需要使用聚合对象来存储一系列数据。聚合对象拥有两个职责:一是存储数据;二是遍历数据。从依赖性来看,前者是聚合对象的基本职责;而后者既是可变化的,又是可分离的。…...

亿赛通电子文档安全管理系统远程命令执行
人这一生,不是看你贫穷和富有,而是看你都做了些啥。 漏洞描述 亿赛通电子文档安全管理系统存在远程命令执行漏洞,攻击者通过构造特定的请求可执行任意命令 漏洞复现: 访问url: 构造payload请求 POST /solr/flow/d…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
