Nodejs环境搭建和配置
Nodejs环境的搭建和配置
1、下载
官网:http://nodejs.cn/download/,选择windows64位 msi文件
2、安装和配置环境
双击安装之后,配置环境变量:
①系统变量那边创建NODE_PATH变量,值为nodejs文件夹的node_modules文件夹路径
D:\Envirenment\nodejs\node_modules //这是我的
②Path变量里面添加两条变量:
D:\Envirenment\nodejs\ //nodejs文件夹路径
和
%NODE_PATH%
环境变量配置好之后,cmd打开终端,查看nodejs和npm的版本,如果跳出版本,说明安装成功
node -v
npm -v
随后在终端执行下面的命令:
npm config set prefix "D:\Envirenment\nodejs\node_global" //提前创建好文件夹,在nodejs文件夹目录下创建就行
npm config set cache "D:\Envirenment\nodejs\node_cache"
配置好之后,更改镜像源:
npm config set registry https://registry.npm.taobao.org //改成国内的,下载快
查看镜像设置情况:
npm get registry
安装Vue脚手架:
npm install -g@vue/cli
到这里,nodejs的环境就大体搭建完了,还有一些细节配置本人就没有去研究。
参考文章:
Vue开发实例(01)之环境搭建nodejs与运行第一个Vue项目
相关文章:

Nodejs环境搭建和配置
Nodejs环境的搭建和配置 1、下载 官网:http://nodejs.cn/download/,选择windows64位 msi文件 2、安装和配置环境 双击安装之后,配置环境变量: ①系统变量那边创建NODE_PATH变量,值为nodejs文件夹的node_modules文…...
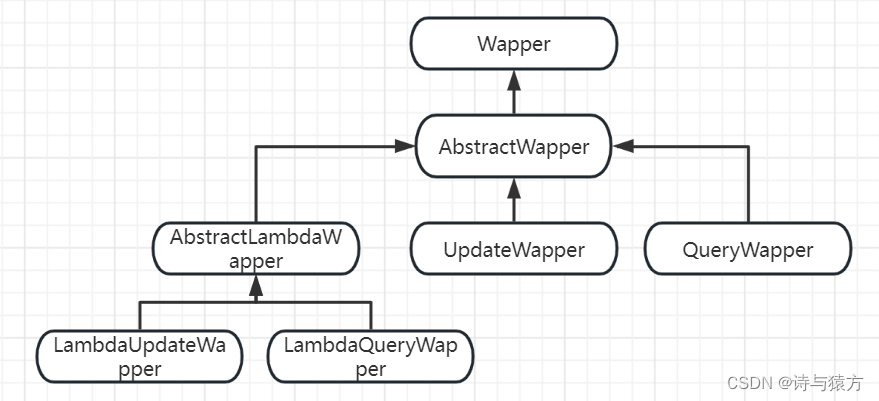
MybatisPlus------条件构造器Wrapper以及QueryWrapper用法(七)
MybatisPlus------条件构造器Wapper(七) Wrapper:条件构造器抽象类,最顶端父类 AbstarctWrapper:用于查询条件封装,生成sql的where条件。 QueryWrapper:查询条件封装(可以用于查询、删除&#x…...
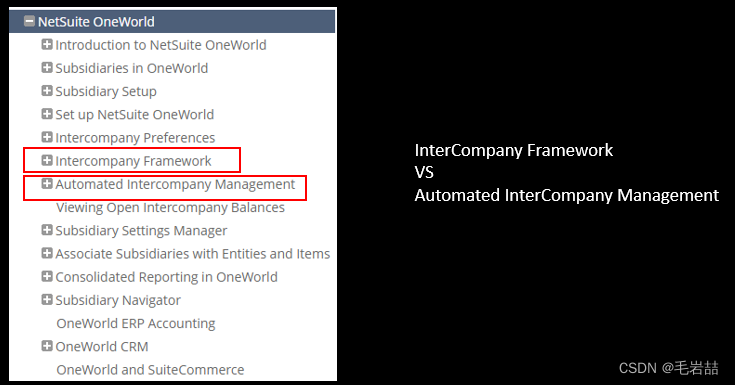
NetSuite Intercompany Framework 101
今朝,谈一谈Intercompany Framework,这是一个彰显NetSuite市场野心的基础功能框架。从20.2开始逐渐浮出水面,虽然经过过往的几个版本,不断推出组成功能,但目前仍然未见其全貌。 作为顾问,你必须关注它&…...

限时活动|凭徽章领披萨大奖,玩转Moonbeam治理论坛
动动手指,无需每天打卡,用刷手机的零碎时间领一份Web3惊喜! 本次挑战的目标是鼓励大家参与社区治理、熟悉论坛操作。有关参与方式和原因的信息在Twitter上共享:有兴趣可以和ThinkWildCrypto一起探索论坛以解锁其功能、了解最近和正…...

Golang中struct{}和struct{}{}的区别你知道吗?
首先说下Golang中的结构体,结构体是由一系列具有相同类型或不同类型的数据构成的数据集合,Golang中使用关键字struct来创建一个结构体,语法如下:typeStudentstruct { Name string }下面定义一个Student结构体,例如&am…...
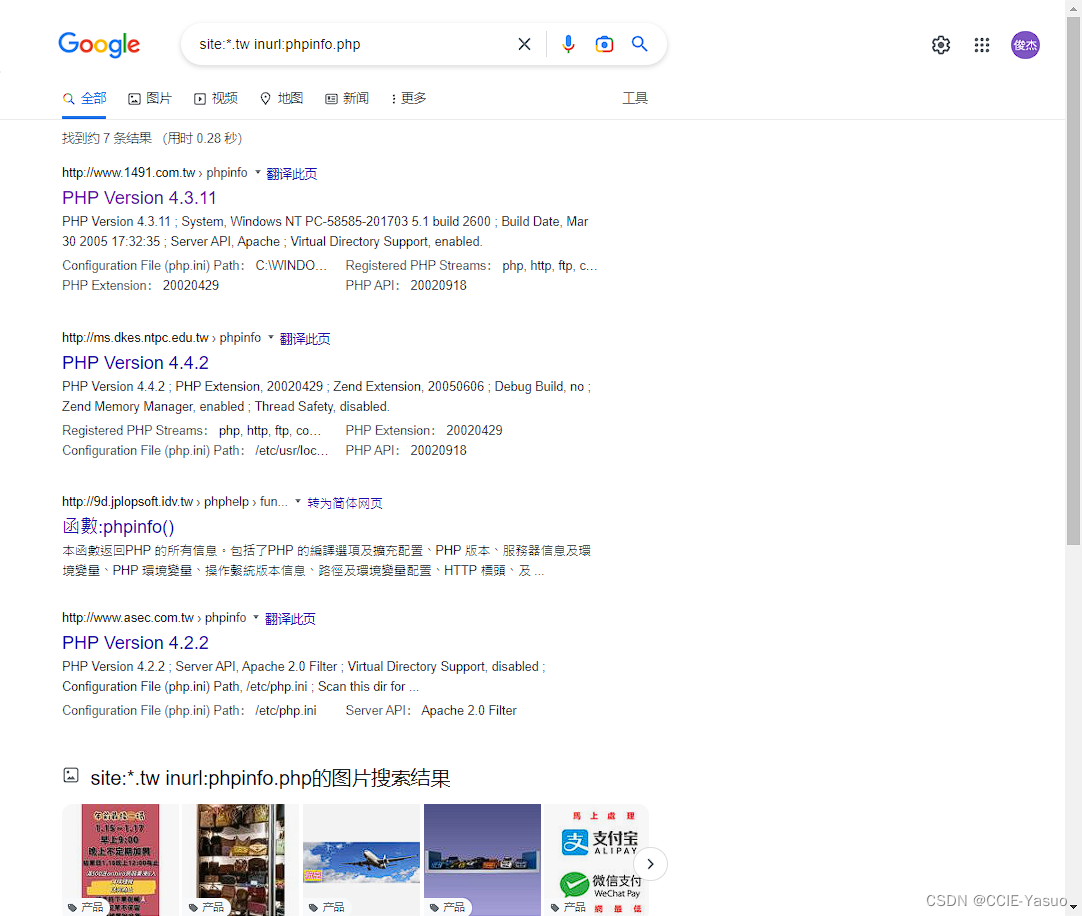
网络安全-信息收集- 谷歌浏览器插件收集信息,谷歌hacking搜索语法-带你玩不一样的搜索引擎
网络安全-信息收集- 谷歌浏览器插件收集信息,谷歌hacking搜索语法-带你玩不一样的搜索引擎 前言 一,我也是初学者记录的笔记 二,可能有错误的地方,请谨慎 三,欢迎各路大神指教 四,任何文章仅作为学习使用 …...

基础篇—一文掌握css的边框属性
CSS 边框属性 CSS边框属性允许你指定一个元素边框的样式和颜色。 1、边框样式 边框样式属性指定要显示什么样的边界。 border-style属性用来定义边框的样式 2、边框宽度 您可以通过 border-width 属性为边框指定宽度。 为边框指定宽度有两种方法:可以指定长度值,比如 2px…...
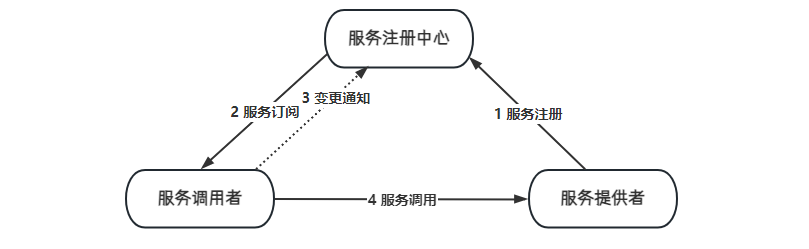
05服务发现:引入etcd服务注册中心
在分布式微服务架构中,服务注册发现组件(通常称为服务注册中心)往往有着举足轻重的作用,它的性能与稳定可能会直接影响到整个服务的状态,比如Spring Cloud中的Eureka、Dubbo中的Zookeeper等等,接下来我们就gRPC微服务中最常见的服务注册中心etcd,来讲述下两者在具体是怎…...

Pdfium.Net SDK 4.78.2704 完美Crack/Ptach
不限制时,/不限PDF体积、、、、、// version: 4.78.2704 | file size: 52.7 Mb Pdfium .Net SDK C# PDF 库 从头开始或从一堆扫描图像创建 PDF 编辑、合并、拆分和操作 PDF,提取文本和图像 嵌入独立的 Winforms 或 WPF PDF 查看器 支持:.Net…...
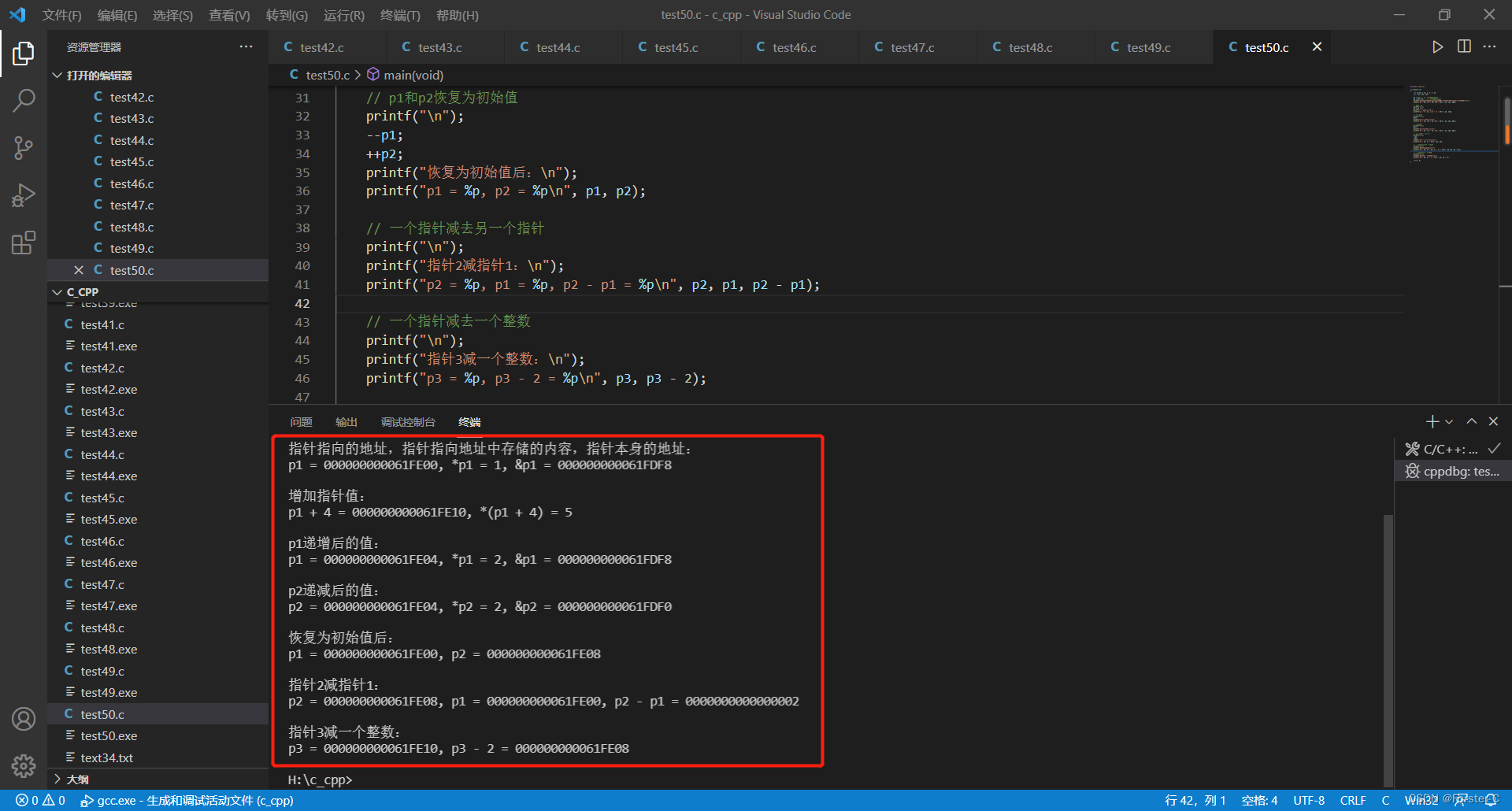
再学C语言38:指针操作
C提供了6种基本的指针操作 示例代码: #include <stdio.h>int main(void) {int arr[5] {1, 2, 3, 4, 5};int * p1, *p2, *p3;p1 arr; // 把一个地址赋给指针p2 &arr[2]; // 把一个地址赋给指针printf("指针指向的地址,指针指向地址中…...
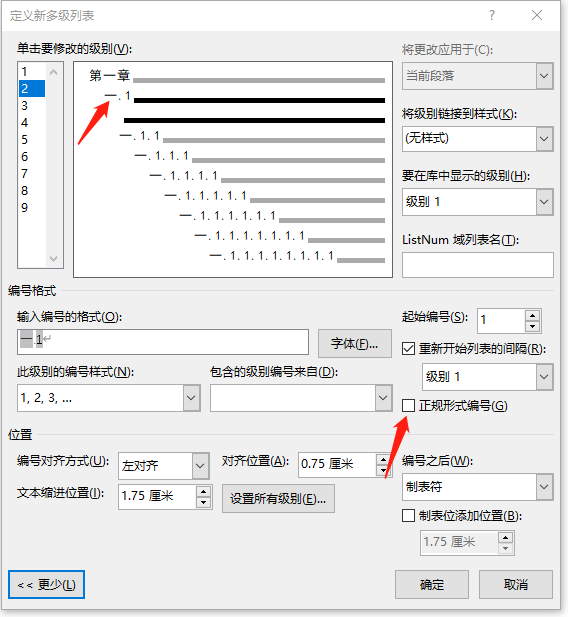
【论文Word排版】使用多级列表设置论文序号
在Word中对论文进行排版 1.设置章节前面的序号 1.1 需求 通常情况下要求如下 一级标题“第一章 XXX”,然后是“1.1 研究意义”, “1.2 研究现状” 之前的处理方式都是手打,并没有借助word的多级列表实现。这次趁着写毕业论文研究了一下。…...
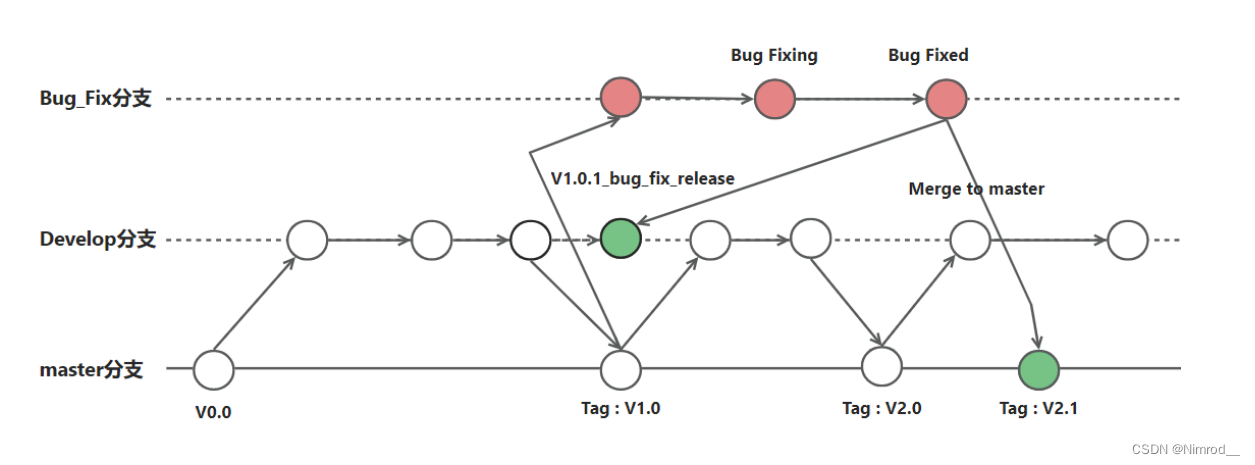
分支管理方案
背景 在工作的过程中,git管理方式已经成为每一个项目开发的基础,每个项目的开发都离不开git管理方式。 但是在使用的过程中,由于对git分支管理方案的了解不深,导致会出现分支管理不明确的情况。 本文主要是做科普作用ÿ…...
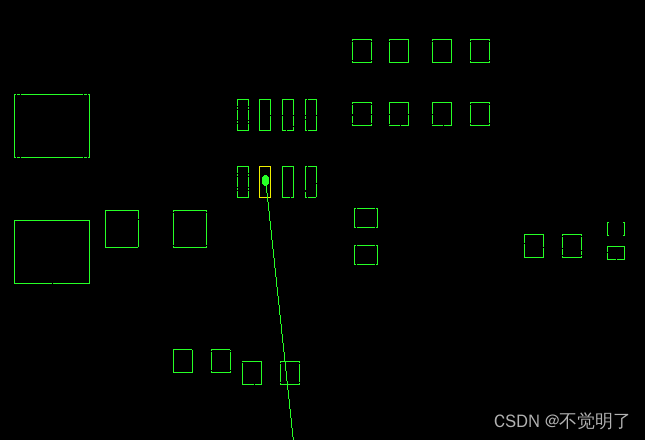
Allegro走线时如何自动关闭其它网络飞线显示操作指导
Allegro走线时如何自动关闭其它网络飞线显示操作指导 在做PCB设计的时候,尤其是在评估布线的时候,走某一个网络的时候,希望其它网络的飞线会被自动关闭,方便评估。 Allegro支持这个功能,如下图 走线前 走线后 具体操作如下 点击Route...

Linux中常用命令汇总二
Linux中常用命令汇总一文章地址:https://blog.csdn.net/u011837804/article/details/1289952531、时间日期类基本语法date [OPTION]... [FORMAT]选项说明选项说明-d<时间字符串>显示指定的“时间字符串”表示的时间,而非当前时间-s<日期时间>…...
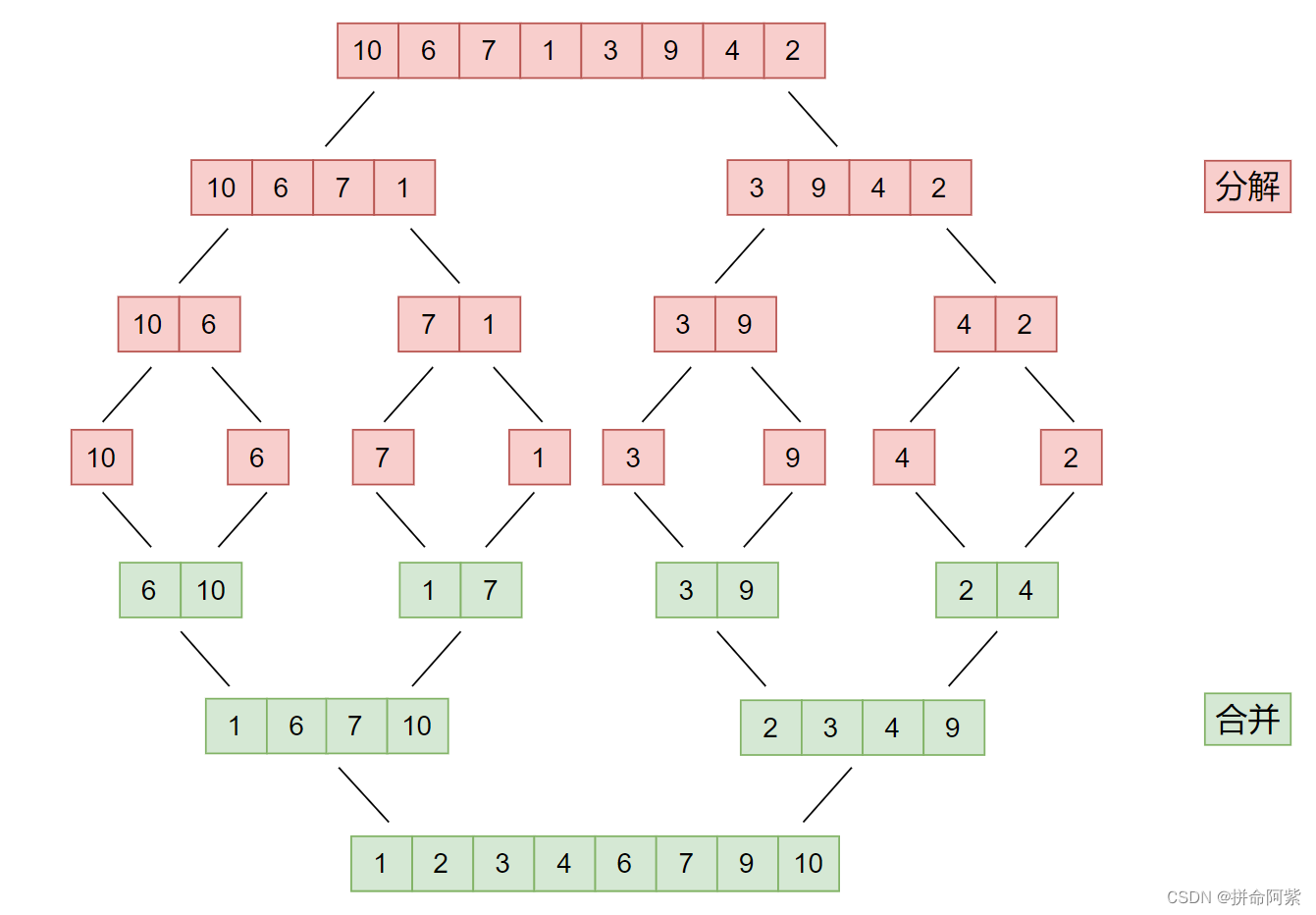
【数据结构】排序算法
目录 1.理解排序 1.1 排序的概念 1.2 排序的运用场景 1.3 常见的排序算法 2.插入排序算法 2.1 直接插入排序 2.2 希尔排序 3.选择排序算法 3.1 直接选择排序 3.2 堆排序 4.交换排序算法 4.1 冒泡排序 4.2 快速排序 4.2.1 hoare 法 4.2.2 挖坑法 4.2.3 前…...

[MySQL]初识数据库
哈喽,大家好!我是保护小周ღ,本期为大家带来的是 MySQL 数据库,也是新的知识,首先我们会初步认识什么是数据库,什么是Mysql 数据库,以及我们 mysql 主要学什么,SQL 语句简单使用&…...
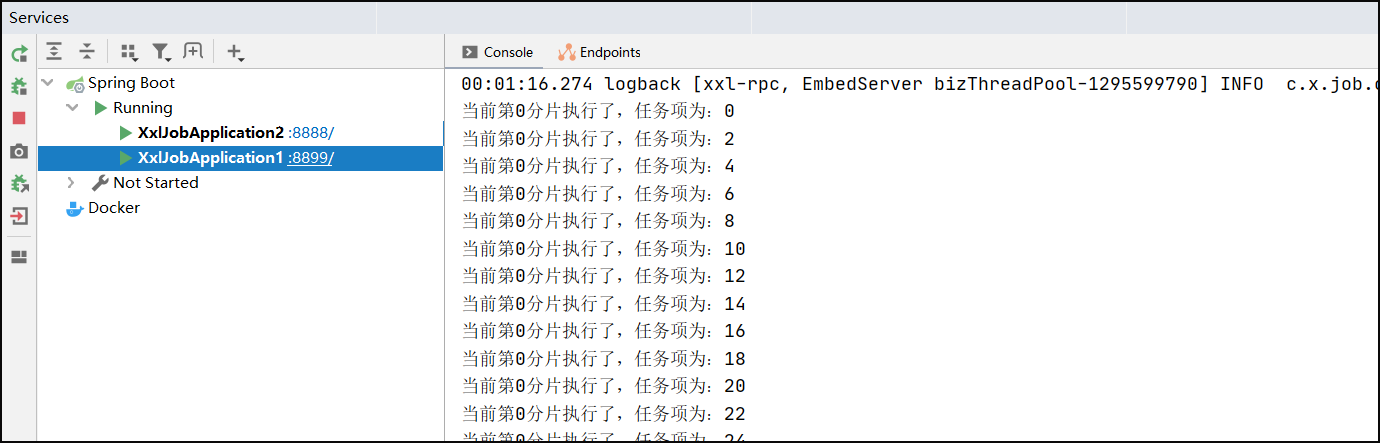
XXL-JOB分布式任务调度框架(二)-路由策略
文章目录1.引言2.任务详解2.1.执行器2.2.基础配置3.路由策略(第一个)-案例4.路由策略(最后一个)-案例5.轮询策略-案例7.分片广播任务1.引言 本篇文章承接上文《XXL-JOB分布式任务调度框架(一)-基础入门》,上一次和大家简单介绍了下 xxl-job 的由来以及使用方法&…...
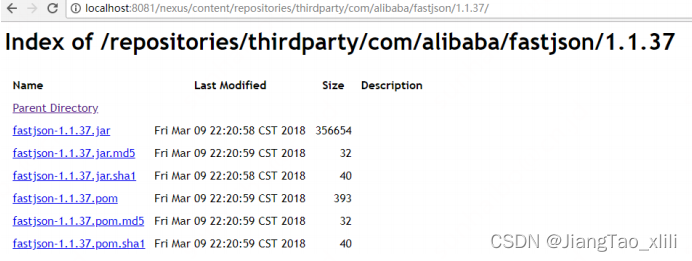
Java_Maven:5. 把第三方 jar 包放入本地仓库或私服
目录 1 导入本地库 2 导入私服 3 参数说明 1 导入本地库 随便找一个 jar 包测试,可以先 CMD进入到 jar 包所在位置,运行 mvn install:install-file -DgroupIdcom.alibaba -DartifactIdfastjson -Dversion1.1.37-Dfile fastjson-1.1.37.jar -Dpackaging…...
)
【剑指offer】03~05. 数组中的数字(C# 实现)
文章目录前言03. 数组中重复的数字04. 二维数组中的查找05. 替换空格结语前言 😃 大家好,我是writer桑,这是自己整理的 C# 做题记录,方便自己学习的同时分享出来,感谢支持。 03. 数组中重复的数字 题目描述࿱…...
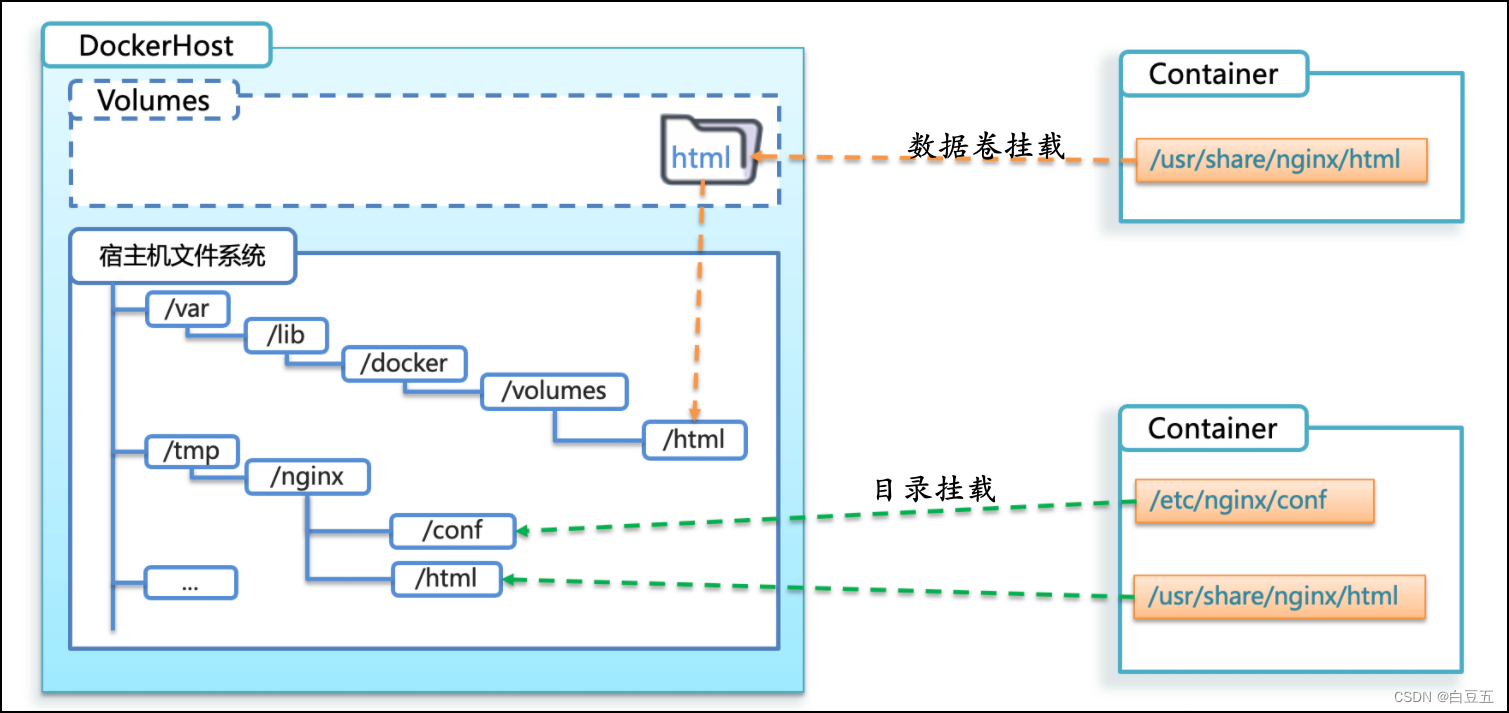
Docker入门教程
文章目录一、Docker概述1. 什么是容器技术?2. 什么是Docker3. 为什么要使用Docker4. Docker和虚拟机的对比5. Docker相关概念6. DockerHub7. Docker架构二、安装Docker1. 安装Docker2. 配置阿里云镜像加速三、Docker常用命令1. 帮助命令2. 镜像操作命令3. 容器操作命…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
