数据结构-栈队列链表树
1 栈
概念
- 栈是⼀个线性结构,在计算机中是⼀个相当常⻅的数据结构。
- 栈的特点是只能在某⼀端添加或删除数据,遵循先进后出的原则
实现
- 每种数据结构都可以⽤很多种⽅式来实现,其实可以把栈看成是数组的⼀个⼦集,所以这⾥使⽤数组来实现
class Stack {
constructor() {
this.stack = []
}
push(item) {
this.stack.push(item)
}
pop() {
this.stack.pop()
}
peek() {
return this.stack[this.getCount() - 1]
}
getCount() {
return this.stack.length
}
isEmpty() {
return this.getCount() === 0
}
}
应⽤
- 匹配括号,可以通过栈的特性来完成
var isValid = function (s) {
let map = {
'(': -1,
')': 1,
'[': -2,
']': 2,
'{': -3,
'}': 3
}
let stack = []
for (let i = 0; i < s.length; i++) {
if (map[s[i]] < 0) {
stack.push(s[i])
} else {
let last = stack.pop()
if (map[last] + map[s[i]] != 0) return false
}
}
if (stack.length > 0) return false
return true
};
2 队列
概念
- 队列⼀个线性结构,特点是在某⼀端添加数据,在另⼀端删除数据,遵循先进先出的原则
实现
- 这⾥会讲解两种实现队列的⽅式,分别是单链队列和循环队列
单链队列
class Queue {
constructor() {
this.queue = []
}
enQueue(item) {
this.queue.push(item)
}
deQueue() {
return this.queue.shift()
}
getHeader() {
return this.queue[0]
}
getLength() {
return this.queue.length
}
isEmpty() {
return this.getLength() === 0
}
}
- 因为单链队列在出队操作的时候需要 O(n) 的时间复杂度,所以引⼊了循环队列。循环队列的出队操作平均是 O(1) 的时间复杂度
循环队列
class SqQueue {
constructor(length) {
this.queue = new Array(length + 1)
// 队头
this.first = 0
// 队尾
this.last = 0// 当前队列⼤⼩
this.size = 0
}
enQueue(item) {
// 判断队尾 + 1 是否为队头
// 如果是就代表需要扩容数组
// % this.queue.length 是为了防⽌数组越界
if (this.first === (this.last + 1) % this.queue.length) {
this.resize(this.getLength() * 2 + 1)
}
this.queue[this.last] = item
this.size++
this.last = (this.last + 1) % this.queue.length
}
deQueue() {
if (this.isEmpty()) {
throw Error('Queue is empty')
}
let r = this.queue[this.first]
this.queue[this.first] = null
this.first = (this.first + 1) % this.queue.length
this.size--
// 判断当前队列⼤⼩是否过⼩
// 为了保证不浪费空间,在队列空间等于总⻓度四分之⼀时
// 且不为 2 时缩⼩总⻓度为当前的⼀半
if (this.size === this.getLength() / 4 && this.getLength() / 2 !== 0) {
this.resize(this.getLength() / 2)
}
return r
}
getHeader() {
if (this.isEmpty()) {
throw Error('Queue is empty')
}
return this.queue[this.first]
}
getLength() {
return this.queue.length - 1
}
isEmpty() {
return this.first === this.last
}
resize(length) {
let q = new Array(length)
for (let i = 0; i < length; i++) {
q[i] = this.queue[(i + this.first) % this.queue.length]
}
this.queue = q
this.first = 0
this.last = this.size
}
}
3 链表
概念
- 链表是⼀个线性结构,同时也是⼀个天然的递归结构。链表结构可以充分利⽤ 计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销⽐较⼤
实现
单向链表
class Node {
constructor(v, next) {
this.value = v
this.next = next
}
}
class LinkList {
constructor() {
// 链表⻓度
this.size = 0
// 虚拟头部
this.dummyNode = new Node(null, null)
}
find(header, index, currentIndex) {
if (index === currentIndex) return header
return this.find(header.next, index, currentIndex + 1)
}
addNode(v, index) {
this.checkIndex(index)
// 当往链表末尾插⼊时,prev.next 为空
// 其他情况时,因为要插⼊节点,所以插⼊的节点
// 的 next 应该是 prev.next// 然后设置 prev.next 为插⼊的节点
let prev = this.find(this.dummyNode, index, 0)
prev.next = new Node(v, prev.next)
this.size++
return prev.next
}
insertNode(v, index) {
return this.addNode(v, index)
}
addToFirst(v) {
return this.addNode(v, 0)
}
addToLast(v) {
return this.addNode(v, this.size)
}
removeNode(index, isLast) {
this.checkIndex(index)
index = isLast ? index - 1 : index
let prev = this.find(this.dummyNode, index, 0)
let node = prev.next
prev.next = node.next
node.next = null
this.size--
return node
}
removeFirstNode() {
return this.removeNode(0)
}
removeLastNode() {
return this.removeNode(this.size, true)
}
checkIndex(index) {
if (index < 0 || index > this.size) throw Error('Index error')
}
getNode(index) {
this.checkIndex(index)
if (this.isEmpty()) return
return this.find(this.dummyNode, index, 0).next
}
isEmpty() {
return this.size === 0
}
getSize() {
return this.size
}
}
4 树
⼆叉树
- 树拥有很多种结构,⼆叉树是树中最常⽤的结构,同时也是⼀个天然的递归结构。
- ⼆叉树拥有⼀个根节点,每个节点⾄多拥有两个⼦节点,分别为:左节点和右节点。树的最底部节点称之为叶节点,当⼀颗树的叶数量数量为满时,该树可以称之为满⼆叉树
⼆分搜索树
- ⼆分搜索树也是⼆叉树,拥有⼆叉树的特性。但是区别在于⼆分搜索树每个节点的值都⽐他的左⼦树的值⼤,⽐右⼦树的值⼩
- 这种存储⽅式很适合于数据搜索。如下图所示,当需要查找 6 的时候,因为需要查找的值⽐根节点的值⼤,所以只需要在根节点的右⼦树上寻找,⼤⼤提⾼了搜索效率
实现
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
}
}
class BST {
constructor() {
this.root = null
this.size = 0
}
getSize() {
return this.size
}
isEmpty() {
return this.size === 0
}
addNode(v) {
this.root = this._addChild(this.root, v)
}
// 添加节点时,需要⽐较添加的节点值和当前
// 节点值的⼤⼩
_addChild(node, v) {
if (!node) {
this.size++
return new Node(v)
}
if (node.value > v) {
node.left = this._addChild(node.left, v)
} else if (node.value < v) {
node.right = this._addChild(node.right, v)
}
return node
}
}
- 以上是最基本的⼆分搜索树实现,接下来实现树的遍历。
- 对于树的遍历来说,有三种遍历⽅法,分别是先序遍历、中序遍历、后序遍历。三种遍历的区别在于何时访问节点。在遍历树的过程中,每个节点都会遍历三次,分别是遍历到⾃⼰,遍历左⼦树和遍历右⼦树。如果需要实现先序遍历,那么只需要第⼀次遍历到节点时进⾏操作即可
// 先序遍历可⽤于打印树的结构
// 先序遍历先访问根节点,然后访问左节点,最后访问右节点。
preTraversal() {
this._pre(this.root)
}
_pre(node) {
if (node) {
console.log(node.value)
this._pre(node.left)
this._pre(node.right)
}
}
// 中序遍历可⽤于排序
// 对于 BST 来说,中序遍历可以实现⼀次遍历就
// 得到有序的值
// 中序遍历表示先访问左节点,然后访问根节点,最后访问右节点。
midTraversal() {
this._mid(this.root)
}
_mid(node) {
if (node) {
this._mid(node.left)
console.log(node.value)
this._mid(node.right)
}
}
// 后序遍历可⽤于先操作⼦节点
// 再操作⽗节点的场景
// 后序遍历表示先访问左节点,然后访问右节点,最后访问根节点。
backTraversal() {
this._back(this.root)
}
_back(node) {
if (node) {
this._back(node.left)
this._back(node.right)
console.log(node.value)
}
}
- 以上的这⼏种遍历都可以称之为深度遍历,对应的还有种遍历叫做⼴度遍历,也就是⼀层层地遍历树。对于⼴度遍历来说,我们需要利⽤之前讲过的队列结构来完成
breadthTraversal() {
if (!this.root) return null
let q = new Queue()
// 将根节点⼊队
q.enQueue(this.root)
// 循环判断队列是否为空,为空
// 代表树遍历完毕
while (!q.isEmpty()) {
// 将队⾸出队,判断是否有左右⼦树
// 有的话,就先左后右⼊队
let n = q.deQueue()
console.log(n.value)
if (n.left) q.enQueue(n.left)
if (n.right) q.enQueue(n.right)
}
}
- 接下来先介绍如何在树中寻找最⼩值或最⼤数。因为⼆分搜索树的特性,所以最⼩值⼀定在根节点的最左边,最⼤值相反
getMin() {
return this._getMin(this.root).value
}
_getMin(node) {
if (!node.left) return node
return this._getMin(node.left)
}
getMax() {
return this._getMax(this.root).value
}
_getMax(node) {
if (!node.right) return node
return this._getMin(node.right)
}
- 向上取整和向下取整,这两个操作是相反的,所以代码也是类似的,这⾥只介绍如何向下取整。既然是向下取整,那么根据⼆分搜索树的特性,值⼀定在根节点的左侧。只需要⼀直遍历左⼦树直到当前节点的值不再⼤于等于需要的值,然后判断节点是否还拥有右⼦树。如果有的话,继续上⾯的递归判断
floor(v) {
let node = this._floor(this.root, v)
return node ? node.value : null
}
_floor(node, v) {
if (!node) return null
if (node.value === v) return v
// 如果当前节点值还⽐需要的值⼤,就继续递归
if (node.value > v) {
return this._floor(node.left, v)
}
// 判断当前节点是否拥有右⼦树
let right = this._floor(node.right, v)
if (right) return right
return node
}
- 排名,这是⽤于获取给定值的排名或者排名第⼏的节点的值,这两个操作也是相反的,所以这个只介绍如何获取排名第⼏的节点的值。对于这个操作⽽⾔,我们需要略微的改造点代码,让每个节点拥有⼀个 size 属性。该属性表示该节点下有多少⼦节点(包含⾃身)
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
// 修改代码
this.size = 1
}
}
// 新增代码
_getSize(node) {
return node ? node.size : 0
}
_addChild(node, v) {
if (!node) {
return new Node(v)
}
if (node.value > v) {
// 修改代码
node.size++
node.left = this._addChild(node.left, v)
} else if (node.value < v) {
// 修改代码
node.size++
node.right = this._addChild(node.right, v)
}
return node
}
select(k) {
let node = this._select(this.root, k)
return node ? node.value : null
}
_select(node, k) {
if (!node) return null
// 先获取左⼦树下有⼏个节点
let size = node.left ? node.left.size : 0
// 判断 size 是否⼤于 k
// 如果⼤于 k,代表所需要的节点在左节点
if (size > k) return this._select(node.left, k)
// 如果⼩于 k,代表所需要的节点在右节点
// 注意这⾥需要重新计算 k,减去根节点除了右⼦树的节点数量
if (size < k) return this._select(node.right, k - size - 1)
return node
}
- 接下来讲解的是⼆分搜索树中最难实现的部分:删除节点。因为对于删除节点来说,会存在以下⼏种情况
- 需要删除的节点没有⼦树
- 需要删除的节点只有⼀条⼦树
- 需要删除的节点有左右两条树
- 对于前两种情况很好解决,但是第三种情况就有难度了,所以先来实现相对简单的操作:删除最⼩节点,对于删除最⼩节点来说,是不存在第三种情况的,删除最⼤节点操作是和删除最⼩节点相反的,所以这⾥也就不再赘述
delectMin() {
this.root = this._delectMin(this.root)
console.log(this.root)
}
_delectMin(node) {
// ⼀直递归左⼦树
// 如果左⼦树为空,就判断节点是否拥有右⼦树
// 有右⼦树的话就把需要删除的节点替换为右⼦树
if ((node != null) & !node.left) return node.right
node.left = this._delectMin(node.left)
// 最后需要重新维护下节点的 `size`
node.size = this._getSize(node.left) + this._getSize(node.right) + 1
return node
}
delect(v) {
this.root = this._delect(this.root, v)
}
- 最后讲解的就是如何删除任意节点了。对于这个操作, T.Hibbard 在 1962 年提出了解决这个难题的办法,也就是如何解决第三种情况。
- 当遇到这种情况时,需要取出当前节点的后继节点(也就是当前节点右⼦树的最⼩节点)来替换需要删除的节点。然后将需要删除节点的左⼦树赋值给后继结点,右⼦树删除后继结点后赋值给他。
- 你如果对于这个解决办法有疑问的话,可以这样考虑。因为⼆分搜索树的特性,⽗节点⼀定⽐所有左⼦节点⼤,⽐所有右⼦节点⼩。那么当需要删除⽗节点时,势必需要拿出⼀个⽐⽗节点⼤的节点来替换⽗节点。这个节点肯定不存在于左⼦树,必然存在于右⼦树。然后⼜需要保持⽗节点都是⽐右⼦节点⼩的,那么就可以取出右⼦树中最⼩的那个节点来替换⽗节点
_delect(node, v) {
if (!node) return null
// 寻找的节点⽐当前节点⼩,去左⼦树找
if (node.value < v) {
node.right = this._delect(node.right, v)
} else if (node.value > v) {
// 寻找的节点⽐当前节点⼤,去右⼦树找
node.left = this._delect(node.left, v)
} else {
// 进⼊这个条件说明已经找到节点
// 先判断节点是否拥有拥有左右⼦树中的⼀个
// 是的话,将⼦树返回出去,这⾥和 `_delectMin` 的操作⼀样
if (!node.left) return node.right
if (!node.right) return node.left
// 进⼊这⾥,代表节点拥有左右⼦树
// 先取出当前节点的后继结点,也就是取当前节点右⼦树的最⼩值
let min = this._getMin(node.right)
// 取出最⼩值后,删除最⼩值
// 然后把删除节点后的⼦树赋值给最⼩值节点
min.right = this._delectMin(node.right)
// 左⼦树不动
min.left = node.left
node = min
}
// 维护 size
node.size = this._getSize(node.left) + this._getSize(node.right) + 1
return node
}
相关文章:

数据结构-栈队列链表树
1 栈 概念 栈是⼀个线性结构,在计算机中是⼀个相当常⻅的数据结构。栈的特点是只能在某⼀端添加或删除数据,遵循先进后出的原则 实现 每种数据结构都可以⽤很多种⽅式来实现,其实可以把栈看成是数组的⼀个⼦集,所以这⾥使⽤数…...

clickhouse功能使用
离线聚合 物化视图 clickhouse需在AggregatingMergeTree之上建立物化视图来完成聚合的效果。以小时聚合为例说明 首先创建表,此处是本地表,且没有副本 #创建表 CREATE TABLE datasets.bt_stats (`btname` String,`record` UInt64,`EventTime` DateTime...
java中使用Jsoup和Itext实现将html转换为PDF
1.在build.gradle中安装所需依赖: implementation group: com.itextpdf, name: itextpdf, version: 5.5.13 implementation group: com.itextpdf.tool, name: xmlworker, version: 5.5.13 implementation group: org.jsoup, name: jsoup, version: 1.15.32.创建工具…...

无人驾驶实战-第七课(高精地图和V2X )
高精地图是无人驾驶中的重要一环,对环境感知、规划与定位等都有重要的作用。 高精地图的特点: 可视化、静态目标、地图信息、点云数据 高精地图与导航地图的区别 High Definition Map Navigation Map Precision cm m Information 3D lane info Mo…...

springboot集成Sentinel
1、添加依赖 该版本匹配springboot 2.3.x和2.4.x <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-starter-alibaba-sentinel</artifactId><version>2021.1</version> </dependency> 2、Sentin…...

数据结构——单链表OJ题
单链表OJ题 前言一、删除链表中等于给定值 val 的所有节点二、反转一个单链表三、返回链表的中间结点四、输出该链表中倒数第k个结点五、将两个有序链表合并六、链表的回文结构七、将链表分割成两部分八、找出第一个公共结点九、判断链表中是否有环总结 前言 在前面的博客中我…...

【雕爷学编程】MicroPython动手做(31)——物联网之Easy IoT
1、物联网的诞生 美国计算机巨头微软(Microsoft)创办人、世界首富比尔盖茨,在1995年出版的《未来之路》一书中,提及“物物互联”。1998年麻省理工学院提出,当时被称作EPC系统的物联网构想。2005年11月,国际电信联盟发布《ITU互联网…...

《前端开发 实践之 构建工具的了解》
目录 构建工具的了解Vite 构建工具了解基本使用 构建工具的了解 前端构建工具之一:vite Vite 构建工具了解 todo 基本使用 todo...

MySQL 主从搭建
文章目录 前言一、MySQL 主从是什么?二、通过 Docker 部署三、配置主从关系四、实际情况分析&解决方案五、常见问题处理1、CLONE需要版本不同2、CLONE需要参数相同 总结 前言 MySQL 主从搭建 操作系统:CentOS Linux release 7.9.2009 (Core) 操作系…...
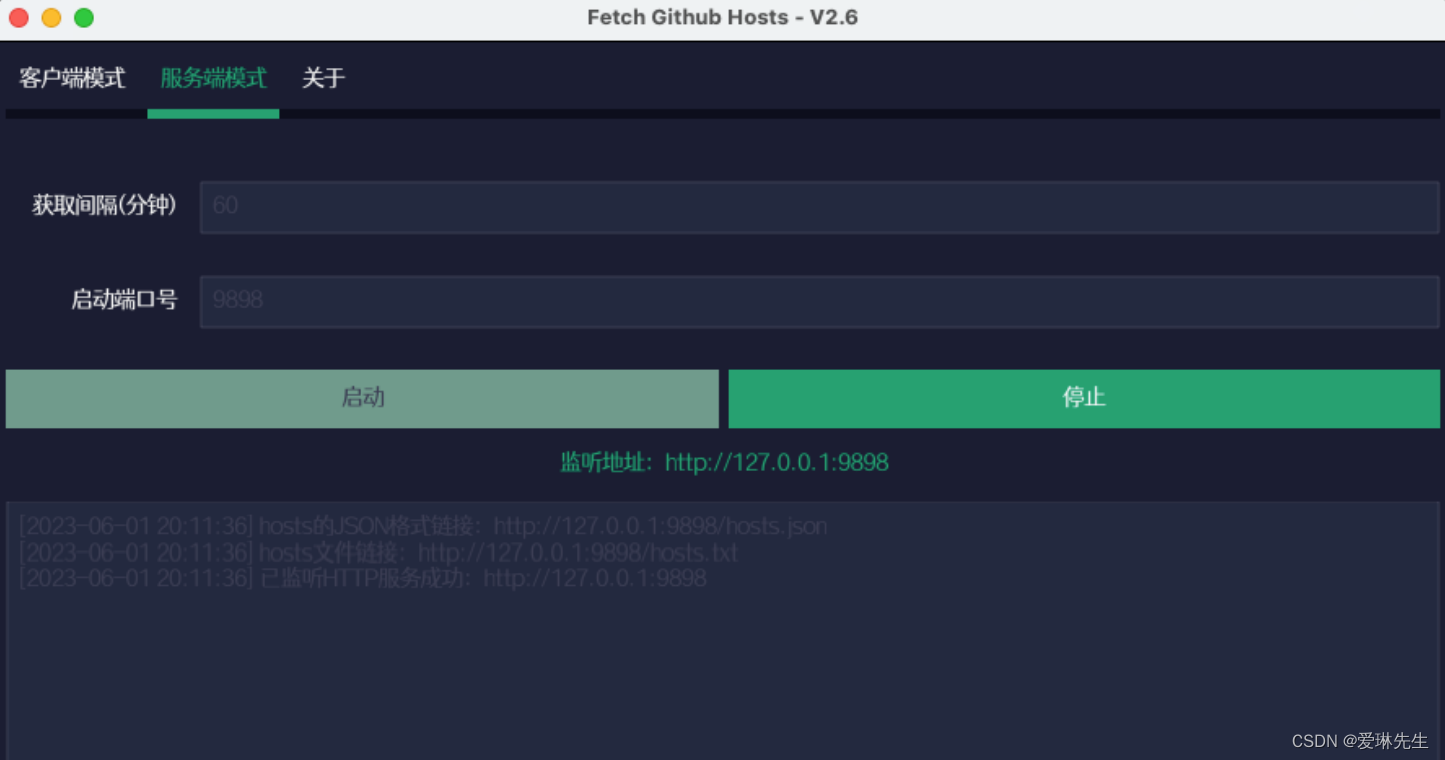
国内GitHub加速访问工具-Fetch GitHub Hosts
一、工具介绍 Fetch GitHub Hosts是一款开源跨平台的国内GitHub加速访问工具,主要为解决研究及学习人员访问 Github 过慢或其他问题而提供的 Github Hosts 同步工具。 项目原理:是通过部署此项目本身的服务器来获取 github.com 的 hosts,而…...
Webpack5新手入门简单配置
1.初始化项目 yarn init -y 2.安装依赖 yarn add -D webpack5.75.0 webpack-cli5.0.0 3.新建index.js 说明:写入下面的一句话 console.log("hello webpack"); 4.执行命令 说明:如果没有安装webpack脚手架就不能执行yarn webpack(…...

基于ali-oss实现不同类型文件上传不同的bucket
基于ali-oss实现不同类型文件上传不同的bucket,并根据大小选择直接上传还是分片上传 1 配置OSS2 引入依赖3 上传核心代码4 文件回显 1 配置OSS 可以看阿里云文档 ps:记得配置跨域 2 引入依赖 pnpm install ali-oss -save3 上传核心代码 import OSS from "ali-oss"…...

域名校验?反爬界的掩耳盗铃!
这一集我们讲一个比较简单的域名校验,可能你没有听过这个名字,因为这个名字是我编的,那么它究竟是什么呢?又为什么说它是掩耳盗铃呢?我们来看看下面的案例: 必应搜索页隐藏内容虎嗅新闻跳转404 import re…...
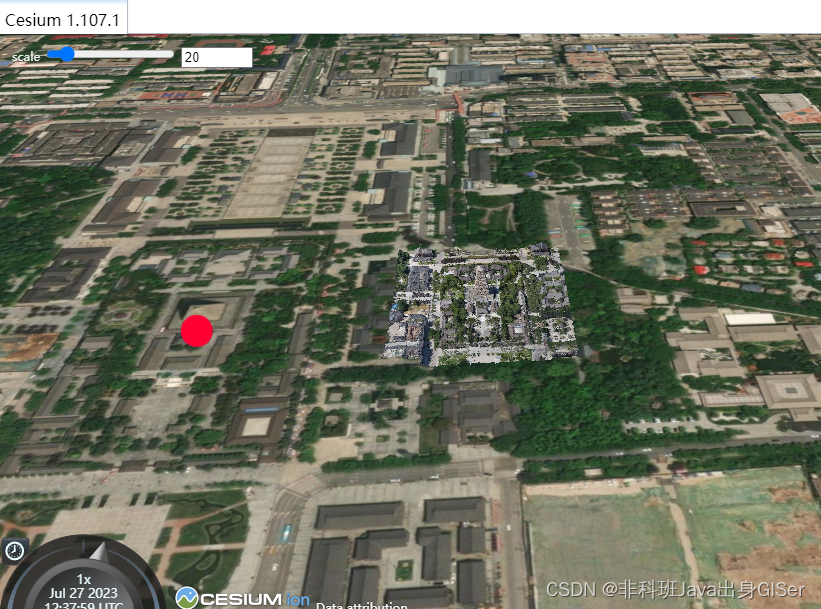
Cesium 实战教程 - 调整 3dtiles 倾斜摄影大小
Cesium 实战教程 - 调整 3dtiles 倾斜摄影大小 核心代码完整代码在线示例 之前由于误解遇到一个特殊的需求:想要把三维球上叠加倾斜摄影进行自由放大缩小,跟随地图的缩放进行缩放。 后来经过搜索、尝试,终于实现了需求。 但是,后…...
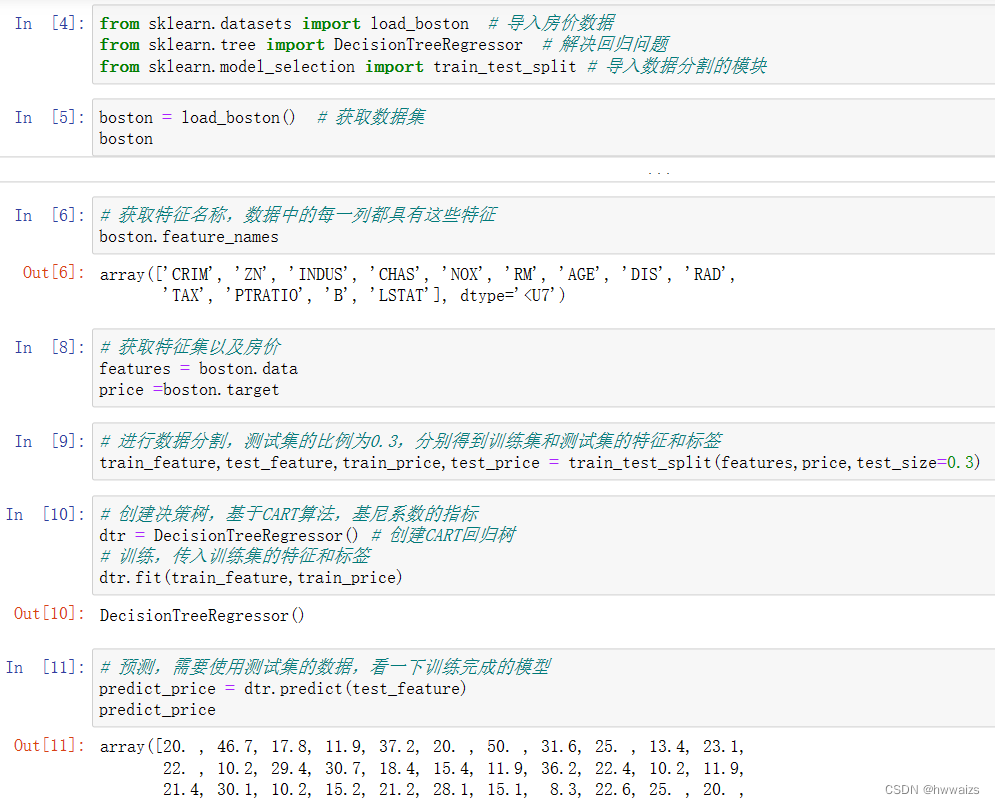
python机器学习(七)决策树(下) 特征工程、字典特征、文本特征、决策树算法API、可视化、解决回归问题
决策树算法 特征工程-特征提取 特征提取就是将任意数据转换为可用于机器学习的数字特征。计算机无法直接识别字符串,将字符串转换为机器可以读懂的数字特征,才能让计算机理解该字符串(特征)表达的意义。 主要分为:字典特征提取(特征离散化)…...
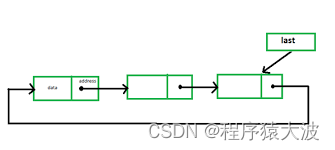
数据结构与算法中的双向链表
链表概念在现实世界中使用得很普遍。当我们使用 Spotify 播放队列中的下一首歌曲时,我们学到的单链表的概念就开始发挥作用。但是要播放队列中的上一首歌曲到底可以做什么呢? 在这篇博客中,我们将了解与数据结构相关的另一个概念,…...
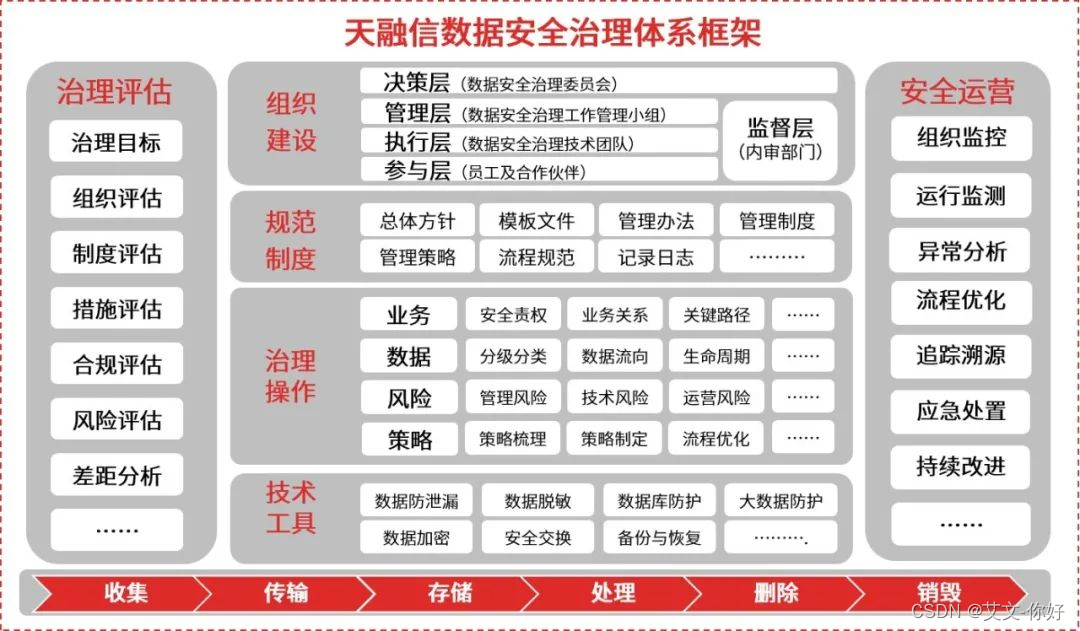
数据安全治理的关键-数据分类分级工具
强大的资产发现能力 多种资产发现方式的组合应用,能够最大程度地提高资产发现能力。 灵活的敏感数据分类分级规则 内置丰富的敏感数据分类分级规则,支持正则表达式、关键词组、非结构化指纹、结构化指纹、机器聚类等多种匹配方式,并且规则…...
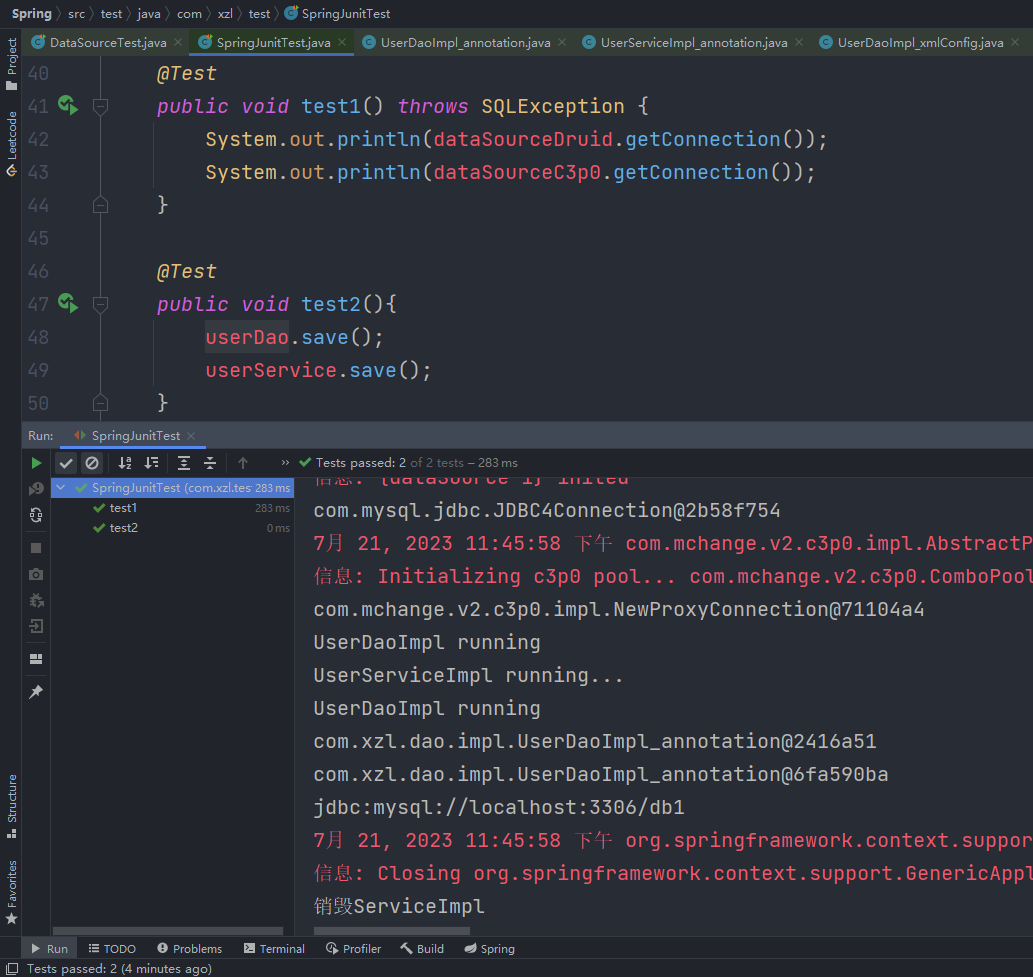
Spring集成Junit
目录 1、简介 2、Junit存在的问题 3、回顾Junit注解 4、集成步骤 4.1、导入坐标 4.2、Runwith 4.3、ContextConfiguration 4.4、Autowired 4.5、Test 4.6、代码 5、补充说明 5.1、Runwith 5.2、BlockJUnit4ClassRunner 5.3、没有配置Runwith ⭐作者介绍࿱…...
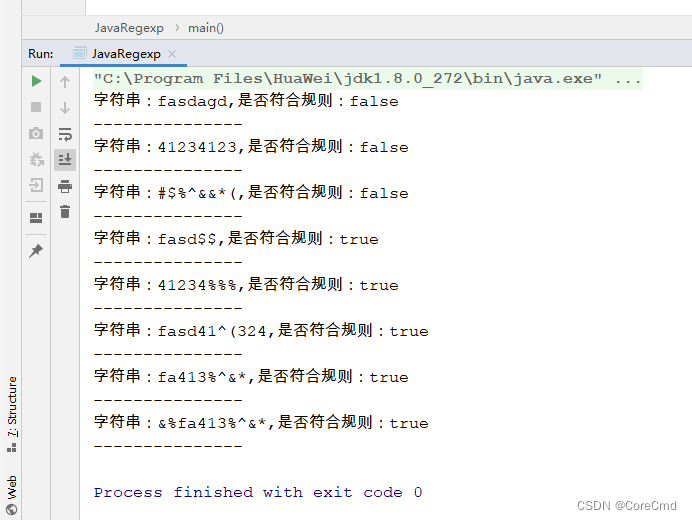
Java正则校验密码至少包含:字母数字特殊符号中的2种
一、语法 字符说明\将下一字符标记为特殊字符、文本、反向引用或八进制转义符。例如, n匹配字符 n。\n 匹配换行符。序列 \\\\ 匹配 \\ ,\\( 匹配 (。^匹配输入字符串开始的位置。如果设置了 RegExp 对象的 Multiline 属性,^ 还会与"\n…...
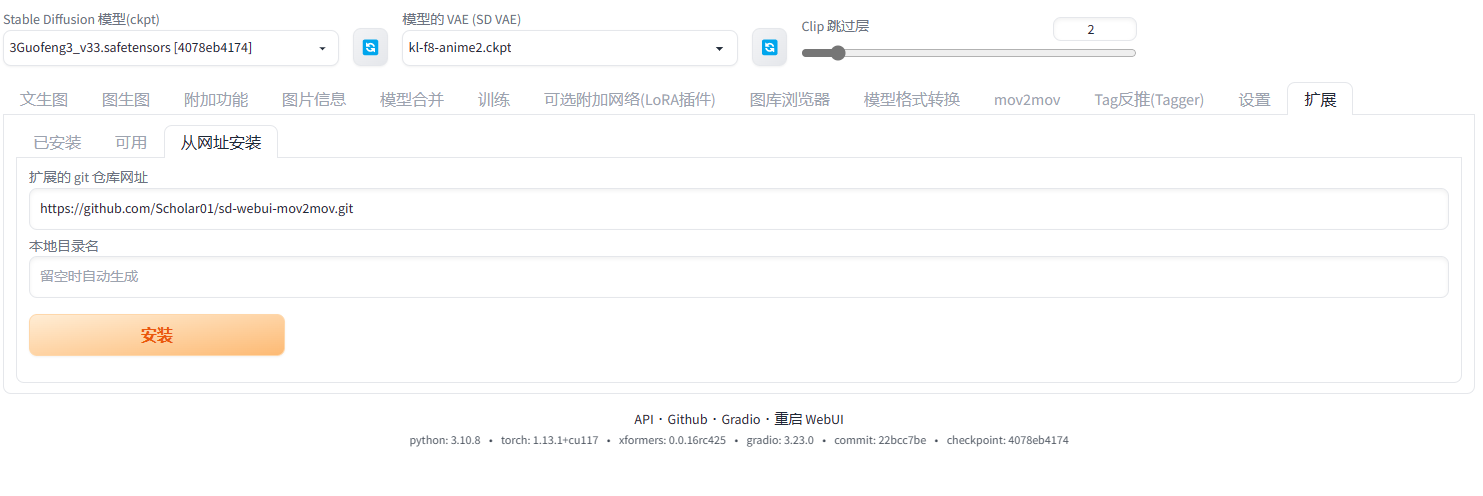
Stable Diffusion教程(6) - 扩展安装
打开stable diffusion webUI界面 加载插件列表 依次点击扩展->可用->加载自 搜索插件 首先在搜索框输入你要安装的插件,然后点击插件后面的安装按钮 如果你需要的插件这里面没有找到,可通过通网址安装的方式安装。 在git仓库网址输入框输入的你插件…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
