深度学习笔记-暂退法(Drop out)
背景
在机器学习的模型中,如果模型的参数太多,而训练样本又太少,训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题,过拟合具体表现在:模型在训练数据上损失函数较小,预测准确率较高;但是在测试数据上损失函数比较大,预测准确率较低。
过拟合是很多机器学习的通病。如果模型过拟合,那么得到的模型几乎不能用。为了解决过拟合问题,一般会采用模型集成的方法,即训练多个模型进行组合。此时,训练模型费时就成为一个很大的问题,不仅训练多个模型费时,测试多个模型也是很费时。
综上所述,训练深度神经网络的时候,总是会遇到两大缺点:
(1)容易过拟合
(2)费时
Dropout可以比较有效的缓解过拟合的发生,在一定程度上达到正则化的效果。
小结
- 好的模型应该是简单的模型,能防止过拟合。 简单性的另一个角度是平滑性,即函数不应该对其输入的微小变化敏感。
- 加入噪声能在输入-输出映射上增强平滑性。
- 在暂退法(Drop out )中增加噪声的方式是:在前向传播过程中,计算每一内部层的同时注入噪声。将概率p的值置为0, 其他值修改为 h/(1-p),保证期望前后不变。

- 实践中的暂退法为:

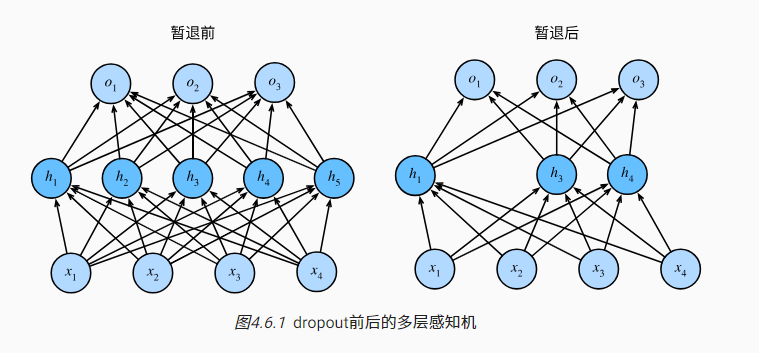
5. 在测试时不用使用dropout. 我们在测试时不用暂退法。 给定一个训练好的模型和一个新的样本,我们不会丢弃任何节点,因此不需要标准化
6. 实现:
dropout1, dropout2 = 0.2, 0.5
net = nn.Sequential(nn.Flatten(),nn.Linear(784, 256),nn.ReLU(),# 在第一个全连接层之后添加一个dropout层nn.Dropout(dropout1),nn.Linear(256, 256),nn.ReLU(),# 在第二个全连接层之后添加一个dropout层nn.Dropout(dropout2),nn.Linear(256, 10))def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, std=0.01)net.apply(init_weights);
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
相关文章:

深度学习笔记-暂退法(Drop out)
背景 在机器学习的模型中,如果模型的参数太多,而训练样本又太少,训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题,过拟合具体表现在:模型在训练数据上损失函数较小,预…...

使用自适应去噪在线顺序极限学习机预测飞机发动机剩余使用寿命(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
实验5-7 使用函数求1到10的阶乘和 (10 分)
实验5-7 使用函数求1到10的阶乘和 (10 分) 本题要求实现一个计算非负整数阶乘的简单函数,使得可以利用该函数,计算1!2!⋯10!的值。 函数接口定义: double fact( int n ); 其中n是用户传入的参数,其值不超过…...
kafka部署
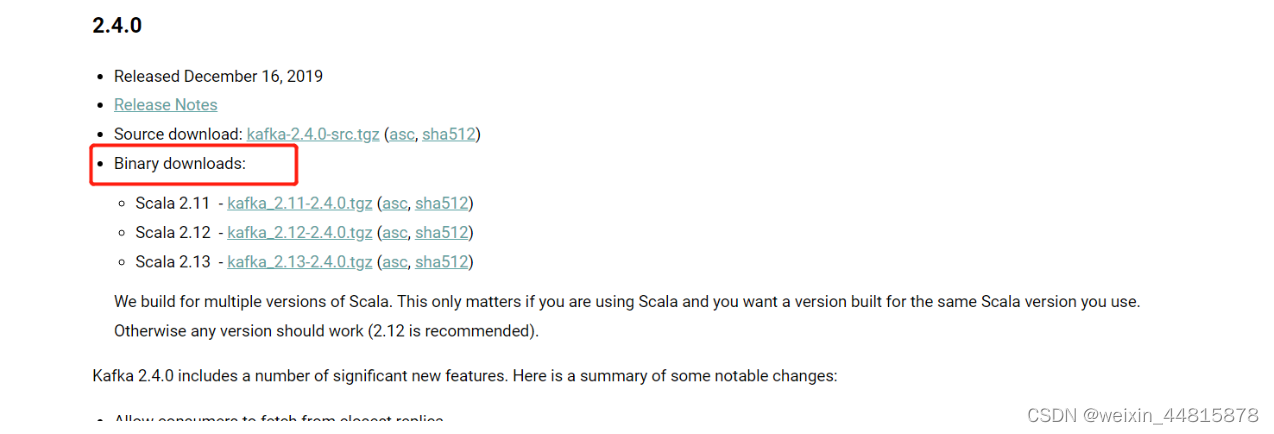
1.kafka安装部署 1.1 kafaka下载 https://archive.apache.org/dist/kafka/2.4.0/kafka_2.12-2.4.0.tgz Binary downloads是指预编译的软件包,可供直接下载和安装,无需手动编译。在计算机领域中,二进制下载通常指预构建的软件分发包,可以直接安装在系统上并使用 "2.…...

Spring Security6入门及自定义登录
一、前言 Spring Security已经更新到了6.x,通过本专栏记录以下Spring Security6学习过程,当然大家可参考Spring Security5专栏对比学习 Spring Security5专栏地址:security5 Spring Security是spring家族产品中的一个安全框架,核心功能包括…...

开放式蓝牙耳机哪个品牌好用?盘点几款很不错的开放式耳机
相比传统入耳式耳机,开放式耳机因其不入耳不伤耳的开放设计,不仅带来了舒适的佩戴体验,还创造了一种与周围环境互动的全新方式,户外运动过程时也无需担心发生事故,安全性更高。我整理了几款比较好用的开放式耳机给大…...
WebGL: 几个入门小例子
本文罗列几个WebGL入门例子,用于帮助WebGL学习。 一、概述 WebGL (Web Graphics Library)是一组基于Open ES、在Web内渲染3D图形的Javascript APIs。 Ref. from Khronos Group: WebGL WebGL™ is a cross-platform, royalty-free open web standard for a low-lev…...
刷题指南 —— 第一弹)
PAT(Advanced Level)刷题指南 —— 第一弹
一、1001 A+B Format 1. 问题重述 给两个整数,输出这两个数的加和的结果,每三位用逗号分隔。 2. Sample Input -1000000 93. Sample Output -999,9914. 题解 思路:直接将两个整数相加,判断是否为负,是负数则直接输出负号并转为正数;然后将正数转为字符串,按规则每…...
)
【BASH】回顾与知识点梳理(九)
【BASH】回顾与知识点梳理 九 九. 扩展正则表达式(延伸正规表示法)9.1 egrep命令语法匹配指定模式的行(用法和grep相同)忽略大小写匹配(用法和grep相同)反向匹配(用法和grep相同)显示行号(用法和grep相同)递归搜索目录(用法和grep相同)匹配整词(用法和grep相同)统计匹配行数(用…...
Android 版本 对应的 API版本
Android 14(开发者预览版) 如需详细了解平台变更,请参阅 Android 14 文档。 Android 13(API 级别 33) 如需详细了解平台变更,请参阅 Android 13 文档。 Android 12(API 级别 31、32…...

Django 异常信息 E302 expected 2 blank lines, found 1
在Django中,PEP 8风格指南建议在任何类定义之前都应该有两个空白行,包括视图(views)。错误信息"E302 expected 2 blank lines, found 1"表示在类定义之前只有一个空白行,而Django希望有两个空白行。 要修复…...

2019年09月《全国青少年软件编程等级考试》Python一级真题解析
一、单选题 第1题 关于Python的编程环境,下列的哪个表述是正确的? A:Python的编程环境是图形化的; B:Python只有一种编程环境ipython; C:Python自带的编程环境是IDLE; D&#…...

mybatis如何防止SQL注入
阅读正文: mybatis是如何防止SQL注入的 1、首先看一下下面两个sql语句的区别: <select id"selectByNameAndPassword" parameterType"java.util.Map" resultMap"BaseResultMap"> select id, usernam…...
DoIP学习笔记系列:(三)用CAPL脚本过“安全认证”,$27服务实现
文章目录 1. 如何调用接口通过安全认证?如何新建CAPL工程,在此不再赘述,本章主要分享一下如何在CAPL中调用DoIP接口、diag接口进行DoIP和诊断的测试。 注意:CANoe工具本身的使用没什么难的,所谓会者不难难者不会,各位小伙伴有疑问要多问,多交流,往往难事都只是一层窗户…...

【Linux】多路转接 -- select函数
文章目录 1. 认识select函数2. select函数原型3. socket就绪条件4. select工作流程5. select服务器6. select的优缺点 首先我们要了解一下,什么是多路转接? 多路转接也叫多路复用,是一种用于管理多个IO通道的技术。它能实现同时监听和处理多个…...

ospf于mgre中应用(直连与星型拓扑)
题目 地址配置 R1: R2: R3: R4: R5: ISP: R1/2/3的星型拓扑结构 R1配置: interface Tunnel0/0/0 ip address 192.168.6.1 255.255.255.0 tunnel-protocol gre p2mp source 200.1.1.1 ospf …...
Web压测工具http_load原理分析
01、前言 http_load是一款测试web服务器性能的开源工具,从下面的网址可以下载到最新版本的http_load: http://www.acme.com/software/http_load/ 这个软件一直在保持着更新(不像webbench,已经是十年的老古董了。 webbench的源…...

flask------消息闪现 flash
1介绍 flask提供了一个非常有用的flash()函数,它可以用来“闪现”需要提示给用户的消息,比如当用户登录成功后显示“欢迎回来!”。在视图函数调用flash()函数,传入消息内容,flash()函数把消息存…...

【C++】数据结构与算法:常用查找算法
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍常用查找算法。 学其所用,用其所学。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下次更新不迷路…...
【Spring Cloud 六】Hystrix熔断
这里写目录标题 系列文章目录背景一、Hystrix是什么服务雪崩服务容错的相关概念熔断器降级超时控制限流 二、会什么要有Hystrix三、如何使用Hystrix进行熔断处理整体项目代码服务提供者pom文件yml配置文件启动类controller 服务消费者pom文件yml配置文件启动类feignhystrixcont…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
