二叉树的性质、前中后序遍历【详细】
- 1. 树概念
- 2.二叉树的概念
- 1.2二叉树的性质
- 3.二叉树遍历
- 3.2前序遍历
- 3.2 中序遍历
- 3.3 后序遍历
1. 树概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合,有二叉树,N叉树等等。
- 子树是互不相交的(比如B不能连接C,D不能连接E)
- 除了根节点外,每个节点有且只有一个父节点。(A是B、C、D、E的父节点,B是F、G的父节点)
- 一颗有N个节点的树,有N-1条边。 (下图有10个节点,9条边)
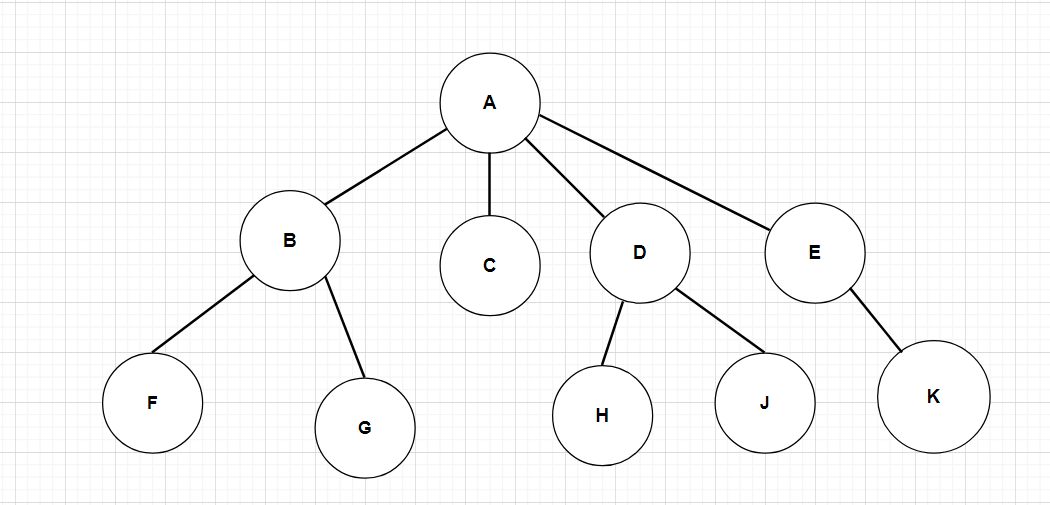
在树结构中,度是指一个节点的子节点个数的最大值。如果一个节点没有子节点,则其度为0;如果一个节点只有一个子节点,则其度为1;如果一个节点有两个子节点,则其度为2,以此类推。【二叉树不存在度大于2的节点,上图是个N叉树】
- 结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为4,B的度为2,F的度为0
- 树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为4
- 叶子结点或终端结点:度为0的结点称为叶结点; 如上图:C、F、G、H、等节点为叶结点
- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点,B是F的父节点,同样也是G的父节点。
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点,C是A的孩子节点…
- 根结点:一棵树中,没有父结点的结点;如上图:A
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推。上图树的层次是3层
- 树的高度或深度:树中结点的最大层次; 如上图:树的高度为3
- 非终端结点或分支结点:度不为0的结点; 如上图:B、D、E…等节点为分支结点
- 兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点,共同的父节点是A
- 堂兄弟结点:在同一层的结点互为堂兄弟;如上图:G、H互为兄弟结点
- 结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先,B是F的祖先
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
- 森林:由m(m>=0)棵互不相交的树组成的集合称为森林
2.二叉树的概念
二叉树是一种树形结构,其中每个节点最多有两个子节点。 二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树。

-
二叉树有左右之分,次序不能颠倒,因此二叉树是有序树。如上图,从上到下,从左往右,依次为1、2、3、4、5、6。所谓有序是指从左往
-
. **满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。**也就是说,如果一棵 二叉树的层数为K,且结点总数是
2 k − 1 2^k-1 2k−1
,则它就是满二叉树。 -
完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n 个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完 全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

1.2二叉树的性质
-
若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)(i>0)个结点
-
若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是
2 k − 1 2^k-1 2k−1
(k>=0) -
对任何一棵二叉树, **如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1,**也就是叶子节点比非叶子节点多1个。

-
具有n个结点的完全二叉树的深度K为
l o g 2 ( n + 1 ) log2(n+1) log2(n+1)
上取整。- 根据第二点性质可以推导出,2^k -1= n --> 2^k = n+1,这个k就等于第4点中提到的k,因为k为log2(n+1);那么也就是求2的多少次方等于k,假设有9个节点,9+1 等于10,2的3次方等于8,2的4次方等于16,向上取整就是取4。该二叉树深度为4。
-
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i 的结点有:
- 若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点【知道孩子序号,求父节点】
- 若2i+1<N,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子。
3.二叉树遍历
二叉树的遍历是指从根节点出发,按照某种次序依次访问二叉树中的所有节点,使每个节点被且仅被访问一次。二叉树的遍历方式主要有:先序遍历、中序遍历、后序遍历、层次遍历。
- 先序遍历:根节点 -> 左子树 -> 右子树
- 中序遍历:左子树 -> 根节点 -> 右子树
- 后序遍历:左子树 -> 右子树 -> 根节点
- 层次遍历:按照从上到下顺序访问每个节点
3.2前序遍历
先序遍历:根节点 -> 左子树 -> 右子树,依次打印节点
遍历结果:1、2、 4 、 5、 3 、6
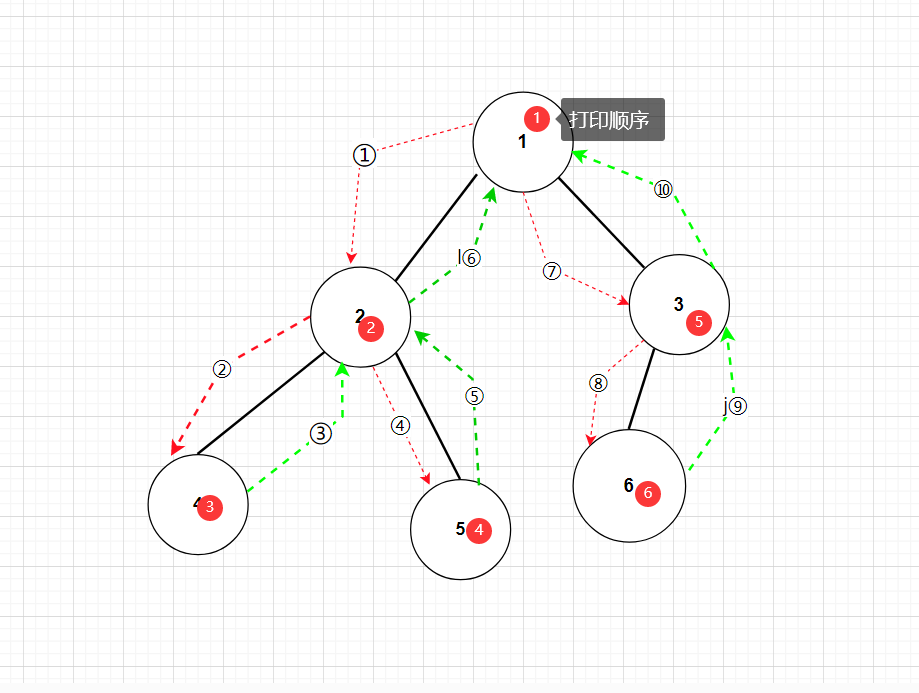
首先访问根节点1,打印1,然后递归地访问左子树和右子树。在左子树中,打印2,站在节点2的视角,也是一棵二叉树,节点2是这棵二叉树的根节点,于是又要先访问节点2的左子树,打印4,站在节点4的角度,节点4是根节点,节点4也有左子树和右子树,于是又要再去访问节点4的左子树,4的左子树为空,递归回来,访问节点4的右子树,右子树为空,递归回来。然后访问节点2的右子树;
递归回来,此时站在根节点1的视角,它的左子树遍历完了,于是访问右子树,站在右子树的视角,它此时也是一个独立 的二叉树,打印3后,于是要访问节点3的左子树和右子树。
以此类推,如下图,因此每个节点可以当做是一个二叉树,由多个小的二叉树结合成一个大的二叉树。

3.2 中序遍历
中序遍历:左子树 -> 根节点 -> 右子树依次打印节点
遍历结果:4、 2 、5、 1、6、3
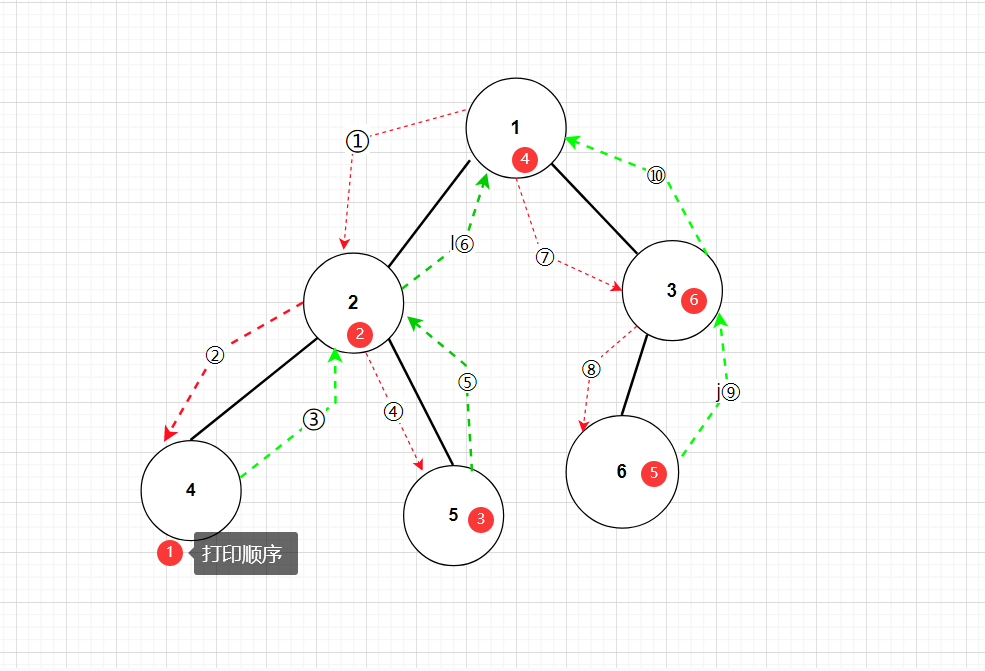
**还是一样的图,只是访问的根节点的时机不一样!前序遍历,先打印根节点,中序遍历先打印最左的一个节点,后续遍历,最后打印根节点!**进来先访问到了根节点1,不打印,直到把左子树走完,此时遍历到了节点4,4没有左子树,于是递归回来打印4,4没有右子树,递归回来打印2,只有把节点2的左子树遍历完后,才会打印2;依次类推。所以只有把每个节点的左子树遍历完,才会打印当前节点,然后再去遍历右子树,右子树也有它的左子树,同理。
3.3 后序遍历
后序遍历:左子树 -> 右子树 -> 根节点
遍历结果:4、 5、 2、 6、 3、 1
根据前中后序遍历,得出,后序遍历,只有当左子树和右子树遍历完,才会回来打印根节点。

遍历开始,遇到1,不能打印,只有把1的左子树和右子树遍历完才能打印1,
走到节点2,不能打印,要先把节点2的左子树和右子树遍历完才能打印2,
走到4,由于4的左子树和右子树为空,递归回来打印4,
走到5,由于5的左子树和右子树为空,递归回来打印5,
此时再递归回来就可以打印节点2了,因为2的左子树和右子树都遍历完了。
依次类推,最后才能打印根节点1。
- 得出一个规律:前序遍历的第一个打印的节点肯定是根节点,后序遍历最后打印的节点肯定是根节点。【重点】
根据上述规律,做出这道题:
1.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为()
A: adbce B: decab C: debac D: abcde
根据规律可以画出如下图:
根据后序遍历,最后一个打印的节点是a,那么a肯定就是这颗二叉树的根节点,再根据中序遍历,按照a的位置,划分左右子树,a的左边是a的左子树,a的右边是a的右子树,由于a的右边有多个节点,不确定哪个节点是a的孩子节点,所以要继续化简,于是得出:

再根据后序遍历的倒数第二个节点,因为后序遍历中的a已经被刨除出去了,所以当前后序遍历的最后一个节点是c,再根据规律后序遍历的最后一个节点肯定是根节点,按照c的位置,划分出中序遍历的左右子树,在中序遍历中,c的左边是c的左子树,c的右边是c的右子树,由于c的左右皆剩下1个节点,那么这两个节点就是c的孩子节点,于是得出:
,因为后序遍历中的a已经被刨除出去了,所以当前后序遍历的最后一个节点是c,再根据规律后序遍历的最后一个节点肯定是根节点,按照c的位置,划分出中序遍历的左右子树,在中序遍历中,c的左边是c的左子树,c的右边是c的右子树,由于c的左右皆剩下1个节点,那么这两个节点就是c的孩子节点,于是得出:
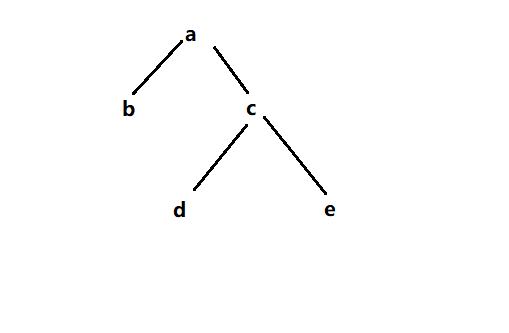
答案是:D
相关文章:

二叉树的性质、前中后序遍历【详细】
1. 树概念2.二叉树的概念1.2二叉树的性质 3.二叉树遍历3.2前序遍历3.2 中序遍历3.3 后序遍历 1. 树概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合,有二叉树,N叉树等等。 子树…...

涨姿势了,有意思的气泡 Loading 效果
今日,群友提问,如何实现这么一个 Loading 效果: 这个确实有点意思,但是这是 CSS 能够完成的? 没错,这个效果中的核心气泡效果,其实借助 CSS 中的滤镜,能够比较轻松的实现࿰…...
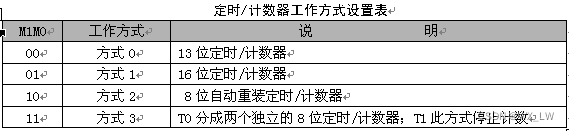
单片机中断系统
单片机中断系统 中断的概念: CPU在处理某一事件A时,发生了另一事件B请求CPU迅速去处理(中断发生);CPU暂时中断当前的工作,转去处理事件B(中断响应和中断服务);待CPU将事…...
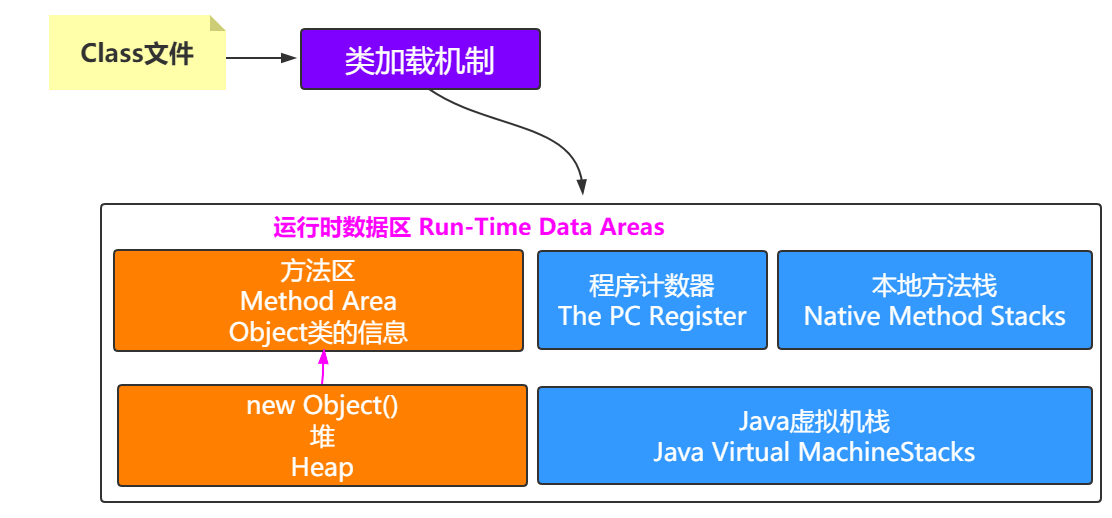
二、JVM-深入运行时数据区
深入运行时数据区 计算机体系结构 JVM的设计实际上遵循了遵循冯诺依曼计算机结构 CPU与内存交互图: 硬件一致性协议: MSI、MESI、MOSI、Synapse、Firely、DragonProtocol 摩尔定律 摩尔定律是由英特尔(Intel)创始人之一戈登摩尔(Gordon Moore)提出来…...

随机验证码vue实现,登录验证码随机验证码数字和字母类型的
1、组件 <!--loginCode登录验证码组件--> <template> <canvas id"canvasCode" :width"contentWidth" :height"contentHeight" /> </template> <script> export default { name: LoginCode, props: { identif…...
xlrd与xlwt操作Excel文件详解
Python操作Excel的模块有很多,并且各有优劣,不同模块支持的操作和文件类型也有不同。下面是各个模块的支持情况: .xls.xlsx获取文件内容写入数据修改文件内容保存样式调整插入图片xlrd√√√xlwt√√√√√xlutils√√√√xlwings√√√√√…...
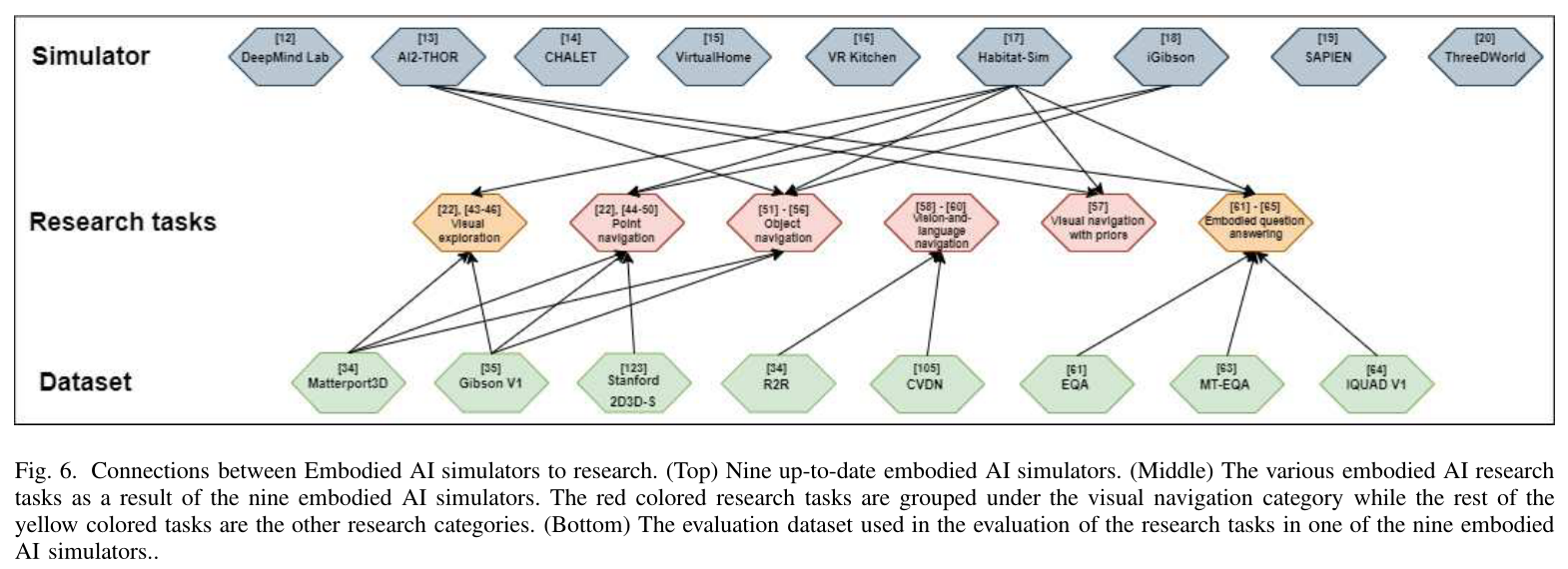
A Survey of Embodied AI: From Simulators to Research Tasks 论文阅读
论文信息: 题目:A Survey of Embodied AI: From Simulators to Research Tasks 作者:Jiafei Duan, Samson Yu 来源:arXiv 时间:2022 Abstract 通过评估当前的九个具体人工智能模拟器与我们提出的七个功能࿰…...

spark-sql数据重复之File Output Committer问题
前言 我们先来回顾下之前介绍过的三种Committer:FileOutputCommitter V1、FileOutputCommitter V2、S3A Committer,其基本代表了整体的演进趋势。 核心代码讲解详细参照:Spark CommitCoordinator 保证数据一致性 OutputCommitter commitTask…...
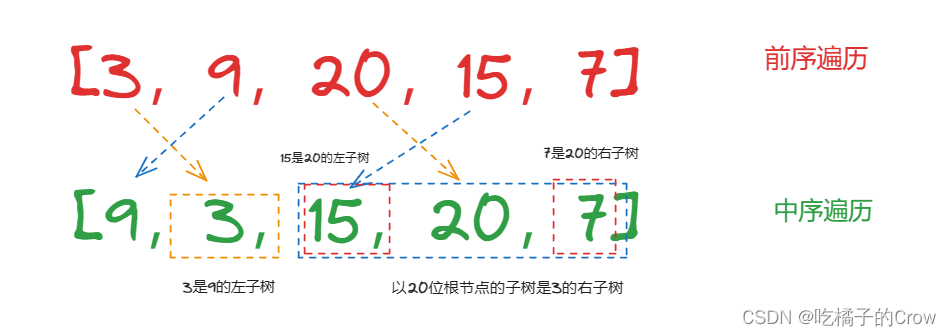
面试热题(前中序遍历构建树)
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。 题目中是给定两个数组,一个是存放这颗树的前序遍历的数组,一个是存放这棵树的…...

美术:贴图
游戏模型制作流程,SP和BP根据情况来选择软件对UV进行处理 3Dmax 制作模型和动画(橘肉)RizomUV 对模型进行展UV(橘皮)Substance Painter 纹理手绘(给橘皮制定想要的皮肤)BodyPaint 3D 纹理手绘&a…...

[MAUI]模仿微信“按住-说话”的交互实现
今天使用这个控件,做一个模仿微信“按住-说话”的小功能,最终效果如下: 使用.NET MAUI实现跨平台支持,本项目可运行于Android、iOS平台。 创建页面布局 新建.NET MAUI项目,命名HoldAndSpeak MainPage.xaml中创建一个…...
windows开机运行jar
windows开机自启动jar包: 一、保存bat批处理文件 echo off %1 mshta vbscript:CreateObject("WScript.Shell").Run("%~s0 ::",0,FALSE)(window.close)&&exit java -jar E:\projects\ruoyi-admin.jar > E:\server.log 2>&1 &…...

使用DockerFile一键创建自定义linux开发环境
1,使用dcokerfile文件构建镜像,参考如下文件 # 使用ubuntu:20.04镜像作为基础 FROM ubuntu:20.04# 调整时区 ENV DEBIAN_FRONTENDnoninteractive TZAsia/Shanghai# build参数 ARG userxiang usergroupduo# 设置默认工作路径 WORKDIR /home/${user}# 拷贝…...

“深入探索JVM:解密Java虚拟机的工作原理“
标题:深入探索JVM:解密Java虚拟机的工作原理 摘要:本文将深入探索Java虚拟机(JVM)的工作原理,从字节码到实际执行过程,从内存管理到垃圾回收等方面进行解析,帮助读者更好地理解和优…...

【华为OD机试】数字最低位排序【2023 B卷|100分】
【华为OD机试】-真题 !!点这里!! 【华为OD机试】真题考点分类 !!点这里 !! 题目描述 给定一个非空数组(列表) 起元素数据类型为整型 请按照数组元素十进制最低位从小到大进行排序 十进制最低位相同的元素,相对位置保持不变 当数组元素为负值时,十进制最低为等同于去除符号…...

【Odoo16前端源码分析】xml模板的加载
一、模板内容的来源 情况A,组件类的template属性,比如ActionContainer.template /* odoo/addons/web/static/src/webclient/actions/action_container.js */export class ActionContainer extends Component {setup() {..} } .. ActionContainer.templ…...

Open3D (C++) 计算矩阵的广义逆
目录 一、算法原理1、广义逆2、计算过程二、代码实现三、结果展示四、参考链接本文由CSDN点云侠原创,原文链接。爬虫网站自重,把自己当个人,爬些不完整的误导别人有意思吗???? 一、算法原理 1、广义逆 非方阵不存在逆,但是存在广义逆(伪逆)。对于一个矩阵...
11.物联网操作系统内存管理
一。STM32编译过程及程序组成 STM32编译过程 程序的组成、存储与运行 MDK生成的主要文件分析 1.STM32编译过程 1.源文件(Source code)--》目标文件(Object code) .c(C语言)通过armcc生成.o,.s(汇编&…...
举办活动发布会,如何得到媒体支持?
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 举办活动发布会并得到媒体报道的支持是一个关键的宣传和推广手段。以下是一些建议,帮助你增加吸引媒体关注和报道的机会: 1. 策划新闻价值:确保你的发…...
函数))
1139 First Contact(unique函数,string.substr()函数)
PTA | 程序设计类实验辅助教学平台 用map套个set来实现邻接表(排序都免了) #include<bits/stdc.h> using namespace std; int n,m,k; string a,b; map<string,set<string>>mp; int main() {cin.tie(0);cin >> n >> m;fo…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
