机器学习笔记之优化算法(七)线搜索方法(步长角度;非精确搜索;Wolfe Condition)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索,Wolfe Condition]
引言
上一节介绍了 Glodstein \text{Glodstein} Glodstein准则 ( Glodstein Condition ) (\text{Glodstein Condition}) (Glodstein Condition)及其弊端。本节将针对该弊端,介绍 Wolfe \text{Wolfe} Wolfe准则 ( Wolfe Condition ) (\text{Wolfe Condition}) (Wolfe Condition)。
回顾:
Armijo \text{Armijo} Armijo准则及其弊端
在当前迭代步骤中,为了能够得到更精炼的 ϕ ( α ) \phi(\alpha) ϕ(α)选择范围, Armijo \text{Armijo} Armijo准则 ( Armijo Condition ) (\text{Armijo Condition}) (Armijo Condition)提出一种关于 ϕ ( α ) \phi(\alpha) ϕ(α)的筛选方式,使其比 ϕ ( α ) < f ( x k ) \phi(\alpha) < f(x_k) ϕ(α)<f(xk)更加严格:
Armijo Condition : { ϕ ( α ) < L ( α ) = f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α C 1 ∈ ( 0 , 1 ) \text{Armijo Condition : } \begin{cases} \phi(\alpha) < \mathcal L(\alpha) = f(x_k) + \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \\ \quad \\ \mathcal C_1 \in (0,1) \end{cases} Armijo Condition : ⎩ ⎨ ⎧ϕ(α)<L(α)=f(xk)+C1⋅[∇f(xk)]TPk⋅αC1∈(0,1)
这种操作产生的弊端是: C 1 \mathcal C_1 C1在取值过程中,可能出现数量较少的、并且并非 ϕ ( α ) \phi(\alpha) ϕ(α)主要部分的选择空间。见下图:

这种情况可能导致:
下面的两种情况都指向同一个问题: L ( α ) \mathcal L(\alpha) L(α)所划分的 α \alpha α范围从整个 ϕ ( α ) \phi(\alpha) ϕ(α)角度观察,是片面的、局部的。
- 可选择的 α \alpha α范围较小;
- 该小范围内的 α \alpha α结果,其对应的 ϕ ( α ) \phi(\alpha) ϕ(α)并不优质。
这里的‘优质’是指与整个ϕ ( α ) \phi(\alpha) ϕ(α)函数结果相比都属于一个较小的结果。最优质的自然是α ∗ = arg min α > 0 ϕ ( α ) \alpha^* = \mathop{\arg\min}\limits_{\alpha > 0} \phi(\alpha) α∗=α>0argminϕ(α),但我们在每次迭代过程中并不执著于α ∗ \alpha^* α∗,仅希望选择出的α \alpha α结果能够有效地使{ f ( x k ) } k = 0 ∞ \{f(x_{k})\}_{k=0}^{\infty} {f(xk)}k=0∞收敛到最优值f ∗ f^* f∗。
Glodstein \text{Glodstein} Glodstein准则及其弊端
针对 Armijo \text{Armijo} Armijo准则的问题, Glodstein \text{Glodstein} Glodstein准则在其基础上添加一个下界:
Glodstein Condition : { f ( x k ) + ( 1 − C ) ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ⏟ Lower Bound ≤ ϕ ( α ) ≤ f ( x k ) + C ⋅ [ ∇ f ( x k ) ] T P k ⋅ α C ∈ ( 0 , 1 2 ) \text{Glodstein Condition : } \begin{cases} \begin{aligned} & \underbrace{f(x_k) + (1 - \mathcal C) \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha}_{\text{Lower Bound}} \leq \phi(\alpha) \leq f(x_k) + \mathcal C \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \\ & \mathcal C \in \left(0,\frac{1}{2}\right) \end{aligned} \end{cases} Glodstein Condition : ⎩ ⎨ ⎧Lower Bound f(xk)+(1−C)⋅[∇f(xk)]TPk⋅α≤ϕ(α)≤f(xk)+C⋅[∇f(xk)]TPk⋅αC∈(0,21)
其中分别描述上界、下界的划分函数:
- Upper Bound : L U ( α ) = f ( x k ) + C ⋅ [ ∇ f ( x k ) ] T P k ⋅ α \text{Upper Bound : } \begin{aligned}\mathcal L_{\mathcal U}(\alpha) = f(x_k) + \mathcal C \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha\end{aligned} Upper Bound : LU(α)=f(xk)+C⋅[∇f(xk)]TPk⋅α
- Lower Bound : L L ( α ) = f ( x k ) + ( 1 − C ) ⋅ [ ∇ f ( x k ) ] T P k ⋅ α \text{Lower Bound : } \mathcal L_{\mathcal L}(\alpha) = f(x_k) + (1 - \mathcal C) \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha Lower Bound : LL(α)=f(xk)+(1−C)⋅[∇f(xk)]TPk⋅α
关于 f ( x k ) + 1 2 [ ∇ f ( x k ) ] T P k ⋅ α \begin{aligned}f(x_k) + \frac{1}{2} [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha\end{aligned} f(xk)+21[∇f(xk)]TPk⋅α对称。这能保证满足该范围的 α \alpha α结果,其对应的 ϕ ( α ) \phi(\alpha) ϕ(α)总是位于 ϕ ( α ) \phi(\alpha) ϕ(α)的核心部分,而不是片面的、局部的部分。见下图:
其中两条绿色实线之间区域内的 ϕ ( α ) \phi(\alpha) ϕ(α)结果相比 Armijo \text{Armijo} Armijo准则,其描述的范围更加核心。

但 Goldstein \text{Goldstein} Goldstein准则自身同样存在弊端:当参数 C \mathcal C C靠近 1 2 \begin{aligned}\frac{1}{2}\end{aligned} 21时,对应上下界包含的 ϕ ( α ) \phi(\alpha) ϕ(α)结果极少。从而可能使一些优质 α \alpha α结果丢失。见下图:

Wolfe Condition \text{Wolfe Condition} Wolfe Condition
首先,我们可以发现一个关于 Armijo \text{Armijo} Armijo准则与 Goldstein \text{Goldstein} Goldstein准则的共同问题:被选择的仅仅是满足划分边界条件的 α \alpha α结果,而被选择的 α \alpha α结果是否存在被选择的意义是未知的。
换句话说,基于这两种准则选择出的 α \alpha α结果仅仅是因为:
该α \alpha α对应的ϕ ( α ) \phi(\alpha) ϕ(α)位于决策边界L ( α ) = f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α \mathcal L(\alpha) = f(x_k) + \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha L(α)=f(xk)+C1⋅[∇f(xk)]TPk⋅α的下方( Armijo Condition ) (\text{Armijo Condition}) (Armijo Condition);该α \alpha α对应的ϕ ( α ) \phi(\alpha) ϕ(α)位于上决策边界L U ( α ) \mathcal L_{\mathcal U}(\alpha) LU(α)与下决策边界L L ( α ) \mathcal L_{\mathcal L}(\alpha) LL(α)所围成的范围之间( Glodstein Condition ) (\text{Glodstein Condition}) (Glodstein Condition)。
这意味着:我们确实得到了若干 α \alpha α结果,但是这些结果是否优质属于未知状态。
我们尝试从满足 Armijo \text{Armijo} Armijo准则的基础上,通过某种规则剔除掉部分没有竞争力的 α \alpha α结果,从而在剩余结果中找到优质的 α \alpha α结果。见下图:

初始状态下,我们找到了一个 C 1 ∈ ( 0 , 1 ) \mathcal C_1 \in (0,1) C1∈(0,1),并描述出了它的划分边界 L ( α ) \mathcal L(\alpha) L(α);由于 L ( α ) \mathcal L(\alpha) L(α)的斜率 C 1 ⋅ [ ∇ f ( x k ) ] T P k \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k C1⋅[∇f(xk)]TPk必然大于 l ( α ) l(\alpha) l(α)的斜率 [ ∇ f ( x k ) ] T P k [\nabla f(x_k)]^T \mathcal P_k [∇f(xk)]TPk,因此从 α = 0 \alpha = 0 α=0出发,找到切线斜率与 L ( α ) \mathcal L(\alpha) L(α)斜率相同的点:
下图中的绿色虚线表示切线斜率与 L ( α ) \mathcal L(\alpha) L(α)斜率相同的 α \alpha α点,短绿线表示寻找过程,点 A \mathcal A A表示满足条件的切点。

通过观察可以发现:点 A \mathcal A A必然不是极值点(虽然看起来有点像~),因为该点处的斜率 ≠ 0 \neq 0 =0。这里能够确定:从 [ 0 , f ( x k ) ] [0,f(x_k)] [0,f(xk)]到 A \mathcal A A点这一段函数内的所有点相比于 A \mathcal A A都没有竞争力。而这些点的切线斜率 ϕ ′ ( α ) \phi'(\alpha) ϕ′(α)满足:
[ ∇ f ( x k ) ] T P k ≤ ϕ ′ ( α ) ≤ C 1 ⋅ [ ∇ f ( x k ) ] T P k [\nabla f(x_k)]^T \mathcal P_k \leq \phi'(\alpha) \leq \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k [∇f(xk)]TPk≤ϕ′(α)≤C1⋅[∇f(xk)]TPk
关于仅与参数 C 1 \mathcal C_1 C1相关的武断做法
如果将这些没有竞争力的点去除掉,保留剩余的点,结合 Armijo \text{Armijo} Armijo准则,会有如下的步长 α \alpha α选择方式:
其中ϕ ′ ( α ) = ∂ f ( x k + α ⋅ P k ) ∂ α = [ ∇ f ( x k + α ⋅ P k ) ] T P k \begin{aligned}\phi'(\alpha) = \frac{\partial f(x_k + \alpha \cdot \mathcal P_k)}{\partial \alpha} = [\nabla f(x_k + \alpha \cdot \mathcal P_k)]^T \mathcal P_k\end{aligned} ϕ′(α)=∂α∂f(xk+α⋅Pk)=[∇f(xk+α⋅Pk)]TPk,在后续的计算中均简化写作ϕ ′ ( α ) \phi'(\alpha) ϕ′(α)。关于斜率ϕ ′ ( α ) ≤ C 1 ⋅ [ ∇ f ( x k ) ] T P k \phi'(\alpha)\leq \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k ϕ′(α)≤C1⋅[∇f(xk)]TPk点不再理会,而[ ∇ f ( x k ) ] T P k [\nabla f(x_k)]^T \mathcal P_k [∇f(xk)]TPk是ϕ ( 0 ) \phi(0) ϕ(0)的斜率,作为下界。
{ ϕ ( α ) ≤ f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ϕ ′ ( α ) ≥ C 1 ⋅ [ ∇ f ( x k ) ] T P k C 1 ∈ ( 0 , 1 ) \begin{cases} \phi(\alpha) \leq f(x_k) + \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \\ \phi'(\alpha) \geq \mathcal C_1 \cdot [\nabla f(x_{k})]^T \mathcal P_k \\ \mathcal C_1 \in (0,1) \end{cases} ⎩ ⎨ ⎧ϕ(α)≤f(xk)+C1⋅[∇f(xk)]TPk⋅αϕ′(α)≥C1⋅[∇f(xk)]TPkC1∈(0,1)
基于上述逻辑,被选择的 ϕ ( α ) \phi(\alpha) ϕ(α)见下图:
其中 A ′ \mathcal A' A′点表示该图像中斜率与 L ( α ) \mathcal L(\alpha) L(α)相同的其他位置的点。

上述这种方式可取吗 ? ? ?从逻辑角度上是可行的,但不可取。
关于 C 1 \mathcal C_1 C1武断做法不可取的逻辑解释
-
由于 C 1 ∈ ( 0 , 1 ) \mathcal C_1 \in (0,1) C1∈(0,1),因而 C 1 ⋅ [ ∇ f ( x k ) ] T P k < 0 \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k < 0 C1⋅[∇f(xk)]TPk<0恒成立。也就是说:无论 C 1 \mathcal C_1 C1如何趋近于 0 0 0, Armijo \text{Armijo} Armijo准则划分边界 L ( α ) \mathcal L(\alpha) L(α)如何趋近于 ϕ ( α ) = f ( x k ) \phi(\alpha) = f(x_k) ϕ(α)=f(xk),都无法获取使 ϕ ′ ( α ) = 0 \phi'(\alpha) = 0 ϕ′(α)=0的极值解。
很简单,就是因为取不到~而与此同时,我们为了追求这个极值解,可能反而会损失一系列 ϕ ( α ) \phi(\alpha) ϕ(α)优质的 α \alpha α点。
如果仅使用C 1 \mathcal C_1 C1一个参数,那么要去除的点在Armijo \text{Armijo} Armijo准则划分边界L ( α ) \mathcal L(\alpha) L(α)确定的那一刻就已经被确定了,这势必会误伤一些ϕ ( α ) \phi(\alpha) ϕ(α)优质的α \alpha α结果。 -
其次,这里的操作是非精确搜索,因而不执著去追求极值解(那不就变成精确搜索了吗~),并且这仅仅是一次迭代的计算过程,没有必要消耗计算代价去追求更优质的 ϕ ( α ) \phi(\alpha) ϕ(α),这也是我们希望尽量保留 ϕ ( α ) \phi(\alpha) ϕ(α)优质解的核心原因:
与上一张图被选择的ϕ ( α ) \phi(\alpha) ϕ(α)值对比观察,红色椭圆形虚线区域中描述的ϕ ( α ) \phi(\alpha) ϕ(α)值是比较优质的,但因为C 1 \mathcal C_1 C1的原因导致该部分结果被‘一刀切’了。这并不是我们希望看到的结果。

关于 C 1 \mathcal C_1 C1武断做法的改进: Wolfe Condition \text{Wolfe Condition} Wolfe Condition
如何避免上述一刀切的情况出现 ? ? ? Wolfe \text{Wolfe} Wolfe准则提供了而一种更软性的操作。
设置一个参数 C 2 ∈ ( C 1 , 1 ) \mathcal C_2 \in (\mathcal C_1,1) C2∈(C1,1),该参数对应的斜率表示为 C 2 ⋅ [ ∇ f ( x k ) ] T P k \mathcal C_2 \cdot [\nabla f(x_k)]^T \mathcal P_k C2⋅[∇f(xk)]TPk,而该斜率在 ( [ ∇ f ( x k ) ] T P k , C 1 ⋅ [ ∇ f ( x k ) ] T P k ) ([\nabla f(x_k)]^T \mathcal P_k,\mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k ) ([∇f(xk)]TPk,C1⋅[∇f(xk)]TPk)之间滑动(变换)。此时会出现一种缓和的情况:即便假设 C 1 \mathcal C_1 C1无限接近于 0 0 0,但由于 C 2 \mathcal C_2 C2的作用,使 ϕ ( α ) \phi(\alpha) ϕ(α)点的选择与 C 1 \mathcal C_1 C1没有太大关联:
这里相当于将斜率C 1 ⋅ [ ∇ f ( x k ) ] T P k \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k C1⋅[∇f(xk)]TPk视作一个边界。上面的一刀切情况相当于C 1 ⇒ 0 \mathcal C_1 \Rightarrow 0 C1⇒0的同时,C 2 ⇒ C 1 \mathcal C_2 \Rightarrow\mathcal C_1 C2⇒C1的情况。由于C 2 ∈ ( C 1 , 1 ) \mathcal C_2 \in (\mathcal C_1,1) C2∈(C1,1)因而完全可以通过调整 C 2 \mathcal C_2 C2针对那些斜率小于 C 1 ⋅ [ ∇ f ( x k ) ] T P k \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k C1⋅[∇f(xk)]TPk,但 ϕ ( α ) \phi(\alpha) ϕ(α)优质的结果进行酌情选择。
最终根据 Armijo \text{Armijo} Armijo准则, Wolfe \text{Wolfe} Wolfe准则操作如下:
{ ϕ ( α ) ≤ f ( x k ) + C 1 [ ∇ f ( x k ) ] T P k ⋅ α ϕ ′ ( α ) ≥ C 2 ⋅ [ ∇ f ( x k ) ] T P k C 1 ∈ ( 0 , 1 ) C 2 ∈ ( C 1 , 1 ) \begin{cases} \phi(\alpha) \leq f(x_k) + \mathcal C_1 [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \\ \phi'(\alpha) \geq \mathcal C_2 \cdot [\nabla f(x_k)]^T \mathcal P_k \\ \mathcal C_1 \in (0,1) \\ \mathcal C_2 \in (\mathcal C_1,1) \end{cases} ⎩ ⎨ ⎧ϕ(α)≤f(xk)+C1[∇f(xk)]TPk⋅αϕ′(α)≥C2⋅[∇f(xk)]TPkC1∈(0,1)C2∈(C1,1)
个人理解: Wolfe \text{Wolfe} Wolfe准则与 Armijo \text{Armijo} Armijo准则
在开头部分提到关于 Armijio \text{Armijio} Armijio准则的弊端,在介绍完 Wolfe \text{Wolfe} Wolfe准则之后,有种 Armijo \text{Armijo} Armijo准则的弊端卷土重来的感觉。个人认为: Wolfe \text{Wolfe} Wolfe准则提出的这种基于 C 2 ∈ ( C 1 , 1 ) \mathcal C_2 \in (\mathcal C_1,1) C2∈(C1,1)的软性下界同样也在影响 C 1 \mathcal C_1 C1的选择:
- 如果是单纯的 Armijo \text{Armijo} Armijo准则,我们可能更偏好 C 1 \mathcal C_1 C1远离 0 0 0一些。因为 C 1 ⇒ 0 \mathcal C_1 \Rightarrow 0 C1⇒0意味着这种状态越趋近优化算法(四)中描述的必要不充分条件;这种 C 1 \mathcal C_1 C1的选择方式也势必会增加 Armijo \text{Armijo} Armijo准则弊端的风险;
- 而 Wolfe \text{Wolfe} Wolfe准则中,即便 C 1 \mathcal C_1 C1偏向 0 0 0方向,我们依然可以通过调整 C 2 \mathcal C_2 C2对相对不优质的 ϕ ( α ) \phi(\alpha) ϕ(α)点进行过滤。从剩余的优质点中选择并进行迭代。
相关参考:
【优化算法】线搜索方法-步长-Wolfe Condition
相关文章:

机器学习笔记之优化算法(七)线搜索方法(步长角度;非精确搜索;Wolfe Condition)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索,Wolfe Condition] 引言回顾: Armijo \text{Armijo} Armijo准则及其弊端 Glodstein \text{Glodstein} Glodstein准则及其弊端 Wolfe Condition \text{Wolfe Condition} Wolfe Condi…...
十四.redis哨兵模式
redis哨兵模式 1.概述2.测试3.哨兵模式优缺点 redis哨兵模式基础是主从复制 1.概述 主从切换的技术方法:当主节点服务器宕机后,需要手动把一台从服务器切换为主服务器,这就需要人工干预,费时费力,还会造成一段时间内服…...
采用UWB技术开发的智慧工厂人员定位系统源码【UWB定位基站、卡牌】
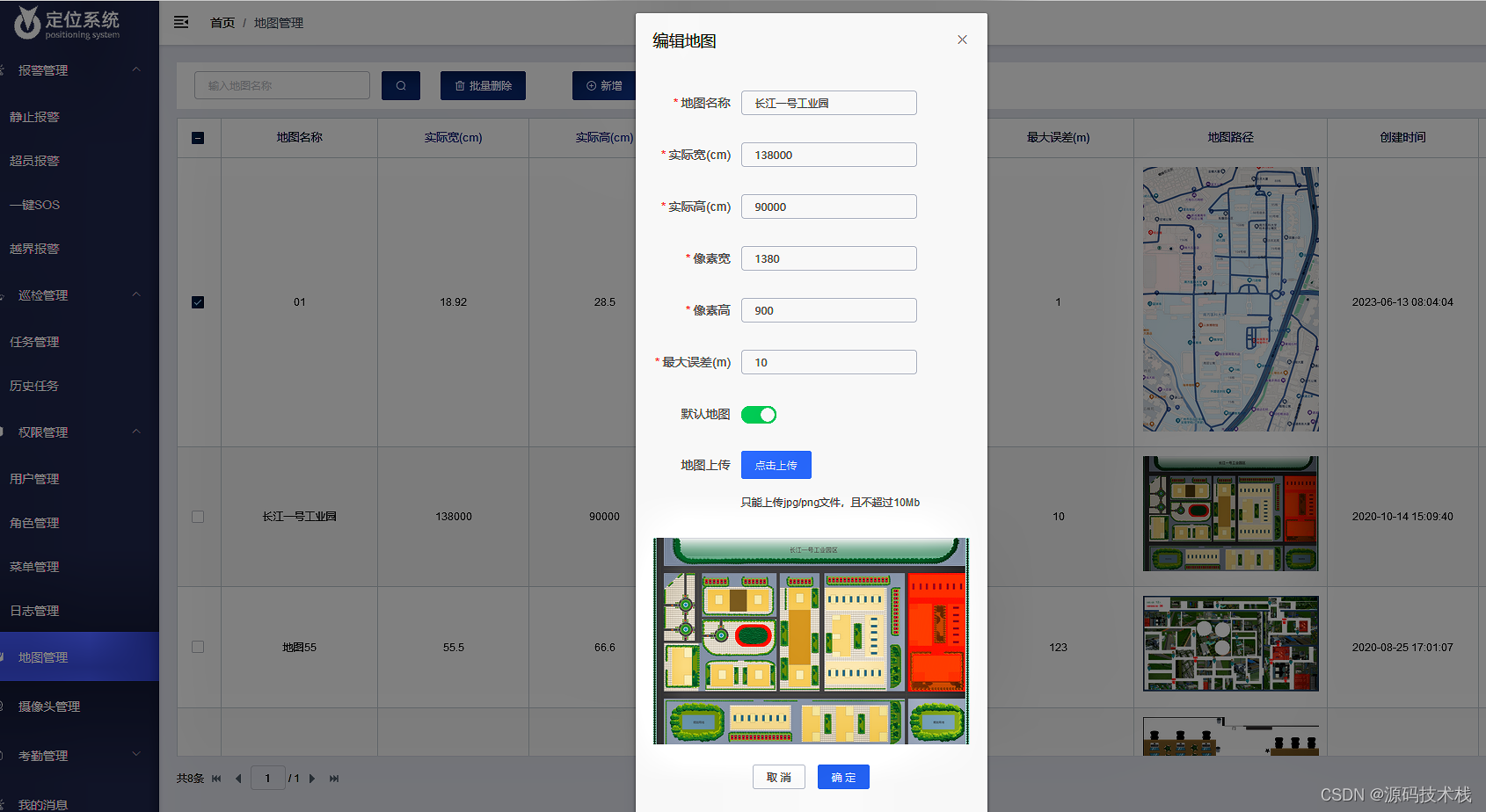
UWB (ULTRA WIDE BAND, UWB) 技术是一种无线载波通讯技术,它不采用正弦载波,而是利用纳秒级的非正弦波窄脉冲传输数据,因此其所占的频谱范围很宽。UWB定位系统依托在移动通信,雷达,微波电路,云计算与大数据…...
当你软件测试遇上加密接口,是不是就不能测了?
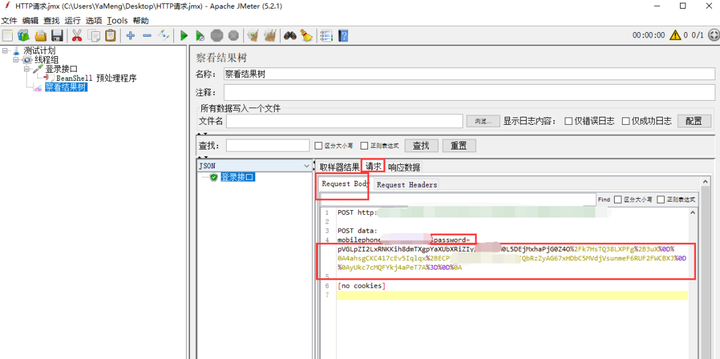
相信大家在工作中做接口测试的时候,肯定会遇到一个场景,那就是你们的软件,密码是加密存储的。 那么这样的话,我们在执行接口的时候,对于密码的处理就开始头疼了。 所以,本文将使用jmeter这款java开源的接…...

Flink
Flink(Apache Flink)是一个开源的分布式流处理引擎和批处理框架。它是由 Apache 软件基金会维护的项目,旨在处理大规模数据的实时流式处理和批处理任务。Flink 提供了强大的流处理和批处理功能,具有低延迟、高吞吐量和高容错性&am…...

python入门常用操作
python常用操作 1、ndarry数组的切片2、print用法2.1格式化输出format2.2字符串格式化输出 3、均值滤波函数 1、ndarry数组的切片 例如一个5列的ndarry数组,想要获取第2列和第3列数据,可以用 #(1)用法1 data[:,1:3],…...
自定义ImportBeanDefinitionRegistrar)
SpringBoot复习:(21)自定义ImportBeanDefinitionRegistrar
要达到的目的:将某个包下使用了某个自定义注解(比如MyClassMapper)的类注册到Spring 容器。 一、自定义注解: package com.example.demo.service;import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy;Rete…...

小黑子—JavaWeb:第五章 - JSP与会话跟踪技术
JavaWeb入门5.0 1. JSP1.1 JSP快速入门1.2 JSP原理1.3 JSP脚本1.3.1 JSP缺点 1.4 EL 表达式1.5 JSTL 标签1.5.1 JSTL 快速入门1.5.1 - I JSTL标签if1.5.1 - II JSTL标签forEach 1.6 MVC模式1.7 三层架构1.8 实现案例1.8.1 环境准备1.8.2 查询所有1.8.3 添加数据1.8.4 修改1.8.4…...

Python - 【socket】 客户端client重连处理简单示例Demo(一)
一. 前言 在Python中,使用socket进行网络通信时,如果连接断开,可以通过以下步骤实现重连处理 二. 示例代码 1. 定义一个函数,用于建立socket连接 import socketdef connect_socket(host, port):while True:try:# 建立socket连…...
Redis 基础
1.定义 Redis 是一个高性能的key-value数据库,key是字符串类型。 2.核心特点: 单进程: Redis的服务器程序采用的是单进程模型来处理客户端的请求。对读写时间的响 应是通过对epoll函数的包装来做到的。 3.数据类型: 键的类型…...

【0805作业】Linux中 AB终端通过两根有名管道进行通信聊天(半双工)
作业一:打开两个终端,要求实现AB进程对话【两根管道】 打开两个终端,要求实现AB进程对话 A进程先发送一句话给B进程,B进程接收后打印B进程再回复一句话给A进程,A进程接收后打印重复1.2步骤,当收到quit后&am…...

ruby - ckeditor 设置编辑器高度
参考:Blogs <% f.cktext_area :zh_content, ckeditor: { height: 1000} %>...
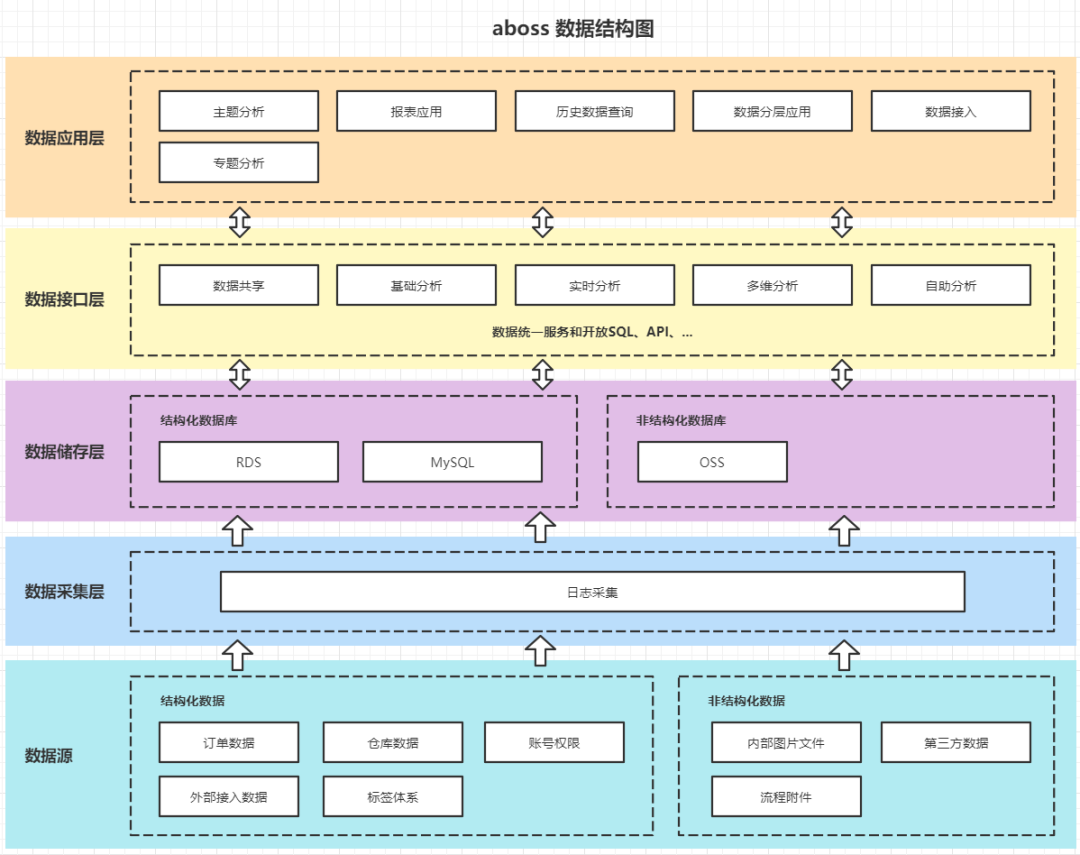
WMS仓库管理系统研发规划说明
01 产品背景 1.1 背景概述 aboss WMS东南亚仓库管理系统是一个基于BigSeller系统的使用基础上,加上多仓库的解决思路,解决入库业务、出库业务、仓库调拨、库存调拨和虚仓管理等功能,对批次管理、物料对应、库存盘点、质检管理、虚仓管理和即…...

JavaScript |(六)DOM事件 | 尚硅谷JavaScript基础实战
学习来源:尚硅谷JavaScript基础&实战丨JS入门到精通全套完整版 文章目录 📚事件对象📚事件的冒泡📚事件的委派📚事件的绑定🐇赋值绑定🐇addEventListener()🐇attachEvent()&…...
实验心得,包括代码复现工作的体会
实践是检验真理的唯一标准 resnet20,cifar100. Direct training: 和原论文一样的参数 64.45 time step 1, Accuracy 0.5918 time step 2, Accuracy 0.6320 time step 4, Accuracy 0.6446 time step 8, Accuracy 0.6531 time step 16, Accuracy 0.6608 time ste…...

RabbitMQ(二)
二、高级特性、应用问题以及集群搭建 高级特性 1.消息的可靠性投递 在使用RabbitMQ的时候,作为消息发送方希望杜绝任何消息丢失或者投递失败场景。RabbitMQ 为我们提供了两种方式用来控制消息的投递可靠性模式。 rabbitMQ整个消息投递的路径为: produ…...

Linux软件实操
systemctl命令 Linux系统的很多内置或第三方的软件均支持使用systemctl命令控制软件(服务)的启动、停止、开机自启 systemctl start(启动) 或 stop(关闭) 或 status(查看状态) 或 enable(开启开机自启) disable(关闭开机自启) 服务名: 控制服务的状态 系统内置的服务: Netwo…...
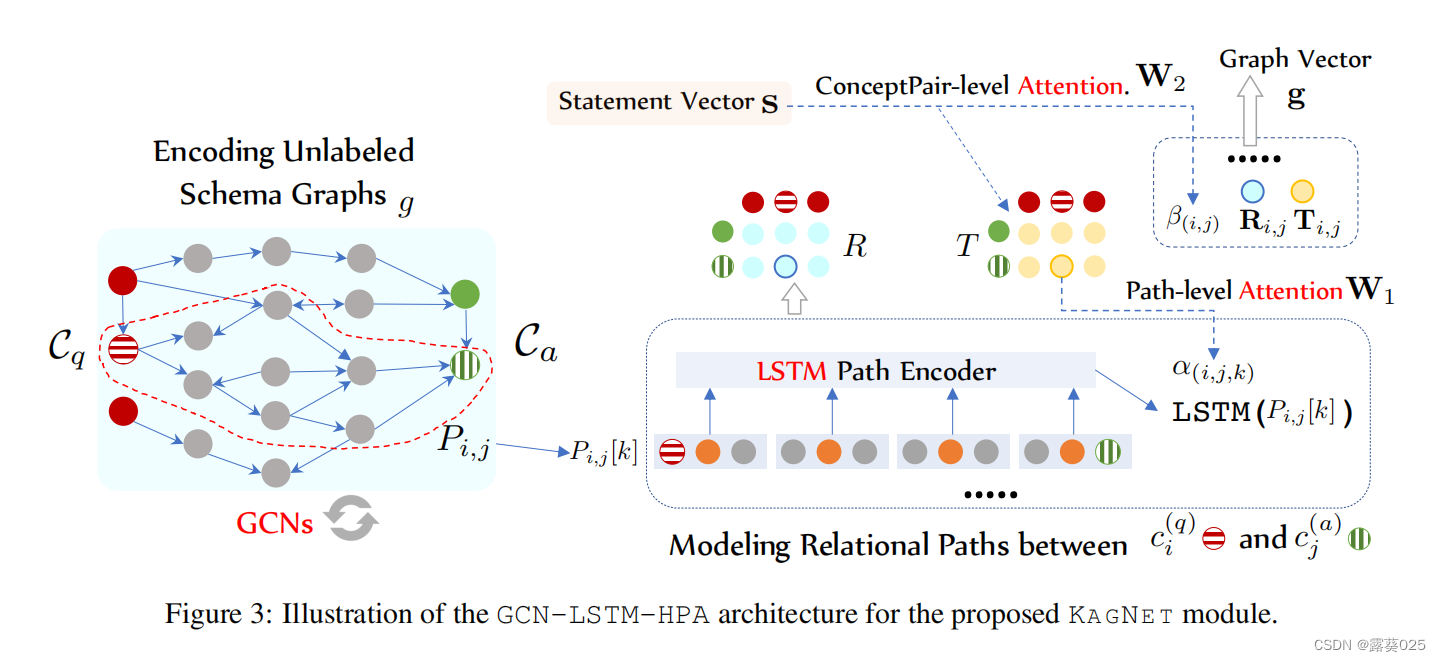
kagNet:对常识推理的知识感知图网络 8.4+8.5
这里写目录标题 摘要介绍概述问题陈述推理流程 模式图基础概念识别模式图构造概念网通过寻找路径来匹配子图基于KG嵌入的路径修剪 知识感知图网络图卷积网络(GCN)关系路径编码分层注意机制 实验数据集和使用步骤比较方法KAGNET是实施细节性能比较和分析I…...
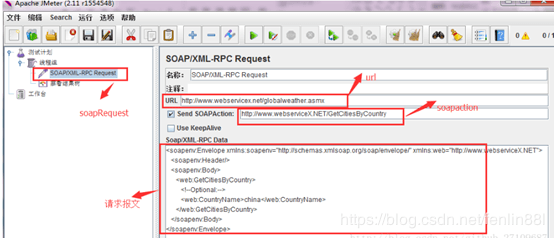
Jmeter 压测工具使用手册[详细]
1. jemter 简介 jmeter 是 apache 公司基于 java 开发的一款开源压力测试工具,体积小,功能全,使用方便,是一个比较轻量级的测试工具,使用起来非常简 单。因为 jmeter 是 java 开发的,所以运行的时候必须先…...
matlab智能算法程序包89套最新高清录制!matlab专题系列!
关于我为什么要做代码分享这件事? 助力科研旅程! 面对茫茫多的文献,想复现却不知从何做起,我们通过打包成品代码,将过程完善,让您可以拿到一手的复现过程以及资料,从而在此基础上,照…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
