第三章 图论 No.4最小生成树的简单应用
文章目录
- 裸题:1140. 最短网络
- 裸题:1141. 局域网
- 裸题:1142. 繁忙的都市
- 裸题:1143. 联络员
- 有些麻烦的裸题:1144. 连接格点
存在边权为负的情况下,无法求最小生成树

裸题:1140. 最短网络
1140. 最短网络 - AcWing题库
套个prim的板子即可
#include <iostream>
#include <cstring>
using namespace std;const int N = 110, INF = 0x3f3f3f3f;
int g[N][N];
int dis[N]; bool st[N];
int n;int prim()
{memset(dis, 0x3f, sizeof(dis));int res = 0;for (int i = 0; i < n; ++ i ){int x = -1;for (int j = 1; j <= n; ++ j ) if (!st[j] && (x == -1 || dis[x] > dis[j])) x = j;st[x] = true;if (i && dis[x] == INF) return INF;if (i) res += dis[x];for (int y = 1; y <= n; ++ y )dis[y] = min(dis[y], g[x][y]);}return res;
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; ++ i )for (int j = 1; j <= n; ++ j )scanf("%d", &g[i][j]);printf("%d\n", prim());return 0;
}
裸题:1141. 局域网
1141. 局域网 - AcWing题库
裸题,稀疏图,套个kruskal的板子就行
需要注意的是:题目给定的图可能存在多个连通块,若使用prim算法,需要对每个连通块求最小生成树,但是使用kruskal能直接求出所有连通块的最小生成树
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;const int N = 110, M = 210;
struct Edge
{int x, y, w;bool operator<(const Edge& e) const {return w < e.w;}
}edges[M];int p[N];
int n, m;int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int kruskal()
{sort(edges, edges + m);for (int i = 1; i <= n; ++ i ) p[i] = i;int cnt = 0, res = 0;for (int i = 0; i < m; ++ i ){auto t = edges[i];int x = edges[i].x, y = edges[i].y, w = edges[i].w;x = find(x), y = find(y);if (x != y){cnt ++ ;res += w;p[x] = y;}}return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i )scanf("%d%d%d", &edges[i].x, &edges[i].y, &edges[i].w);int sum = 0;for (int i = 0; i < m; ++ i ) sum += edges[i].w;printf("%d\n", sum - kruskal());return 0;
}
裸题:1142. 繁忙的都市
1142. 繁忙的都市 - AcWing题库
依然是套kruskal的板子
#include <iostream>
#include <algorithm>
using namespace std;const int N = 310 ,M = 8010;
struct Edge
{int x, y, w;bool operator<(const Edge& e) const{return w < e.w;}
}edges[M];int n, m;
int p[N];int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int kruskal()
{sort(edges, edges + m);int res = 0;for (int i = 1; i <= n; ++ i ) p[i] = i;for (int i = 0; i < m; ++ i ){auto t = edges[i];int x = t.x, y = t.y, w = t.w;x = find(x), y = find(y);if (x != y){res = max(res, w);p[x] = y;}}return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i )scanf("%d%d%d", &edges[i].x, &edges[i].y, &edges[i].w);printf("%d %d\n", n - 1, kruskal());return 0;
}
裸题:1143. 联络员
1143. 联络员 - AcWing题库

添加所有必选的边,维护并查集,然后再对非必选的边做kruskal
#include <iostream>
#include <algorithm>
using namespace std;const int N = 2010, M = 10010;
struct Edge
{int x, y, w;bool operator<(const Edge& e) const {return w < e.w;}
}edges[M];int n, m, cnt;
int p[N];int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int kruskal()
{int res = 0;for (int i = 0; i < cnt; ++ i ){auto t = edges[i];int x = t.x, y = t.y, w = t.w;x = find(x), y = find(y);if (x != y){res += w;p[x] = y;}}return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++ i ) p[i] = i;int t, x, y, d;int res = 0;while ( m -- ){scanf("%d%d%d%d", &t, &x, &y, &d);if (t == 1){x = find(x), y = find(y);if (x != y) p[x] = y;res += d;}else{edges[cnt].x = x, edges[cnt].y = y, edges[cnt].w = d;cnt ++ ;}}sort(edges, edges + cnt);res += kruskal();printf("%d\n", res);return 0;
}
有些麻烦的裸题:1144. 连接格点
1144. 连接格点 - AcWing题库
点阵为图中的点,将二维坐标转换成一维,作为点的编号
添加已有连线后,做kruskal即可
#include <iostream>
#include <algorithm>
using namespace std;const int N = 1010;
struct Edge
{int x, y, w;bool operator<(const Edge& e) const {return w < e.w;}
}edges[2 * N * N];int n, m, cnt = 1;
int p[N * N];
int g[N][N]; // 二维到一维
int dx[3] = { 0, 1, 0 }, dy[3] = { 0, 0, 1 };int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int kruskal()
{int res = 0;for (int i = 0; i < cnt; ++ i ){auto t = edges[i];int x = t.x, y = t.y, w = t.w;x = find(x), y = find(y);if (x != y){res += w;p[x] = y;}}return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++ i )for (int j = 1; j <= m; ++ j )g[i][j] = cnt ++ ;for (int i = 1; i < cnt; ++ i ) p[i] = i;int x1, x2, y1, y2;while (~scanf("%d%d%d%d", &x1, &y1, &x2, &y2)){int x = g[x1][y1], y = g[x2][y2];x = find(x), y = find(y);if (x != y) p[x] = y;}cnt = 0;for (int i = 1; i <= n; ++ i )for (int j = 1; j <= m; ++ j )for (int k = 1; k <= 2; ++ k ){int a = i + dx[k], b = j + dy[k];if (a >= 1 && a <= n && b >= 1 && b <= m){int x = g[i][j], y = g[a][b];edges[cnt ++ ] = { x, y, k };}}sort(edges, edges + cnt);printf("%d\n", kruskal());return 0;
}
debug:n * m的矩阵中,相邻两点之间存在一条边,那么矩阵中的边数应该为m(n-1) + n(m-1),大概就是2 * n * n,数组开小了导致SF
尽量不要在for循环中定义除了循环变量之外的变量

需要注意的是,200万条边进行排序会消耗很多时间,由于边的权值只有1和2,所以可以先添加权值为1的边,再添加权值为2的边
相关文章:

第三章 图论 No.4最小生成树的简单应用
文章目录 裸题:1140. 最短网络裸题:1141. 局域网裸题:1142. 繁忙的都市裸题:1143. 联络员有些麻烦的裸题:1144. 连接格点 存在边权为负的情况下,无法求最小生成树 裸题:1140. 最短网络 1140. 最…...

微服务-nacos配置管理
Nacos配置管理 统一配置管理:一次配置更改并支持热更新。将核心配置存储到配置管理服务,当微服务启动时会自动读取配置管理服务中的配置信息并结合本地配置启动。当配置改动时,配置管理服务会自动通知微服务,微服务读取新配置并自…...

【开发问题】flink的sql任务,用命令行执行
flink-sql 命令行flink-sql的客户端sql文件地址sql的内容 命令行 /mnt/flink/flink-1.17.1/bin/sql-client.sh embedded -f /mnt/flink/flink-1.17.1/examples/sql/oracle2Oracle flink-sql的客户端 /mnt/flink/flink-1.17.1/bin/sql-client.shsql文件地址 /mnt/flink/flink-1…...
Git常见问题
git clone 提示OpenSSL SSL_read git clone 时提示Connection was reset, errno 10054类错误 fatal: unable to acce ss https://github.com/fex-team/ueditor.git/: OpenSSL SSL_read: Connection was reset, errno 10054 备注:以下方法只是归纳整理,…...

Android如何实现开机自启
开机自启有很多种办法,下面用广播的方式实现。 1、首先先创建广播,开机代码 /*** Created by Forrest.* User: Administrator* Date: 2023/3/6* Description:*/ public class BootCompleteReceiver extends BroadcastReceiver {Overridepublic void on…...

Java数组实现的简单点名器
Java数组实现的简单点名器 需求分析代码实现小结Time 需求分析 Java数组实现的简单点名器 用数组将名单存储,然后调用Random函数取随机数实现随机点名。 代码实现 import java.util.Random;public class DianMingDemo {public static void main(String[] args) {//…...

百度UEditor编辑器如何关闭抓取远程图片功能
百度UEditor编辑器如何关闭抓取远程图片功能 这个坑娘的功能,开始时居然不知道如何触发,以为有个按钮,点击一下触发,翻阅了文档,没有发现,然后再网络上看到原来是复制粘贴非白名单内的图片到编辑框时触发&a…...

网站无法访问的常见原因
有多种问题可能会阻止用户访问您的网站。本文将解决无法访问网站,且没有错误消息指示确切问题的情况,希望对您有所帮助。 无法访问网站的常见原因有: (1)DNS 设置不正确。 (2)域名已过期。 (3)空白或没有索引文件。 (4)网络连接问题。 DNS 设…...
(树) 剑指 Offer 34. 二叉树中和为某一值的路径 ——【Leetcode每日一题】
❓ 剑指 Offer 34. 二叉树中和为某一值的路径 难度:中等 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:…...

HDFS集群滚动升级以及回滚相关
HDFS集群滚动升级以及回滚相关 介绍不停机滚动升级非联邦HA集群联邦HA集群 停机升级--非HA集群HDFS集群降级和回滚异同点共同点不同点 HA集群降级(downgrade)注意事项 集群回滚操作 介绍 在hadoop v2中,HDFS支持namenode高可用(H…...
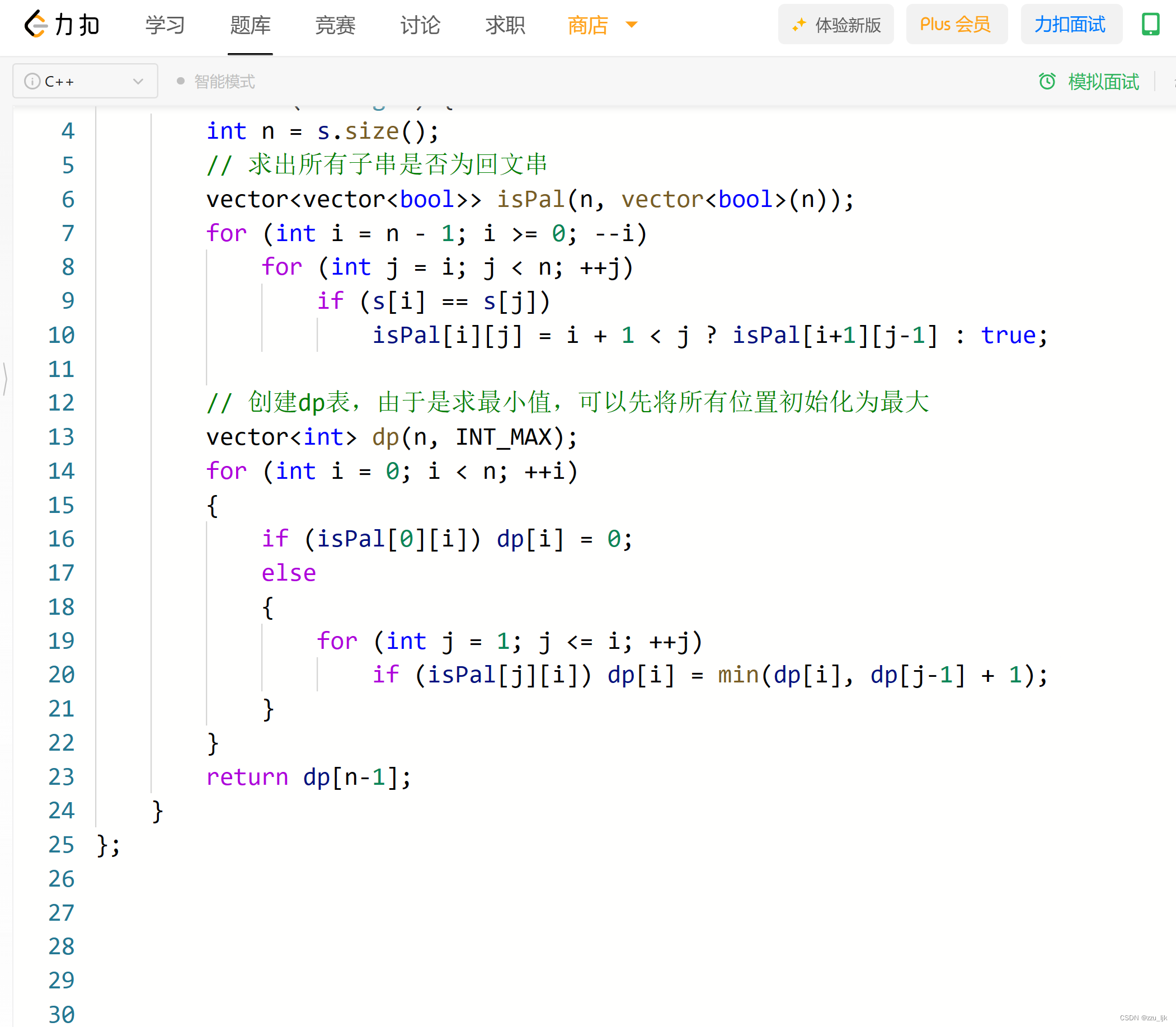
【LeetCode】094. 分割回文串II
文章目录 1. 解题思路1.1 创建dp表1.2 状态转移方程1.3 提前求出所有子串是否是回文串 2. 整体代码 1. 解题思路 1.1 创建dp表 这道题我们使用动态规划的方法来解,首先创建一个大小为字符串长度的dp表。dp[i] 表示 s[0, i] 的字符串最小划分多少次可以全划分为回文…...
CBCGPRibbon 添加背景图片
resource.h中声明资源的ID:ID_RIBBON_BACKIMAGE rc文件中添加png图片路径: ID_RIBBON_BACKIMAGE PNG DISCARDABLE "res\\bkribbon.png" 代码中添加下测: //添加背景图片 m_wndRibbonBar.SetBackgroundImage(ID_RIB…...

无涯教程-Perl - last 语句函数
当在循环内遇到 last 语句时,循环立即终止,程序控制在循环后的下一条语句处恢复。您可以为LABEL提供最后一个语句,其中LABEL是循环的标签。 last 语句可以在嵌套循环内使用,如果未指定LABEL,则该语句将适用于最近的循环…...

网络安全 Day13-Linux三剑客awk知识
Linux三剑客awk知识 1. awk 介绍2. awk 语法3. 练习 1. awk 介绍 awk 是一门语言, 也是一个命令,Linux 有三剑客命令: grep/sed/awk三剑客的特长 grep 过滤内容sed 取行awk 取列 2. awk 语法 取列 取第一列文件($1): awk {print $1} 文件指定分隔符为文件: awk -F "指…...
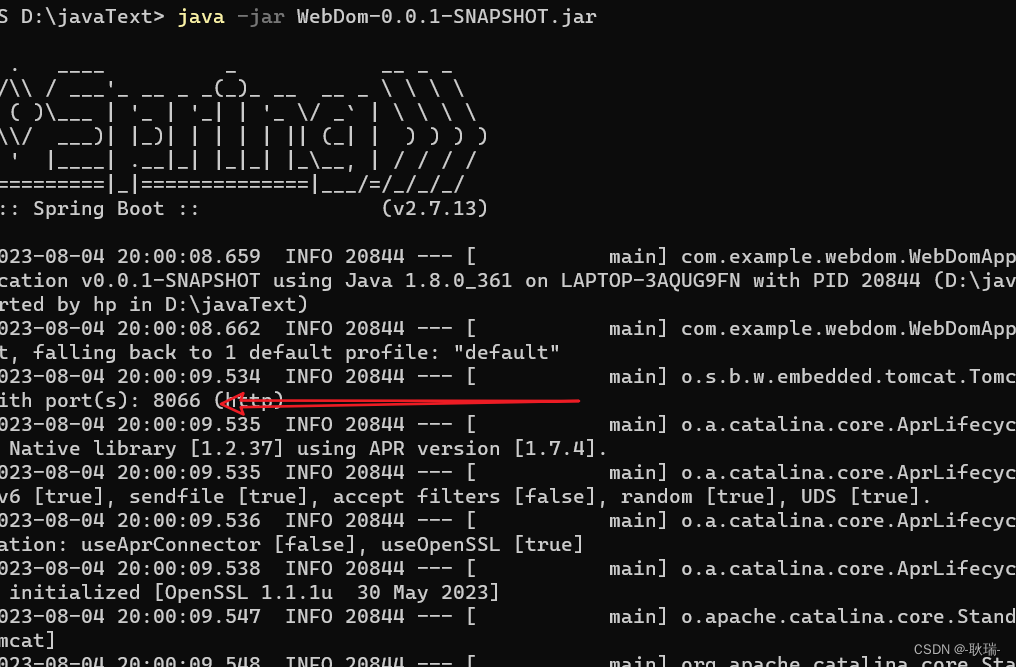
java讲解Spring Boot配置文件级别 相互覆盖关系 解决一方不愿意给数据库密码 一方不愿意给源码时 数据库配置问题
前面 我们讲过Spring Boot 修改临时变量的方式 但另一个场景 就是 我们 在本地开发环境 用的是一个配置 但如果项目经理上线 他想改这些配置 怎么弄呢 特别是数据库之类的配置 很多线上是不太一样的 那么 我们先看一个比较基本的方法 在配置文件的同目录下创建一个目录 叫 con…...

点击表格行高亮
css中三元表达式 :class"[activeIndex index ? color : , item]"点击行高亮 <div click"actvied(index)" :class"[activeIndex index ? color : , item]"v-for"(item, index) in tableData" :key"index">{{ item…...
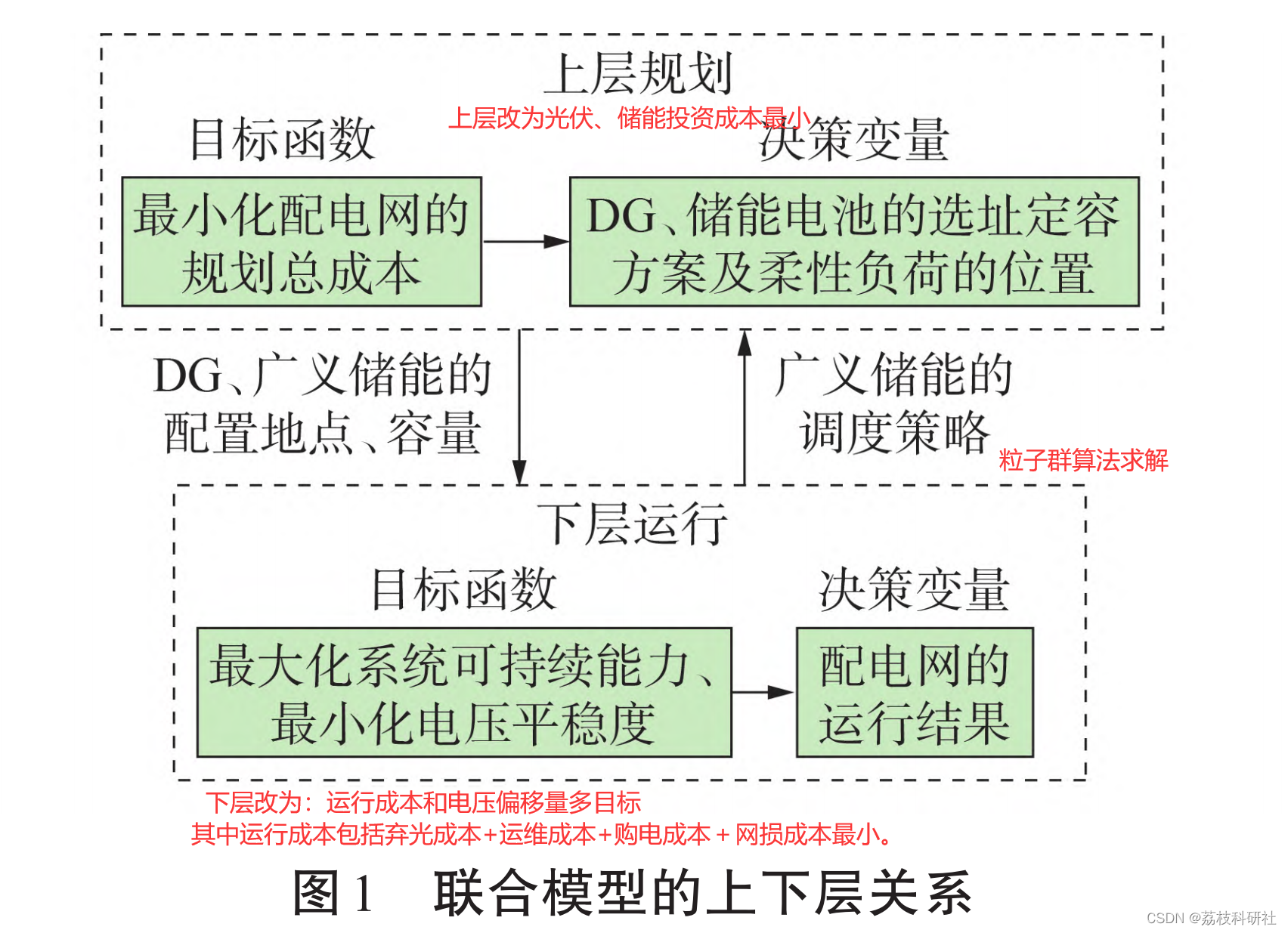
基于粒子群优化算法的配电网光伏储能双层优化配置模型[IEEE33节点](选址定容)(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码、数据、讲解 💥1 概述 由于能源的日益匮乏,电力需求的不断增长等,配电网中分布式能源渗透率不断提高,且逐渐向主动配电网方…...
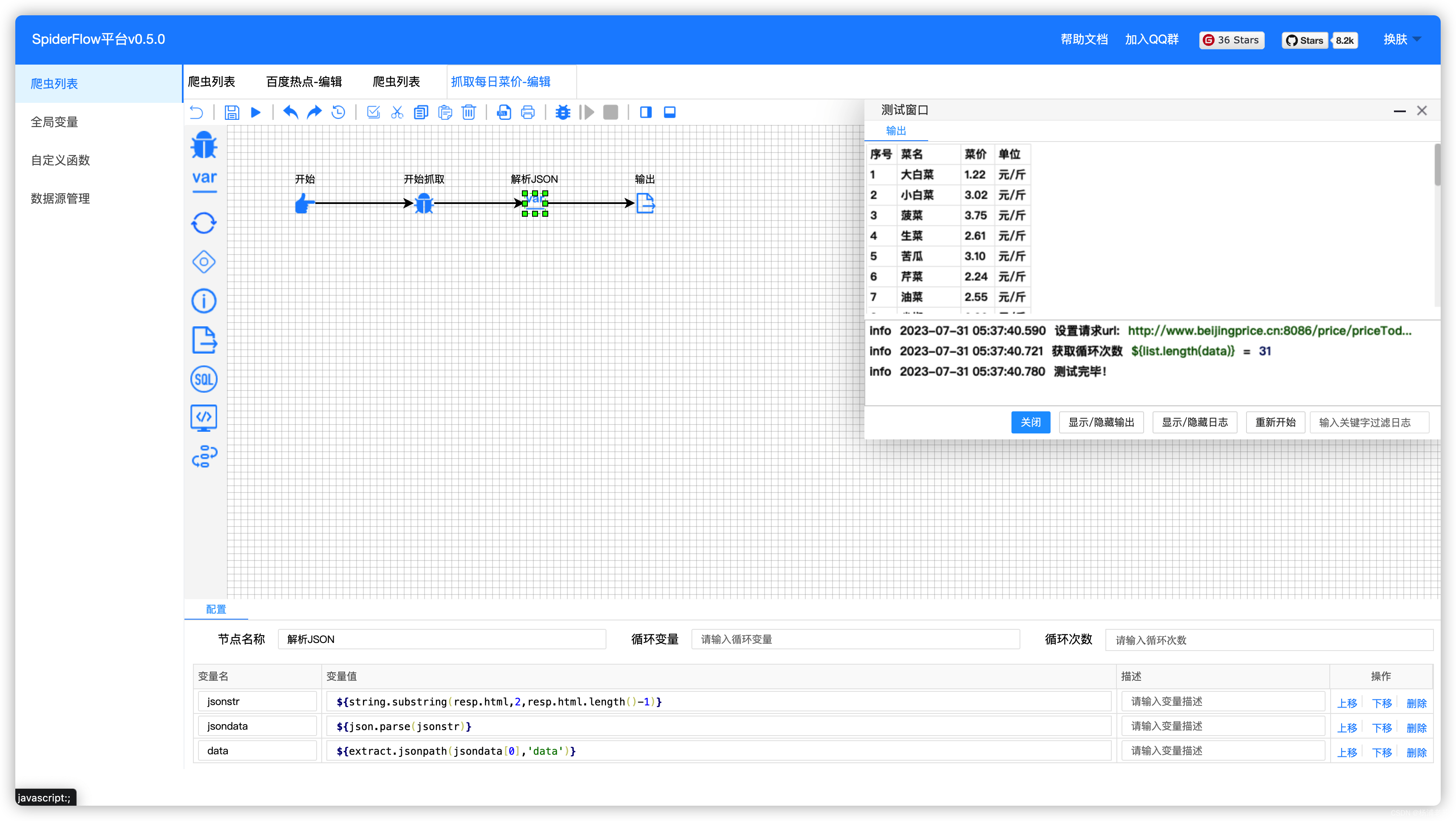
零代码爬虫平台SpiderFlow的安装
什么是 Spider Flow ? Spider Flow 是一个高度灵活可配置的爬虫平台,用户无需编写代码,以流程图的方式,即可实现爬虫。该工具支持多数据源、自动保存至数据库、任务监控、抓取 JS 动态渲染页面、插件扩展(OCR 识别、邮…...

Java 与其他编程语言:比较分析
Java 擅长可移植性和可靠性,Python 擅长通用性和简单性,JavaScript 擅长 Web 开发,C 擅长性能,Go 擅长效率。 在广阔的软件开发世界中,选择正确的编程语言对于任何项目的成功都至关重要。Java 是一种以其多功能性和可移…...
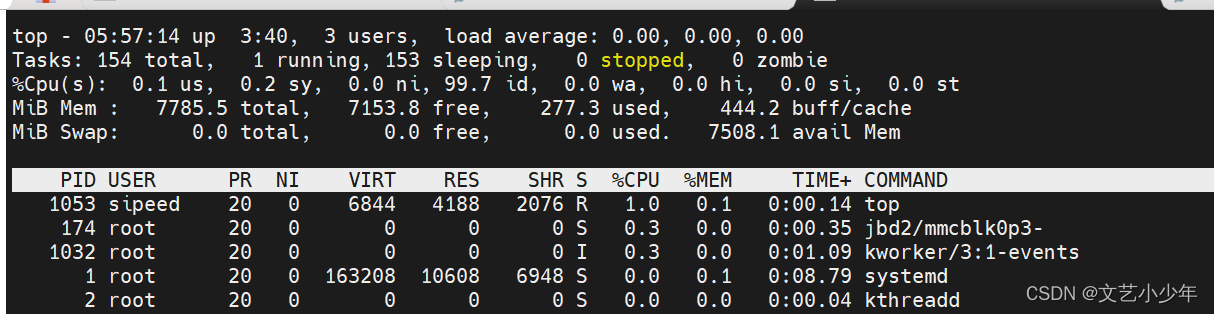
Linux性能分析工具介绍(二)--内存、进程、磁盘、IO分析
目录 一、引言 二、Linux性能分析工具介绍 ------>2.1、进程 ------>2.2、内存 ------>2.3、磁盘 ------>2.4、IO 一、引言 本章从内存、IO、进程的角度,分析linux系统的性能 二、Linux性能分析工具介绍 2.1、进程 2.1.1、top top命令可以动态查看进程…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
