机器学习-特征选择:如何使用Lassco回归精确选择最佳特征?
一、引言
特征选择在机器学习领域中扮演着至关重要的角色,它能够从原始数据中选择最具信息量的特征,提高模型性能、减少过拟合,并加快模型训练和预测的速度。在大规模数据集和高维数据中,特征选择尤为重要,因为不必要的特征会增加计算复杂性并引入冗余信息。
Lasso回归是一种强有力的特征选择方法,通过引入L1正则化来推动部分特征系数稀疏化。相比于其他方法,Lasso回归具有良好的解释性和可解释性,能够自动选择与目标变量相关的重要特征,同时将不相关或冗余特征的系数置零。这使得Lasso回归成为特征选择和维度约简的首选方法。
本文旨在介绍Lasso回归在精确特征选择中的应用。首先,我们将探讨特征选择的重要性,包括如何提高模型性能和降低计算成本。接着,我们将深入解析Lasso回归的原理和算法,并说明其在特征选择中的优势。为了支撑我们的观点,我们将引用相关文献提供的实证结果和案例分析。
二、Lasso回归简介
2.1 Lasso回归的基本原理
Lasso回归,也称为最小绝对收缩和选择算子回归,是一种线性回归方法。其基本原理是在普通最小二乘法的基础上,引入L1正则化项,通过最小化目标函数来实现模型的特征选择和系数稀疏化。
Lasso回归的目标函数如下所示: minimize ||Y - Xβ||^2 + λ||β||₁ 其中,Y是观测值向量,X是特征矩阵,β是待估计的回归系数向量,λ是控制正则化强度的超参数。
L1正则化项λ||β||₁在目标函数中起到了关键作用。它引入了稀疏性,即使得一些特征的系数被压缩为零,从而实现了自动的特征选择。因此,Lasso回归不仅可以进行预测,还可以识别出对目标变量有重要影响的特征。
2.2 Lasso回归与普通最小二乘法区别
Lasso回归与普通最小二乘法之间存在着几个重要的区别。
-
首先,Lasso回归通过引入L1正则化项,使得部分特征的系数变为零。这种特性使得Lasso回归能够实现特征选择,从而减少了模型的复杂度和噪声的影响。而普通最小二乘法并没有引入正则化项,无法直接进行特征选择。 -
其次,Lasso回归的估计结果更具有解释性。由于L1正则化的存在,Lasso回归可以将不相关或冗余的特征系数置为零,只保留与目标变量相关的重要特征。这样一来,Lasso回归得到的模型更简洁、更易解释。而普通最小二乘法则会给出所有特征的系数估计值,无法过滤掉不相关特征。 -
此外,Lasso回归适用于高维数据集。在高维情况下,特征的数量远大于样本的数量,Lasso回归能够通过特征选择来缓解维度灾难的问题。而普通最小二乘法在高维数据集中容易出现过拟合的情况。
综上所述,Lasso回归通过引入L1正则化项,实现了特征选择和系数稀疏化,与普通最小二乘法相比,在模型解释性和适应高维数据等方面具有一定的优势。
三、特征选择的方法
3.1 过滤方法
过滤方法是一种常见的特征选择方法,它通过在训练模型之前对特征进行筛选,选择那些与目标变量相关性较高的特征。以下是几种常用的过滤方法:
-
方差阈值:方差阈值方法是通过计算特征在样本中的变化程度来进行特征选择。具体来说,计算每个特征的方差,并将方差低于某个阈值的特征排除。这种方法适用于对离散特征进行选择。 -
互信息:互信息是衡量两个随机变量之间相互依赖程度的度量指标。在特征选择中,可以计算每个特征与目标变量之间的互信息,然后选择互信息高于某个阈值的特征。互信息方法适用于对离散或连续变量之间的关系进行选择。 -
相关性系数:相关性系数是衡量两个变量之间线性相关程度的指标。常用的相关性系数包括皮尔逊相关系数和斯皮尔曼等级相关系数。通过计算每个特征与目标变量之间的相关性系数,可以选择与目标变量具有较高相关性的特征。相关性系数方法适用于对连续变量之间的关系进行选择。
这些过滤方法都是基于统计学原理和度量指标来进行特征选择的,它们简单直观,计算效率高,并且可以帮助筛选出与目标变量相关性较强的特征。但是过滤方法忽略了特征之间的相互作用和非线性关系,可能会无法捕捉到一些重要的特征。因此,在实际应用中,可以结合其他特征选择方法,如包裹方法和嵌入方法,以获得更准确和鲁棒的特征选择结果。
3.2 包装方法
包装方法是一种更为复杂和耗时的特征选择方法,它通过使用某个学习模型来评估特征的重要性,并根据重要性进行特征选择。以下是两种常见的包装方法:
-
递归特征消除(Recursive Feature Elimination, RFE):递归特征消除是一种迭代的特征选择方法。它通过反复训练一个学习模型,并在每次迭代中排除对目标变量影响较小的特征。具体步骤如下:首先,训练一个学习模型,根据特征的重要性进行排序。然后,删除最不重要的特征,重新训练模型,并继续迭代直到达到指定的特征数目或达到停止条件。递归特征消除适用于任何学习模型,并且可以通过交叉验证来选择最佳的特征子集。 -
基于遗传算法的特征选择:基于遗传算法的特征选择是一种优化算法,通过模拟生物进化过程来搜索最佳特征子集。这种方法将特征作为个体,通过交叉、变异和选择等操作来生成新的特征子集,并利用评估函数(如模型准确率)来评估特征子集的质量。遗传算法根据评估函数的反馈进行迭代优化,直到找到最佳的特征子集为止。基于遗传算法的特征选择可以全局搜索特征空间,并且具有较强的鲁棒性和适应性。
包装方法相对于过滤方法更为精确,能够考虑特征之间的相互作用和非线性关系。然而,由于包装方法需要多次训练模型,计算复杂度较高,并且对于大规模数据集可能不太适用。因此,在应用包装方法时需要权衡计算资源和模型性能的平衡。同时,选择合适的学习模型和评估函数也是非常重要的,以确保得到准确和稳定的特征选择结果。
3.3 嵌入方法
嵌入方法是一种将特征选择与模型训练过程相结合的方法,它通过在学习模型中嵌入特征选择来选择最佳的特征子集。以下是一个常见的嵌入方法:
-
基于Lasso回归的特征选择:Lasso(Least Absolute Shrinkage and Selection Operator)回归是一种线性回归的扩展,它利用L1正则化项对模型的系数进行约束,从而实现特征选择。具体来说,Lasso回归通过最小化目标函数,其中包括了平方损失和L1正则化项。在优化过程中,Lasso回归会使得部分特征的系数变为0,从而实现了特征的稀疏性,剔除了对目标变量影响较小的特征。通过调节正则化参数,可以控制特征选择的程度。基于Lasso回归的特征选择适用于线性模型,它能够同时进行特征选择和模型训练,并且能够处理高维数据。
嵌入方法将特征选择与模型训练过程融合在一起,能够自动选择与目标变量相关性较强的特征。相比于过滤方法和包装方法,嵌入方法更加灵活,能够考虑到特征之间的相互作用。然而,嵌入方法通常需要更多的计算资源和时间,并且对于非线性模型可能效果不如包装方法或过滤方法。因此,在选择嵌入方法时,需要根据具体问题和数据集的特点进行权衡和选择合适的方法。
四、Lasso的特征选择流程
-
「数据预处理」:
-
收集并整理原始数据集。 -
处理缺失值、异常值和离群点。 -
对特征进行标准化或归一化,确保它们具有相似的尺度。
-
「划分训练集和测试集」:
-
将数据集划分为训练集和测试集,通常采用交叉验证的方式。
-
「搭建Lasso回归模型」:
-
使用训练集拟合Lasso回归模型。 -
在拟合过程中,通过调节正则化参数来控制特征的稀疏性。可以使用交叉验证或网格搜索等方法找到最佳的正则化参数。
-
「特征系数选择」:
-
根据训练好的Lasso回归模型,获取所有特征的系数。 -
对系数进行排序,按照绝对值从大到小排序。
-
「特征选择」:
-
设置一个阈值,保留系数大于阈值的特征。 -
可以根据先验知识和实际需求来选择阈值,也可以通过交叉验证确定最佳的阈值。
-
「模型评估」:
-
使用保留的特征重新训练Lasso回归模型。 -
使用测试集评估模型的性能,比较选择特征和原始全特征的模型性能。
五、实例演示
5.1 数据集载入
library(survival)
str(gbsg)
结果展示:
> str(gbsg)
'data.frame': 686 obs. of 10 variables:
$ age : int 49 55 56 45 65 48 48 37 67 45 ...
$ meno : int 0 1 1 0 1 0 0 0 1 0 ...
$ size : int 18 20 40 25 30 52 21 20 20 30 ...
$ grade : int 2 3 3 3 2 2 3 2 2 2 ...
$ nodes : int 2 16 3 1 5 11 8 9 1 1 ...
$ pgr : int 0 0 0 0 0 0 0 0 0 0 ...
$ er : int 0 0 0 4 36 0 0 0 0 0 ...
$ hormon : int 0 0 0 0 1 0 0 1 1 0 ...
$ rfstime: int 1838 403 1603 177 1855 842 293 42 564 1093 ...
$ status : Factor w/ 2 levels "0","1": 1 2 1 1 1 2 2 1 2 2 ...
age:患者年龄
meno:更年期状态(0表示未更年期,1表示已更年期)
size:肿瘤大小
grade:肿瘤分级
nodes:受累淋巴结数量
pgr:孕激素受体表达水平
er:雌激素受体表达水平
hormon:激素治疗(0表示否,1表示是)
rfstime:复发或死亡时间(以天为单位)
status:事件状态(0表示被截尾,1表示事件发生)
5.2 Lasso和特征选择
-
「数据预处理」
colSums(is.na(gbsg))
set.seed(1234)
gbsg$status <- as.factor(gbsg$status)
# 拆分训练集和测试集
trainIndex <- sample(1:nrow(gbsg), 0.8 * nrow(gbsg))
train <- gbsg[trainIndex,]
test <- gbsg[-trainIndex,]
-
「搭建Lasso回归模型」
# 安装并加载所需的R包
install.packages("glmnet")
library(glmnet)
x <- as.matrix(train[, c(-1,-11)])
y <- as.numeric(train$status)
# 计算标准化前的均值和标准差
colMeans(x)
apply(x,2,sd)
# 标准化
x = scale(x,center = T,scale = T)
# 构建模型
la_md <- glmnet(x, y, lambda=0.1,
family='gaussian',
intercept = F, alpha=1)
glmnet函数是用于构建弹性网络模型的函数,具体解释如下:
-
x:自变量矩阵,包含训练数据的特征。每一行代表一个样本,每一列代表一个特征。 -
y:因变量向量,包含训练数据的响应变量。 -
lambda:正则化参数,控制模型的复杂度。较大的lambda值会导致更多的系数为0,从而减小模型的复杂度和过拟合的风险。 -
family:指定了回归模型的误差分布。对于高斯分布(正态分布)的响应变量,可以选择'gaussian'。还有其他可选的分布类型,如二项分布('binomial')和泊松分布('poisson')等。 -
intercept:是否包括截距项。设置为TRUE表示包括截距项,设置为FALSE表示不包括截距项。 -
alpha:弹性网络的混合参数,介于0和1之间。当alpha为1时,模型为Lasso回归;当alpha为0时,模型为岭回归。
关于如何设置lambda和alpha,以及family的选择,这需要根据具体问题和数据来进行调整。一般来说:
-
lambda:可以通过交叉验证法(cross-validation)来选择合适的lambda值。函数cv.glmnet可以帮助我们进行交叉验证,选择最优的lambda值。 -
alpha:如果你对注意力集中在少数变量上,倾向于使用Lasso回归,那么可以选择较大的alpha值。如果你更希望模型保留更多有用的变量,可以选择较小的alpha值。 -
family:根据响应变量的性质和概率分布选择合适的误差分布类型。例如,如果响应变量是二分类变量,可以选择二项分布('binomial');如果响应变量是计数数据,可以选择泊松分布('poisson')。多项分布('multinomial')适用于多分类问题。
需要注意的是,这只是一些一般性的指导原则。具体的选择还要考虑数据的特点和分析目标。
-
「Lasso筛选变量动态过程图」
# Lasso筛选变量动态过程图
la.md <- glmnet(x, y, family="gaussian",
intercept = F, alpha=1)
# plot
plot(la.md,xvar = "lambda", label = F)
从图中,我们可以看出,随着lambda增大,各特征相应的也被压缩得更小,而当lambda达到一定值以后,一部分不重要的特征将被压缩为0,代表该变量已被剔除出模型,图中从左至右不断下降的曲线如同被不断增大的lambda一步一步压缩,直到压缩为0。
「对于特征的系数大小」:
-
正的系数表示该特征与响应变量之间存在正相关关系。当特征的取值增加时,响应变量的期望值也会增加。 -
负的系数表示该特征与响应变量之间存在负相关关系。当特征的取值增加时,响应变量的期望值会减少。
「对于特征的非零系数个数」:
-
当某个特征的非零系数个数为正数时,表示该特征在模型中被选择为重要特征,并且对预测结果有显著影响。 -
当某个特征的非零系数个数为零时,表示该特征在模型中被排除或被忽略,对预测结果没有显著影响。
需要明确的是,特征的系数大小和非零系数个数仅反映特征与响应变量之间的关系,并不能直接推断特征的实际影响或取值。具体特征对应的实际取值以及与响应变量之间的关系,还需要根据具体问题和数据背景进行进一步分析和解释。
-
「计算出合适的lambda值」
可以通过交叉验证法(cross-validation)来选择合适的lambda值。函数cv.glmnet可以帮助我们进行交叉验证,选择最优的lambda值.
mod_cv <- cv.glmnet(x=x, y=y, family="gaussian", # 默认nfolds = 10
intercept = F, alpha=1)
plot(mod_cv)
# 最小误差对应的lambda和最小误差
print(paste(mod_cv$lambda.min,
log(mod_cv$lambda.min)))
print(paste(mod_cv$lambda.1se,
log(mod_cv$lambda.1se)))
# 这里我们以lambda.min为最优 λ
best_lambda <- mod_cv$lambda.min
best_lambda
结果显示:
> print(paste(mod_cv$lambda.min,
+ log(mod_cv$lambda.min)))
[1] "0.093983735301881 -2.36463354038672"
> print(paste(mod_cv$lambda.1se,
+ log(mod_cv$lambda.1se)))
[1] "0.217114618245629 -1.52732987020707"
通过交叉验证,我们可以选择平均误差最小的那个λ,即mod_cv lambda.1se。从图中可以看出,λ在-3和-2之间最低,大概是-2.3左右的样子误差最小。然后从打印出的最佳lambda是0.09398374。
-
「特征选择」
best_model <- glmnet(x, y, alpha = 1, lambda = best_lambda)
coef(best_model)
结果展示:
10 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 1.4489051
age .
meno .
size .
grade .
nodes .
pgr .
er .
hormon .
rfstime -0.1232434
如变量没有显示系数,即lasso回归收缩系数为零。这意味着它完全被排除在模型之外,因为它的影响力不够。系数非0的变量即为我们筛选的重要特征。
-
「使用最终模型进行预测」
x_test <- as.matrix(test[, c(-1,-11)])
y_test <- as.numeric(test$status)
# 标准化
x_test = scale(x_test,center = T,scale = T)
#使用 lasso 回归模型预测
y_predicted <- predict(best_model, s = best_lambda, newx = x_test)
sst <- sum((y_test - mean(y_test))^2)
sse <- sum((y_predicted - y_test)^2)
rsq <- 1 - sse/sst
rsq
结果展示:
> rsq
[1] 0.1607887
rsq即是R²:
-
当R²接近0时,模型无法解释响应变量的变异性,拟合程度较差,意味着模型对数据的解释能力很弱。 -
当R²接近0.5时,模型能够解释部分响应变量的变异性,但还有很大一部分变异不能被模型解释,拟合程度一般。 -
R²大于0.6或者0.7可以作为一个相对较好的指标,在医学领域,但还需要综合考虑其他因素来评估模型的优劣 -
当R²为1时,表示该预测模型完全解释了响应变量的变异性,即模型能够完美拟合数据
这里解释一下为什么这次的R²只有0.16,远远低于0.5,更是低于医学可接受的值,我使用的数据是二分类数据,即只有0和1是离散型变量,不是连续型的数值。所以使用R²来评价是不合理的。所以这个偏差是合理的。
六、总结
6.1 适用于连续性因子变量
Lasso回归是一种用于特征选择和预测建模的线性回归方法,通常用于连续型的数值响应变量。对于因子类型的离散响应变量,Lasso回归通常不直接适用。
对于因子类型的响应变量,通常需要使用适合离散型数据的回归模型,例如逻辑回归(Logistic Regression)或多项式回归(Multinomial Regression)。这些模型可以应用于分类问题或多类别预测问题。
逻辑回归(Logistic Regression)用于二分类问题,将因子型的响应变量映射为概率值,表示某个类别的概率。多项式回归(Multinomial Regression)则用于多分类问题,将因子型的响应变量映射为多个类别的概率分布。
需要注意的是,无论是使用Lasso回归还是其他回归方法,对于因子类型的响应变量,都需要进行适当的编码和转换,将因子变量映射为数值型变量,以便模型的计算和分析。
6.2 如何使二分类0和1如何使用Lasso回归?
如果因子类型的响应变量只有两个取值(0和1),可以将问题看作是二分类问题。在这种情况下,Lasso回归可以被用于选择与响应变量相关性最强的特征,并建立一个预测模型。
在使用Lasso回归时,需要对因子型的响应变量进行适当的编码。一种常见的编码方法是使用虚拟变量(Dummy Variable)编码。将因子型的响应变量转化为两个虚拟变量,如0表示一个类别,1表示另一个类别,然后使用Lasso回归进行建模。
虽然Lasso回归原本是用于处理连续型的数值响应变量,但通过将因子型的响应变量进行适当的编码,我们可以将其扩展到处理二分类问题。这是因为Lasso回归对特征的选择性质仍然适用。
需要注意的是,在使用Lasso回归进行二分类建模时,我们通常使用的评估指标是准确率、精确率、召回率或F1分数等,而非均方误差(Mean Squared Error)等用于度量连续型响应变量的指标。
这里是不是解释了刚才我们计算出的R²的偏低情况。如果想了解如何使用Lasso回归如何对离散型的因子变量进行特征筛选,欢迎关注和私信我,我们一起讨论学习。原创不易,如果觉得写的还行的话,请留下您的赞和再看,谢谢!
*「未经许可,不得以任何方式复制或抄袭本篇文章之部分或全部内容。版权所有,侵权必究。」
相关文章:
机器学习-特征选择:如何使用Lassco回归精确选择最佳特征?
一、引言 特征选择在机器学习领域中扮演着至关重要的角色,它能够从原始数据中选择最具信息量的特征,提高模型性能、减少过拟合,并加快模型训练和预测的速度。在大规模数据集和高维数据中,特征选择尤为重要,因为不必要的…...
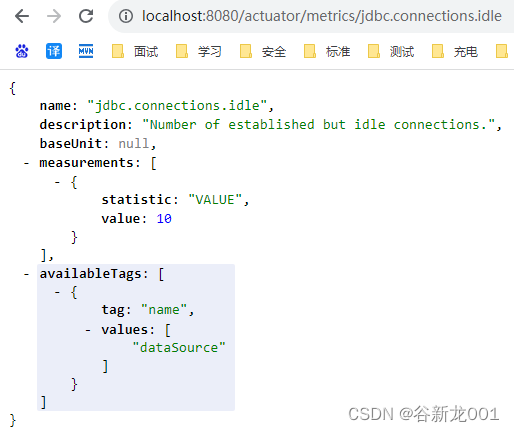
SpringBoot之Actuator基本使用
SpringBoot之Actuator基本使用 引入分类常用接口含义healthbeansconditionsheapdumpmappingsthreaddumploggersmetrics 引入 <!-- actuator start--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter…...
)
排序算法(一)
1.冒泡排序-Bubble Sort 1.算法原理 依次比较相邻的两个元素,若按照从小到大的顺序,则将相邻元素中较大的一个放在后面;然后对每一对相邻元素都做这种比较,序列的最后一个元素就是最大的数; 2.算法复杂度 时间复杂度…...

Centos虚拟机忘记密码-修改密码
1.重启系统 2.在这个选择界面,按e建 3.找到如下位置,插入init/bin/sh 4.填写完成后按Ctrlx引导启动 5.输入mount -o remount, rw / (注意空格) 6.重置密码 出现以下为重置成功 7.执行touch /.autorelabel 8.退出exec /sbin/init 9.输入你的新密…...

Shell 分析服务器日志常用命令
1、查看有多少个IP访问: 日志文件的第一列是IP地址 awk {print $1} log_file|sort|uniq|wc -l2、查看某一个页面被访问的次数: grep "/index.php" log_file | wc -l3、查看每一个IP访问了多少个页面: awk {S[$1]} END {for (a i…...

mysql8配置binlog日志skip-log-bin,开启、关闭binlog,清理binlog日志文件
1.概要说明 binlog 就是binary log,二进制日志文件,这个文件记录了MySQL所有的DML操作。通过binlog日志我们可以做数据恢复,增量备份,主主复制和主从复制等等。对于开发者可能对binlog并不怎么关注,但是对于运维或者架…...

机器学习:训练集与测试集分割train_test_split
1 引言 在使用机器学习训练模型算法的过程中,为提高模型的泛化能力、防止过拟合等目的,需要将整体数据划分为训练集和测试集两部分,训练集用于模型训练,测试集用于模型的验证。此时,使用train_test_split函数可便捷高…...
简单介绍淘宝API功能接口作用)
淘宝API开发(一)简单介绍淘宝API功能接口作用
前一阵子按照上级指示,根据淘宝API开发符合自已应用的系统,比如批量上传,批量修改名称,价格等功能什么的,在此就将我的开发历程写一写,为自己前段时间的工作做个总结。 淘宝开发平台(淘宝网 - 淘ÿ…...

Redis相关面试题
Redis的使用场景 根据自己简历上的业务进行回答 缓存 穿透、击穿、雪崩、双写一致、持久化、数据过期、淘汰策略 分布式锁 setnx redisson 缓存穿透:查询一个不存在的数据,数据库查不到数据也不会直接写入缓存,就会导致每次请求都查询数据库…...

数据库简介
1、数据库安装: rpm (redhat package manager) 也是个包管理工具: rpm -ivh 安装 rpm -e 表示卸载,卸载的时候有可能出现依赖的问题,可以用 --nodeps 忽略依赖卸载。 rpm -qa 搜索系统中安装的rpm的应用。 如果使用离线包,安装顺序不要乱。 m…...

腾讯云国际轻量应用服务器怎么使用呢?
腾讯云国际轻量应用服务器怎么使用呢?下面一起来了解一下: 1. 熟悉轻量应用服务器基础知识 ①什么是轻量应用服务器 TencentCloud Lighthouse? ②轻量应用服务器与云服务器 CVM 的区别是什么? ③为什么选择轻量应用服务器…...

arm环境cloudstack在vpc下创建虚拟机失败
一、环境说明 操作系统:openEuler 22.03CPU:Kunpeng-920,arm v8cloudstack:4.18libvirtd:6.2.0 二、问题描述 在UI上创建VPC后,平台会同时创建一个virtual router,此时virtual router有两个网…...
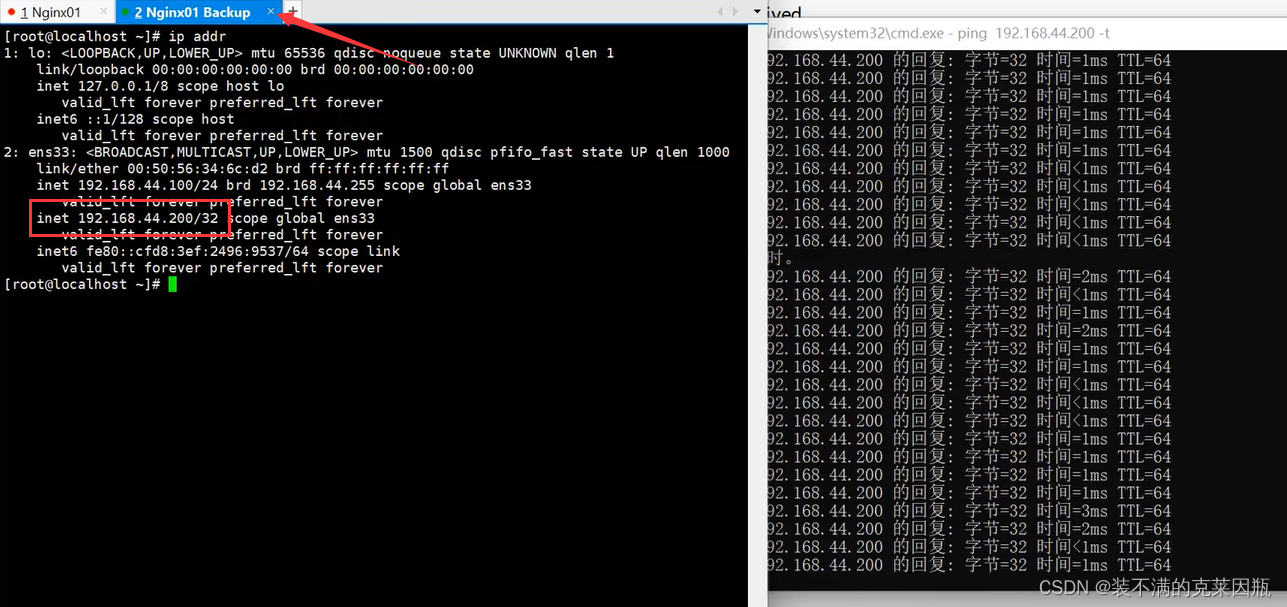
Linux上安装Keepalived,多台Nginx配置Keepalived(保姆级教程)
目录 一、yum安装 第一步:下载 第二步:编辑Keepalived配置文件(第一台) 第三步:编辑Keepalived配置文件(第二台) 第四步:我们在本机利用cmd ping一下 一、yum安装 第一步&…...

centos7 ‘xxx‘ is not in the sudoers file...
如题 执行命令输入密码后时报错: [sudo] password for admin (我的账户)原因,当前用户还没有加入到root的配置文件中。 解决 vim打开配置文件,如下: #切换到root用户 su #编辑配置文件 vim /etc/sudoe…...

Zebec Payroll :计划推出 WageLink On-Demand Pay,进军薪酬发放领域
“Zebec Protocol 生态旨以 Web3 的方式建立全新的公平秩序,基于其流支付体系构建的薪酬支付板块,就是解决问题的一把利刃”...

【2023】字节跳动 10 日心动计划——第三关
目录 1. 最长有效括号2. 有序数组的平方 1. 最长有效括号 🔗 原题链接:32. 最长有效括号 类似于有效的括号,考虑用栈来解决。 具体来讲,我们始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」&…...
【无网络】win10更新后无法联网,有线无线都无法连接,且打开网络与Internet闪退
win10更新后无法联网,有线无线都无法连接,且打开网络与Internet闪退 法1 重新配置网络法2 更新驱动法3 修改注册表编辑器法4 重装系统 自从昨晚点了更新与重启后,今天电脑就再也不听话了,变着花样地连不上网。 检查路由器…...

HTML <script> 标签
实例 在 HTML 页面中插入一段 JavaScript: <script type="text/javascript"> document.write("Hello World!") </script>(在本页底部可以找到更多实例) 定义和用法 <script> 标签用于定义客户端脚本,比如 JavaScript。 script …...

FPGA----UltraScale+系列的PS侧与PL侧通过AXI-HP交互(全网唯一最详)附带AXI4协议校验IP使用方法
1、之前写过一篇关于ZYNQ系列通用的PS侧与PL侧通过AXI-HP通道的文档,下面是链接。 FPGA----ZCU106基于axi-hp通道的pl与ps数据交互(全网唯一最详)_zcu106调试_发光的沙子的博客-CSDN博客大家好,今天给大家带来的内容是࿰…...

Unity小游戏——迷你拼图
游戏展示 拼图演示 资源: 链接:https://pan.baidu.com/s/1BGeSmRCO_WZRUyl3MxefGw 提取码:0n4a 一、玩法介绍 排列拼图碎片,拼出最后的图案。可以点住碎片的任意位置拖动;点击"重来"按钮,可以…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
