第六章 支持向量机
文章目录
- 支持向量机
- 间隔和支持向量
- 对偶问题
- 问题推导
- SMO
- 核函数
- 实验
支持向量机
⽀持向量机(Support Vector Machines,SVM)
- 优点:泛化错误率低,计算开销不⼤,结果易解释。
- 缺点:对参数调节和核函数的选择敏感,原始分类器不加修改仅适⽤于处理⼆类问题。
适⽤数据类型:数值型和标称型数据。
间隔和支持向量
假设数据是可分的,该算法就是为了找到一个超平面将两者分开
⽀持向量(support vector)就是离分隔超平⾯最近的那些点。接下来要试着最⼤化⽀持向量到分隔⾯的距离,需要找到此问题的优化求解⽅法
分割超平面的方程为 w T x + b = 0 w^Tx+b=0 wTx+b=0
计算点A到分割超平面的距离 r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r=\cfrac{|w^Tx+b|}{||w||} r=∣∣w∣∣∣wTx+b∣
为了方便计算,类别标签label使用+1和-1: l a b e l ∗ w T x + b \mathrm{label}*w^Tx+b label∗wTx+b可以同号。
现在的目标就是找出分类器定义中的w和b。为此要找到具有最小间隔的数据点,而这些数据点也就是前面提到的支持向量。对该间隔最大化: arg max w , b { min n ( l a b e l ⋅ ( w T x + b ) ) ⋅ 1 ∥ w ∥ } \arg\max_{w,b}\left\{\min_n(\mathrm{label}\cdot(w^\mathrm{T}x+b))\cdot\frac1{\|w\|}\right\} argw,bmax{nmin(label⋅(wTx+b))⋅∥w∥1}
为了简化问题,令支持向量到超平面距离为1: r ≥ 1 r\geq 1 r≥1 ,则有 { w T x i + b ⩾ + 1 , y i = + 1 w T x i + b ⩽ − 1 , y i = − 1 \left\{\begin{array}{ll}\boldsymbol{w^\mathrm{T}}\boldsymbol{x_i}+b\geqslant+1,&y_i=+1\\\boldsymbol{w^\mathrm{T}}\boldsymbol{x_i}+b\leqslant-1,&y_i=-1\end{array}\right. {wTxi+b⩾+1,wTxi+b⩽−1,yi=+1yi=−1
两个一类支持向量到超平面的距离之和为 γ = 2 ∣ ∣ w ∣ ∣ \gamma=\frac2{||\boldsymbol{w}||} γ=∣∣w∣∣2
要使得间隔最大 max 2 ∣ ∣ w ∣ ∣ \max\frac2{||w||} max∣∣w∣∣2,等价于 min 1 2 ∣ ∣ w ∣ ∣ 2 \min\frac12||w||^2 min21∣∣w∣∣2,即 min 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i + b ) ≥ 1 \min\frac{1}{2}||w||^2\quad s.t.\quad y_i(w^Tx_i+b)\geq 1 min21∣∣w∣∣2s.t.yi(wTxi+b)≥1
对偶问题
问题推导
回顾一下高等数学中约束极值的求法:
z = f ( x , y ) z=f(x,y) z=f(x,y)在条件 ψ ( x , y ) = 0 \psi(x,y)=0 ψ(x,y)=0下取得极值,求极值:
- 构造拉格朗日函数 F ( x , y , λ ) = f ( x , y ) + λ ψ ( x , y ) F(x,y,\lambda)=f(x,y)+\lambda\psi(x,y) F(x,y,λ)=f(x,y)+λψ(x,y)
- 令 { f x ′ ( x , y ) + λ ψ x ′ ( x , y ) = 0 f y ′ ( x , y ) + λ ψ y ′ ( x , y ) = 0 ψ ( x , y ) = 0 \left\{\begin{aligned} &f'_x(x,y)+\lambda\psi'_x(x,y)=0\\ &f'_y(x,y)+\lambda\psi'_y(x,y)=0\\ &\psi(x,y)=0\\ \end{aligned}\right. ⎩ ⎨ ⎧fx′(x,y)+λψx′(x,y)=0fy′(x,y)+λψy′(x,y)=0ψ(x,y)=0
- 将求出的点带入
现问题:求 1 2 ∣ ∣ w ∣ ∣ 2 \frac12||w||^2 21∣∣w∣∣2在 y i ( w T x i + b ) ≥ 1 y_i(w^Tx_i+b)\geq 1 yi(wTxi+b)≥1条件下的最小值
解决方法:引入拉格朗日乘子 α i ⩾ 0 \alpha_{i}\geqslant0 αi⩾0,构造拉格朗日函数 L ( w , b , α ) = 1 2 ∥ w ∥ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) L(\boldsymbol{w},b,\boldsymbol{\alpha})=\frac12\left.\|\boldsymbol{w}\|^2+\sum_{i=1}^m\alpha_i\left(1-y_i(\boldsymbol{w}^\mathrm{T}\boldsymbol{x}_i+b)\right)\right. L(w,b,α)=21∥w∥2+i=1∑mαi(1−yi(wTxi+b))
其中 α = ( α 1 ; α 2 ; … ; α m ) \boldsymbol{\alpha}=(\alpha_{1};\alpha_{2};\ldots;\alpha_{m}) α=(α1;α2;…;αm) ,对w和b偏导为0可得: w = ∑ i = 1 m α i y i x i , 0 = ∑ i = 1 m α i y i . \begin{aligned}\boldsymbol{w}&=\sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i,\\0&=\sum_{i=1}^m\alpha_iy_i.\end{aligned} w0=i=1∑mαiyixi,=i=1∑mαiyi.
联立后,可解得对偶问题 max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j s . t . ∑ i = 1 m α i y i = 0 , α i ⩾ 0 , i = 1 , 2 , … , m . \max_{\boldsymbol{\alpha}}\sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^\mathrm{T}\boldsymbol{x}_j\\ \begin{aligned}\mathrm{s.t.}\quad&\sum_{i=1}^m\alpha_iy_i=0, \\ &\alpha_i\geqslant0,\quad i=1,2,\ldots,m. \end{aligned} αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxjs.t.i=1∑mαiyi=0,αi⩾0,i=1,2,…,m.
最后模型为 f ( x ) = w T x + b = ∑ i = 1 m α i y i x i T x + b . s . t . { α i ⩾ 0 ; y i f ( x i ) − 1 ⩾ 0 ; α i ( y i f ( x i ) − 1 ) = 0. \begin{aligned}f(\boldsymbol{x})&=\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b\\&=\sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i^\mathrm{T}\boldsymbol{x}+b.\end{aligned} \\\mathrm{s.t.}\left\{\begin{array}{l}\alpha_i\geqslant0;\\y_if(\boldsymbol{x}_i)-1\geqslant0;\\\alpha_i\left(y_if(\boldsymbol{x}_i)-1\right)=0.\end{array}\right. f(x)=wTx+b=i=1∑mαiyixiTx+b.s.t.⎩ ⎨ ⎧αi⩾0;yif(xi)−1⩾0;αi(yif(xi)−1)=0.
SMO
推导的式子已经得到了,但是如何求解这些参数?SMO是其中一个高效算法的代表。
SMO的基本思路是先固定 α i \alpha_i αi之外的所有参数,然后求 α i \alpha_i αi上的极值.由于存在约束 ∑ i = 1 m α i y i = 0 \sum_{i=1}^m\alpha_iy_i=0 ∑i=1mαiyi=0,若固定 α i \alpha_i αi之外的其他变量,则 α i \alpha_i αi可由其他变量导出.于是,SMO每次选择两个变量 α i \alpha_i αi和 α j \alpha_j αj,并固定其他参数.这样,在参数初始化后,SMO不断执行如下两个步骤直至收敛:
- 选取一对需更新的变量 α i \alpha_i αi和 α j \alpha_j αj;
- 固定 α i \alpha_i αi和 α j \alpha_j αj以外的参数,求解式获得更新后的 α i \alpha_i αi和 α j \alpha_j αj.
则约束变为 α i y i + α j y j = c , α i ⩾ 0 , α j ⩾ 0 c = − ∑ k ≠ i , j α k y k \begin{aligned}\alpha_iy_i+\alpha_jy_j&=c,\alpha_i\geqslant0,\alpha_j\geqslant0\\\\c&=-\sum_{k\neq i,j}\alpha_ky_k\end{aligned} αiyi+αjyjc=c,αi⩾0,αj⩾0=−k=i,j∑αkyk
确定偏移项b的时候,现实任务中常采用一种更鲁棒的做法:使用所有支持向量求解的平均值(支持向量下标集 S = { i ∣ α i > 0 , i = 1 , 2 , … , m } S=\{i\mid\alpha_{i}>0,i=1,2,\ldots,m\} S={i∣αi>0,i=1,2,…,m}): b = 1 ∣ S ∣ ∑ s ∈ S ( y s − ∑ i ∈ S α i y i x i T x s ) b=\frac{1}{|S|}\sum_{s\in S}\left(y_s-\sum_{i\in S}\alpha_iy_i\boldsymbol{x}_i^\mathrm{T}\boldsymbol{x}_s\right) b=∣S∣1s∈S∑(ys−i∈S∑αiyixiTxs)
核函数
有时数据并不是线性可分,为解决此问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间线性可分。
令 ϕ ( x ) \phi(\boldsymbol{x}) ϕ(x)表示将 x \boldsymbol{x} x映射后的特征向量: f ( x ) = w T ϕ ( x ) + b f(x)=\boldsymbol{w}^\mathrm{T}\phi(\boldsymbol{x})+b f(x)=wTϕ(x)+b
对偶问题是 max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ϕ ( x i ) T ϕ ( x j ) s . t . ∑ i = 1 m α i y i = 0 , α i ⩾ 0 , i = 1 , 2 , … , m . \max_{\boldsymbol{\alpha}}\sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\phi(\boldsymbol{x}_i)^\mathrm{T}\phi(\boldsymbol{x}_j)\\ \begin{aligned}\mathrm{s.t.}\quad&\sum_{i=1}^m\alpha_iy_i=0, \\ &\alpha_i\geqslant0,\quad i=1,2,\ldots,m. \end{aligned} αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕ(xi)Tϕ(xj)s.t.i=1∑mαiyi=0,αi⩾0,i=1,2,…,m.
为了简化 ϕ ( x i ) T ϕ ( x j ) \phi(\boldsymbol{x}_i)^\mathrm{T}\phi(\boldsymbol{x}_j) ϕ(xi)Tϕ(xj),设想一个函数: κ ( x i , x j ) = ⟨ ϕ ( x i ) , ϕ ( x j ) ⟩ = ϕ ( x i ) T ϕ ( x j ) \kappa(\boldsymbol{x}_i,\boldsymbol{x}_j)=\langle\phi(\boldsymbol{x}_i),\phi(\boldsymbol{x}_j)\rangle=\phi(\boldsymbol{x}_i)^\mathrm{T}\phi(\boldsymbol{x}_j) κ(xi,xj)=⟨ϕ(xi),ϕ(xj)⟩=ϕ(xi)Tϕ(xj)
对偶问题重写为: max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j κ ( x i , x j ) s . t . ∑ i = 1 m α i y i = 0 , α i ⩾ 0 , i = 1 , 2 , … , m . \max_{\boldsymbol{\alpha}}\sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j)\\ \begin{aligned}\mathrm{s.t.}\quad&\sum_{i=1}^m\alpha_iy_i=0, \\ &\alpha_i\geqslant0,\quad i=1,2,\ldots,m. \end{aligned} αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjκ(xi,xj)s.t.i=1∑mαiyi=0,αi⩾0,i=1,2,…,m.
模型为: f ( x ) = w T ϕ ( x ) + b = ∑ i = 1 m α i y i ϕ ( x i ) T ϕ ( x ) + b = ∑ i = 1 m α i y i κ ( x , x i ) + b . \begin{aligned} f(\boldsymbol{x})& =\boldsymbol{w^\mathrm{T}}\phi(\boldsymbol{x})+b \\ &=\sum_{i=1}^m\alpha_iy_i\phi(\boldsymbol{x}_i)^\mathrm{T}\phi(\boldsymbol{x})+b \\ &=\sum_{i=1}^m\alpha_iy_i\kappa(\boldsymbol{x},\boldsymbol{x}_i)+b\mathrm{~.} \end{aligned} f(x)=wTϕ(x)+b=i=1∑mαiyiϕ(xi)Tϕ(x)+b=i=1∑mαiyiκ(x,xi)+b .
κ ( ∗ , ∗ ) \kappa(*,*) κ(∗,∗) 就是核函数。常用核函数如下。

实验
导入数据
from numpy import *
from time import sleep
import random
def loadDataSet(fileName):dataMat = []; labelMat = []fr = open(fileName)for line in fr.readlines():lineArr = line.strip().split('\t')dataMat.append([float(lineArr[0]), float(lineArr[1])])labelMat.append(float(lineArr[2]))return dataMat,labelMat
def selectJrand(i,m):j=i #we want to select any J not equal to iwhile (j==i):j = int(random.uniform(0,m))return jdef clipAlpha(aj,H,L):if aj > H: aj = Hif L > aj:aj = Lreturn aj
dataMat,classLabels=loadDataSet('06testSet.txt')进行数据可视化。
import matplotlib.pyplot as plt
import numpy as np
x = [row[0] for row in dataMat]
y = [row[1] for row in dataMat]
plt.scatter(x, y, c=['blue' if row == 1 else 'red' for row in classLabels])
plt.xlabel('X')
plt.ylabel('Y')plt.show()
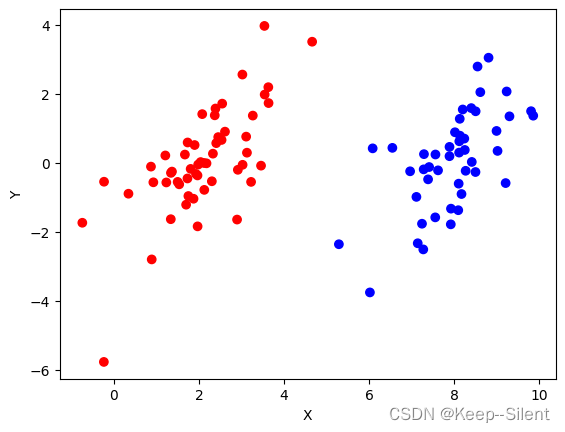
上图可以看出,数据是合法的:可以有一条直线(这条直线就是所需求的超平面)进行划分
实现SMO函数:
创建⼀个alpha向量并将其初始化为0向量
当迭代次数⼩于最⼤迭代次数时(外循环):对数据集中的每个数据向量(内循环):如果该数据向量可以被优化:随机选择另外⼀个数据向量同时优化这两个向量如果两个向量都不能被优化,退出内循环如果所有向量都没被优化,增加迭代数⽬,继续下⼀次循环
Cell In[10], line 1创建⼀个alpha向量并将其初始化为0向量^
SyntaxError: invalid character in identifier
def smoSimple(dataMatIn, classLabels, C, toler, maxIter=50):dataMatrix = mat(dataMatIn)labelMat = mat(classLabels).transpose()b = 0m, n = shape(dataMatrix)alphas = mat(zeros((m, 1)))iter = 0while (iter < maxIter):alphaPairsChanged = 0for i in range(m):fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + bEi = fXi - float(labelMat[i]) # if checks if an example violates KKT conditionsif ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):j = selectJrand(i, m)fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + bEj = fXj - float(labelMat[j])alphaIold = alphas[i].copy()alphaJold = alphas[j].copy()if (labelMat[i] != labelMat[j]):L = max(0, alphas[j] - alphas[i])H = min(C, C + alphas[j] - alphas[i])else:L = max(0, alphas[j] + alphas[i] - C)H = min(C, alphas[j] + alphas[i])if L == H:# print("L==H")continueeta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - dataMatrix[j,:] * dataMatrix[j,:].Tif eta >= 0:# print("eta>=0")continuealphas[j] -= labelMat[j] * (Ei - Ej) / etaalphas[j] = clipAlpha(alphas[j], H, L)if (abs(alphas[j] - alphaJold) < 0.00001):# print("j not moving enough")continuealphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[i, :] * dataMatrix[j, :].Tb2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].Tif (0 < alphas[i]) and (C > alphas[i]):b = b1elif (0 < alphas[j]) and (C > alphas[j]):b = b2else:b = (b1 + b2) / 2.0alphaPairsChanged += 1print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))if (alphaPairsChanged == 0):iter += 1else:iter = 0print("iteration number: %d" % iter)return b, alphasb, alphas = smoSimple(dataMat, classLabels, 0.6, 0.001, maxIter=50)
b=b[0,0]
部分运行结果:
iter: 0 i:1, pairs changed 1
iter: 0 i:3, pairs changed 2
iter: 0 i:4, pairs changed 3
iter: 0 i:8, pairs changed 4
iter: 0 i:10, pairs changed 5
iter: 0 i:14, pairs changed 6
iter: 0 i:29, pairs changed 7
iter: 0 i:55, pairs changed 8
iteration number: 0
iter: 0 i:1, pairs changed 1
iter: 0 i:24, pairs changed 2
iter: 0 i:27, pairs changed 3
iter: 0 i:29, pairs changed 4
iter: 0 i:55, pairs changed 5
iter: 0 i:76, pairs changed 6
iteration number: 0
iter: 0 i:8, pairs changed 1
iter: 0 i:55, pairs changed 2
iter: 0 i:84, pairs changed 3
iteration number: 0
iter: 0 i:4, pairs changed 1
iter: 0 i:11, pairs changed 2
iter: 0 i:46, pairs changed 3
iter: 0 i:52, pairs changed 4
iter: 0 i:54, pairs changed 5
iteration number: 0
iter: 0 i:1, pairs changed 1
iter: 0 i:22, pairs changed 2
iter: 0 i:24, pairs changed 3
iter: 0 i:30, pairs changed 4
iteration number: 0
iter: 0 i:10, pairs changed 1
iteration number: 0
iter: 0 i:18, pairs changed 1
...
iteration number: 38
iteration number: 39
iteration number: 40
iteration number: 41
iteration number: 42
iteration number: 43
iteration number: 44
iteration number: 45
iteration number: 46
iteration number: 47
iteration number: 48
iteration number: 49
iteration number: 50
输出b和alphas
print(b)
print(alphas)
部分运行结果:
-3.7617698556024015
[[0. ]...[0. ][0.12836263][0. ][0. ][0. ]...[0. ][0.23620881][0. ]...[0. ]]
计算超平面向量 w = ∑ i = 1 m α i y i x i \boldsymbol{w}=\sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i w=∑i=1mαiyixi
def GetW(alphas,classLabels,dataMat):w=np.zeros(2)sv=[]for i in range(len(dataMat)):if alphas[i,0]>0:sv.append(i)w+= alphas[i,0]*classLabels[i]*np.array(dataMat[i])return sv,w
sv,w= GetW(alphas,classLabels,dataMat)
print(sv)
print(w)
[17, 29, 55]
[ 0.80226906 -0.27808456]
由 w 0 x + w 1 y + b = 0 w_0x+w_1y+b=0 w0x+w1y+b=0 可得 y = − w 0 x − b w 1 y=\cfrac{-w_0x-b}{w_1} y=w1−w0x−b
x = [row[0] for row in dataMat]
y = [row[1] for row in dataMat]
color=['blue' if classLabel == 1 else 'red' for classLabel in classLabels]
for i in sv:color[i]='black'
plt.scatter(x, y, c=color)
plt.xlabel('X')
plt.ylabel('Y')x = np.linspace(min(x), max(x), 100)
y =(-w[0]*x-b)/w[1]plt.plot(x, y)plt.show()
如上图所示,将支持向量标记为黑点,其余平面两边的点分别标记为红点和蓝点。
通过该支持向量机算法,我们可以求得支持向量、求得超平面方程,将数据进行划分。⽀持向量机的泛化错误率较低,也就是说它具有良好的学习能⼒,且学到的结果具有很好的推⼴性。
相关文章:

第六章 支持向量机
文章目录 支持向量机间隔和支持向量对偶问题问题推导SMO 核函数实验 支持向量机 ⽀持向量机(Support Vector Machines,SVM) 优点:泛化错误率低,计算开销不⼤,结果易解释。缺点:对参数调节和核…...

Docker基本操作之删除容器Container和删除镜像IMAGE
一、删除容器Container语法 docker rm [OPTIONS] CONTAINER [CONTAINER...]OPTIONS参数说明: -f :通过 SIGKILL 信号强制删除一个运行中的容器。【注意是正在运行的容器实例】-l :移除容器间的网络连接,而非容器本身。-v :删除与容器关联的卷。即删除容…...
vue 3.0 + element-ui MessageBox弹出框的 让文本框显示文字 placeholder
inputPlaceholder:请填写理由, 方法实现如下: this.$prompt(, 是否确认?, { confirmButtonText: 确定, cancelButtonText: 取消, inputPlaceholder:请填写理由, }).then(({ value }) > { if(value null || value ""){ Message({message: 请填…...
QT生成可执行文件的步骤
QT生成可执行文件的步骤 第一步:debug为release,然后进行编译 第二步:添加QT生成必要的库 首先,建立一个新的文件夹,然后将Release中的可执行文件拷贝到新的文件夹中 然后,在新建文件夹中生成必要的库 …...
一分钟学会JS获取当前年近五年的年份
先看效果图 上代码: 1、HTML <div><el-date-pickerv-model"queryYearXmgk.startYear"format"yyyy"value-format"yyyy"type"year"placeholder"开始"clearable:picker-options"pickerStartAuditYe…...

14 springboot项目——首页跳转实现
templates里的静态资源无法访问,需要写mvc的配置类或者改application.xml配置文件实现首页访问。这两个方式用其中一种即可,否则会冲突。 14.1 首页跳转方式一 创建配置类,在config包中创建一个mvc的配置类: package jiang.com.s…...
IL汇编语言读取控制台输入和转换为整数
新建一个testcvt.il; .assembly extern mscorlib {}.assembly Test{.ver 1:0:1:0}.module test.exe.method static void main() cil managed{.maxstack 1.entrypointldstr "\n请输入一个数字:"call void [mscorlib]System.Console::Write(string)call st…...
什么是跨链 DeFi?
跨链 DeFi 是指存在于多个不同区块链生态系统之间的金融应用程序生态系统,可以在彼此之间无缝交换数据和通证。 Web3 生态系统已经变得多链化,存在于数百个区块链、二层网络、应用链和其他环境的去中心化应用繁荣发展。虽然多样化的区块链生态系统的推出…...

Linux下C/C++的gdb工具与Python的pdb工具常见用法之对比
1、gdb和pdb分别是什么? 1.1、gdb GDB(GNU Debugger)是一个功能强大的命令行调试工具,由GNU项目开发,用于调试C、C等编程语言的程序。它在多个操作系统中都可以使用,包括Linux、MacOS和Windows࿰…...
从入门到专业:探索Python中的判断与循环技巧!
文章目录 判断语句布尔类型和比较运算符if语句的基本格式练习案例:成年人判断if else语句if elif else语句判断语句的嵌套案例:猜数字 循环语句while循环的基础语法while循环的基础案例while循环的嵌套应用补充:print输出不换行&\tfor循环…...

mqtt、tcp、http的区别
文章目录 一、MQTT(Message Queuing Telemetry Transport)1、类型2、用途 二、TCP(Transmission Control Protocol)1、类型2、用途 三、HTTP(Hypertext Transfer Protocol)1、类型2、用途 四、主要区别1、类…...

边写代码边学习之RNN
1. 什么是 RNN 循环神经网络(Recurrent Neural Network,RNN)是一种以序列数据为输入来进行建模的深度学习模型,它是 NLP 中最常用的模型。其结构如下图: x是输入,h是隐层单元,o为输出ÿ…...
在linux调试进程PID的方法
当我们谈论调试 PID(进程标识符)时,我们通常是指诊断和解决与操作系统中的特定进程相关的问题。有许多工具和方法可用于调试 PID,以下是一些常见的方法: 1. 使用ps命令 ps命令是最基本的调试工具,用于查看…...

【并发编程】线程安全的栈容器
std::stack容器的接口包括 empty(), size(), top(), push(), pop()等。 问题 其原接口在多线程的情况下,会持续很多问题。 例如,在std::stack容器的接口中,在多线程下应用时,empty()和size()的结果是不可信的。因为尽管在某线程…...

ES嵌套查询和普通查询的高亮显示区别
在 Elasticsearch 中,高亮显示是一种强大的搜索结果可视化工具,它可以帮助我们快速识别匹配的关键字或短语。在ES中,我们可以使用两种不同的查询方式来实现高亮显示:嵌套查询和普通查询。本文探讨这两种查询方式的高亮显示区别以及…...

Greenplum集群部署
一,安装说明 1.1环境说明 *名称**版本*操作系统CentOS 7.6 64bitgreenplumgreenplum-db-6.10.1-rhel7-x86_64.rpm1.2集群介绍 IPhostname集群节点10.240.3.244gpmastermaster10.240.3.245gpsegment1segment10.240.3.246gpsegment2segment二,安装环境准备 2.1 修改各节点名称…...

电教智能云数据可视化平台开发电能优化日志实录
电教智能云数据可视化平台开发电脑优化日志实录 一、2K和4K弹窗判断二、电能API对接1.电脑爬虫2.电能分组过滤3.数据可视化渲染4.弹窗 三.数组按顺序输出 一、2K和4K弹窗判断 {* 判断2k和4k弹窗 *}{if $dataScene[scene_standard] eq 0}<a class"menuBtn subMenu"…...

JSX语法基础总结
题记:首先我们要了解一下jsx是什么,跟js有什么区别,其实就是js的语法糖,加上了xml的语法,使得产生虚拟dom更加的方便,简单说一下,xml就是存储数据的格式,想了解xml的话,可…...
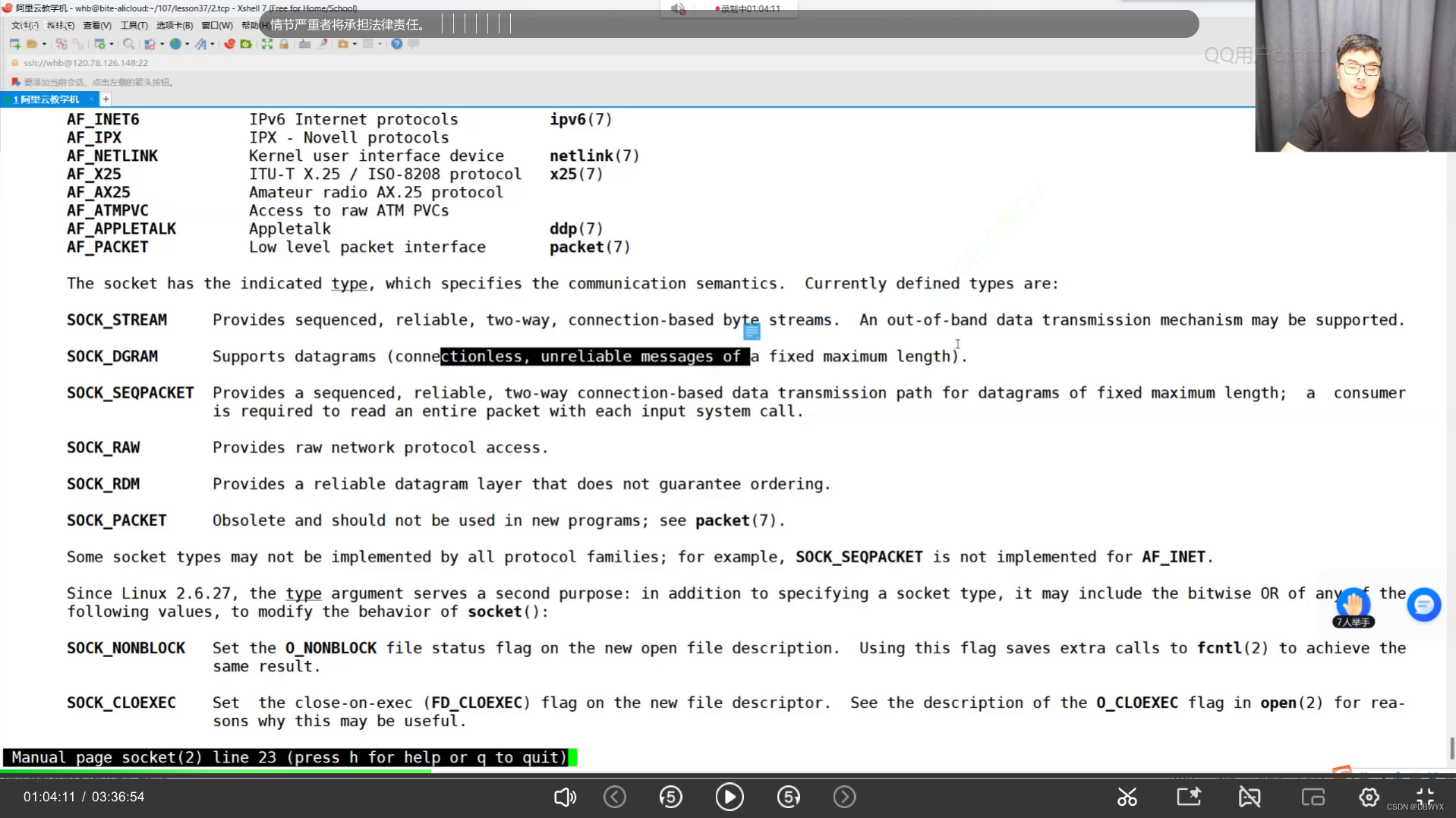
socker套接字
1.打印错误信息 2.socketaddr_in结构体 结构体: (部分库代码) (宏中的##) 3.manual TCP: SOCK_STREAM : 提供有序地,可靠的,全双工的,基于连接的流式服务 UDP: 面向数据报...
No111.精选前端面试题,享受每天的挑战和学习
文章目录 map和foreach的区别在组件中如何获取vuex的action对象中的属性怎么去获取封装在vuex的某个接口数据有没有抓包过?你如何跟踪某一个特定的请求?比如一个特定的URL,你如何把有关这部分的url数据提取出来?1. 使用网络抓包工…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...
