【第37天】斐波那契数列与爬楼梯 | 迭代的鼻祖,递推与记忆化
学习指引
- 序、专栏前言
- 一、递推与记忆化
- 二、【例题1】
- 1、题目描述
- 2、解题思路
- 3、模板代码
- 4、代码解析
- 5.原题链接
- 三、【例题1】
- 1、题目描述
- 2.解题思路
- 3、模板代码
- 4、代码解析
- 5、原题链接
- 三、推荐专栏
- 四、课后习题
序、专栏前言
本专栏开启,目的在于帮助大家更好的掌握学习Java,特别是一些Java学习者难以在网上找到系统地算法学习资料帮助自身入门算法,同时对于专栏内的内容有任何疑问都可在文章末尾添加我的微信给你进行一对一的讲解。
但最最主要的还是需要独立思考,对于本专栏的所有内容,能够进行完全掌握,自己完完全全将代码写过一遍,对于算法入门肯定是没有问题的。
算法的学习肯定不能缺少总结,这里我推荐大家可以到高校算法社区将学过的知识进行打卡,以此来进行巩固以及复习。
学好算法的唯一途径那一定是题海战略,大量练习的堆积才能练就一身本领。专栏的任何题目我将会从【题目描述】【解题思路】【模板代码】【代码解析】等四板块进行讲解。
一、递推与记忆化
在算法的学习中,有许多的题目需要我们递推得到答案,这需要我们去发掘出递推式子得到答案。就好比我们在一个有向图上想要到达终点,需要从起点一步步找到终点,所以相邻的点之间一定会有着某种关联,这种关联就是我们的递推式。斐波那契数列和爬楼梯两道题可以说是所有递推入门的经典题目,同时递推思想也可以看作是最简单动态规划思想。当然在递推时,为了减少重复计算,我们还用叫做记忆化的优化方法,可以帮我们节省大量的时间。
二、【例题1】
1、题目描述
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1F(N) = F(N - 1) + F(N - 2), 其中 N > 1.- 斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
2、解题思路
核心在于递推式:F(N)=F(N−1)+F(N−2)F(N) = F(N - 1) + F(N - 2)F(N)=F(N−1)+F(N−2)
显然式子含义为每个数为前两个数之和,我们根据式子递推即可。
3、模板代码
超时代码:
class Solution {public int fib(int n) {return f(n);}int f(int x){if(x==1) return 1;if(x==0) return 0;return (f(x-1)+f(x-2))%1000000007;}
}
递归记忆化代码:
class Solution {int[] a=new int[110];public int fib(int n) {Arrays.fill(a,-1);a[0]=0;a[1]=1;dfs(n);return a[n];}int dfs(int x){if(a[x]!=-1) return a[x];return a[x]=(dfs(x-1)+dfs(x-2))%1000000007;}
}
递推代码:
class Solution {public int fib(int n) {if(n==0) return 0;int[] f=new int[n+1];f[0]=0;f[1]=1;for(int i=2;i<=n;++i){f[i]=(f[i-1]+f[i-2])%1000000007;}return f[n];}
}
4、代码解析
显然,无论是递推还是记忆化代码,我们都需要使用数组记录答案,否则当我们求解 f(n)f(n)f(n)时,本来我们已经计算出了f(n−1)f(n-1)f(n−1)和f(n−2)f(n-2)f(n−2),结果又得重新计算一次,从而导致计算量变大超时。可以直接使用数组递推时,其本身就有记忆化功能,如果使用递归来进行 dpdpdp,则大家最好加上记忆化。
5.原题链接
斐波那契数列
三、【例题1】
1、题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
2.解题思路
定义 f(n)f(n)f(n)为走到第 nnn 阶楼梯有多少种走法,显然第 nnn 阶只能从第 n−1n-1n−1 或者 n−2n-2n−2 阶走过来,于是我们得到递推式:
f(n)=f(n−1)+f(n−2)f(n) = f(n - 1) + f(n - 2)f(n)=f(n−1)+f(n−2)
(惊喜发现这不是和斐波那契数列一样的吗哈哈哈,那么题目迎刃而解啦,但是注意初始化有略微区别
3、模板代码
递推代码:
class Solution {public int climbStairs(int n) {int[] f=new int[n+1];if(n==1) return 1;f[1]=1;f[2]=2;for(int i=3;i<=n;++i){f[i]=f[i-1]+f[i-2];}return f[n];}
}
递推记忆化代码:
class Solution {int[] f=new int[50];public int climbStairs(int n) {Arrays.fill(f,-1);if(n==1) return 1;f[1]=1;f[2]=2;dfs(n);return f[n];}int dfs(int x){if(f[x]!=-1) return f[x];return f[x]=dfs(x-1)+dfs(x-2);}
}
4、代码解析
注意到爬楼梯和斐波那契初始化不同,递推式相同。
5、原题链接
爬楼梯

三、推荐专栏
四、课后习题
| 序号 | 题目链接 | 难度评级 |
|---|---|---|
| 1 | 使用最小花费爬楼梯 | 1 |
相关文章:

【第37天】斐波那契数列与爬楼梯 | 迭代的鼻祖,递推与记忆化
本文已收录于专栏🌸《Java入门一百例》🌸学习指引序、专栏前言一、递推与记忆化二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析5.原题链接三、【例题1】1、题目描述2.解题思路3、模板代码4、代码解析5、原题链接三、推荐专栏四、课后习题序…...
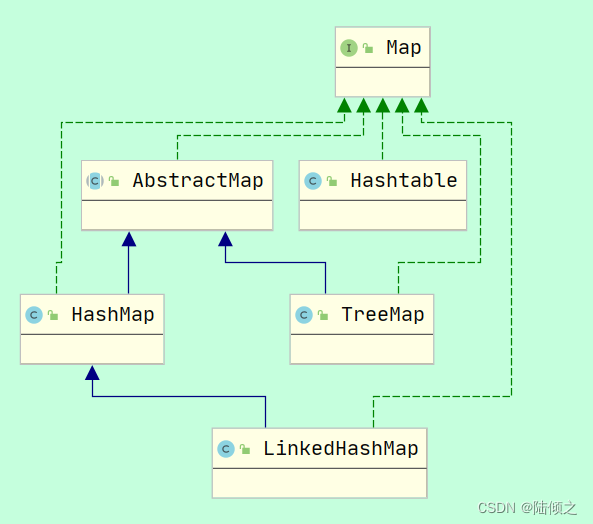
Map集合
Map集合 Map接口的简介 Map用于保存具有映射关系的数据,Map里保存着两组数据:key和value,它们都可以使任何引用类型的数据,但key不能重复。所以通过指定的key就可以取出对应的value。 Map 没有继承 Collection 接口,…...
PyQt5编程扩展 3.2 资源文件的使用
目录 本例运行效果: 设计Qt窗体 建立项目 放一个Group Box 放三个Label 放一个Horizontal Slider 放两个Line Edit 层次结构 布局 放一个Group Box 放两个Label 放两个Line Edit 放一个Push Button 层次结构 布局 放一个frame 层次结构 布局 窗体…...

Linux系统之文件共享目录设置方法
Linux系统之文件共享目录设置方法一、本次实践目的二、检查本地系统环境1.检查系统版本2.检查系统内核三、创建相关用户及用户组1.创建共享目录2.创建测试用户账号3.创建用户组4.设置用户的属组5.查看admin和IT用户组成员6.查看所有用户信息四、共享目录权限设置1.设置/data/so…...
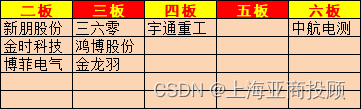
上海亚商投顾:三大指数均涨超1% 芯片板块集体大涨
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。市场情绪三大指数今日低开高走,午后集体涨超1%,创业板指盘中涨超1.7%。芯片板块集体大涨,…...

Harbor私有仓库部署与管理
目录 前言 一、Harbor概述 二、Harbor 的特性 三、Harbor的构成 四、Harbor构建Docker私有仓库 1、环境配置 2、案例需求 3、部署Harbor服务 3.1、部署docker compose服务 3.2 下载或上传Harbor安装程序 3.3、启动Harbor 3.4、查看Harbor启动镜像 4、物理机访问se…...

互联网架构之 “高可用” 详解
一、什么是高可用 高可用HA(High Availability)是分布式系统架构设计中必须考虑的因素之一,它通常是指,通过设计减少系统不能提供服务的时间。 假设系统一直能够提供服务,我们说系统的可用性是100%。 如果系统每运行…...
分布式高级篇4 —— 商城业务(2)
一、订单服务1、订单基本概念2、订单基本构成3、订单状态4、订单流程5、配置拦截器拦截订单请求6、订单确认页模型抽取7、订单确认页vo封装8、Feign 远程调用请求头丢失问题\*\*\*\*\* 惨痛教训9、Feign 异步调用请求头丢失问题10、查看库存状态11、模拟计算运费12、接口幂等性…...

二分查找基本原理
二分查找基本原理1.二分查找1.1 基本概念1.2 二分查找查找步骤1.2.1 中间索引不能整除,取整数作为中间索引1.2.2 索引不能整除,整数1作为中间索引1.3 二分查找大O记法表示2. 二分查找代码实现1.二分查找 1.1 基本概念 二分法(折半查找)是一…...

【Python实战案例】Python3网络爬虫:“可惜你不看火影,也不明白这个视频的分量......”m3u8视频下载,那些事儿~
前言 哈喽!上午好嘞,各位小可爱们!有没有等着急了呀~ 由于最近一直在学习新的内容,所以耽搁了一下下,抱歉.jpg 双手合十。 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移…...

UE4:使用样条生成随机路径,并使物体沿着路径行走
一、关于样条的相关知识 参考自:样条函数 - 馒头and花卷 - 博客园 三次样条(cubic spline)插值 - 知乎 B-Spline(三)样条曲线的性质 - Fun With GeometryFun With Geometry 个人理解的也不是非常深,但是大概要知道的就是样条具…...
)
计算机组成原理(判断题)
计算机控制器是根据事先编好的程序,根据其指令来进行控制只会每一步骤的操作; 面向主存的双总线结构计算机系统,因在CPU与主存之间增加了一组存储器总线,由于通过存储器总线访存,提高了CPU的访存速度,也减轻…...

error: failed to push some refs to ... 就这篇,一定帮你解决
目录 一、问题产生原因 二、解决办法 三、如果还是出问题,怎么办?(必杀) 一、问题产生原因 当你直接在github上在线修改了代码,或者是直接向某个库中添加文件,但是没有对本地库同步,接着你想…...
DAMA数据管理知识体系指南之数据仓库和商务智能管理
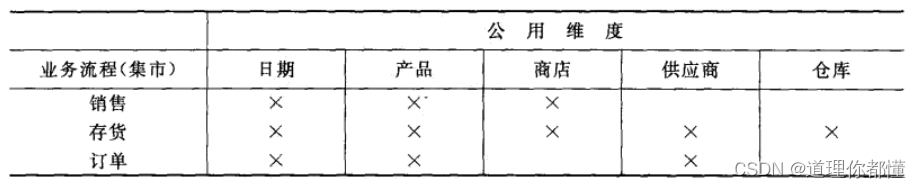
第9章 数据仓库和商务智能管理 9.1简介 数据仓库(Data Warehouse,DW)由两个主要部分构成:首先是一个整合的决策支持数据库,其次是用于收集、清洗、转换、存储来自于各种操作型数据源和外部数据源数据的相关软件程序。两者结合以支持历史的、…...

PHP的五种常见设计模式
工厂模式 最初在设计模式 一书中,许多设计模式都鼓励使用松散耦合。要理解这个概念,让我们最好谈一下许多开发人员从事大型系统的艰苦历程。在更改一个代码片段时,就会发生问题,系统其他部分 —— 您曾认为完全不相关的部分中也有…...

教你搞懂线段树,从基础到提高
秋名山码民的主页 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 🙏作者水平有限,如发现错误,还请私信或者评论区留言! 目录前言线段树逻辑概念线段树的俩个重要用处代码实现线段树题目巩固最后…...

C语言进阶——自定义类型:结构体
🌇个人主页:_麦麦_ 📚今日名言:生活不可能像你想象的那么好,也不会像你想象的那么糟。——莫泊桑《羊脂球》 目录 一、前言 二、正文 1结构体 1.1结构体的基础知识 1.2结构的声明 1.3特殊的声明 1.4结构体变量的…...

SpringSecurity学习笔记01
目录 一、课程介绍 二、框架概述 三、入门案例 四、基本原理(过滤器链) 五、基本原理(过滤器加载过程) 六、基本原理(两个重要的接口) 七、web权限方案-用户认证(设置用户名密码上) 八、…...
Python语言零基础入门教程(十一)
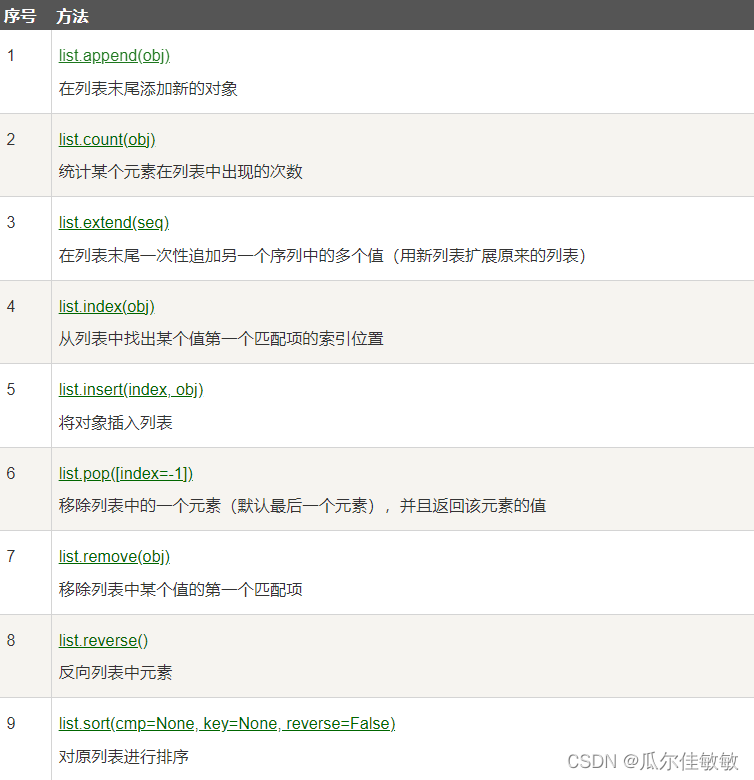
Python 列表(List) 序列是Python中最基本的数据结构。序列中的每个元素都分配一个数字 - 它的位置,或索引,第一个索引是0,第二个索引是1,依此类推。 Python有6个序列的内置类型,但最常见的是列表和元组。 序列都可以…...

现货白银基础知识
任何活动,任何项目,任何工作都离不开基础知识,这是肯定的。万丈高楼平地起,要想要简称百层高楼,首先得把低级打好!现货白银投资也是一样的道理,现在我们就来一起聊聊现货白银基础知识的问题&…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
