【每日一题Day122】LC1237找出给定方程的正整数解 | 双指针 二分查找
找出给定方程的正整数解【LC1237】
给你一个函数
f(x, y)和一个目标结果z,函数公式未知,请你计算方程f(x,y) == z所有可能的正整数 数对x和y。满足条件的结果数对可以按任意顺序返回。尽管函数的具体式子未知,但它是单调递增函数,也就是说:
f(x, y) < f(x + 1, y)f(x, y) < f(x, y + 1)函数接口定义如下:
interface CustomFunction { public:// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.int f(int x, int y); };你的解决方案将按如下规则进行评判:
- 判题程序有一个由
CustomFunction的9种实现组成的列表,以及一种为特定的z生成所有有效数对的答案的方法。- 判题程序接受两个输入:
function_id(决定使用哪种实现测试你的代码)以及目标结果z。- 判题程序将会调用你实现的
findSolution并将你的结果与答案进行比较。- 如果你的结果与答案相符,那么解决方案将被视作正确答案,即
Accepted。
说真的 我看了评论区才看懂题目的
暴力
-
思路:双重循环枚举每个可能的xxx和yyy,通过
customfunction.f(x, y)求出运算结果,如果结果等于zzz,那么加入结果集中;由于函数是单调递增函数,因此如果结果大于zzz时,退出循环。 -
实现
class Solution {public List<List<Integer>> findSolution(CustomFunction customfunction, int z) {List<List<Integer>> res = new ArrayList<>();for (int i = 1; i <= 1000; i++){for (int j = 1; j <= 1000; j++){int num = customfunction.f(i, j);if (num == z){res.add(Arrays.asList(i, j));}else if (num > z){break;}}}return res;} }-
复杂度
- 时间复杂度:O(C2)O(C^2)O(C2),CCC为x和y的取值范围,本题中为100010001000
- 空间复杂度:O(1)O(1)O(1)
-
二分查找
-
思路:由于函数为单调递增函数,因此可以固定xxx,二分查找yyy,二分查找的上限为1,下限为1000,假定运算结果为numnumnum
- 如果num==znum==znum==z,那么将结果添加至结果集
- 如果num>znum>znum>z,那么yyy向左边查询,right = mid - 1
- 如果num==znum==znum==z,那么yyy向右边查询,left = mid + 1
-
实现
/** // This is the custom function interface.* // You should not implement it, or speculate about its implementation* class CustomFunction {* // Returns f(x, y) for any given positive integers x and y.* // Note that f(x, y) is increasing with respect to both x and y.* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)* public int f(int x, int y);* };*/class Solution {public List<List<Integer>> findSolution(CustomFunction customfunction, int z) {List<List<Integer>> res = new ArrayList<>();for (int i = 1; i <= 1000; i++){int jL = 1, jR = 1000;while (jL <= jR){int mid = (jL + jR) / 2;int num = customfunction.f(i, mid);if (num == z){res.add(Arrays.asList(i, mid));break;}else if (num > z){jR = mid - 1;}else{jL = mid + 1;}}}return res;} }-
复杂度
- 时间复杂度:O(ClogC)O(ClogC)O(ClogC),CCC为x和y的取值范围,本题中为100010001000
- 空间复杂度:$O(1) $
-
双指针
-
思路:当x1<x2x_1<x_2x1<x2时,如果f(x1,y1)=f(x2,y2)=zf(x_1,y_1)=f(x_2,y_2)=zf(x1,y1)=f(x2,y2)=z,那么此时y1>y2y_1>y_2y1>y2,因此可以从小到大枚举xxx,从大到小枚举yyy,那么可以固定xxx,在上次循环的yyy值作为起始值,找到本次的yyy。
-
实现
class Solution {public List<List<Integer>> findSolution(CustomFunction customfunction, int z) {List<List<Integer>> res = new ArrayList<>();int j = 1000;for (int i = 1; i <= 1000; i++){while (j >= 1 && customfunction.f(i, j) > z){j--;}if (j >= 1 && customfunction.f(i, j) == z){res.add(Arrays.asList(i, j));}}return res;} }-
复杂度
- 时间复杂度:O(C)O(C)O(C),CCC为x和y的取值范围,本题中为100010001000
- 空间复杂度:$O(1) $
-
相关文章:

【每日一题Day122】LC1237找出给定方程的正整数解 | 双指针 二分查找
找出给定方程的正整数解【LC1237】 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知,但它是单调递增函数&#…...
笔记本加装固态和内存条教程(超详细)
由于笔记本是几年前买的了,当时是4000,现在用起来感到卡顿,启动、运行速度特别慢,就决定换个固态硬盘,加个内存条,再给笔记本续命几年。先说一下加固态硬盘SSD的好处:1.启动快 2.读取延迟小 3.写…...

【Python】字典 - Dictionary
字典 - Dictionarykeys()values()items()get()获取文件中指定字符的个数进阶版:获取所有单词的频数进阶版:获取所有字符的频数函数内容keys()输出字典中的所有键values()输出字典中的所有值items()以元组的形式输出键值对get()获取字典中指定键的值 keys…...
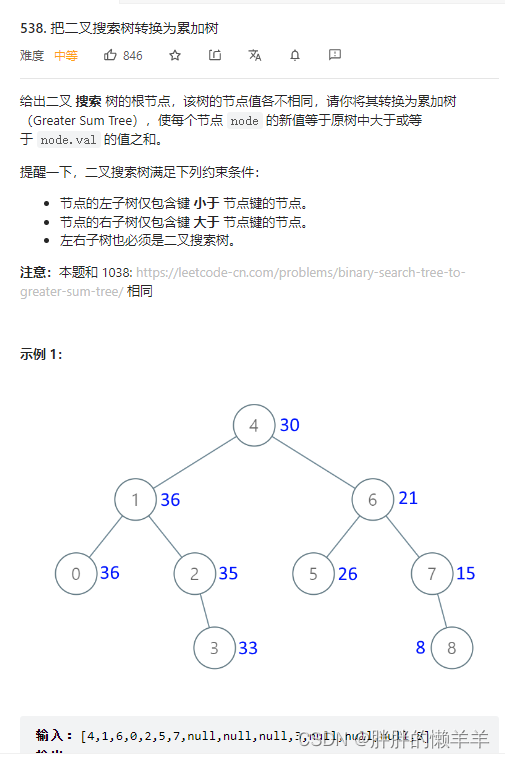
LeetCode分类刷题----二叉树
二叉树1.二叉树的递归遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历2.二叉树的迭代遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历3.二叉树的层序遍历102.二叉树的层序遍历107.二叉树的层序遍历||199.二叉树的右视图637.二叉树的层平均…...
)
Zipkin : Golang 微服务全链路监控(三)
Zipkin : Golang 微服务全链路监控(三) Golang 微服务全链路监控实现 broker-service -> auth-service -> postgres dbzipkin 监控:需代码入侵 使用 zipkin 库的 serverMiddleware,其通过 Http 跟踪(trace&am…...
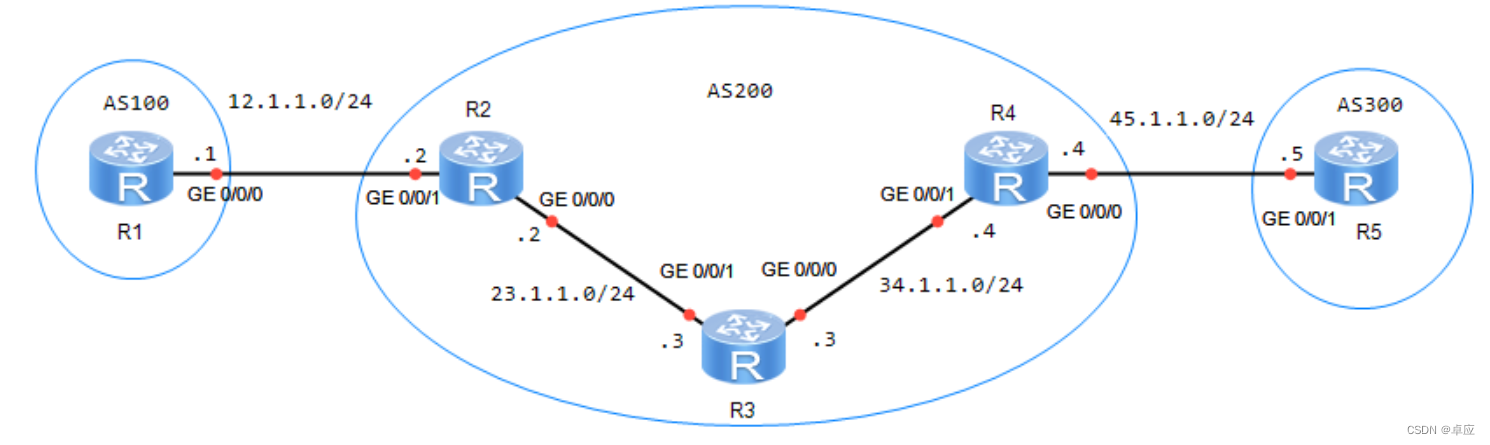
5.3 BGP路由黑洞
5.2.3实验3:BGP路由黑洞 1. 实验目的 熟悉BGP路由黑洞的应用场景掌握BGP水平分割的配置方法2. 实验拓扑 实验拓扑如图5-3所示: 图5-3:BGP路由黑洞 3. 实验步骤 配置IP地址 R1的配置 <Huawei>syst...
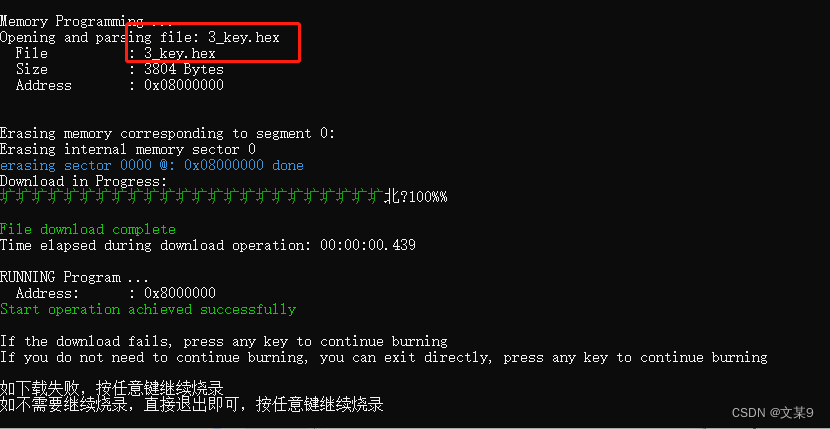
STM32 DFU模式烧录代码
什么是DFU? dfu的本质是isp,usb接口的isp,在系统编程,进入isp的方式我们先了解 如下图 boot0为高电平 boot1为低电平即可进入isp模式。 熟悉的场景 在我们使用flymcu软件下载代码时,本质也是isp 串口接口的isp。 傻瓜使用方式…...
松下PLC通过fpwin上传写入MRTC模块方法
目录 PLC程序上传方法 加密模块使用 PLC程序上传方法 手动将PLC模式设置为prog模式查看PLC是否设置为禁止上传查询指示灯是否变蓝,变蓝则需要将PLC禁止上传功能取消。 3.当上述动作操作完成后,将PLC程序导入到PLC中。为了配合加密程序使用,…...

就业大山之下的网络安全:安逸的安服仔
从去年开始,各个互联网大厂就接二连三的放出了裁员消息,整个互联网行业好像都处于寒冬状态。微博、小米、滴滴、知乎、拼多多等在内的一大批互联网知名企业,也相继传出“人员优化”的消息。 除了国内市场的萧条,国外市场也是不容…...
JavaWeb3-线程的3种创建方式7种写法
目录 1.方式一:继承Thread(2种写法) 写法①(常规): a.使用jconsole观察线程 b.启动线程——start方法 PS:(常见面试题)start 方法与 run 方法的区别: 写…...

驱动调试手段
文章目录 前言一、通过sysfs调试LCD查看电源:查看 pwm 信息查看管脚信息总结前言 本文记录在驱动中常用的调试手段 提示:以下是本篇文章正文内容,下面案例可供参考 一、通过sysfs 系统起来之后可以读取 sysfs 一些信息,来协助调试 示例: 调试LCD 输入如下命令 cat /…...

[RK3568 Android12] 音频及路由
1:概述(耳机 ,hdmiin ,板载喇叭) 在开发板上面,系统注册了三个音频输出通道,如下: [ 2.280612] ALSA device list: [ 2.280622] #0: rockchip,rk809-codec [ 2.280630] #1: ROCKCHIP,SPDIF [ 2.280638] #2: rockchip,hdmi console:/proc/asound # cat pcm …...

C++——C++11 第一篇
目录 统一的列表初始化 {}初始化 decltype 编辑 nullptr STL中一些变化 右值引用和移动语义 左值引用和右值引用 总结 左值引用优缺点 右值引用(将亡值) 拷贝赋值和移动赋值 万能引用|完美转发 移动构造和移动赋值注意…...
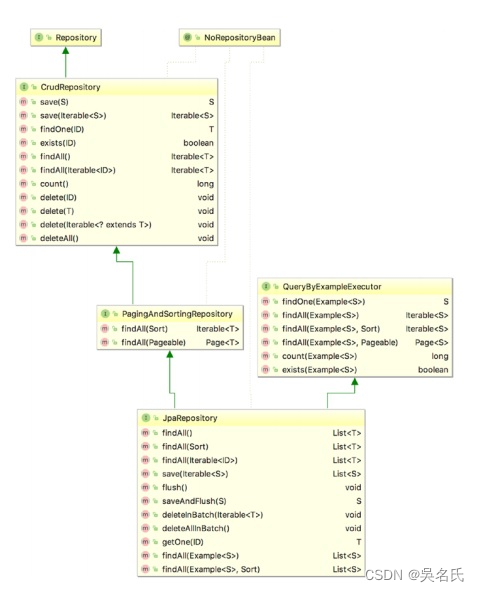
Spring Data JPA 中 CrudRepository 和 JpaRepository 的区别
1 问题描述Spring Data JPA 中,CrudRepository 和 JpaRepository 有何区别?当我在网上找例子的时候,发现它们可以互相替换使用。它们有什么不同呢?为什么你习惯用其中的一个而不是另一个呢?2 CrudRepository 和 JpaRep…...

推荐几款好用的数据库管理工具
本文主要介绍几款常用的数据库管理软件(客户端),包括开源/免费的、商用收费的,其中有一些是专用于 MySQL 数据库的,例如 MySQL Workbench、phpMyAdmin,有一些是支持多种 SQL、NoSQL 数据库的,例…...

DPDK — 性能优化手段
目录 文章目录 目录硬件布局层面的优化操作系统层面的优化Linux 操作系统版本应用程序层面的优化Cache 优化内存对齐内存预取SIMD 报文批处理DDIO使用高级 CPU 指令集硬件布局层面的优化 DPDK 在硬件布局层面的优化,主要体现在以下几个方面: CPU 频率的高低:CPU 频率越高,…...

Fedora Linux未来五年规划
Fedora 委员会一直致力于起草战略计划,以帮助 Fedora Linux 更好地发展。近日 Fedora 委员会公布了一份 “《未来五年的 Fedora Linux 》” 战略计划草案,这份草案里面包含了他们的雄心壮志:每周将 Fedora 的活跃贡献者人数增加一倍。 Fedora…...
【C++之容器篇】map和set常见函数接口的使用与剖析
目录前言一、set1. 简介2. 成员类型3. 构造函数(1) set()(2)set(InputIterator first,InputIterator last)(3)使用4. 拷贝构造函数和赋值运算符重载5. empty()6. size()7. insert()(1)pair<iterator,bool> insert(const K& key)(2)iterator insert(iterator pos,cons…...
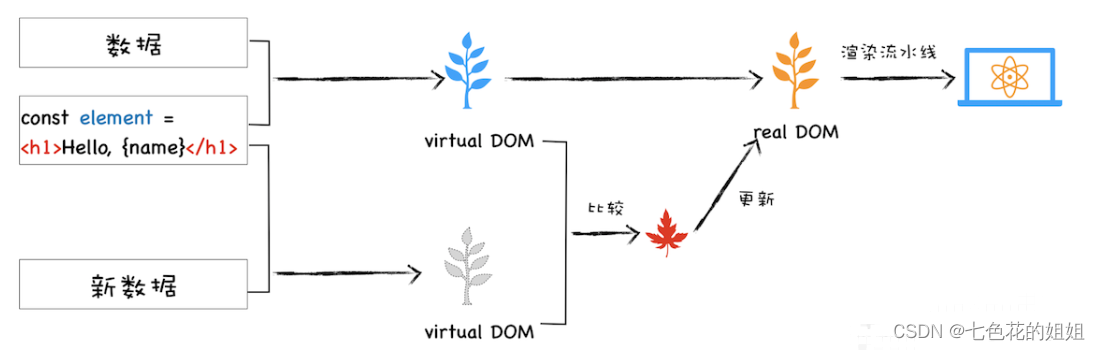
虚拟DOM是什么
参考文章做的总结,如有不足之处请指正! 在讲虚拟dom之前,先讲讲,为什么前端操作dom会导致页面性能降低? 先说几个概念 有助于后面的理解 什么是 JavaScript 引擎? JavaScript引擎是一个专门处理JavaScript脚…...
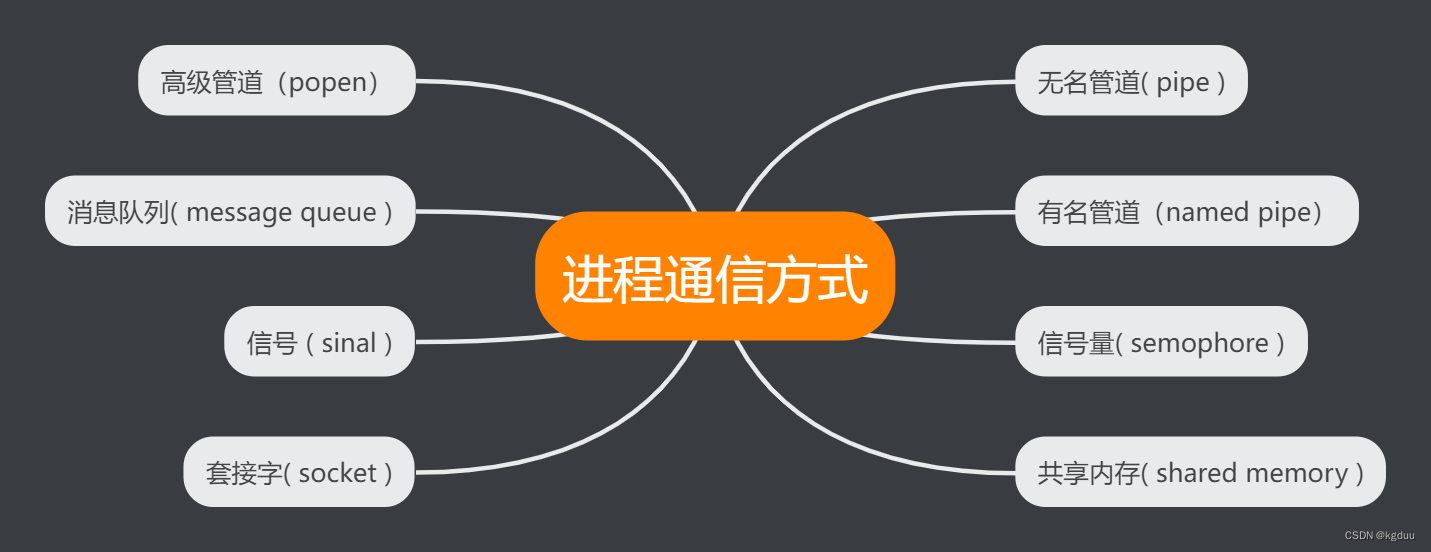
进程通信方式
无名管道( pipe ): 管道是一种半双工的通信方式,数据只能单向流动,而且只能在具有亲缘关系的进程间使用。进程的亲缘关系通常是指父子进程关系。高级管道(popen): 将另一个程序当做一个新的进程在当前程序进…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
