LeetCode-1237. 找出给定方程的正整数解【双指针,二分查找】
LeetCode-1237. 找出给定方程的正整数解【双指针,二分查找】
- 题目描述:
- 解题思路一:双指针。首先我们不管f是什么,即function_id等于什么不管。但是我们可以调用customfunction中的f函数,然后我们遍历x,y(1 <= x, y <= 1000)只要f(x,y)=z的(x,y)即是我们需要的答案。然后我们从x=1与y=1000开始遍历。此时有三种情况:
- 解题思路二:二分查找。枚举x,二分查找y。找到之后x增大因为f对x,y递增故之后的y必小于middle。即f(x,middle)=z若要f(x+1,y)=z那么y必小于middle;对右边界的优化。
- 解题思路三:0
题目描述:
给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。
尽管函数的具体式子未知,但它是单调递增函数,也就是说:
f(x, y) < f(x + 1, y)
f(x, y) < f(x, y + 1)
函数接口定义如下:
interface CustomFunction {
public:
// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.
int f(int x, int y);
};
你的解决方案将按如下规则进行评判:
判题程序有一个由 CustomFunction 的 9 种实现组成的列表,以及一种为特定的 z 生成所有有效数对的答案的方法。
判题程序接受两个输入:function_id(决定使用哪种实现测试你的代码)以及目标结果 z 。
判题程序将会调用你实现的 findSolution 并将你的结果与答案进行比较。
如果你的结果与答案相符,那么解决方案将被视作正确答案,即 Accepted 。
示例 1:
输入:function_id = 1, z = 5
输出:[[1,4],[2,3],[3,2],[4,1]]
解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5
示例 2:
输入:function_id = 2, z = 5
输出:[[1,5],[5,1]]
解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5
提示:
1 <= function_id <= 9
1 <= z <= 100
题目保证 f(x, y) == z 的解处于 1 <= x, y <= 1000 的范围内。
在 1 <= x, y <= 1000 的前提下,题目保证 f(x, y) 是一个 32 位有符号整数。
解题思路一:双指针。首先我们不管f是什么,即function_id等于什么不管。但是我们可以调用customfunction中的f函数,然后我们遍历x,y(1 <= x, y <= 1000)只要f(x,y)=z的(x,y)即是我们需要的答案。然后我们从x=1与y=1000开始遍历。此时有三种情况:
- 情况一:f(x,y)>z,那么固定y,继续增大x,函数值也会继续增大。显然不符合题意。故将y减1缩小答案。
- 情况二:f(x,y)<z,那么固定y,继续增大x,函数值也会继续增大。显然是符合题意的。故将x加1增大答案。
- 情况三:f(x,y)=z,先将(x,y)加入答案,然后固定y,继续增大x,函数值也会继续增大。显然是不符合题意的。故将y减1缩小答案。(类似情况一)
/** // This is the custom function interface.* // You should not implement it, or speculate about its implementation* class CustomFunction {* public:* // Returns f(x, y) for any given positive integers x and y.* // Note that f(x, y) is increasing with respect to both x and y.* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)* int f(int x, int y);* };*/class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> ans;int x=1,y=1000;while(x<=1000&&y>=1){int t=customfunction.f(x,y);if(t>z) --y;else if(t<z) ++x;else ans.push_back({x++,y--});}return ans; }
};
时间复杂度:O(2C)//C=1000
空间复杂度:O(1)
解题思路二:二分查找。枚举x,二分查找y。找到之后x增大因为f对x,y递增故之后的y必小于middle。即f(x,middle)=z若要f(x+1,y)=z那么y必小于middle;对右边界的优化。
/** // This is the custom function interface.* // You should not implement it, or speculate about its implementation* class CustomFunction {* public:* // Returns f(x, y) for any given positive integers x and y.* // Note that f(x, y) is increasing with respect to both x and y.* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)* int f(int x, int y);* };*/class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;int left = 1, right = 1000;//右边界right会不断缩小for(int x=1;x<=1000;x++) {//枚举x,二分查找yleft = 1;//每次左边界left从1开始while(left<=right) {int middle=(left+right)/2;int t=customfunction.f(x, middle);if(t==z){res.push_back({x, middle});right=middle-1;//缩小右边界break;//break之后x增大因为f对x,y递增故之后的y必小于middle。即f(x,middle)=z若要f(x+1,y)=z那么y必小于middle;}else if(t<z) left=middle + 1;else right=middle-1;//缩小右边界}//其实发现 right == 0 了可以直接返回}return res;}
};
时间复杂度:O(C+logC)//C=1000
空间复杂度:O(1)
解题思路三:0
相关文章:

LeetCode-1237. 找出给定方程的正整数解【双指针,二分查找】
LeetCode-1237. 找出给定方程的正整数解【双指针,二分查找】题目描述:解题思路一:双指针。首先我们不管f是什么,即function_id等于什么不管。但是我们可以调用customfunction中的f函数,然后我们遍历x,y(1 < x, y &l…...

广度优先搜索算法 - 迷宫找路
广度优先搜索算法1 思考问题1.1 这个迷宫需不需要指定入口和出口?2 先粗略实现2.1 源码2.2 源码解释3 优化代码3.1 优化读取文件部分3.2 增加错误处理4 再优化-让程序变得更加灵活4.1 用户外部可以循环输入入口和出口5 完整代码这是一个提问者的提出的问题ÿ…...

泡脚材料简记
文章目录一般条件中药包(药粉)泡脚丸中药包(药材)艾叶生姜益母草藏红花食盐花椒白醋柠檬藿香泡脚私方紫苏叶、白术、白芍、黄芪、青皮、柴胡、夜交藤、丹参、当归,每种各10g艾叶、花椒、肉桂、桂枝、红花干姜30克、小茴…...
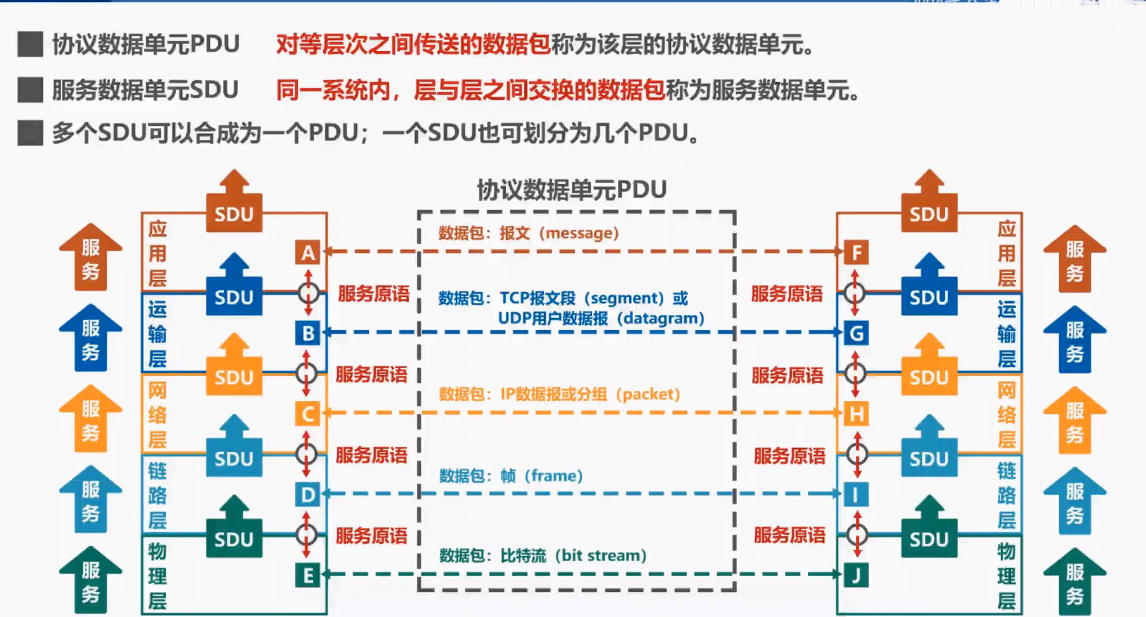
【计算机网络】因特网概述
文章目录因特网概述网络、互联网和因特网互联网历史与ISP标准化与RFC因特网的组成三种交换方式电路交换分组交换和报文交换三种交换方式的对比与总结计算机网络的定义和分类计算机网络的定义计算机网络的分类计算机网络的性能指标速率带宽吞吐量时延时延带宽积往返时间利用率丢…...

STC单片机 VS/HX1838红外接收和发送实验
STC单片机 VS/HX1838红外接收和发送实验 📌相关篇《STC单片机获取红外解码从串口输出》🔨所使用的红外接收头VS1838 📋VS1838引脚定义🌿5MM发射头,940nm红外发射二极管 红外遥控发射头。(外观看起来和普通的发光二极管没有什么差异,购买时需要注意确认)。 🔰采用的…...

前端开发常用案例(一)
前端开发常用案例1.实现三角形百度热榜样式分页效果小米商城自动轮播图效果二级下拉菜单效果时间轴效果展示音乐排行榜效果鼠标移入文字加载动画鼠标悬停缩放效果1.实现三角形 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8…...

Linux 日志查找常用命令
1.1 cat、zcat cat -n app.log | grep "error":查询日志中含有某个关键字error的信息,显示行号。 cat -n app.log | grep "error" --color:查询日志中含有某个关键字error的信息,显示行号,带颜色…...
CleanMyMac4.12.5最新版安装下载教程
告别硬盘空间不足,让您的Mac极速如新CleanMyMac是一款强大的 Mac 清理、加速工具和健康卫士,让您的 Mac 加快启动速度。CleanMyMac是一款专业的Mac清理软件,可智能清理mac磁盘垃圾和多余语言安装包,快速释放电脑内存,轻…...

RFID射频识别技术(四) RFID高频电路基础|课堂笔记|10月11日
2022年10月11日 week7 目录 第四讲: RFID高频电路基础 一、RLC(串联)电路的阻抗...
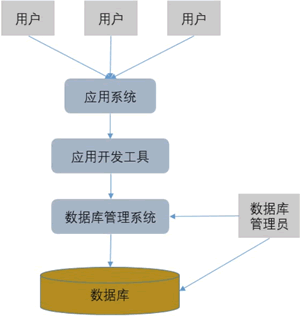
数据库系统是什么?它由哪几部分组成?
数据库系统(Database System,DBS)由硬件和软件共同构成。硬件主要用于存储数据库中的数据,包括计算机、存储设备等。软件部分主要包括数据库管理系统、支持数据库管理系统运行的操作系统,以及支持多种语言进行应用开发…...
)
华为OD机试题 - 任务混部(JavaScript)
最近更新的博客 2023新华为OD机试题 - 斗地主(JavaScript)2023新华为OD机试题 - 箱子之形摆放(JavaScript)2023新华为OD机试题 - 考古学家(JavaScript)2023新华为OD机试题 - 相同数字的积木游戏 1(JavaScript)2023新华为OD机试题 - 最多等和不相交连续子序列(JavaScri…...

键盘输入a,到屏幕显示,操作系统做了什么
首先,假定操作系统有中断系统。 等待的键盘写入的时候,txt进程被read函数阻塞。输入a之后,首先控制器,把扫描到的a放入到了控制器的寄存器中。触发硬中断通知cpu—> 中断IO控制方式,由硬件触发的。键盘读入中断cpu…...

Python机器学习入门笔记(2)—— 分类算法
目录 转换器(transformer)和估计器(estimator) K-近邻(K-Nearest Neighbors,简称KNN)算法 模型选择与调优 交叉验证(Cross-validation) GridSearchCV API 朴素贝叶…...

Docker镜像发布到阿里云和私有库
目录 一、Docker镜像 (一)概述 (二)Docker镜像加载原理 (三)镜像分层结构优势 (四)重点理解 (五)docker commit操作实例 (六)总…...
初识CSS,美化HTML
CSS称为:层叠样式表(Cascading style sheets)美化HTML即给页面种的HTML标签设置样式CSS语法规则css要写在head标签的里边,title标签的下面,用style标签框住<head> <title>...</title> <style>…...
)
华为OD机试 - 二维矩阵的最大值(Python)
题目二维矩阵的最大值 给定一个仅包含0和1的n*n二维矩阵 请计算二维矩阵的最大值 计算规则如下 每行元素按下标顺序组成一个二进制数(下标越大约排在低位), 二进制数的值就是该行的值,矩阵各行之和为矩阵的值允许通过向左或向右整体循环移动每个元素来改变元素在行中的位置 …...
)
华为OD机试 - 快递业务站(Python)
快递业务站 题目 快递业务范围有 N 个站点,A 站点与 B 站点可以中转快递,则认为 A-B 站可达, 如果 A-B 可达,B-C 可达,则 A-C 可达。 现在给 N 个站点编号 0、1、…n-1,用 s[i][j]表示 i-j 是否可达, s[i][j] = 1表示 i-j可达,s[i][j] = 0表示 i-j 不可达。 现用二维…...

百度沈抖:文心一言将通过百度智能云对外提供服务
2月17日,在2023 AI工业互联网高峰论坛上,百度智能云宣布“文心一言”将通过百度智能云对外提供服务,为产业带来AI普惠。 百度集团执行副总裁、百度智能云事业群总裁沈抖表示,“文心一言”是基于百度智能云技术打造出来的大模型&a…...

cmd 窗口、记事本打开后一片空白且几秒钟后闪退的问题解决方案汇总
前言 前段时间,电脑忽然出现了问题,首先是通过 微软应用商店 Microsoft Store 下载安装的 Snipaste 截图软件崩溃,不过将其卸载后,通过电脑管家下载后又可以正常使用了。 之后就是突然发现,记事本文本文档不能使用了…...

Linux 安装 SNMP服务
从安装盘IOS中导入安装SNMP. --挂载系统安装盘 [rootnb /]# mount -o loop -t iso9660 /software/radhat.iso /media mount: /dev/loop0 is write-protected, mounting read-only --导入安装包 [rootnb /]# rm -f /etc/yum.repos.d/*.repo [rootnbubackup /]# cat >/etc/yu…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

OpenHarmony标准系统-HDF框架之I2C驱动开发
文章目录 引言I2C基础知识概念和特性协议,四种信号组合 I2C调试手段硬件软件 HDF框架下的I2C设备驱动案例描述驱动Dispatch驱动读写 总结 引言 I2C基础知识 概念和特性 集成电路总线,由串网12C(1C、12C、Inter-Integrated Circuit BUS)行数据线SDA和串…...

汇编语言学习(三)——DoxBox中debug的使用
目录 一、安装DoxBox,并下载汇编工具(MASM文件) 二、debug是什么 三、debug中的命令 一、安装DoxBox,并下载汇编工具(MASM文件) 链接: https://pan.baidu.com/s/1IbyJj-JIkl_oMOJmkKiaGQ?pw…...
