华为OD机试 - 二维矩阵的最大值(Python)
题目二维矩阵的最大值
给定一个仅包含0和1的n*n二维矩阵
请计算二维矩阵的最大值
计算规则如下
- 每行元素按下标顺序组成一个二进制数(下标越大约排在低位),
二进制数的值就是该行的值,矩阵各行之和为矩阵的值 - 允许通过向左或向右整体循环移动每个元素来改变元素在行中的位置
比如
[1,0,1,1,1]向右整体循环移动两位[1,1,1,0,1]
二进制数为11101值为29
[1,0,1,1,1]向左整体循环移动两位[1,1,1,1,0]
二进制数为11110值为30
输入
- 数据的第一行为正整数,记录了 N 的大小,
0 < N <= 20 - 输入的第
2到n+1行为二维矩阵信息,行内元素边角逗号分割
输出描述
矩阵的最大值
示例一
输入
5
1,0,0,0,1
0,0,0,1,1
0,1,0,1,0
1,0,0,1,1
1,0,1,0,1
输出
122
相关文章:
)
华为OD机试 - 二维矩阵的最大值(Python)
题目二维矩阵的最大值 给定一个仅包含0和1的n*n二维矩阵 请计算二维矩阵的最大值 计算规则如下 每行元素按下标顺序组成一个二进制数(下标越大约排在低位), 二进制数的值就是该行的值,矩阵各行之和为矩阵的值允许通过向左或向右整体循环移动每个元素来改变元素在行中的位置 …...
)
华为OD机试 - 快递业务站(Python)
快递业务站 题目 快递业务范围有 N 个站点,A 站点与 B 站点可以中转快递,则认为 A-B 站可达, 如果 A-B 可达,B-C 可达,则 A-C 可达。 现在给 N 个站点编号 0、1、…n-1,用 s[i][j]表示 i-j 是否可达, s[i][j] = 1表示 i-j可达,s[i][j] = 0表示 i-j 不可达。 现用二维…...

百度沈抖:文心一言将通过百度智能云对外提供服务
2月17日,在2023 AI工业互联网高峰论坛上,百度智能云宣布“文心一言”将通过百度智能云对外提供服务,为产业带来AI普惠。 百度集团执行副总裁、百度智能云事业群总裁沈抖表示,“文心一言”是基于百度智能云技术打造出来的大模型&a…...

cmd 窗口、记事本打开后一片空白且几秒钟后闪退的问题解决方案汇总
前言 前段时间,电脑忽然出现了问题,首先是通过 微软应用商店 Microsoft Store 下载安装的 Snipaste 截图软件崩溃,不过将其卸载后,通过电脑管家下载后又可以正常使用了。 之后就是突然发现,记事本文本文档不能使用了…...

Linux 安装 SNMP服务
从安装盘IOS中导入安装SNMP. --挂载系统安装盘 [rootnb /]# mount -o loop -t iso9660 /software/radhat.iso /media mount: /dev/loop0 is write-protected, mounting read-only --导入安装包 [rootnb /]# rm -f /etc/yum.repos.d/*.repo [rootnbubackup /]# cat >/etc/yu…...
)
华为OD机试 - 滑动窗口最大和(Python)
滑动窗口最大和 有一个N个整数的数组,和一个长度为M的窗口。 窗口从数组内的第一个数开始滑动,直到窗口不能滑动为止。 每次滑动产生一个窗口,和窗口内所有数的和, 求窗口滑动产生的所有窗口和的最大值 输入 第一行输入一个正整数N,表示整数个数0 < N < 100000 …...
用Nacos搭建微服务操作
Nacos服务搭建 我们首先在Nacos的GitHub中下载相关的安装文件。https://github.com/alibaba/nacos/releases 但是因为服务器在国外,所以我们直接给大家提供了对应的安装文件。直接解压缩到非中文的目录下,然后启动即可 服务访问的地址是:htt…...

ChatGPT模型采样算法详解
ChatGPT模型采样算法详解 ChatGPT所使用的模型——GPT(Generative Pre-trained Transformer)模型有几个参数,理解它们对文本生成任务至关重要。其中最重要的一组参数是temperature和top_p。二者控制两种不同的采样技术,用于因果…...
【Unity3d】Unity与iOS通信
在unity开发或者sdk开发经常需要用到unity与oc之间进行交互,这里把它们之间通信代码整理出来。 Unity调用Objective-C 主要分三个步骤: (一)、在xcode中定义要被unity调用的函数 新建一个类,名字可以任意,比如UnityBridge&…...

RDD的持久化【博学谷学习记录】
RDD的缓存缓存: 一般当一个RDD的计算非常的耗时|昂贵(计算规则比较复杂),或者说这个RDD需要被重复(多方)使用,此时可以将这个RDD计算完的结果缓存起来, 便于后续的使用, 从而提升效率通过缓存也可以提升RDD的容错能力, 当后续计算失败后, 尽量不让RDD进行回溯所有的依赖链条, 从…...

Python3 正则表达式
Python3 正则表达式 正则表达式是一个特殊的字符序列,它能帮助你方便的检查一个字符串是否与某种模式匹配。 Python 自1.5版本起增加了re 模块,它提供 Perl 风格的正则表达式模式。 re 模块使 Python 语言拥有全部的正则表达式功能。 compile 函数根…...

Qt-基础
Qt1. 概念其他概念对话框模态对话框与非模态对话框事件事件拦截/过滤事件例子鼠标/屏幕使用界面功能qt-designer工具debug目录结构mainwindow控件窗口QMainWindow事件2. 项目概览QOBJECT tree 对象树3. 信号和槽信号函数关联自定义信号和槽函数自定义信号和槽函数1自定义信号和…...

ABB机器人将实时坐标发送给西门子PLC的具体方法示例
ABB机器人将实时坐标发送给西门子PLC的具体方法示例 本次以PROFINET通信为例进行说明,演示ABB机器人将实时坐标发送给西门子PLC的具体方法。 首先,要保证ABB机器人和PLC的信号地址分配已经完成,具体的内容可参考以下链接: S7-1200PLC与ABB机器人进行PROFINET通信的具体方法…...

反向传播与梯度下降详解
一,前向传播与反向传播 1.1,神经网络训练过程 神经网络训练过程是: 先通过随机参数“猜“一个结果(模型前向传播过程),这里称为预测结果 a a a;然后计算 a a a 与样本标签值...
Skywalking ui页面功能介绍
菜单栏 仪表盘:查看被监控服务的运行状态; 拓扑图:以拓扑图的方式展现服务之间的关系,并以此为入口查看相关信息; 追踪:以接口列表的方式展现,追踪接口内部调用过程; 性能剖析&am…...
哪里可以找到免费的 PDF 阅读编辑器?7 个免费 PDF 阅读编辑器分享
如果您曾经需要编辑 PDF,您可能会发现很难找到免费的 PDF 编辑器。幸运的是,您可以使用在线资源来编辑该文档,而无需为软件付费。 在本文中,我将介绍七种不同的 PDF 编辑器,它们至少可以让您免费编辑几个文件。我通过…...
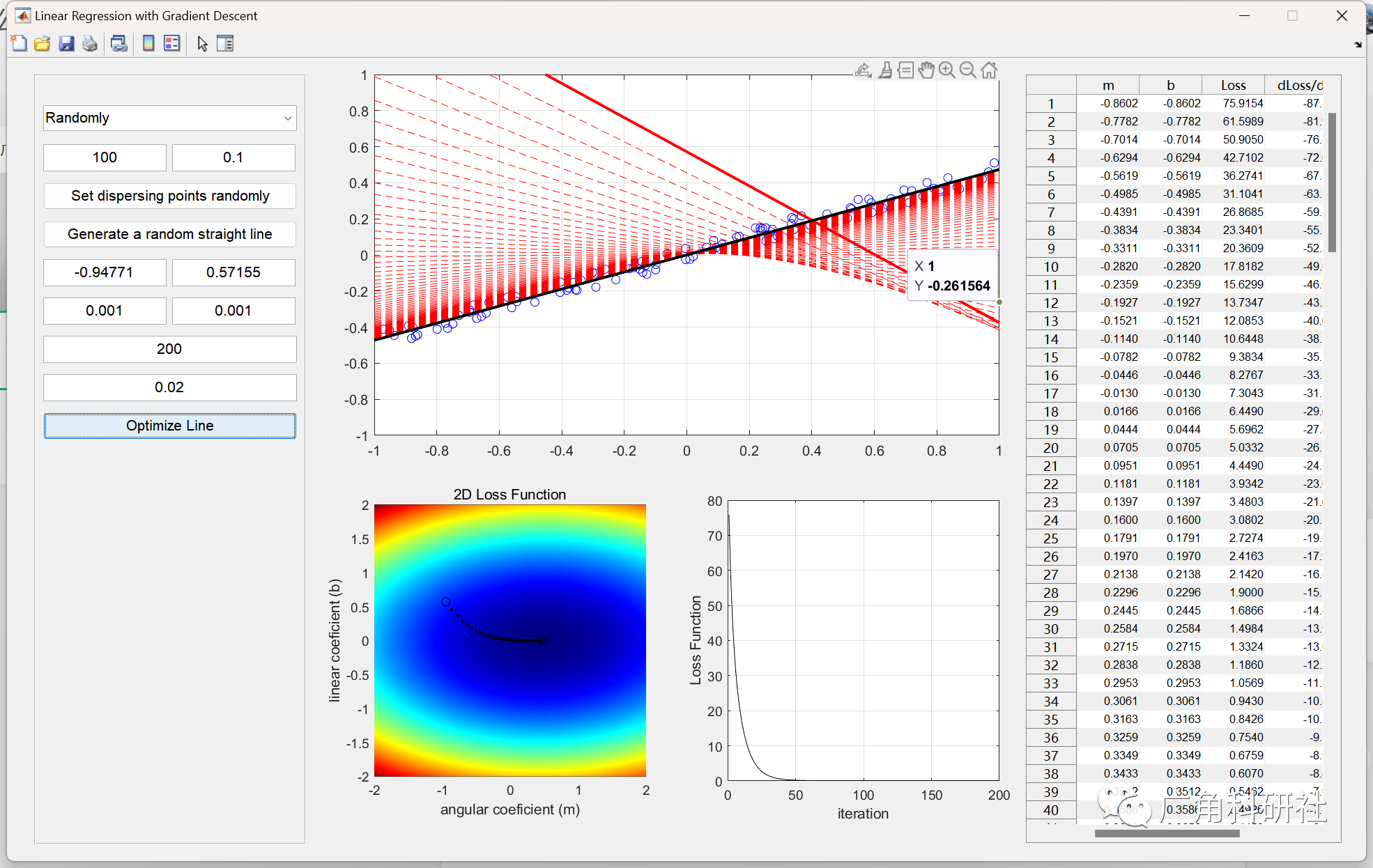
使用梯度下降的线性回归(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 梯度下降法,是一种基于搜索的最优化方法,最用是最小化一个损失函数。梯度下降是迭代法的一种,可以用于求…...
在Ubuntu上设置MySQL可以远程登录
在Ubuntu上设置MySQL可以远程登录一.设置数据库二.设置防火墙由于Ubuntu查看修改MySQL不是很方便,想着在虚拟机安装的Windows系统或者局域网中的其他电脑上去查看Ubuntu系统上的数据库,这样省事一些,我电脑安装的数据库是MySQL8。一.设置数据…...
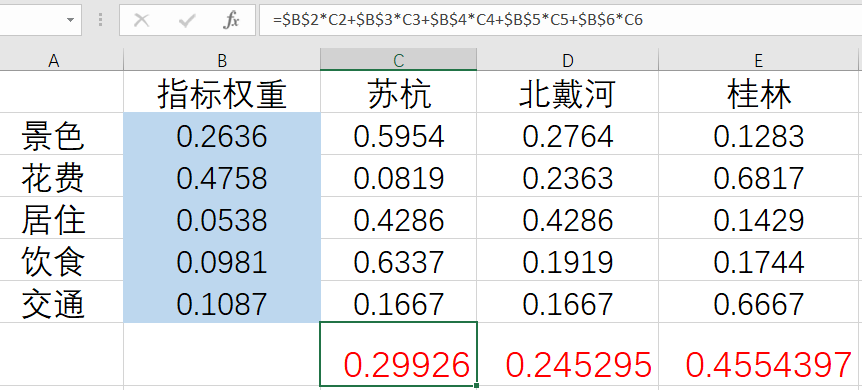
清风1.层次分析法
一.流程1.建立评价体系2.建立判断矩阵2.1 A-C-C矩阵从准则层对目标层的特征向量上看,花费的权重最大算术平均法求权重的结果为:0.26230.47440.05450.09850.1103几何平均法求权重的结果为:0.26360.47730.05310.09880.1072特征值法求权重的结果…...

「首席架构师推荐」免费数据可视化软件你喜欢哪一个?
数据可视化,是关于数据视觉表现形式的科学技术研究。其中,这种数据的视觉表现形式被定义为,一种以某种概要形式抽提出来的信息,包括相应信息单位的各种属性和变量。它是一个处于不断演变之中的概念,其边界在不断地扩大…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
