反向传播与梯度下降详解
相关文章:

反向传播与梯度下降详解
一,前向传播与反向传播 1.1,神经网络训练过程 神经网络训练过程是: 先通过随机参数“猜“一个结果(模型前向传播过程),这里称为预测结果 a a a;然后计算 a a a 与样本标签值...
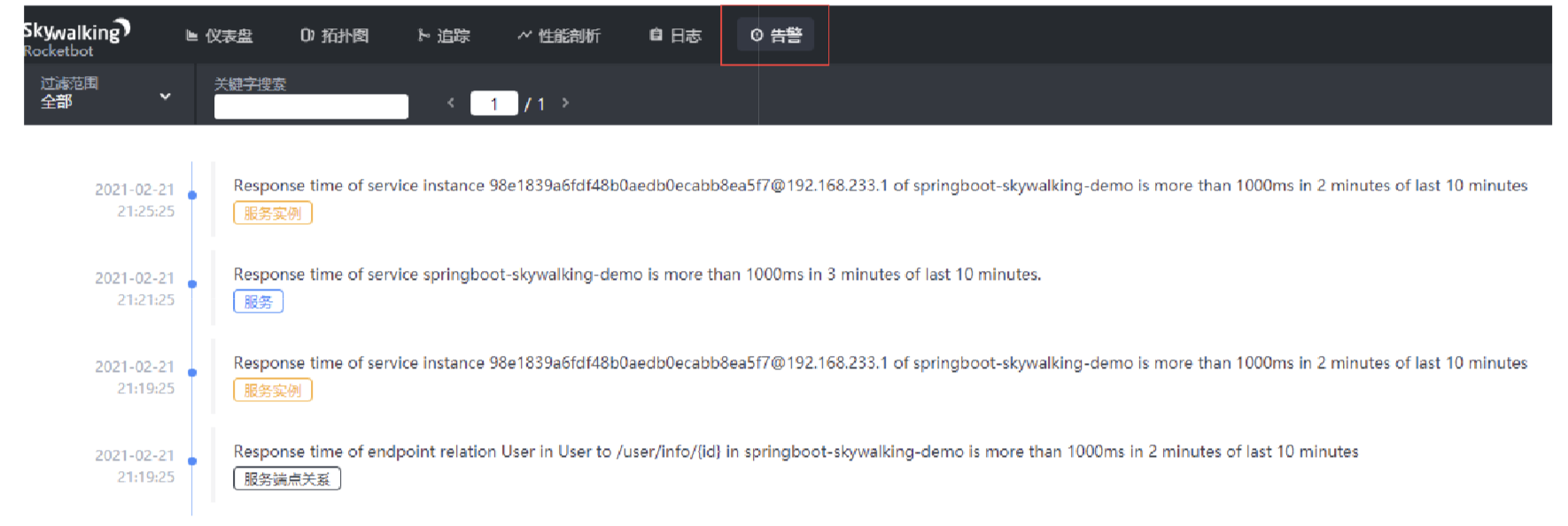
Skywalking ui页面功能介绍
菜单栏 仪表盘:查看被监控服务的运行状态; 拓扑图:以拓扑图的方式展现服务之间的关系,并以此为入口查看相关信息; 追踪:以接口列表的方式展现,追踪接口内部调用过程; 性能剖析&am…...
哪里可以找到免费的 PDF 阅读编辑器?7 个免费 PDF 阅读编辑器分享
如果您曾经需要编辑 PDF,您可能会发现很难找到免费的 PDF 编辑器。幸运的是,您可以使用在线资源来编辑该文档,而无需为软件付费。 在本文中,我将介绍七种不同的 PDF 编辑器,它们至少可以让您免费编辑几个文件。我通过…...
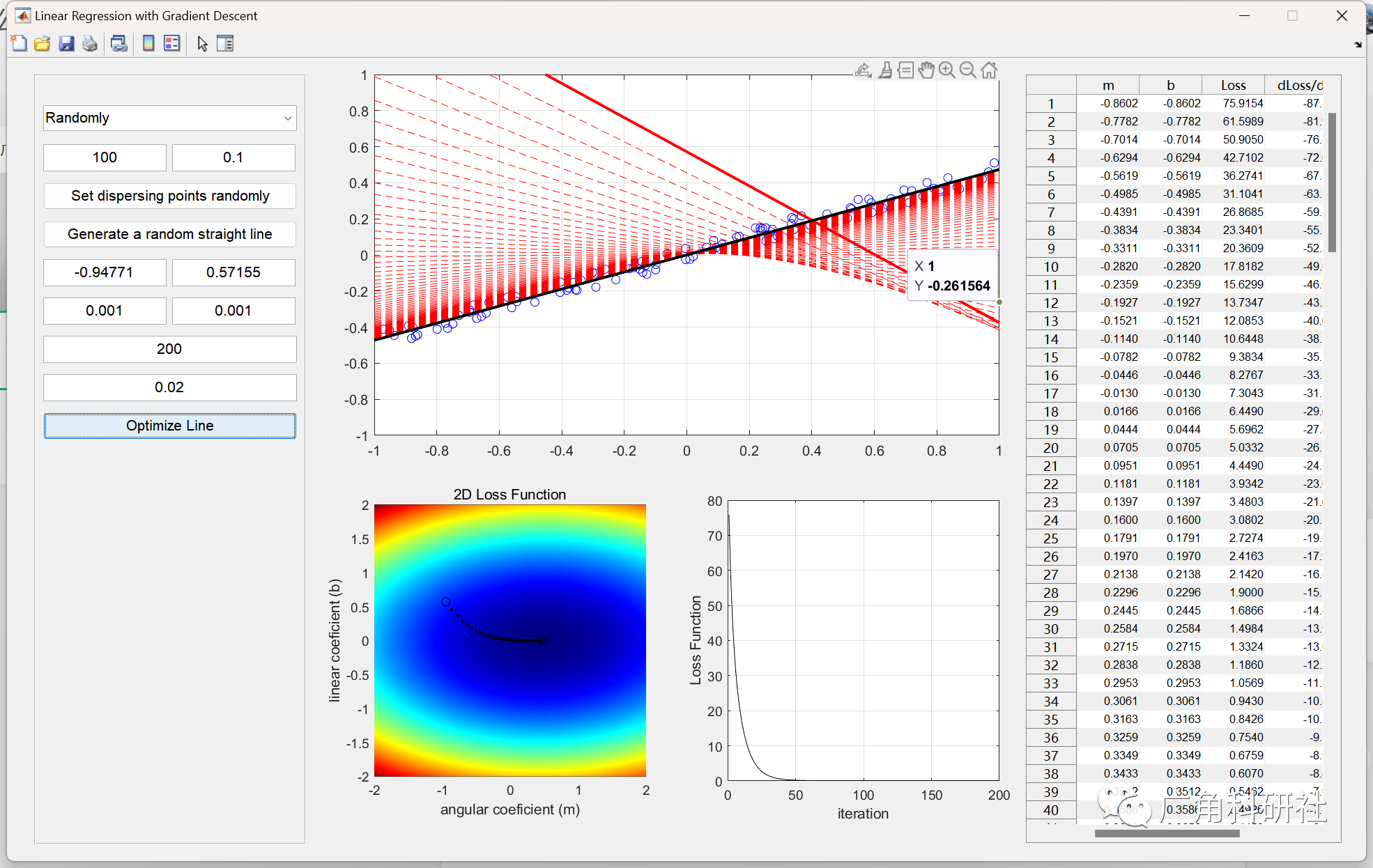
使用梯度下降的线性回归(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 梯度下降法,是一种基于搜索的最优化方法,最用是最小化一个损失函数。梯度下降是迭代法的一种,可以用于求…...
在Ubuntu上设置MySQL可以远程登录
在Ubuntu上设置MySQL可以远程登录一.设置数据库二.设置防火墙由于Ubuntu查看修改MySQL不是很方便,想着在虚拟机安装的Windows系统或者局域网中的其他电脑上去查看Ubuntu系统上的数据库,这样省事一些,我电脑安装的数据库是MySQL8。一.设置数据…...
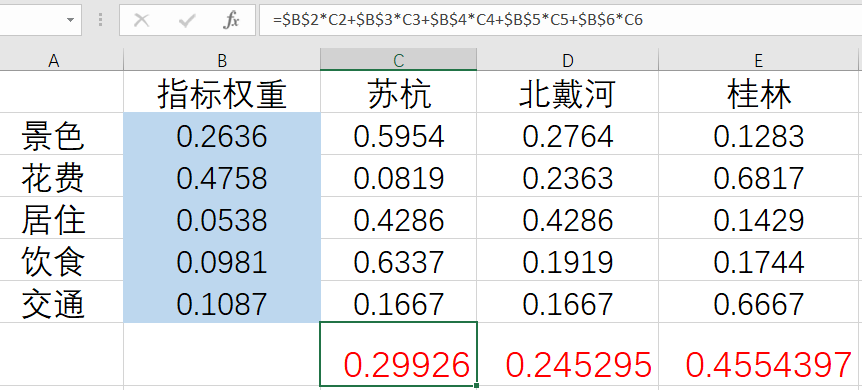
清风1.层次分析法
一.流程1.建立评价体系2.建立判断矩阵2.1 A-C-C矩阵从准则层对目标层的特征向量上看,花费的权重最大算术平均法求权重的结果为:0.26230.47440.05450.09850.1103几何平均法求权重的结果为:0.26360.47730.05310.09880.1072特征值法求权重的结果…...

「首席架构师推荐」免费数据可视化软件你喜欢哪一个?
数据可视化,是关于数据视觉表现形式的科学技术研究。其中,这种数据的视觉表现形式被定义为,一种以某种概要形式抽提出来的信息,包括相应信息单位的各种属性和变量。它是一个处于不断演变之中的概念,其边界在不断地扩大…...

深度学习术语解释:backbone、head、neck,etc
backbone:翻译为主干网络的意思,既然说是主干网络,就代表其是网络的一部分,那么是哪部分呢?这个主干网络大多时候指的是提取特征的网络,其作用就是提取图片中的信息,共后面的网络使用。这些网络…...
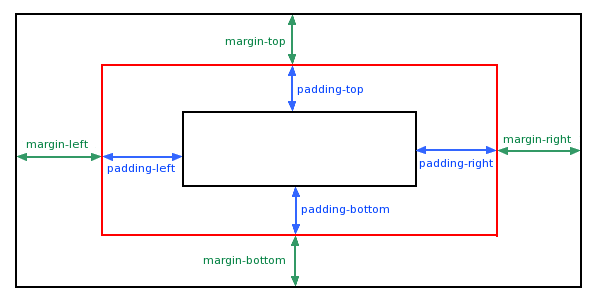
基础篇—CSS margin(外边距)解析
什么是CSS margin(外边距)? CSS margin(外边距)属性定义元素周围的空间。 属性描述margin简写属性。在一个声明中设置所有外边距属性。margin-bottom设置元素的下外边距。margin-left设置元素的左外边距。margin-right设置元素的右外边距。margin-top设置元素的上外边距。mar…...

ChatGPT或将引发新一轮失业潮?是真的吗?
最近,要说有什么热度不减的话题,那ChatGPT必然榜上有名。据悉是这是由美国人工智能研究实验室OpenAI开发的一种全新聊天机器人模型,它能够通过学习和理解人类的语言来进行对话,还能根据聊天的上下文进行互动,并协助人类…...
【Selenium学习】Selenium 中特殊元素操作
1.鼠标定位操作鼠标悬停,即当光标与其名称表示的元素重叠时触发的事件,在 Selenium 中将键盘鼠标操作封装在 Action Chains 类中。Action Chains 类的主要应用场景为单击鼠标、双击鼠标、鼠标拖曳等。部分常用的方法使用分类如下:• click(on…...

Spark相关的依赖冲突,后期持续更新总结
Spark相关的依赖冲突持续更新总结 Spark-Hive_2.11依赖报错 这个依赖是Spark开启支持hive SQL解析,其中2.11是Spark对应的Scala版本,如Spark2.4.7,对应的Scala版本是2.11.12;这个依赖会由于Spark内部调用的依赖guava的版本问题出…...

【每日一题Day122】LC1237找出给定方程的正整数解 | 双指针 二分查找
找出给定方程的正整数解【LC1237】 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知,但它是单调递增函数&#…...
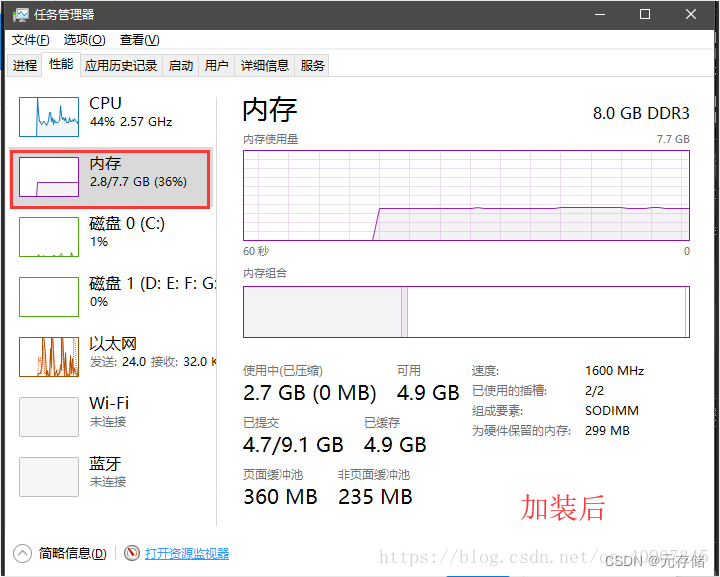
笔记本加装固态和内存条教程(超详细)
由于笔记本是几年前买的了,当时是4000,现在用起来感到卡顿,启动、运行速度特别慢,就决定换个固态硬盘,加个内存条,再给笔记本续命几年。先说一下加固态硬盘SSD的好处:1.启动快 2.读取延迟小 3.写…...

【Python】字典 - Dictionary
字典 - Dictionarykeys()values()items()get()获取文件中指定字符的个数进阶版:获取所有单词的频数进阶版:获取所有字符的频数函数内容keys()输出字典中的所有键values()输出字典中的所有值items()以元组的形式输出键值对get()获取字典中指定键的值 keys…...
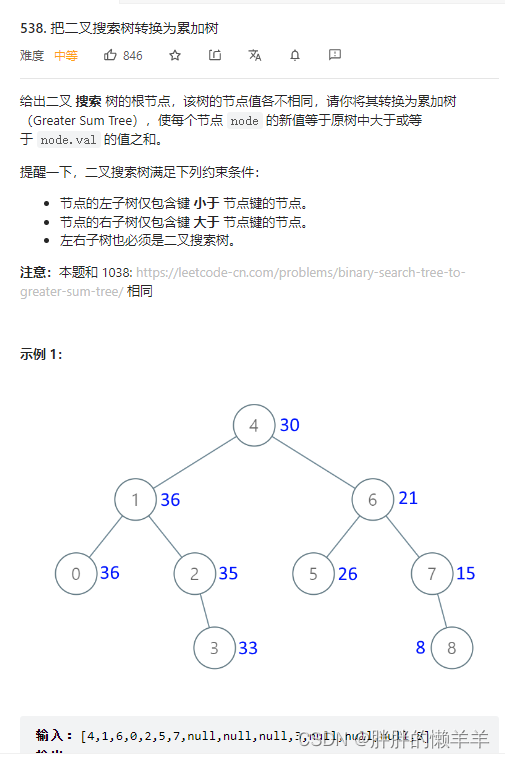
LeetCode分类刷题----二叉树
二叉树1.二叉树的递归遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历2.二叉树的迭代遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历3.二叉树的层序遍历102.二叉树的层序遍历107.二叉树的层序遍历||199.二叉树的右视图637.二叉树的层平均…...
)
Zipkin : Golang 微服务全链路监控(三)
Zipkin : Golang 微服务全链路监控(三) Golang 微服务全链路监控实现 broker-service -> auth-service -> postgres dbzipkin 监控:需代码入侵 使用 zipkin 库的 serverMiddleware,其通过 Http 跟踪(trace&am…...
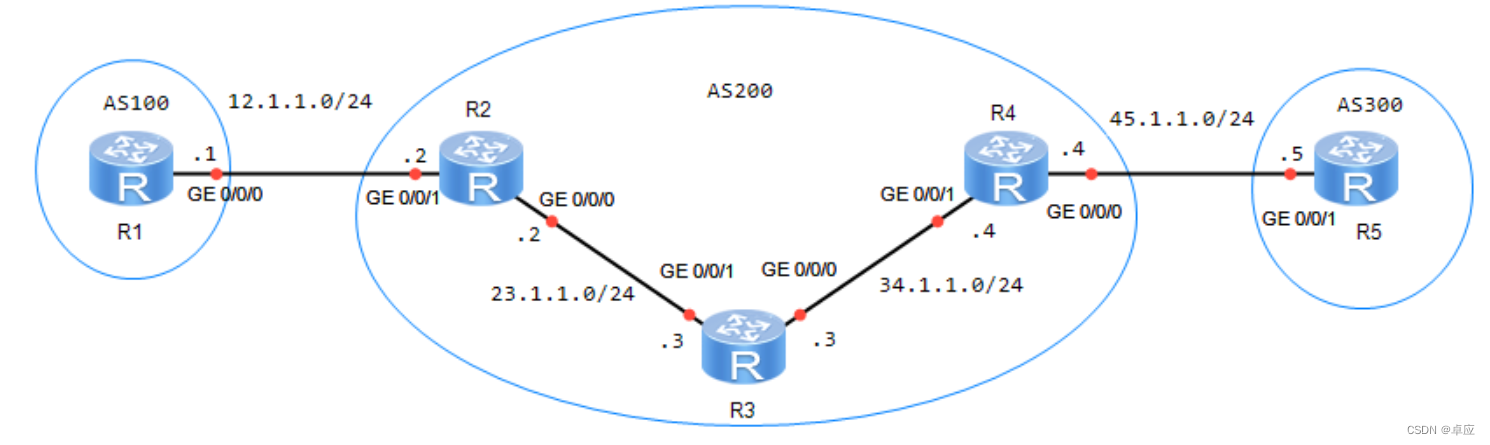
5.3 BGP路由黑洞
5.2.3实验3:BGP路由黑洞 1. 实验目的 熟悉BGP路由黑洞的应用场景掌握BGP水平分割的配置方法2. 实验拓扑 实验拓扑如图5-3所示: 图5-3:BGP路由黑洞 3. 实验步骤 配置IP地址 R1的配置 <Huawei>syst...
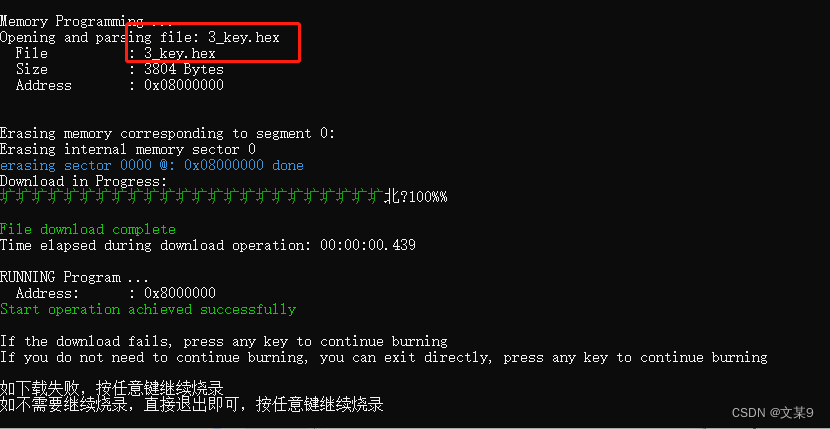
STM32 DFU模式烧录代码
什么是DFU? dfu的本质是isp,usb接口的isp,在系统编程,进入isp的方式我们先了解 如下图 boot0为高电平 boot1为低电平即可进入isp模式。 熟悉的场景 在我们使用flymcu软件下载代码时,本质也是isp 串口接口的isp。 傻瓜使用方式…...
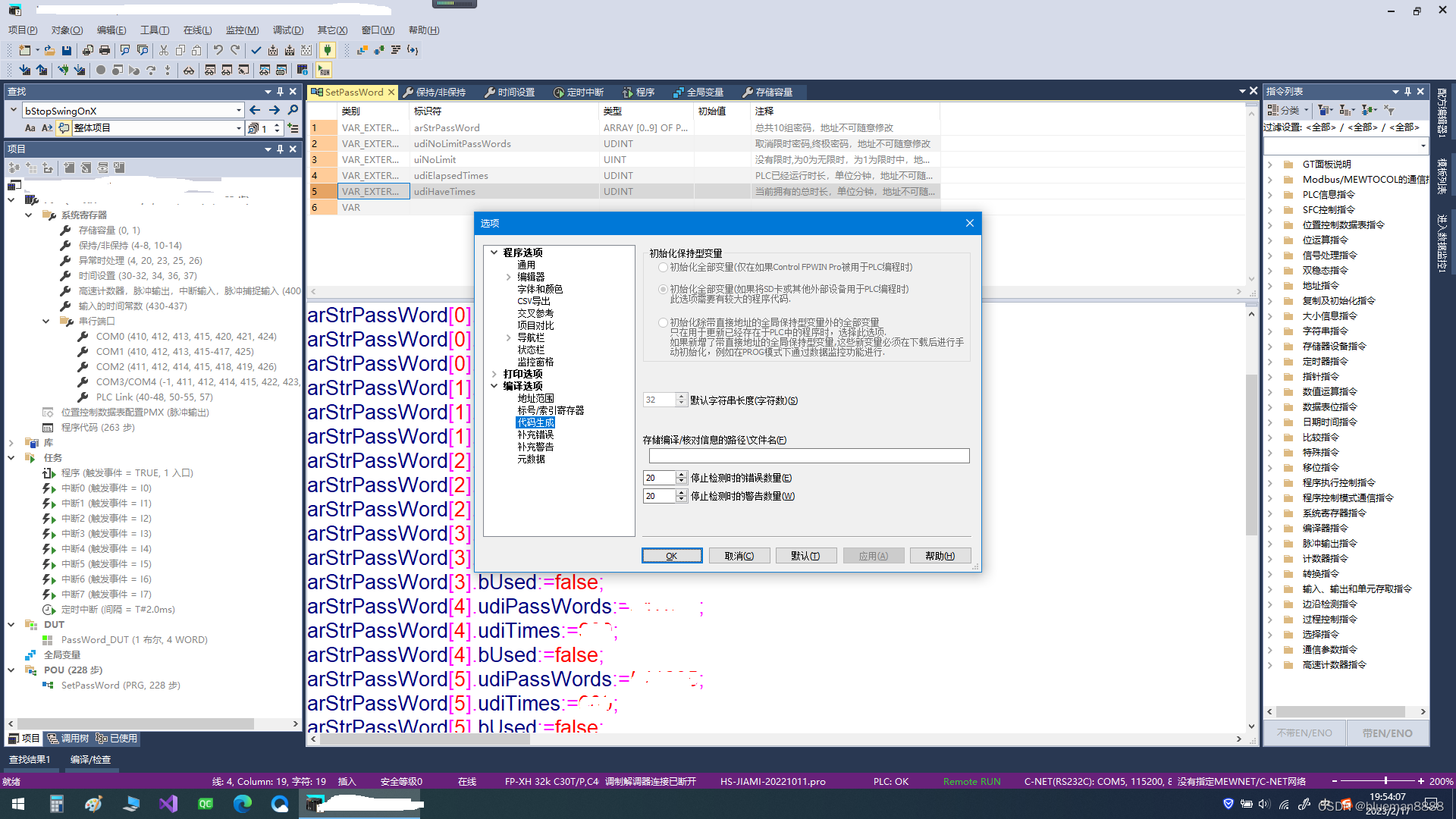
松下PLC通过fpwin上传写入MRTC模块方法
目录 PLC程序上传方法 加密模块使用 PLC程序上传方法 手动将PLC模式设置为prog模式查看PLC是否设置为禁止上传查询指示灯是否变蓝,变蓝则需要将PLC禁止上传功能取消。 3.当上述动作操作完成后,将PLC程序导入到PLC中。为了配合加密程序使用,…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
