c++基本数据结构
void insert(const node *head, node *p)
{node *x, *y;y=head;do{x=y;y=x->next;} while ((y!=NULL) && (y->value < p->value);x->next=p;p->next=y;
}
二.栈
(1) 栈的实现!
操作规则:先进后出,先出后进。
int stack[N], top=0; // top表示栈顶位置。
入栈:inline void push(int a) { stack[top++]=a; }
出栈:inline int pop() { return stack[--top];
栈空的条件:inline bool empty() { return top<0; }
如果两个栈有相反的需求,可以用这种方法节省空间:用一个数组表示两个栈。分别用top1、top2表示栈顶的位置,令top1从0开始,top2从N-1开始。
(2) DFS和栈
递归其实也用到了栈。每调用一次函数,都相当于入栈(当然这步操作“隐藏在幕后”)。函数调用完成,相当于出栈。
一般情况下,调用栈的空间大小为16MB。也就是说,如果递归次数太多,很容易因为栈溢出导致程序崩溃,即“爆栈”。
为了防止“爆栈”,可以将递归用栈显式实现。如果可行,也可以改成迭代、递推等方法。
使用栈模拟递归时,注意入栈的顺序——逆序入栈,后递归的要先入栈,先递归的要后入栈。
下面是非递归版本的DFS模板:
stack <int> s; // 存储状态
void DFS(int v, …)
{s.push(v); // 初始状态入栈while (!s.empty()){int x = s.top(); s.pop(); // 获取状态// 处理结点if (x达到某种条件){// 输出、解的数量加1、更新目前搜索到的最优值等…return;}// 寻找下一状态。当然,不是所有的搜索都要这样寻找状态。// 注意,这里寻找状态的顺序要与递归版本的顺序相反,即逆序入栈。for (i=n-1;i>=0;i--){s.push(… /*i对应的状态*/);}}// 无解cout<<"No Solution.";
}
三.队列
(1) 顺序队列
操作规则:先进先出,后进后出。
定义:int queue[N], front=0, rear=0;
front指向队列首个元素,rear指向队列尾部元素的右侧。
入队:inline void push(int a) { queue[rear++]=a; }
出队:inline int pop() { return queue[front++]; }
队空的条件:inline bool empty() { return front==rear; }
(2) 循环队列
循环队列——把链状的队列变成了一个环状队列。与上面的链状队列相比,可以节省很大空间。
定义:int queue[N], front=0, rear=0;
front指向队列首个元素,rear指向队列尾部元素的右侧。
入队:inline void push(int a) { queue[rear]=a; rear=(rear+1)%N; }
出队:inline int pop() { int t=queue[front]; front=(front+1)%N; return t; }
队满或队空的条件:inline bool empty() { return front==rear; }
队满和队空都符合上述条件。怎么把它们区分开呢?
第一种方法:令队列的大小是N+1,然后只使用N个元素。这样队满和队空的条件就不一样了。
第二种方法:在入队和出队同时记录队列元素个数。这样,直接检查元素个数就能知道队列是空还是满。
(3) BFS和队列
BFS要借助队列来完成,并且,将队列改成堆栈,BFS就变成了DFS。BFS的具体实现见42页“3.7 代码模板”。
四.二叉树
(1) 二叉树的链表存储法
struct node
{int value;node *leftchild, *rightchild;//int id; // 结点编号。//node *parent; // 指向父亲结点。
} arr[N];
int top=-1;
node * head = NULL;
#define NEW(p) p=&arr[++top]; p->leftchild=NULL; \p->rightchild=NULL; p->value=0
(2) 完全二叉树的一维数组存储法
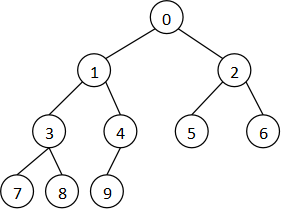
如果一个二叉树的结点严格按照从上到下、从左到右的顺序填充,就可以用一个一维数组保存。
下面假设这个树有n个结点,待操作的结点是r(0≤r<n)。
| 操作 | 宏定义 | r的取值范围 |
| r的父亲 | #define parent(r) (((r)-1)/2) | r≠0 |
| r的左儿子 | #define leftchild(r) ((r)*2+1) | 2r+1<n |
| r的右儿子 | #define rightchild(r) ((r)*2+2) | 2r+2<n |
| r的左兄弟 | #define leftsibling(r) ((r)-1) | r为偶数且0<r≤n-1 |
| r的右兄弟 | #define rightsibling(r) ((r)+1) | r为奇数且r+1<n |
| 判断r是否为叶子 | #define isleaf(r) ((r)>=n/2) | r<n |
(3) 二叉树的遍历
1. 前序遍历
void preorder(node *p)
{if (p==NULL) return;// 处理结点pcout<<p->value<<' ';preorder(p->leftchild);preorder(p->rightchild);
}
2. 中序遍历
void inorder(node *p)
{if (p==NULL) return;inorder(p->leftchild);// 处理结点pcout<<p->value<<' ';inorder(p->rightchild);
}
3. 后序遍历
void postorder(node *p)
{if (p==NULL) return;postorder(p->leftchild);postorder(p->rightchild);// 处理结点pcout<<p->value<<' ';
}
假如二叉树是通过动态内存分配建立起来的,在释放内存空间时应该使用后序遍历。
4. 宽度优先遍历(BFS)
首先访问根结点,然后逐个访问第一层的结点,接下来逐个访问第二层的结点……
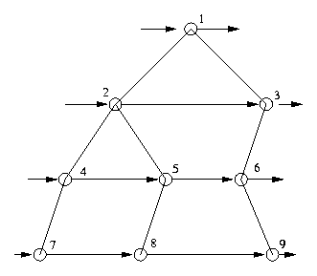
node *q[N];
void BFS(node *p)
{if (p==NULL) return;int front=1,rear=2;q[1]=p;while (front<rear){node *t = q[front++];// 处理结点tcout<<t->value<<' ';if (t->leftchild!=NULL) q[rear++]=t->leftchild;if (t->rightchild!=NULL) q[rear++]=t->rightchild;}
}
对于完全二叉树,可以直接遍历:
for (int i=0; i<n; i++) cout<<a[i]<<' ';
(4) 二叉树重建
【问题描述】二叉树的遍历方式有三种:前序遍历、中序遍历和后序遍历。现在给出其中两种遍历的结果,请输出第三种遍历的结果。
【分析】
前序遍历的第一个元素是根,后序遍历的最后一个元素也是根。所以处理时需要到中序遍历中找根,然后递归求出树。
注意!输出之前须保证字符串的最后一个字符是'\0'。
1. 中序+后序→前序
void preorder(int n, char *pre, char *in, char *post)
{if (n<=0) return;int p=strchr(in, post[n-1])-in;pre[0]=post[n-1];preorder(p, pre+1, in, post);preorder(n-p-1, pre+p+1, in+p+1, post+p);
}
2. 前序+中序→后序
void postorder(int n, char *pre, char *in, char *post)
{if (n<=0) return;int p=strchr(in, pre[0])-in;postorder(p, pre+1, in, post);postorder(n-p-1, pre+p+1, in+p+1, post+p);post[n-1]=pre[0];
}
3. 前序+后序→中序
“中+前”和“中+后”都能产生唯一解,但是“前+后”有多组解。下面输出其中一种。
bool check(int n, char *pre, char *post) // 判断pre、post是否属于同一棵二叉树
{bool b;for (int i=0; i<n; i++){b=false;for (int j=0; j<n; j++)if (pre[i]==post[j]){b=true;break;}if (!b) return false;}return true;
}void inorder(int n, char *pre, char *in, char *post)
{if (n<=0) return;int p=1;while (check(p, pre+1, post)==false && p<n)p++;if (p>=n) p=n-1; // 此时,如果再往inorder里传p,pre已经不含有效字符了。inorder(p, pre+1, in, post);in[p]=pre[0];inorder(n-p-1, pre+p+1, in+p+1, post+p);
}
(5) 求二叉树的直径*
从任意一点出发,搜索距离它最远的点,则这个最远点必定在树的直径上。再搜索这个最远点的最远点,这两个最远点的距离即为二叉树的直径。
求树、图(连通图)的直径的思想是相同的。
// 结点编号从1开始,共n个结点。
struct node
{int v;node *parent, *leftchild, *rightchild;
} a[1001], *p;
int maxd;
bool T[1003];
#define t(x) T[((x)==NULL)?0:((x)-a+1)]
node *p;
void DFS(node * x, int l)
{if (l>maxd) maxd=l, p=x;if (x==NULL) return;t(x)=false;if (t(x->parent)) DFS(x->parent, l+1);if (t(x->leftchild)) DFS(x->leftchild, l+1);if (t(x->rightchild)) DFS(x->rightchild, l+1);
}int distance(node *tree) // tree已经事先读好
{maxd=0;memset(T, 0, sizeof(T));for (int i=1; i<=n; i++)T[i]=true;DFS(tree,0);maxd=0;memset(T, 0, sizeof(T));for (int i=1; i<=n; i++) T[i]=true;DFS(p,0);return maxd;
}
五.并查集
并查集最擅长做的事情——将两个元素合并到同一集合、判断两个元素是否在同一集合中。
并查集用到了树的父结点表示法。在并查集中,每个元素都保存自己的父亲结点的编号,如果自己就是根结点,那么父亲结点就是自己。这样就可以用树形结构把在同一集合的点连接到一起了。
并查集的实现:
struct node
{int parent; // 表示父亲结点。当编号i==parent时为根结点。int count; // 当且仅当为根结点时有意义:表示自己及子树元素的个数int value; // 结点的值
} set[N];int Find(int x) // 查找算法的递归版本(建议不用这个)
{return (set[x].parent==x) ? x : (set[x].parent = Find(set[x].parent));
}int Find(int x) // 查找算法的非递归版本
{int y=x;while (set[y].parent != y) // 寻找父亲结点y = set[y].parent;while (x!=y) // 路径压缩,即把途中经过的结点的父亲全部改成y。{int temp = set[x].parent;set[x].parent = y;x = temp;}return y;
}void Union(int x, int y) // 小写的union是关键字。
{x=Find(x); y=Find(y); // 寻找各自的根结点if (x==y) return; // 如果不在同一个集合,合并if (set[x].count > set[y].count) // 启发式合并,使树的高度尽量小一些{set[y].parent = x;set[x].count += set[y].count;}else{set[x].parent = y;set[y].count += set[x].count;}
}void Init(int cnt) // 初始化并查集,cnt是元素个数
{for (int i=1; i<=cnt; i++){set[i].parent=i;set[i].count=1;set[i].value=0;}
}void compress(int cnt) // 合并结束,再进行一次路径压缩
{for (int i=1; i<=cnt; i++) Find(i);
}
说明:
使用之前调用Init()!
Union(x,y):把x和y进行启发式合并,即让节点数比较多的那棵树作为“树根”,以降低层次。
Find(x):寻找x所在树的根结点。Find的时候,顺便进行了路径压缩。
上面的Find有两个版本,一个是递归的,另一个是非递归的。
判断x和y是否在同一集合:if (Find(x)==Find(y)) ……
在所有的合并操作结束后,应该执行compress()。
并查集的效率很高,执行m次查找的时间约为O(5m)。
六.总结
数据结构是计算机科学的重要分支。选择合适的数据结构,可以简化问题,减少时间的浪费。
1. 线性表
线性表有两种存储方式,一种是顺序存储,另一种是链式存储。前者只需用一维数组实现,而后者既可以用数组实现,又可以用指针实现。
顺序表的特点是占用空间较小,查找和定位的速度很快,但是插入和删除元素的速度很慢(在尾部速度快);链表和顺序表正好相反,它的元素插入和删除速度很快,但是查找和定位的速度很慢(同样,在首尾速度快)。
2. 栈和队列
栈和队列以线性表为基础。它们的共同点是添加、删除元素都有固定顺序,不同点是删除元素的顺序。队列从表头删除元素,而栈从表尾删除元素,所以说队列是先进先出表,堆栈是先进后出表。
栈和队列在搜索中有非常重要的应用。栈可以用来模拟深度优先搜索,而广度优先搜索必须用队列实现。
有时为了节省空间,栈的两头都会被利用,而队列会被改造成循环队列。
3. 二叉树
上面几种数据结构都是线性结构。而二叉树是一种很有用的非线性结构。二叉树可以采用以下的递归定义:二叉树要么为空,要么由根结点、左子树和右子树组成。左子树和右子树分别是一棵二叉树。
计算机中的树和现实生活不同——计算机里的树是倒置的,根在上,叶子在下。
完全二叉树:一个完全二叉树的结点是从上到下、从左到右地填充的。如果高度为h,那么0~h-1层一定已经填满,而第h层一定是从左到右连续填充的。
通常情况下,二叉树用指针实现。对于完全二叉树,可以用一维数组实现(事先从0开始编号)。
访问二叉树的所有结点的过程叫做二叉树的遍历。常用的遍历方式有前序遍历、中序遍历、后序遍历,它们都是递归完成的。
4. 树
树也可以采用递归定义:树要么为空,要么由根结点和n(n≥0)棵子树组成。
森林由m(m≥0)棵树组成。
二叉树不是树的一种,因为二叉树的子树中有严格的左右之分,而树没有。这样,树可以用父结点表示法来表示(当然,森林也可以)。并查集的合并、查询速度很快,它就是用父结点表示法实现的。
不过父结点表示法的遍历比较困难,所以常用“左儿子右兄弟”表示法把树转化成二叉树。
树的遍历和二叉树的遍历类似,不过不用中序遍历。它们都是递归结构,所以可以在上面实施动态规划。
树作为一种特殊的图,在图论中也有广泛应用。
树的表示方法有很多种。
第一种是父节点表示法,它适合并查算法,但不便遍历。
第二种是子节点表表示法。
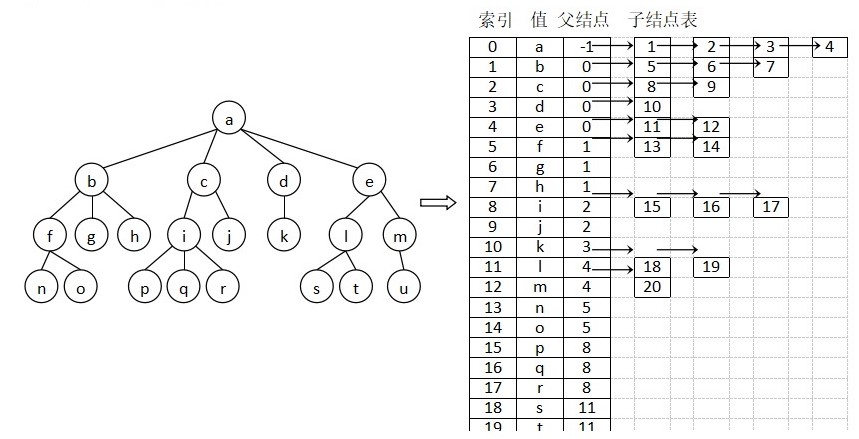
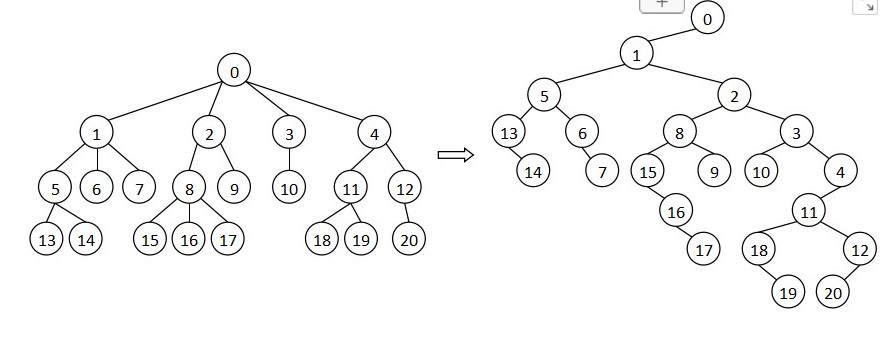
第三种是“左儿子右兄弟”表示法。
相关文章:

c++基本数据结构
void insert(const node *head, node *p) {node *x, *y;yhead;do{xy;yx->next;} while ((y!NULL) && (y->value < p->value);x->nextp;p->nexty; } 二.栈 (1) 栈的实现! 操作规则:先进后出,先出后进。 int stack[N], top0; /…...
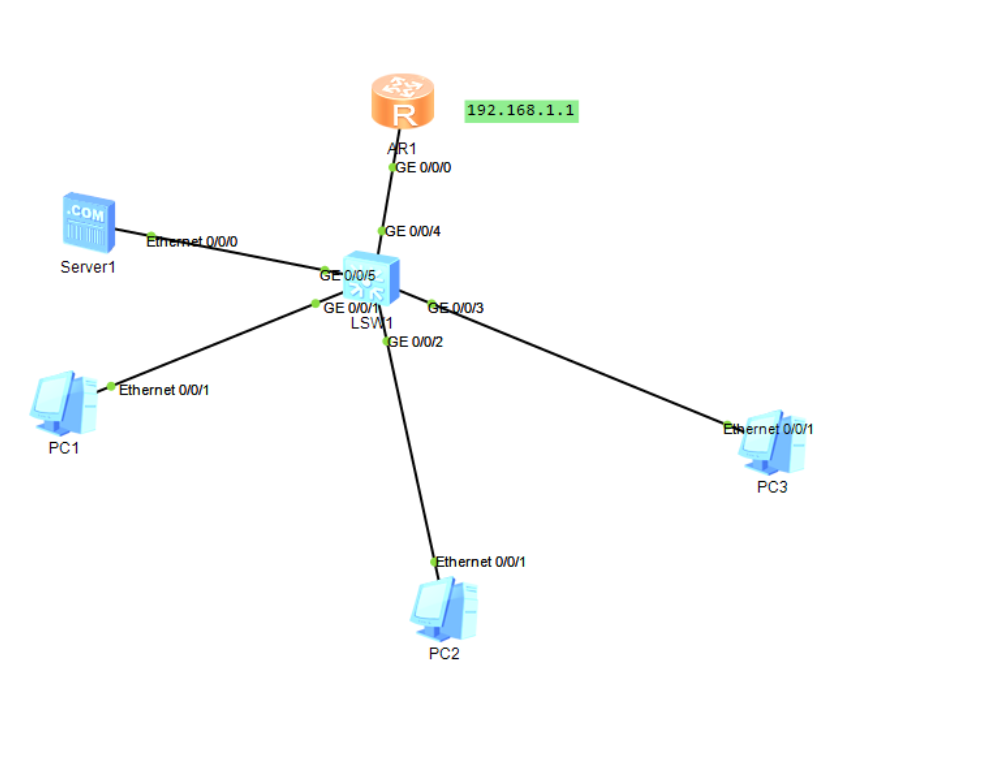
路由器DHCP实验
拓扑图 配置 # 配置ip地址并开启dhcp [Huawei]int g0/0/0 [Huawei-GigabitEthernet0/0/0]ip addr 192.168.1.1 255.255.255.0 [Huawei-GigabitEthernet0/0/0]dhcp enable## 配置dns地址 [Huawei-GigabitEthernet0/0/0]dhcp dns-list 192.168.1.5## 指定某个接口开通DHCP 功能…...

Linux 电源子系统之充电、放电、低功耗
在嵌入式产品中,有三个重要模块:充电、放电、低功耗。 1、充电 charging 1、开关电源基本原理 2、线性充电和开关电源硬件电路图分析 3、Battery_Charging_v1.2 spec 4、typec spec 5、typec-PD spec 6、Uevent 在 Android 层的实现 7、battery service 监听 uevent 事件以…...

捕捉时刻:将PDF文件中的图像提取为个性化的瑰宝(从pdf提取图像)
应用场景: 该功能的用途是从PDF文件中提取图像。这在以下情况下可能会很有用: 图片提取和转换:可能需要将PDF文件中的图像提取出来,并保存为单独的图像文件,以便在其他应用程序中使用或进行进一步处理。例如ÿ…...

【基础类】—HTTP协议类
一、HTTP协议的主要特点 简单快速:每个资源URI是固定的,访问某个资源输入URI即可灵活:在每一个HTTP协议中,请求头部分有一个数据类型,通过一个HTTP协议可以完成不同的数据类型传输无连接:连接一次就会断开…...

【Qt高级】QThread与QTimer组合使用引出的信号槽执行在哪个线程的思考【2023.08.06】
源码见 testQThread_QTimer… Qt 版本5.6.3 视频讲解:https://www.bilibili.com/video/BV15P411C79i/ 链接: 视频讲解 简介 想法很单纯,就是主线程启动一个子线程,子线程里启动一个定时器,定时执行一些任务,然鹅实际开…...
用于大型图像模型的 CNN 内核的最新内容
一、说明 由于OpenAI的ChatGPT的巨大成功引发了大语言模型的繁荣,许多人预见到大图像模型的下一个突破。在这个领域,可以提示视觉模型分析甚至生成图像和视频,其方式类似于我们目前提示 ChatGPT 的方式。 用于大型图像模型的最新深度学习方法…...

索尼电视怎么完全关机
索尼电视怎么完全关机 当用户想要关闭索尼电视时,可能会遇到一些问题。例如,他们可能会遇到如何完全关闭电视的问题。在本文中,我们将介绍如何完全关闭索尼电视。 首先,您需要找到索尼电视的电源按钮。通常,该按钮位…...
AI介绍——chat gpt/文心一言/claude/bard/星火大模型/bing AI
AI体验 1. AI 介绍(注册和使用)1.1 Chat GPT1.2 文心一言1.3 Slack 上的 Claude1.3.1 Claude 介绍1.3.2 Claude 使用 1.4 Google的Bard1.4.1 Bard 介绍1.4.2 Bard 使用 1.5 科大讯飞的星火大模型1.5.1 星火大模型 介绍1.5.2 星火大模型 使用 1.6 new bin…...
C++ 访问控制——公有继承、私有继承、保护继承
派生类继承了基类的全部数据成员和除了构造函数和析构函数之外的全部函数成员,但是这些成员的访问属性在派生的过程中是可以调整的。从基类继承的成员,其访问属性由继承方式控制。 基类的成员有public(公有)、protectedÿ…...

python性能调试
py-spy生成cpu火焰图 ft5.svg env/xxxx/bin pid26443$env/py-spy record -o /tmp/$f --pid $pid --nativememray实时查看内存 env/xxxx/bin$env/python -m memray run --live --trace-python-allocators --native run_demo.pymemray生成内存火焰图报告 frun_demo_042.bin en…...

738. 单调递增的数字
738. 单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10 输出: 9示例 2: 输入: n 1234 输出…...

ssh安全远程管理
目录 1、什么是ssh 2、ssh登陆 3、ssh文件传输 1、什么是ssh ssh是 Secure Shell 的缩写,是一个建立在应用层上的安全远程管理协议。ssh 是目前较为可靠的传输协议,专为远程登录会话和其他网络服务提供安全性。利用ssh 协议可以有效防止远程管理过程中…...
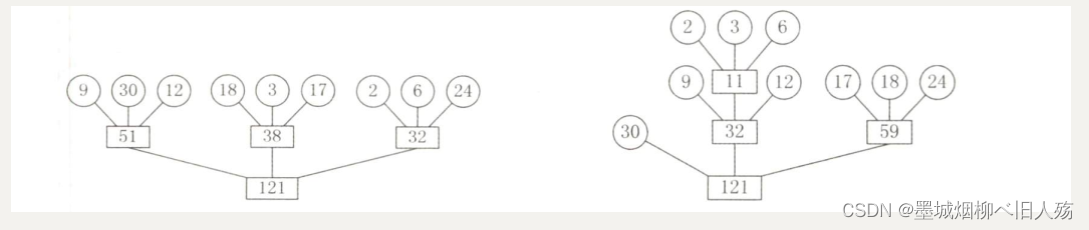
外部排序算法总结
一.内排总结 在之前博客里,博主已经介绍了各种内部排序算法的原理和C语言代码实现,不懂的朋友可以在同系列专栏里选择查看,今天介绍常见排序算法的最后一点,也就是外部排序。在此之前,我们先对外部排序的各种算法做一…...
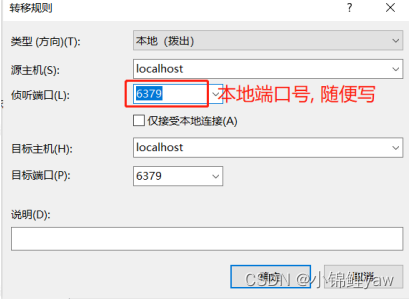
Redis安装以及配置隧道连接(centOs)
目录 1.centOs安装Redis 2. Redis 启动和停⽌ 3. 操作Redis 2.Xshell配置隧道 1.centOs安装Redis #使⽤yum安装Redis yum -y install redis 2. Redis 启动和停⽌ #查看是否启动 ps -ef|grep redis#启动redis: redis-server /etc/redis.conf &#停⽌Redis redis-cli sh…...

mysql二进制方式升级8.0.34
一、概述 mysql8.0.33 存在如下高危漏洞,需要通过升级版本修复漏洞 Oracle MySQL Cluster 安全漏洞(CVE-2023-0361) mysql/8.0.33 Apache Skywalking <8.3 SQL注入漏洞 二、查看mysql版本及安装包信息 [rootlocalhost mysql]# mysql -V mysql Ver 8.0.33 fo…...

Kotlin单例代码实例
目录 一、饿汉式的实现二、懒汉式的实现三、安全 懒汉式的实现四、双重校验DCL 的实现 一、饿汉式的实现 Kotlin版本 object SingletonDemoKt/*** 背后的逻辑代码:public final class SingletonDemoKt {public static final SingletonDemoKt INSTANCE;private Si…...

(7.28-8.3)【大数据新闻速递】《数字孪生工业软件白皮书》、《中国绿色算力发展研究报告》发布;华为ChatGPT要来了
【数字孪生工业软件白皮书(2023)】 近日,第七届数字孪生与智能制造服务学术会议成功举行,2023《数字孪生工业软件白皮书》在会上正式发布。《白皮书》在《Digital Twin》国际期刊专家顾问委员会指导下,由国家重点研发计…...

TikTok海外抖音云控抢金币宝箱
TikTok海外抖音云控抢金币宝箱 中芯密科云控系统是一个稳定、操作简单的自动化管理工具,专为大型机房设计,可以监控、控制和管理机房内的设备。该系统具有负载均衡、操作简单、高容错等特点,能够提高机房设备的稳定性和可用性。 该系统具有以…...

H3C交换机如何通过MAC和IP查寻对应ARP信息
环境: H3C S6520-26Q-SI version 7.1.070, Release 6326 问题描述: H3C交换机如何通过MAC 查寻对应IP信息 解决方案: 一、已知设备MAC地址为ac11-b134-d066 通过MAC 查寻对应IP信息 命令 dis arp | in X-X-X [H3C]dis arp | in ac11…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
