机器学习深度学习——数值稳定性和模型化参数(详细数学推导)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——Dropout
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
这一部分包括了很多概率论和数学的知识,而书上的推导很少,这边会做个比较细致的讨论,数学基础不行就去补,不能拖,深入浅出的感觉是最让人感到心情愉悦的。
数值稳定性和模型初始化
- 梯度消失和梯度爆炸
- 梯度消失
- 梯度爆炸
- 让训练更加稳定
- 参数初始化
- 讨论(各种概率论思维推导)
- 默认初始化
- Xavier初始化
梯度消失和梯度爆炸
一个具有L层、输入x和输出o的深层网络。每一层l由f定义,变换的参数权重为W(l),其隐藏变量为h(l)(令h(0)=x)。则我们的网络可以定义为:
h ( l ) = f l ( h ( l − 1 ) ) 因此 o = f L ○ . . . ○ f 1 ( x ) h^{(l)}=f_l(h^{(l-1)})因此o=f_L○...○f_1(x) h(l)=fl(h(l−1))因此o=fL○...○f1(x)
若所有隐藏向量和输入都是向量,我们可以将o关于任何一组参数W{(l)}的梯度写为:
∂ h ( L − 1 ) h ( L ) ⋅ . . . ⋅ ∂ h ( l ) h ( l + 1 ) ∂ w ( l ) h ( l ) \partial_h(L-1)h^{(L)}·...·\partial_h(l)h^{(l+1)}\partial_w(l)h^{(l)} ∂h(L−1)h(L)⋅...⋅∂h(l)h(l+1)∂w(l)h(l)
换言之,该梯度是一个L-l个矩阵M(L)·…·M(l+1)与梯度向量v{l}的乘积。
这么多的乘积放在一起会出现严重的问题:可能会造成梯度的不稳定。要么是梯度爆炸:参数更新过大,破坏了模型的稳定收敛;要么是梯度消失:参数更新过小,在每次更新时几乎不会移动,导致模型无法学习。
梯度消失
sigmoid就是一个造成梯度消失的常见原因,我们可以绘制sigmoid函数以及它的导数函数观察:
import torch
from d2l import torch as d2lx = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.sigmoid(x)
y.backward(gradient=torch.ones_like(x)) # 参与的参数是非标量的时候,就需要指定gradient为和x形状相同的全1向量(矩阵)d2l.plot(x.detach().numpy(), [y.detach().numpy(), x.grad.numpy()],legend=['sigmoid', 'gradient'], figsize=(4.5, 2.5))
d2l.plt.show()
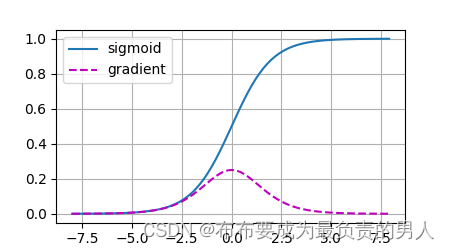
如上图,当sigmoid函数的输入很大或者很小时梯度会消失。此外,当反向传播通过许多层时,除非函数的输入接近于0,否则整个成绩的梯度都可能会消失。因此,更稳定的ReLU系列函数已经成为从业者的默认选择(虽然在神经科学的角度看起来不太合理)。
梯度爆炸
梯度爆炸可能同样令人烦恼。 为了更好地说明这一点,我们生成100个高斯随机矩阵,并将它们与某个初始矩阵相乘。 对于我们选择的尺度(方差σ2=1),矩阵乘积发生爆炸。当这种情况是由于深度网络的初始化所导致时,我们没有机会让梯度下降优化器收敛。
import torchM = torch.normal(0, 1, size=(4, 4))
print('一个矩阵\n', M)
for i in range(100):M = torch.mm(M, torch.normal(0, 1, size=(4, 4)))print('乘以100个矩阵后\n', M)
一个矩阵
tensor([[ 2.2266, 0.1844, -0.1071, -0.7712],
[-0.1580, -0.3028, -0.9375, -0.2922],
[ 0.0616, -1.1593, 1.8516, 1.6285],
[ 0.2703, -0.5483, -0.6187, -1.2804]])
乘以100个矩阵后
tensor([[ 1.3260e+25, -6.2655e+25, 1.2841e+25, 1.5429e+25],
[ 1.5770e+24, -7.4518e+24, 1.5273e+24, 1.8351e+24],
[ 8.5330e+23, -4.0321e+24, 8.2638e+23, 9.9294e+23],
[ 5.7656e+24, -2.7244e+25, 5.5837e+24, 6.7091e+24]])
让训练更加稳定
而如何让我们的训练更加稳定呢?也就是要避免掉梯度消失和梯度爆炸问题。
目标:让梯度值在合理范围内,如[1e-6,1e3]
将乘法变加法:ResNet,LSTM
归一化:梯度归一化,梯度裁剪
合理的权重和激活函数(这是我们的重点)
参数初始化
减轻上面问题的一种方法就是进行参数初始化,优化期间的注意以及适当的正则化也可以使得训练更加的稳定。
讨论(各种概率论思维推导)
我们现在做一个假设:
(1)假设w都是独立同分布的,那么:
E [ w i , j t ] = 0 , D [ w i , j t ] = γ t 2 E[w_{i,j}^t]=0,D[w_{i,j}^t]=γ_t^2 E[wi,jt]=0,D[wi,jt]=γt2
(2)ht-1独立于wt(也就是层的权重与输入是无关的)
我们大胆假设此时没有激活函数,那么
h t = W t h t − 1 ,这里 W t ∈ R n t × n t − 1 h^t=W^th^{t-1},这里W^t∈R^{n_t×n_{t-1}} ht=Wtht−1,这里Wt∈Rnt×nt−1
则容易推出:
E [ h i t ] = E [ ∑ j w i , j t h j t − 1 ] = ∑ j E [ w i , j ] E [ h j t − 1 ] = 0 (独立同分布的推广) E[h_i^t]=E[\sum_jw_{i,j}^th_j^{t-1}]=\sum_jE[w_{i,j}]E[h_j^{t-1}]=0(独立同分布的推广) E[hit]=E[j∑wi,jthjt−1]=j∑E[wi,j]E[hjt−1]=0(独立同分布的推广)
此时我们分别计算正向方差与反向方差,并且让他们都相同。
正向方差
D [ h i t ] = E [ ( h i t ) 2 ] − E [ h i t ] 2 = E [ ( ∑ j w i , j t h j t − 1 ) 2 ] (前面假设过独立同分布那么 E [ h i t ] = 0 ) = E [ ∑ j ( w i , j t ) 2 ( h j t − 1 ) 2 + ∑ j ≠ k w i , j t w i , k t h j t − 1 h k t − 1 ] (这里就是 ( a + b + c + . . . ) 2 的计算方式) 由于独立同分布,所以 ∑ j ≠ k w i , j t w i , k t h j t − 1 h k t − 1 = 0 ,则 上式 = ∑ j E [ ( w i , j t ) 2 ] E [ ( h j t − 1 ) 2 ] = ∑ j ( E [ ( w i , j t ) 2 ] − E [ w i , j t ] 2 ) ( E [ ( h j t − 1 ) 2 ] − E [ h j t − 1 ] 2 ) (构造出 D ) = ∑ j D [ w i , j t ] D [ h j t − 1 ] = n t − 1 γ t 2 D [ h j t − 1 ] D[h_i^t]=E[(h_i^t)^2]-E[h_i^t]^2=E[(\sum_jw_{i,j}^th_j^{t-1})^2](前面假设过独立同分布那么E[h_i^t]=0)\\ =E[\sum_j(w_{i,j}^t)^2(h_j^{t-1})^2+\sum_{j≠k}w_{i,j}^tw_{i,k}^th_j^{t-1}h_k^{t-1}](这里就是(a+b+c+...)^2的计算方式)\\ 由于独立同分布,所以\sum_{j≠k}w_{i,j}^tw_{i,k}^th_j^{t-1}h_k^{t-1}=0,则\\ 上式=\sum_jE[(w_{i,j}^t)^2]E[(h_j^{t-1})^2]\\ =\sum_j(E[(w_{i,j}^t)^2]-E[w_{i,j}^t]^2)(E[(h_j^{t-1})^2]-E[h_j^{t-1}]^2)(构造出D)\\ =\sum_jD[w_{i,j}^t]D[h_j^{t-1}]=n_{t-1}γ_t^2D[h_j^{t-1}] D[hit]=E[(hit)2]−E[hit]2=E[(j∑wi,jthjt−1)2](前面假设过独立同分布那么E[hit]=0)=E[j∑(wi,jt)2(hjt−1)2+j=k∑wi,jtwi,kthjt−1hkt−1](这里就是(a+b+c+...)2的计算方式)由于独立同分布,所以j=k∑wi,jtwi,kthjt−1hkt−1=0,则上式=j∑E[(wi,jt)2]E[(hjt−1)2]=j∑(E[(wi,jt)2]−E[wi,jt]2)(E[(hjt−1)2]−E[hjt−1]2)(构造出D)=j∑D[wi,jt]D[hjt−1]=nt−1γt2D[hjt−1]
我们让t层输入的反差与输出的方差都是相同的,那么可以推出:
n t − 1 γ t 2 = 1 (其中 n t − 1 代表第 t 层输入的规模) n_{t-1}γ_t^2=1(其中n_{t-1}代表第t层输入的规模) nt−1γt2=1(其中nt−1代表第t层输入的规模)
其他层也是同理的。
反向方差
而反向和正向的情况就类似了,可以这么推导:
∂ l ∂ h t − 1 = ∂ l ∂ h t W t \frac{\partial l}{\partial h^{t-1}}=\frac{\partial l}{\partial h^t}W^t ∂ht−1∂l=∂ht∂lWt
分别取转置,得:
( ∂ l ∂ h t − 1 ) T = ( W t ) T ( ∂ l ∂ h t ) T (\frac{\partial l}{\partial h^{t-1}})^T=(W^t)^T(\frac{\partial l}{\partial h^t})^T (∂ht−1∂l)T=(Wt)T(∂ht∂l)T
依旧假设:
E [ ∂ l ∂ h i t − 1 ] = 0 E[\frac{\partial l}{\partial h_i^{t-1}}]=0 E[∂hit−1∂l]=0
则
D [ ∂ l ∂ h i t − 1 ] = n t γ t 2 D [ ∂ l ∂ h j t ] D[\frac{\partial l}{\partial h_i^{t-1}}]=n_tγ_t^2D[\frac{\partial l}{\partial h_j^t}] D[∂hit−1∂l]=ntγt2D[∂hjt∂l]
这时我们可以推出:
n t γ t 2 = 1 (其中 n t 代表第 t 层输出的规模) n_tγ_t^2=1(其中n_t代表第t层输出的规模) ntγt2=1(其中nt代表第t层输出的规模)
其他层也是同理的。
照着上面的方式推下去,我们最终整合起来的结论是
n t − 1 γ t 2 = 1 和 n t γ t 2 = 1 n_{t-1}γ_t^2=1和n_tγ_t^2=1 nt−1γt2=1和ntγt2=1
显然我们要满足上面的式子,当且仅当:
n t − 1 = n t n_{t-1}=n_t nt−1=nt
这并不容易满足,因为我们很难说对于一层中,我们的输入和输出的规模(神经元的数量)是相同的。
接下来就会谈到Xavier初始化,将会用另外一种方式来解决这一问题。
默认初始化
在前面的学习中,我们初始化权重值的方式都是使用正态分布来。而如果我们不指定初始化方法的话,框架会使用默认的随机初始化方法(比如Linear就会提供,具体原理可以自行去了解),简单问题用默认初始化还是很有效的。
Xavier初始化
回到之前的讨论,我们已知很难同时满足
n t − 1 γ t 2 = n t γ t 2 = 1 n_{t-1}γ_t^2=n_tγ_t^2=1 nt−1γt2=ntγt2=1
我们推广到每一层,即为:
n i n σ 2 = n o u t σ 2 = 1 n_{in}\sigma^2=n_{out}\sigma^2=1 ninσ2=noutσ2=1
虽然难以满足输入和输出规模相同,但是我们可以先将两个式子相加并调整:
σ 2 ( n i n + n o u t ) / 2 = 1 → σ = 2 ( n i n + n o u t ) \sigma^2(n_{in}+n_{out})/2=1→\sigma=\sqrt\frac{2}{(n_{in}+n_{out})} σ2(nin+nout)/2=1→σ=(nin+nout)2
对于上面的式子,我们就可以有两种采样方式:
(1)Xavier初始化从均值为0,方差为
σ 2 = 2 n i n + n o u t \sigma^2=\frac{2}{n_{in}+n_{out}} σ2=nin+nout2
的高斯分布中采样权重,即为
正态分布 N ( 0 , 2 n i n + n o u t ) 正态分布N(0,\sqrt\frac{2}{n_{in}+n_{out}}) 正态分布N(0,nin+nout2)
(2)从均匀分布从抽取权重时的方差,我们先注意一个定理:
均匀分布 U ( − a , a ) 的方差为 a 2 3 均匀分布U(-a,a)的方差为\frac{a^2}{3} 均匀分布U(−a,a)的方差为3a2
此时我们将其带入到σ2的条件中,将得到初始化值域:
均匀分布 U ( − 6 n i n + n o u t , 6 n i n + n o u t ) 均匀分布U(-\sqrt\frac{6}{n_{in}+n_{out}},\sqrt\frac{6}{n_{in}+n_{out}}) 均匀分布U(−nin+nout6,nin+nout6)
相关文章:

机器学习深度学习——数值稳定性和模型化参数(详细数学推导)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——Dropout 📚订阅专栏:机器学习&&深度学习 希望文章对你们有所帮助 这一部…...

layui 整合UEditor 百度编辑器
layui 整合UEditor 百度编辑器 第一步:下载百度编辑器并配置好路径 百度编辑器下载地址:http://fex.baidu.com/ueditor/ 第二步:引入百度编辑器 代码如下: <div class"layui-form-item layui-form-text"><…...
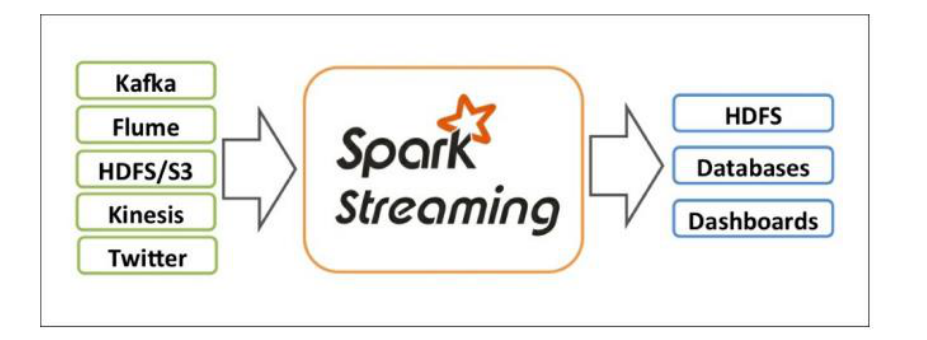
1、sparkStreaming概述
1、sparkStreaming概述 1.1 SparkStreaming是什么 它是一个可扩展,高吞吐具有容错性的流式计算框架 吞吐量:单位时间内成功传输数据的数量 之前我们接触的spark-core和spark-sql都是处理属于离线批处理任务,数据一般都是在固定位置上&…...
【Spring Boot】Spring Boot 集成 RocketMQ 实现简单的消息发送和消费
文章目录 前言基本概念消息和主题相关发送普通消息 发送顺序消息RocketMQTemplate的API介绍参考资料: 前言 本文主要有以下内容: 简单消息的发送顺序消息的发送RocketMQTemplate的API介绍 环境搭建: RocketMQ的安装教程:在官网…...

uniapp:图片验证码检验问题处理
图形验证码功能实现 uniapp:解决图形验证码问题及利用arraybuffer二进制转base64格式图片(后端传的图片数据形式:x00\x10JFIF\x00\x01\x02\x00…)_❆VE❆的博客-CSDN博客 UI稿: 需求:向后端请求验证码图片&…...
将Visio和Excel导出成没有白边的PDF文件
1、VISIO如何无白边导出pdf格式 在使用Latex时,要导入矢量图eps格式。但是VISIO无法输出eps格式,这就需要将其导出为pdf。但是导出pdf时,往往会有大量的白边。VISIO无白边导出pdf格式的方法如下: 1.文件——开发工具——显示sha…...
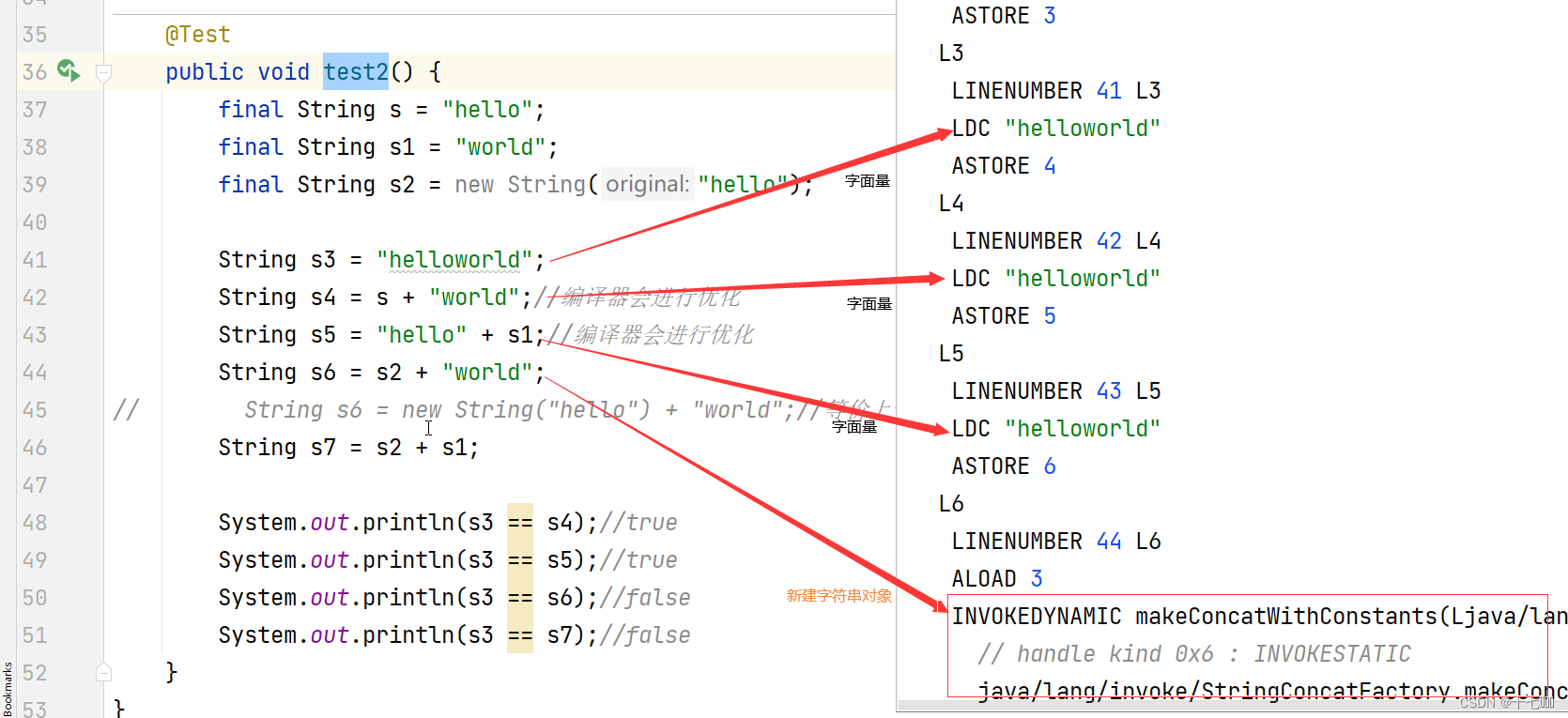
String类及其工具类
一、String类 1.字符串对象 String str new String("hello");String对象是final修饰的,不可修改的,修改后的字符串对象是另外一个对象,只是修改了引用地址。每次创建都会创建一个新的对象。 2. 字面量 String s "hello&…...
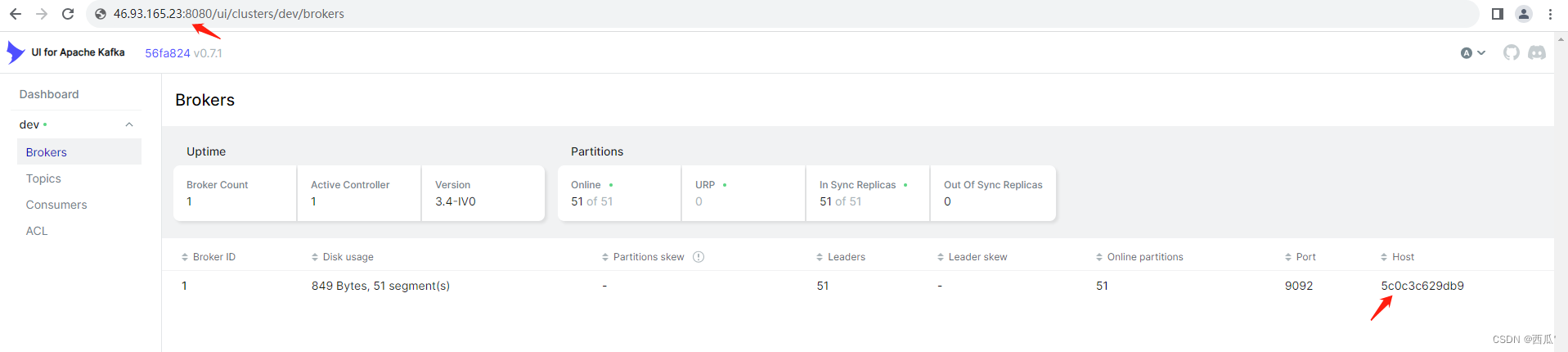
踩坑(5)整合kafka 报错 java.net.UnknownHostException: 不知道这样的主机
java.net.UnknownHostException: 不知道这样的主机。 (5c0c3c629db9)at java.base/java.net.Inet6AddressImpl.lookupAllHostAddr(Native Method) ~[na:na]at java.base/java.net.InetAddress$PlatformNameService.lookupAllHostAddr(InetAddress.java:933) ~[na:na]at java.ba…...

rust持续学习 get_or_insert_with
通常使用一个值 if(xnull)xsome_valid_value 忽然今天看见一段代码 pub fn get_id() -> u64 { let mut res struct.data.borrow_mut(); *res.get_or_insert_with(||{let mut xx ...... some logiclet id xx.id; id}); }感觉这个名字蛮奇怪的 insert 然后翻了一下代码&a…...
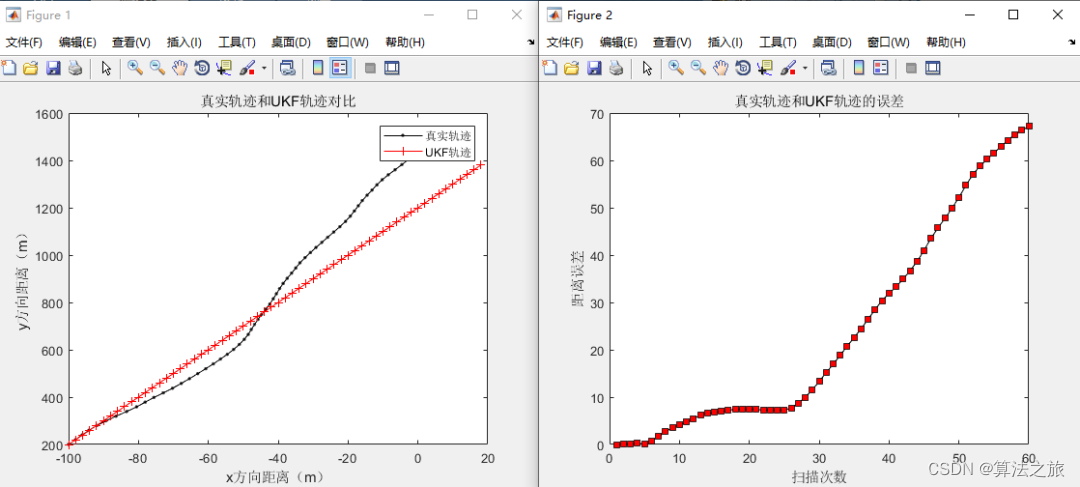
卡尔曼滤波 | Matlab实现无迹kalman滤波仿真
文章目录 效果一览文章概述研究内容程序设计参考资料效果一览 文章概述 卡尔曼滤波 | Matlab实现无迹kalman滤波仿真 研究内容 无迹kalman滤波(UKF)不是采用的将非线性函数线性化的做法。无迹kalman仍然采用的是线性kalman滤波的架构,对于一步预测方程,使用无迹变换(UT)来…...
C++---list常用接口和模拟实现
list---模拟实现 list的简介list函数的使用构造函数迭代器的使用list的capacitylist element accesslist modifiers list的模拟实现构造函数,拷贝构造函数和迭代器begin和endinsert和eraseclear和析构函数 源码 list的简介 list是用双向带头联表实现的一个容器&…...

[openCV]基于赛道追踪的智能车巡线方案V1
import cv2 as cv import os import numpy as npimport time# 遍历文件夹函数 def getFileList(dir, Filelist, extNone):"""获取文件夹及其子文件夹中文件列表输入 dir:文件夹根目录输入 ext: 扩展名返回: 文件路径列表""&quo…...
SpringIoc-个人学习笔记
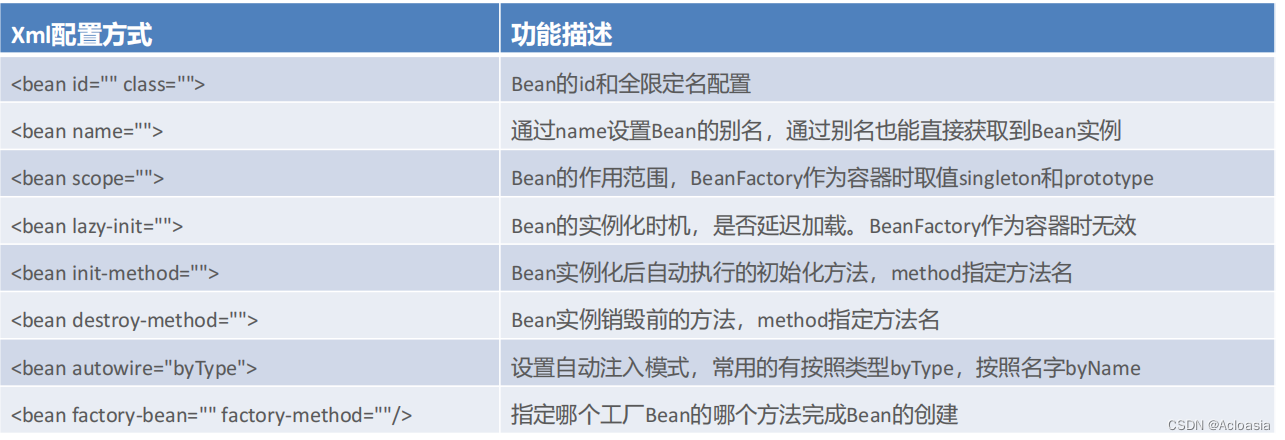
Spring的Ioc、DI、AOP思想 Ioc Ioc思想:Inversion of Control,控制反转,在创建Bean的权利反转给第三方 DI DI思想:Dependency Injection,依赖注入,强调Bean之间的关系,这种关系由第三方负责去设…...

【一文搞懂泛型】
3.3泛型 3.3.1泛型出现的背景 泛型出现的背景有两点: 第一点是在集合容器中,如果没有指定对应类型的话,那么底层的元素就是object,要对容器中的元素进行存取的时候,取出来的同时需要进行类型转换,如果有…...

概念解析 | 利用MIMO雷达技术实现高性能目标检测的关键技术解析
注1:本文系“概念解析”系列之一,致力于简洁清晰地解释、辨析复杂而专业的概念。本次辨析的概念是:MIMO雷达目标检测技术 参考资料:何子述, 程子扬, 李军, 等. 集中式 MIMO 雷达研究综述[J]. 雷达学报, 2022, 11(5): 805-829. 利用MIMO雷达技术实现高性能目标检测的关键技术解…...
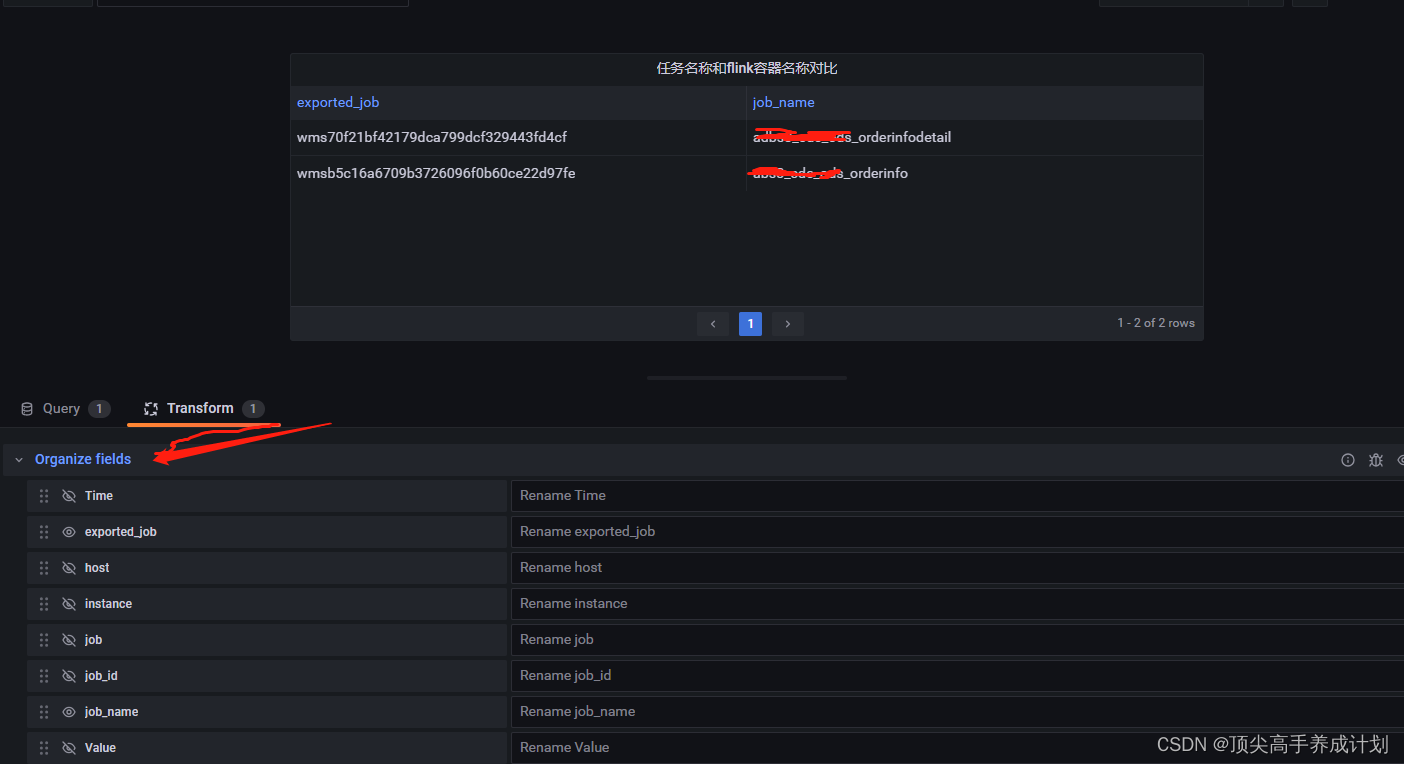
Grafana制作图表-自定义Flink监控图表
简要 有时候我们在官网的Grafana下载的图表是这样的,如下图 #算子的处理时间,就是处理数据的延迟数据抓取,这个的说明看下下面的文章 metrics.latency.interval: 60 metrics.reporter.promgateway.class: org.apache.flink.metrics.prometh…...
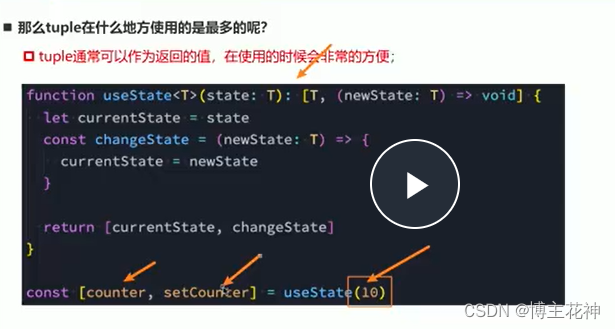
【TypeScript】初识TypeScript和变量类型介绍
TypeScript 1,TypeScript是什么?2,类型的缺失带来的影响3,Ts搭建环境-本博主有专门的文章专说明这个4,使用tsc对ts文件进行编译5,TS运行初体验简化Ts运行步骤解决方案1解决方案2(常见) 开始学习…...
阿里云瑶池 PolarDB 开源官网焕新升级上线
导读近日,阿里云开源云原生数据库 PolarDB 官方网站全新升级上线。作为 PolarDB 开源项目与开发者、生态伙伴、用户沟通的平台,将以开放、共享、促进交流为宗旨,打造开放多元的环境,以实现共享共赢的目标。 立即体验全新官网&…...

泡水书为什么不能再出售
近日,京津冀持续强降雨,多家出版机构位于涿州等地的图书库房受到影响。 中图网11日发文称,其位于涿州的仓储中心被洪水淹了,一库房有400多万册的书籍。 网友纷纷在文章下暖心留言:注意人身安全,泡水的书也…...

Mac 执行 .sh命令报错 command not found
使用终端执行.sh命令,可输入: ./FileName.sh如果提示 Permission denied 权限不足,可增加sudo,命令如下: sudo ./FileName.sh如果提示 command not found 可以这样: chmod ux *.sh sudo ./FileName.sh...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
